Existence of solution to a class of fractional delay differential equation under multi-points boundary conditions

Abstract

In this manuscript, a class of fractional delay differential equation is considered under multi-point boundary conditions. Two important aspects including existence theory and stability results are developed. For the concerned results prior estimate method and some results of nonlinear analysis are used. By giving a pertinent example the main results are justified.

Keywords:

• Delay differential equation
• multi-points boundary value problem
• topological degree theory

1. Introduction

The theory of fractional differential equations (FDEs) is one of the fastest-growing area of research in recent time and the mentioned equations have many applications in engineering and scientific discipline such as chemistry, control theory, physics, economics, signal processing, biology, optimization theory, etc, we refer to (Hilfer, 2000; Kilbas, Marichev, & Samko, 1993, Kilbas, Srivastava, & Trujillo, 2006; Miller & Ross, 1993; Podlubny, 1999). The existence and uniqueness of solution to BVPs are well studied for the FDEs, we refer the readers to (Agarwal, Benchohra, & Hamani, 2010; Ahmad & Nieto, 2010; Benchohra, Graef, & Hamani, 2008; Li, Luo, & Zhou, 2010). Further multi-point BVPs have been analyzed for the existence and uniqueness of solution through fixed point theory in detail (see Cui, Yu, & Mao, 2012; El-Sayed & Bin-Taher, 2013; El-Shahed & Nieto, 2010; Khan, 2013; Rehman & Khan, 2010; Zhong & Lin, 2010 and in the references therein). Delay differential equations constitute a large class of the concerned area. Such type of equations include continuous, discrete and proportional type delay terms. The respective equations have significant applications in mathematical modeling of various process and phenomenons. In this regards recently significant developments has been made by various authors to investigate various problems. In this concerned investigations authors have established some numerical and analytical investigations to various initial and BVPs which are modeling real world problems (for detail see Ahmad & Khan, 2019, 2020; Ahmad, Khan, & Cesarano, 2019; Ahmad, Khan, & Yao, 2020; Ahmad, Seadawy, & Khan, 2020a, 2020b; Ahmad, Seadawy, Khan, & Thounthong, 2020). Among delay differential equations, pantograph is that class which includes proportional type delay term. The pantograph equations have many applications in various fields like electrodynamics, astrophysics, non-linear dynamical system, quantum mechanics, cell growth and probability theory on algebraic structures (Rahimkhani, Ordokhani, & Babolian, 2017; Saeed & Ur Rehman, 2014; Yang & Huang, 2013). Further, FDEs provides greater degree of freedom in the description of many biological and physical problem. For instance a simple population decay problem with given initial value (1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) has exact solution $$\omega (t)={10}^6{E}_q(-t^q).$$

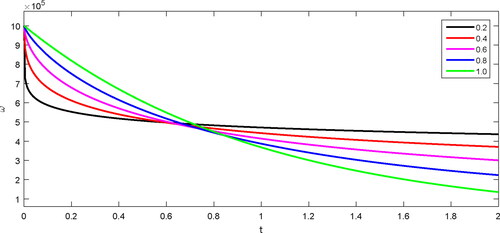
From Figure 1, we see that smaller the fractional order faster the decay process and rapidly the stability result occurs and vice versa.

Figure 1. Graphical presentation for different values of q.

The nonlocal BVPs of FDEs have several applications in various disciplines of engineering and sciences including hydromechanics, dynamics. The qualitative theory of multi-point BVPs has become an active area of research in the last two decades. By using different tools of fixed point theory and functional analysis, the concerned area has been very well-studied (Abbas, 2015; Ahmad & Nieto, 2009; Shah & Khan, 2016; Shah, Zeb, & Khan, 2015). However, in the stated papers, the conditions for the existence and uniqueness of solution need compactness of the operators which is a strong condition. To relax the condition of being compact, the researchers used the topological degree theory. In this regard, Mawhin (Mawhin, 1979) used topological degree theory for the solution of classical DEs. Isaia has extended the results for the uniqueness and existence of solution to non-linear integral equation by using topological degree theory (Isaia, 2006). In 2013, Wang, Zhou, and Wei (2012) studied the nonlocal Cauchy problem via topological degree theory and later on the method was extended for multi-point FDEs (see Khan & Shah, 2015; Kumam, Ali, Shah, & Khan, 2017). Further, in recent times some authors have investigated symmetry of FDEs for various problems. The mentioned tools provide a systemic procedure for dealing the aforesaid area very well, for detail see Wang, Liu, & Zhang, 2013, Wang, Kara, & Fakhar, 2015; Wang & Kara, 2018, 2019; Wang, Liu, Wu, & Su, 2020; Wang, Vega-Guzman, Biswas, Alzahrani, & Kara, 2020; Wang, Yang, Gu, Guan, & Kara, 2020.

Motivated from the above-discussed work, we studied the delay FDEs with nonlocal multi-point boundary condition for the existence and uniqueness of solution in the following form (2) $$\{\begin{array}{l}{}_0^C{D}_t^q\omega (t)+f(t,\omega (t),\omega (\mu t))=0, n-1<q\le n,\hspace{1em}0<\mu <1, t\in \mathsf{J}\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(i)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)+\mathsf{h}(\omega ),\hspace{1em}i=1,2,\dots ,n-2,\end{array}$$(2) where ${}_0^C{D}_t^q$ is the standard Caputo’s derivative of order q, $\mathsf{J}=[0, 1]$ and ${\delta }_i,{\eta }_i\in (0,1)$ with ${\sum }_{i=1}^{m-2}{\delta }_i{\eta }_i^{q-1}<1,$ the non-linear function $f:\mathsf{J}\times {\mathcal{R}}^2\to \mathcal{R}$ is continuous and $\mathsf{g}(\omega ), \mathsf{h}(\omega ):[0, 1]\to \mathcal{R}$ are continuous functions.

Another important perspective of qualitative theory is stability analysis for DEs which is very important for optimization and numerical point of view. Stability analysis is a prominent aspects of applied analysis which needs investigations during dealing with many problems. For the stability, various concepts have been developed in literature in past including Lyapunov, Mittag-Leffler and Ulam-Hyers stabilities. These stabilities were well studied for differential and integral equations. The Ulam-Hyers type stability was initiated, when Ulam (1964) put a question that “Under what conditions does there exists an additive mapping near an approximately additive mapping?”. In has response, Hyer (Aoki, 1950; Hyers, 1941) answered Ulam’s question for the additive mapping in complete norm spaces. This turn to the new area of stability which is known as Ulam-Hyers stability. Further, the Ulam-Hyers stability has been generalized by Rassias and also the said scheme was greatly developed for many kinds of problems devoted to ordinary as well as FDEs (see Ameen, Jarad, & Abdeljawad, 2018; Jung, 2004; Ulam, 1960; Wang, Lv, & Zhou, 2011) and the references therein). As we know the mentioned stability and its various form have been vary rarely studied for delay FDEs especially for multi-point BVPs. Therefore, we will discuss the various type of stabilities, including “Ulam-Hyers (UH), generalized Ulam-Hyers (GUH), Ulam-Hayers-Rassies (UHR) and generalized Ulam-Hyers-Rassies (GUHR)” stabilities for the considered problem. Further, an example is given to illustrate the main results.

Organization of the manuscript: This work is organized as in Section 1 a detailed introduction is provided. In Section 2, some necessary background materials are recalled. Further in Section 3, main results and in Section 4 stability results are given. In Section 5 some test problems are provided. Last Section 6 is devoted to a brief conclusion.

2. Preliminaries

The concern section is committed to definition, preliminary facts and notations which are used through out this paper. We define the Banach space $\mathsf{X}=C[0, 1]$ under the norm given by $\left|\right|\omega \left|\right|=\underset{t\in \mathsf{J}}{\max }|\omega (t)|.$

Definition 1

(Kilbas et al., 2006). The integral for non-integer order q > 0 of the function f is given below $${}_0{I}_t^{q}f(t)=\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ) d\zeta .$$

Definition 2

(Kilbas et al., 2006). Derivative of non-integer order q > 0 for the function f in sense of Caputo is define as $${}_0^C{D}_t^{q}f(t)=\frac{1}{\Gamma (n-q)}{\int }_0^t{(t-\zeta )}^{n-q-1}{f}^{(n)}(\zeta )d\zeta ,$$ such that $n=[q]+1,$ and right hand side is defined on ${\mathcal{R}}^{+},$ pointwise.

Lemma 1

(Kilbas et al., 2006). Let $\omega \in L(0,1)\cap C(0,1)$, the FDEs with order q > 0 $${}_0^C{D}_t^q\omega (t)=0,$$ has a solution in the form $$\omega (t)=c_0+c_{1}t+\dots +c_{n-1}{t}^{n-1},\hspace{1em}\mathsf{ }{c}_i\in \mathcal{R},\hspace{1em}\mathsf{ }i=0,1,2,\dots ,n-1.$$

Lemma 2

(Kilbas et al., 2006). Consider $\omega \in L(0,1)\cap C(0,1)$, with derivative of non-integer order q > 0, then $${}_0{I}_t^q{[}_0^C{D}_t^q\omega (t)]=\omega (t)+c_0+c_{1}t+\dots +c_{n-1}{t}^{n-1},\hspace{1em}\mathsf{ }{c}_i\in \mathcal{R},\hspace{1em}\mathsf{ }i=0,1,2,\dots ,n-1.$$

Definition 3.

The Kuratwoski measure of non-compactness $\beta :\mathsf{A}\to {\mathcal{R}}_{+}$ is define as $$\beta (A)=\inf \{\mathsf{ }d>0\},$$ where $A\in \mathsf{A}$ is finite cover by sets of diameter ≤d.

Definition 4

(Rakočević, 1998). A continuous bounded function $\mathsf{F}:\mathsf{X}\to \mathsf{X}$ is said to be β-contraction if there exist a positive constant K such that for all bounded subset B of X: $$\beta (\mathsf{F}(B)) \le K\beta (B).$$

Further, if K < 0, then F is strick β-contraction and is called β-condensing if K = 1.

Proposition 1

(Deimling, 1985). If $\mathsf{F}, \mathsf{G}:\mathsf{X}\to \mathsf{X}$ are β-contraction with constant K and $K\prime$, then $\mathsf{F}+\mathsf{G}:\mathsf{X}\to \mathsf{X}$ is β-contraction with constant $K+K\prime .$

Proposition 2

(Deimling, 1985). If $\mathsf{F}:\mathsf{X}\to \mathsf{X}$ is compact, then $\mathsf{F}$ is β-contraction with constant K = 0.

Proposition 3

(Deimling, 1985). If $\mathsf{F}:\mathsf{X}\to \mathsf{X}$ is contraction with constant K, then $\mathsf{F}$ is β-contraction with the same constant K.

Theorem 1

(Isaia, 2006). Let $\mathsf{F}:\mathsf{X}\to \mathsf{X}$ be β-condensing and $$\Lambda =\{x\in \mathsf{X}:\exists △\in [0,1] \mathit{such} \mathit{that} x=△\mathsf{F}x\}.$$

If Λ is a bounded set in X, so there exist r > 0 such that $\Lambda \subset B_r(0),$ then the degree $$D(I-△\mathsf{F},B_r(0),0)=1.$$

Consequently, F has at least one fixed point and the set of fixed points of F lies in B_r(0)

3. Main results

In this portion, we provide some of main results about the problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ).

Lemma 3.

Let $\alpha :\mathsf{J}\to \mathcal{R}$ be contiguous function, then the BVP (3) $$\begin{array}{l}{}_0^C{D}_t^q\omega (t)+\alpha (t)=0, n-1<q\le n,\hspace{1em}0<t,\mu <1\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(i)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)\\ +\mathsf{h}(\omega )\hspace{1em}i=1,2,\dots ,n-2,\end{array}$$(3) has at most one solution given by $$\begin{array}{c}\omega (t)=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega )+\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}\alpha (\zeta )d\zeta \\ -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\alpha (\zeta )d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\alpha (\zeta )d\zeta .\end{array}$$

Proof.

Applying ${}_0{I}^q$ to above BVP (3) and using Lemma 2, we have (4) $$\omega (t)=-\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\alpha (\zeta )d\zeta -c_0-c_{1}t-\dots -c_{n-1}{t}^{n-1}.$$(4)

Now the condition $\omega (0)=\mathsf{g}(\omega )$ and ${\omega }^{(i)}(0)=0 \mathit{for}, i=1,2,\dots ,n-2$ yields $c_0=-\mathsf{g}(\omega )$ and $c_1=c_2=\cdots =c_{n-2}=0.$ And the condition $\omega (1)={\sum }_{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)+\mathsf{h}(\omega )$ gives $$c_{n-1}=-[\frac{1}{\lambda }\mathsf{h}(\omega )-\frac{\delta }{\lambda }\mathsf{g}(\omega )+\frac{1}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}\alpha (\zeta )d\zeta -\frac{\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\alpha (\zeta )d\zeta ].$$ where $\lambda =1-{\sum }_{i=1}^{m-2}{\delta }_i{\eta }_i^{n-1}$ and $\delta =1-{\sum }_{i=1}^{m-2}{\delta }_i,$ putting these values in Equation (4)(4) $$\omega (t)=-\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\alpha (\zeta )d\zeta -c_0-c_{1}t-\dots -c_{n-1}{t}^{n-1}.$$(4) , one has $$\begin{array}{c}\omega (t)=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega )+\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}\alpha (\zeta )d\zeta \\ -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\alpha (\zeta )d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\alpha (\zeta )d\zeta .\end{array}$$

□

In view of Lemma 3, the solution of our propose problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is given below (5) $$\begin{array}{c}\omega (t)=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega )+\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta .\end{array}$$(5)

Let suppose $\mathsf{F}, \mathsf{G},\mathsf{T}:\mathsf{X}\to \mathsf{X},$ are operators define as $$\begin{array}{c}\mathsf{F}\omega (t)=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega ),\\ \mathsf{G}\omega (t)=\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta ,\\ \mathsf{T}\omega =\mathsf{F}\omega +\mathsf{G}\omega .\end{array}$$

Since f, g, h are continuous functions, so the operator $\mathsf{T}$ is well defines. And the fixed point of the operator $\mathsf{T}$ means, solution of the propose problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ).

Consider the assumption given below to be hold, for any $\upsilon , \vartheta \in \mathsf{X}$ and $(t, \upsilon , \vartheta )\in \mathsf{J}\times \mathsf{X}.$

$({\mathbf{A}}_1)$ For the constants ${\mathcal{K}}_g, {\mathcal{C}}_g, {\mathcal{M}}_g,p_1\in [0,1)$ the inequality hold $$|\mathsf{g}(\upsilon )-\mathsf{g}(\vartheta )|\le {\mathcal{K}}_g\left|\right|\upsilon -\vartheta \left|\right|,\hspace{1em}|\mathsf{g}(\upsilon )|\le {\mathcal{C}}_g\left|\right|\upsilon |{|}^{p_1}+{\mathcal{M}}_g$$

$({\mathbf{A}}_2)$ For the constants ${\mathcal{K}}_h, {\mathcal{C}}_h, {\mathcal{M}}_h,p_1\in [0,1)$ the inequality hold $$|\mathsf{h}(\upsilon )-\mathsf{h}(\vartheta )|\le {\mathcal{K}}_h\left|\right|\upsilon -\vartheta \left|\right|,\hspace{1em}|\mathsf{h}(\upsilon )|\le {\mathcal{C}}_h\left|\right|\upsilon |{|}^{p_1}+{\mathcal{M}}_h$$

$({\mathbf{A}}_3)$ For the constants ${\mathcal{C}}_f^1, {\mathcal{C}}_f^2, {\mathcal{M}}_f,p_2\in [0,1)$ the inequality hold $$|f(t,\upsilon (t),\vartheta (t)|\le {\mathcal{C}}_f^1|\left|\upsilon \right|{|}^{p_2}+{\mathcal{C}}_f^2\left|\right|\vartheta |{|}^{p_2}+{\mathcal{M}}_f.$$

Lemma 4.

$\mathsf{F}:\mathsf{X}\to \mathsf{X}$ is a contraction operator and satisfy the growth conditions.

Proof.

By applying the assumption $({\mathbf{A}}_1)$ and $({\mathbf{A}}_2),$ we have $$\begin{array}{c}|\mathsf{F}\omega (t)-\mathsf{F}\overline{\omega }(t)|=\left|\right(1-\frac{t^{n-1}\delta }{\lambda }\left)\right[\mathsf{g}(\omega )-\mathsf{g}(\overline{\omega })]+\frac{t^{n-1}}{\lambda }[\mathsf{h}(\omega )-\mathsf{h}(\overline{\omega })\left]\right|\\ \le \left|\left(1-\frac{t^{n-1}\delta }{\lambda }\right)\right|\left|\mathsf{g}(\omega )-\mathsf{g}(\overline{\omega })\right|+\left|\frac{t^{n-1}}{\lambda }\right|\left|\mathsf{h}(\omega )-\mathsf{h}(\overline{\omega })\right|\\ \le \left(\frac{\lambda +1}{\lambda }\right){\mathcal{K}}_g\Vert \omega -\overline{\omega }\left|\right|+\frac{1}{\lambda }{\mathcal{K}}_h\Vert \omega -\overline{\omega }\left|\right|\\ \le {\mathsf{K}}_g\left|\right|\omega -\overline{\omega }\left|\right|+{\mathsf{K}}_h\left|\right|\omega -\overline{\omega }\left|\right|=\mathsf{K}\left|\right|\omega -\overline{\omega }\left|\right|.\end{array}$$ where ${\mathsf{K}}_g=\left(\frac{\lambda +1}{\lambda }\right){\mathcal{K}}_g,{\mathsf{K}}_h=\frac{1}{\lambda }{\mathcal{K}}_h$ and $\mathsf{K}={\mathsf{K}}_g+{\mathsf{K}}_h.$ This shows that F is contraction and hence by Proposition (3(3) $$\begin{array}{l}{}_0^C{D}_t^q\omega (t)+\alpha (t)=0, n-1<q\le n,\hspace{1em}0<t,\mu <1\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(i)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)\\ +\mathsf{h}(\omega )\hspace{1em}i=1,2,\dots ,n-2,\end{array}$$(3) ) is also β-contraction. Also for the growth condition one have (6) $$\left|\right|\mathsf{F}\omega \left|\right|\le {\mathsf{C}}_g\left|\right|\omega |{|}^{p_1}+{\mathsf{C}}_h|\left|\omega \right|{|}^{p_1}.$$(6)

□

Lemma 5.

$\mathsf{G}:\mathsf{X}\to \mathsf{X}$ is a continuous operator and under assumption $({\mathbf{A}}_3)$ satisfy the growth condition $$\left|\right|\mathsf{G}\omega \left|\right|\le \frac{3({\mathsf{C}}_f|\left|\omega \right|{|}^{p_2}+{\mathsf{M}}_f)}{\lambda \Gamma (q+1)},\hspace{1em}\omega \in \mathsf{X}.$$

Proof.

Consider a sequence $\left\{{\omega }_n\right\}$ such that ${\omega }_n\to \omega$ in B_k, where $B_k=\left\{\right|\left|\omega \right||\le \gamma : \omega \in \mathsf{X}\}.$ Now consider $$\begin{array}{c}|\mathsf{G}{\omega }_n(t)-\mathsf{G}\omega (t)|\le \frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}|f(\zeta ,{\omega }_n(\zeta ),{\omega }_n(\mu \zeta ))-f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))|d\zeta +\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}|f(\zeta ,{\omega }_n(\zeta ),{\omega }_n(\mu \zeta ))-f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))|d\zeta \\ +\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}|f(\zeta ,{\omega }_n(\zeta ),{\omega }_n(\mu \zeta ))-f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))|d\zeta .\end{array}$$

Science f is continuous and ${\omega }_n\to \omega as n\to \infty ,$ hence $f(\zeta ,{\omega }_n(\zeta ),{\omega }_n(\mu \zeta ))\to f(\zeta ,\omega (\zeta ),\omega (\mu \zeta )).$ Hence, $\left|\right|\mathsf{G}{\omega }_n(t)-\mathsf{G}\omega (t)\left|\right|$ tends to zero as $n\to \infty .$

Now for the growth condition, one have $$\begin{array}{l}|\mathsf{G}\omega (t)|\le |\frac{t^{n-1}}{\lambda \Gamma (q)}({\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\sum _{i=1}^{m-2}{\delta }_i{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta )|\\ +|\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta |,\\ \le \frac{1}{\lambda \Gamma (q)}\left[{\int }_0^1{(1-\zeta )}^{q-1}\left|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))\right|d\zeta +\sum _{i=1}^{m-2}{\delta }_i{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\left|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \right|\right]\\ +\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\left|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))\right|d\zeta ,\\ \le \frac{2}{\lambda \Gamma (q+1)}(C_f^1|\omega (t){|}^{p_2}+C_f^2|\omega (\mu t){|}^{p_2}+M_f)+\frac{1}{\Gamma (q+1)}(C_f^1|\omega (t){|}^{p_2}+C_f^2|\omega (\mu t){|}^{p_2}+M_f).\end{array}$$

Here we use the assumption that ${\sum }_{i=1}^{m-2}{\delta }_i{\eta }_i^q<1,$ the choice of $\lambda <1$ and consider $C_f=C_f^1+C_f^2,$ one have (7) $$\left|\right|\mathsf{G}\omega \left|\right|\le \frac{3(C_f|\left|\omega \right|{|}^{p_2}+M_f)}{\lambda \Gamma (q+1)}.$$(7)

□

Lemma 6.

G is a β-contraction operator with zero constant.

Proof.

Consider E is a bounded subset of B_k and a sequence $\left\{{\omega }_n\right\}$ in E, by using (7(7) $$\left|\right|\mathsf{G}\omega \left|\right|\le \frac{3(C_f|\left|\omega \right|{|}^{p_2}+M_f)}{\lambda \Gamma (q+1)}.$$(7) ) we have $$\left|\right|\mathsf{G}\omega \left|\right|\le \frac{3(C_f|\left|\omega \right|{|}^{p_2}+M_f)}{\lambda \Gamma (q+1)}.$$

Which show that $\mathsf{G}(E)$ is bounded. Now, for any $t_1<t_2 \in \mathsf{J},$ consider $$\begin{array}{l}|\mathsf{G}\omega (t_2)-\mathsf{G}\omega (t_1)|=|\frac{t_2^{n-1}-t_1^{n-1}}{\lambda \Gamma (q)}({\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\sum _{i=1}^{m-2}{\delta }_i{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\\ f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta )-\frac{1}{\Gamma (q)}{\int }_0^{t_1}((t_2-\zeta {)}^{q-1}-{(t_1-\zeta )}^{q-1})f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ -\frac{1}{\Gamma (q)}{\int }_{t_1}^{t_2}{(t_2-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta |,\\ \le (\frac{2|t_2^{n-1}-t_1^{n-1}|}{\lambda \Gamma (q+1)}+\frac{(t_2^q-t_1^q)+{(t_2-t_1)}^q}{\Gamma (q+1)})(C_f^1|\omega (t){|}^{p_2}+C_f^2|\omega (\mu t){|}^{p_2}+M_f).\end{array}$$

This shows that $\left\{\mathsf{G}{\omega }_n\right\}$ is equicontinuous as $t_2\to t_1.$ Hence by Arzelá-Ascoli theorem, $\mathbb{G}(E)$ is relatively compact in $\mathsf{X}.$ Thus by Proposition (2(2) $$\{\begin{array}{l}{}_0^C{D}_t^q\omega (t)+f(t,\omega (t),\omega (\mu t))=0, n-1<q\le n,\hspace{1em}0<\mu <1, t\in \mathsf{J}\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(i)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)+\mathsf{h}(\omega ),\hspace{1em}i=1,2,\dots ,n-2,\end{array}$$(2) ), $\mathsf{G}$ is β-contraction with zero constant. □

Theorem 2.

If the assumptions $({\mathbf{A}}_1)-({\mathbf{A}}_3)$ holds, then the BVP (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) has at least one solution ω and a bounded set of solutions in $\mathsf{X}$.

Proof.

By using Proposition 1, $\mathsf{T}$ is a strick β-contraction operator with constant K. Now consider $$\Lambda =\{\omega \in \mathsf{X}:\exists △\in [0,1] \mathit{such} \mathit{that} \omega =△\mathsf{F}\omega \}.$$

To show that Λ is bounded, one have $$\left|\right|\omega \left|\right|=\left|\right|△\mathsf{F}\omega \left|\right|=△\left|\right|\mathsf{F}\omega \left|\right|\le △(|\left|\mathsf{F}\omega \right||+|\left|\mathsf{G}\omega \right||).$$

In view of inequalities (6(6) $$\left|\right|\mathsf{F}\omega \left|\right|\le {\mathsf{C}}_g\left|\right|\omega |{|}^{p_1}+{\mathsf{C}}_h|\left|\omega \right|{|}^{p_1}.$$(6) ) and (7(7) $$\left|\right|\mathsf{G}\omega \left|\right|\le \frac{3(C_f|\left|\omega \right|{|}^{p_2}+M_f)}{\lambda \Gamma (q+1)}.$$(7) ) with $p_1<1, p_2<1,$ we can say that Λ is bounded in $\mathsf{X}.$ Hence by Theorem 1, There must be at least one fixed point of the operator $\mathsf{T}$ and a bounded set of fixed points in $\mathsf{X}.$ □

Consider that the following holds:

$({\mathbf{A}}_4)$ There exist a constat ${\mathcal{L}}_f>0$ such that $$|f(t,\upsilon ,\vartheta ))-f(t,\overline{\upsilon },\overline{\vartheta }|\le {\mathcal{L}}_f\left\{\right|\upsilon -\overline{\upsilon }|+|\vartheta -\overline{\vartheta }\left|\right\},\hspace{1em}\mathit{for} \mathit{each} \upsilon ,\vartheta ,\overline{\upsilon },\overline{\vartheta }\in \mathcal{R}$$

Theorem 3.

If the assumption $({\mathbf{A}}_1)-({\mathbf{A}}_4)$ holds, then the BVP (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) has a unique solution.

Proof.

For any $\omega ,\overline{\omega }\in \mathsf{X}$ and using the assumptions $({\mathbf{A}}_1)-({\mathbf{A}}_4),$ we have $$\begin{array}{l}|\mathsf{T}\omega (t)-\mathsf{T}\overline{\omega }(t)|\le (1-\frac{t^{n-1}\delta }{\lambda })|(\mathsf{g}(\omega )-\mathsf{g}(\overline{\omega }))|+\frac{t^{n-1}}{\lambda }|(\mathsf{h}(\omega )-\mathsf{h}(\overline{\omega }))|\\ +\frac{\left|t^{n-1}\right|}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))-f(\zeta ,\overline{\omega }(\zeta ),\overline{\omega }(\mu \zeta ))|d\zeta \\ +\frac{\left|t^{n-1}\right|\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))-f(\zeta ,\overline{\omega }(\zeta ),\overline{\omega }(\mu \zeta ))|\zeta \\ +\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}|f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))-f(\zeta ,\overline{\omega }(\zeta ),\overline{\omega }(\mu \zeta ))|d\zeta ,\\ \le ({\mathsf{K}}_g+{\mathsf{K}}_h+\frac{6{\mathcal{L}}_f}{\lambda \Gamma (q+1)})\left|\right|\omega -\overline{\omega }\left|\right|.\end{array}$$

This shows that $\mathsf{T}$ is a contraction, hence by Banach contraction principal the BVP (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) has a unique solution. □

4. Results devoted to stability

This section of our work, is devoted to Ulam type stability analysis for our proposed problem.

Definition 5.

The solution of our propose problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is Ulam-Hreys stable. If there exist $\mathfrak{L}>0$ be a constant, such that $\forall \omega \in \mathsf{X}$ and $\epsilon >0,$ we have (8) $${|}_0^C{D}_t^q\omega (t)-f(t,\omega (t),\omega (\nu t))|\le \epsilon ,t\in [0,1],$$(8) one has unique solution ${\omega }^{*}\in \mathsf{X}$ of the consider problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ), such that $$\left|\right|\omega -{\omega }^{*}\left|\right|\le \mathfrak{L}\epsilon .$$

And will be GUH stable, if we can find $$\Phi :(0,\infty )\to (0,\infty ),\Phi (0)=0,$$ such that $$\left|\right|\omega -{\omega }^{*}\left|\right|\le \mathfrak{L}\Phi (\epsilon ).$$

Definition 6.

The solution $\omega \in \mathsf{X}$ of our propose problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is UHR stable with respect to $\psi \in \mathsf{X}$ if there exist a positive constant $\mathfrak{L}$ such that for each $\omega \in \mathsf{X}$ and $\epsilon >0$ of the inequality (9) $${|}_0^C{D}_t^q\omega (t)-f(t,\omega (t),\omega (\nu t))|\le \psi (t)\epsilon ,\hspace{1em}\forall t\in [0,1],$$(9) one has unique solution ${\omega }^{*}\in \mathsf{X}$ of the consider BVP $(1),$ such that $$\left|\right|\omega -{\omega }^{*}\left|\right|\le \mathfrak{L}\psi (t)\epsilon .$$

And will be GUHR stable, if $$\left|\right|\omega -{\omega }^{*}\left|\right|\le \mathfrak{L}\psi (t).$$

Remark 1.

Let $\omega \in \mathsf{X}$ will be the solution of the inequality (8) if and only if, we have a function $\alpha \in C[0,1]$ depending on ω and for each $0\le t\le 1$

1. $|\alpha (t)|\le \epsilon ;$

2. ${}_0^C{D}_t^q\omega (t)=f(t,\omega (t),\omega (\mu t))+\alpha (t).$

Remark 2.

Let $\omega \in \mathsf{X}$ will be the solution of the inequality (9(9) $${|}_0^C{D}_t^q\omega (t)-f(t,\omega (t),\omega (\nu t))|\le \psi (t)\epsilon ,\hspace{1em}\forall t\in [0,1],$$(9) ) if and only if, we have a function $\alpha \in C[0,1]$ depending on ω and $\forall t\in [0,1]$

1. $|\alpha (t)|\le \epsilon \psi (t);$

2. ${}_0^C{D}_t^q\omega (t)=f(t,\omega (t),\omega (\mu t))+\alpha (t).$

Lemma 7.

Under the Remark 1, the function $\omega \in \mathsf{X}$ corresponding to the given problem $$\{\begin{array}{l}{}_0^C{D}_t^q\omega (t)+f(t,\omega (t),\omega (\mu t))=\alpha (t), n-1<q\le n,\hspace{1em}0<t,\mu <1\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(i)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)+\mathsf{h}(\omega )\hspace{1em}i=1,2,\dots ,n-2,\end{array}$$ satisfies the relation given by (11) $$|\omega (t)-\mathsf{H}(t,\omega (t),\omega (\mu t))|\le {\mathfrak{L}}_q\epsilon ,\forall t\in [0,1],$$(11) with $$\begin{array}{c}\mathsf{H}(t,\omega (t),\omega (\mu t))=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega )+\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta ,\end{array}$$ and $${\mathfrak{L}}_q=\frac{3}{\lambda \Gamma (q+1)}.$$

Proof.

With the help of Lemma 3, (10) becomes $$\begin{array}{c}\omega (t)=(1-\frac{t^{n-1}\delta }{\lambda })\mathsf{g}(\omega )+\frac{t^{n-1}}{\lambda }\mathsf{h}(\omega )+\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}f(\zeta ,\omega (\zeta ),\omega (\mu \zeta ))d\zeta \\ +\frac{t^{n-1}}{\lambda \Gamma (q)}{\int }_0^1{(1-\zeta )}^{q-1}\alpha (\zeta )d\zeta -\frac{t^{n-1}\sum _{i=1}^{m-2}{\delta }_i}{\lambda \Gamma (q)}{\int }_0^{{\eta }_i}{({\eta }_i-\zeta )}^{q-1}\alpha (\zeta )d\zeta -\frac{1}{\Gamma (q)}{\int }_0^t{(t-\zeta )}^{q-1}\alpha (\zeta )d\zeta ,\end{array}$$ which implies that $$|\omega (t)-\mathsf{H}(t,\omega (t),\omega (\nu t))|\le {\mathfrak{L}}_q\epsilon .$$

Theorem 4.

Under the assumption $({\mathbf{A}}_1)-({\mathbf{A}}_4)$, the solution of our proposed problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is UH and GUH stable, if $1\ne {\mathfrak{L}}_q.$

Proof.

In-view of Lemma 7, if ω is any solution and unique solution ${\omega }^{*}$ of consider problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ), such that $$\begin{array}{c}|\omega (t)-{\omega }^{*}(t)|=|\omega (t)-\mathsf{H}(t,{\omega }^{*}(t),{\omega }^{*}(\mu t))|\\ =|\omega (t)-\mathsf{H}(t,\omega (t),\omega (\mu t))+\mathsf{H}(t,\omega (t),\omega (\mu t))+\mathsf{H}(t,{\omega }^{*}(t),{\omega }^{*}(\mu t))|\\ \le |\omega (t)-\mathsf{H}(t,\omega (t),\omega (\mu t))|+|\mathsf{H}(t,\omega (t),\omega (\mu t))+\mathsf{H}(t,{\omega }^{*}(t),{\omega }^{*}(\mu t))|\\ \le {\mathfrak{L}}_q\epsilon +(K+2L_f){\mathfrak{L}}_q\left|\right|\omega -{\omega }^{*}\left|\right|\end{array}$$ which further yields that $$\left|\right|\omega -{\omega }^{*}\left|\right|\le \frac{{\mathfrak{L}}_q}{1-(K+2L_f){\mathfrak{L}}_q}\epsilon .$$

Expressing by $\mathfrak{L}=\frac{{\mathfrak{L}}_q}{1-(K+2L_f){\mathfrak{L}}_q},$ then the propose problem (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is UH stable. Also, if $\Phi (\epsilon )=\epsilon ,$ then the concerned solution is GUH stable. □

Lemma 8.

For the problem (10), the following inequality holds: $$|\omega (t)-\mathsf{H}(t,\omega (t),\omega (\mu t))|\le {\mathfrak{L}}_q\epsilon \Psi (t),\text{for}\mathsf{ }\text{all}t\in [0,1],$$

Proof.

We omit the proof, just similar to that of Lemma 7 by using Remark 2. □

Theorem 5.

The solution of our propose model (1(1) $$\begin{array}{c}{}_0^C{D}_t^q\omega (t)=-\omega (t), 0<q\le 1,\hspace{1em}0<t<1\\ \omega (0)={10}^6,\end{array}$$(1) ) is UHR and GUHR stable, if ${\mathfrak{L}}_q\ne 1$, assumption $({\mathbf{A}}_1)-({\mathbf{A}}_4)$ hold along with Lemma 8.

Proof.

We omit the proof, for the reader. □

5. Verification of our main results by a test problem

Example 1.

Consider the multi-points BVP (12) $$\begin{array}{c}{}_0^C{D}_t^{\frac{5}{2}}\omega (t)=\frac{|\omega (t){|}^{\frac{1}{3}}+|\omega \left(\frac{t}{4}\right){|}^{\frac{1}{3}}}{(9+e^t)|\omega (t){|}^{\frac{1}{3}}},\hspace{1em}0<t<1\\ \omega (0)=\mathsf{g}(\omega )\hspace{1em}{\omega }^{(1)}(0)=0,\hspace{1em}\omega (1)=\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)+\mathsf{h}(\omega ),\hspace{1em}\sum _{i=1}^{m-2}{\delta }_i\omega ({\eta }_i)=\frac{1}{5}.\end{array}$$(12)

Take $q=\frac{5}{2}, p_1=1, p_2=△=\frac{1}{3}, \gamma =2\in (1,3), {\mathcal{L}}_f={\mathcal{K}}_f=\frac{1}{5}, {\mathcal{M}}_f=0, {\mathcal{K}}_g={\mathcal{K}}_h=\frac{1}{6};$ The assumption $({\mathbf{A}}_1)-({\mathbf{A}}_4)$ holds. The solution of the BVP (12) is given by $$\omega (t)=[1-t]\mathsf{g}(\omega )+t(\frac{2}{5}+\mathsf{h}(\omega )){-}_0{I}^{\frac{5}{2}}f(t,\omega (t),\omega (\frac{t}{4})){+}_0{I}^{\frac{5}{2}}f(1,\omega (1),\omega (\frac{1}{4})).$$

Here $\mathsf{F}\omega (t)=[1-t]\mathsf{g}(\omega )+t(\frac{2}{5}+\mathsf{h}(\omega ))$ and $\mathsf{G}\omega (t)={-}_0{I}^{\frac{5}{2}}f(t,\omega (t),\omega (\frac{t}{4})){+}_0{I}^{\frac{5}{2}}f(1,\omega (1),\omega (\frac{1}{4})).$ Since $\mathsf{F}, \mathsf{G}$ are continuous and bounded so is $\mathsf{T}=\mathsf{F}+\mathsf{G}.$

Further $$\left|\right|\mathsf{F}\omega -\mathsf{F}\overline{\omega }\left|\right|\le \frac{1}{3}\left|\right|\omega -\overline{\omega }\left|\right|,$$ so $\mathsf{F}$ is β-contraction and $\mathsf{G}$ is β-contraction with zero constant, shows that $\mathsf{T}$ is strick β-contraction with constant $\frac{1}{3}.$ by Theorem 1 the BVP (12) has a solution in $\mathsf{X}=C[0,1].$ Also ${\mathfrak{L}}_q=2.2567,$ So by Theorem 4 the solution of BVP (12) is UH and GUH stable. In a similar way, we can see that the BVP (12) is UHR and GUHR stable by using Theorem 5 and considering $\Psi (t)=t.$

6. Conclusion

In this article, we have developed some adequate results about the existence and stability for a class of multi-points BVP of FDEs with delay term. We have used Kuratwoski measure of non-compactness and topological degree concept to derive the required results. By pertinent example, the results have been demonstrated. Further the problem under consideration is nonlocal problem such like problem often occurred in application in many disciplines of engineering, fluid mechanics, etc.

Authors’ contribution

All authors have equal contribution.

Acknowledgement

We are thankful to the referees comments which has improved this paper very well.

Disclosure statement

No potential conflict of interest was reported by the authors.