Implementation of Alternative Grading Methods in a Mathematical Statistics Course

Abstract

Alternative grading methods, such as standards-based grading, provide students multiple opportunities to demonstrate their understanding of the learning outcomes in a course. These grading methods allow for more flexibility and help promote a growth mindset by embracing constructive failure for students. Implementation of these alternative grading methods requires developing specific, transparent, and assessable standards. Moving away from traditional methods also requires a mindset shift for how both students and instructors approach assessment. While providing multiple opportunities is important for learning in any course, these methods are particularly relevant to an upper level mathematical statistics course where topics covered often provide an additional challenge for students as they lie at the intersection of both theory and application. By providing multiple opportunities, students have the space for constructive failure as they tackle learning both a conceptual understanding of statistics and the supporting mathematical theory. In this article we share our experiences—including both challenges and benefits for students and instructors—in implementing standards-based grading in the first semester of a mathematical statistics course (i.e., focus primarily on probability). Supplementary materials for this article are available online.

Keywords:

• Assessment
• Growth mindset
• Probability course
• Standards-based grading

1 Introduction

When we think of grading, what comes to mind? Unfortunately, the response may differ depending on whether you are asking a student versus an instructor. As statistics educators, we strive to align our assessment of students with their learning and understanding of the material through continuous feedback; however, students often focus on what will get them the most points and that “A” grade. Although never the intention, students may successfully pass a course based primarily on partial credit without ever fully learning any concepts. Ideally, we want to remove the distraction of points in how we assess students and use an assessment method which emphasizes student growth, learning, and understanding. Garfield (1994) echoes the importance of tying assessment to students’ learning and how, for example, traditional grading of tests does not fully capture student understanding. Cobb (1993) further states the importance of assessment for student learning: “Responsibility for the process of learning cannot be shared unless the way to assess its quality is authentic, public, clearly understood, and accepted by the students.”

One of the guidelines in the revised Guidelines for Assessment and Instruction in Statistics Education (GAISE) college report (GAISE College Report ASA Revision Committee 2016) emphasizes the importance of using “assessments to improve and evaluate student learning.” Thus, sharing of ideas to connect student learning and understanding with assessment is not new in statistics education. For example, Chance (1997) highlights ways in which we can rethink what areas are emphasized when we grade as well as thinking about different assessment methods outside of just written exams. Garfield (1994) and Garfield and Gal (1999) provide principles on assessment for statistics educators, including an assessment framework and suggestions for both assessment methods (e.g., quizzes, projects, written reports) and evaluation (scoring rubrics and feedback). Some alternative assessment instruments such as orally recorded exam feedback (Jordan 2004), writing assignments (Woodard, Lee, and Woodard 2020), and computer-assisted assessment (Massing et al. 2018) seek to expand options for statistics educators and how they assess student learning. O’Connell (2002) uses a variety of different assessment methods for a multivariate analysis course including: structured data analysis, open-ended research and data analysis reports, analyzing research articles, and annotating computer output. Konold (1995) presents challenges when it comes to assessing conceptual understanding, while others have addressed how to tackle these challenges with new assessment techniques. For example, Chance (2002) and Hubbard (1997) provide examples of questions aimed at assessing students’ statistical thinking and understanding of concepts. Green and Blankenship (2015) explore methods of assessment through active learning in order to encourage conceptual understanding of concepts in a mathematical statistics course. Broers (2009) also advocates for the importance of conceptual understanding—sharing a method which combines open questions, partial concept maps, and propositional manipulation (Broers 2002).

Many of these examples provide innovative methods in terms of connecting what is assessed (e.g., a focus on conceptual understanding and statistical thinking) to how it is assessed (e.g., projects, open-ended questions, writing assignments) in our statistics courses. In this article, we take another approach and explore alternative methods for the assessment structure itself. Our goal is to move away from points-based assessment methods and use a structure built to encourage a growth mindset and one centered around students demonstrating the learning outcomes of a course.

When we as statistics educators think of assessment, we often strive to assess student learning and provide feedback for our students. As Chance (2002) states, “The number one mantra to remember when designing assessment instruments is ‘assess what you value.”’ The work shared in this article was first motivated by a concern that traditional grading was not successfully achieving our goal of assessing student learning and understanding. In particular, for courses that build off each other, these authors were seeing a disconnect in learning when students reached the second-semester course. For example, students may have received a passing grade to get to the second semester course; however, they may not have fully learned and understood the important concepts from the first semester. The alternative grading methods we outline in this work seek to address these concerns. Instead of using a traditional point-based system, we allow students to continually revise their work until reaching a desired learning outcome. As we outline in the following section, these ideas build upon Garfield’s (1994) one suggestion for assessing projects and written reports in statistics courses where “the student [is allowed] to revise and improve the product until it meets the instructor’s standard.”

To help increase awareness of alternative grading practices to the statistics education community, we aim to provide helpful resources and insights on implementation of these methods for interested statistics educators. In what follows, we provide a brief overview of what we are referring to as “alternative grading,” followed by a description of our approach to implementing one type of alternative grading in the first semester of a mathematical statistics course. In addition to our own reflections on the implementation, we share student progress data and student feedback regarding their views of the alternative grading used in the course.

2 What Do We Mean by Alternative Grading?

Although terminology and details can vary, the alternative grading methods shared here follow some core principles (Campbell, Clark, and O’Shaughnessy 2020):

1. There are clear and transparent learning outcomes that are assessable;

2. Students are assessed on whether they demonstrate an understanding of the outcome (assessment is not for points and thus there is no partial credit); and,

3. Students have multiple opportunities to demonstrate understanding for each outcome, either through revising and resubmitting the same problem or by retesting a different problem.

In application, two common forms of alternative grading include standards-based grading and specifications-based grading. Although the specifics for the implementation of each of these methods will vary by instructor and course (see Cilli-Turner et al. 2020 for some ideas on building a syllabus centered around the above principles), we outline the main features of each below. More details on how we implemented these methods in the first semester of a mathematical statistics course (i.e., focus primarily on probability) are shared in the next section.

Standards-based grading is focused on tying a student’s final grade to a set of learning outcomes, or standards. Each assignment is associated with a set of learning outcomes on which the student is assessed (principle #1). Instead of using a point-based system, each learning outcome is assessed on whether or not the student achieved success in meeting the outcome where the student does not receive credit until they reach a successful mark (principle #2). Students are allowed multiple attempts to reach a successful mark, whether it be to revise a prior example or retest on a new question (principle #3). The final course grade is typically determined by the amount of successfully met learning outcomes. See, for example, Campbell, Clark, and O’Shaughnessy (2020), Elsinger and Lewis (2020), Selbach-Allen et al. (2020), and Zimmerman (2020).

Specifications-based grading takes on many of the same characteristics as standards-based grading. Here each assignment is assessed on a set of clear specifications where students receive a successful mark if all specifications on that assignment are satisfactorily met (principles #1 and #2). Specifications-based grading is often found to be useful for assignments such as projects or writing assignments. As with standards-based grading, students are given the opportunity to revise their work in order to reach a successful mark (principle #3). The course grade is typically determined by the amount of successfully completed assignments. See, for example, Campbell, Clark, and O’Shaughnessy (2020), Carlisle (2020), Nilson (2015), Prasad (2020), Reyes (2021), and Tsoi et al. (2019).

By following the above principles, we attempt to address the earlier mentioned goal regarding tying students’ learning to how we assess. Because there is no partial credit, these alternative grading methods encourage complete demonstration of standards or specifications for a student to be successful. By implementing these alternative grading methods, we further introduce more flexibility for students as they have multiple opportunities to demonstrate understanding which allows for varied pacing. This varied pacing makes it possible for all students, regardless of background or preferred learning style, to be successful (Feldman 2018). Because students need to revisit (revise or redo) standards or specifications they miss, these alternative grading methods embrace constructive failure and promote a growth mindset. The fact that students are given the time to learn at their own pace allows them to build confidence in their abilities and worry less about a single exam or project. In this light, alternative assessment is an equitable practice. One of the driving principles in Grading for Equity states that, “the way we grade should motivate students to achieve academic success, support a growth mindset, and give students opportunities for redemption,” and how the practice of standards-based grading, “simplifies what a grade represents and how it is earned, empowering and enlisting students to self-identify areas of strength and weakness, and to know precisely what it takes to succeed” (Feldman 2018).

3 Development and Implementation

After understanding the concepts and philosophies behind alternative grading, we (the authors) chose to implement a standards-based assessment system in the first semester of a traditional mathematical statistics course starting in Fall 2020. While we teach at small, private, liberal arts institutions (Gustavus Adolphus College and Moravian University), the cohorts of students in our classes vary slightly.

Gustavus Adolphus College offers a major in Statistics and the year-long mathematical statistics course is a requirement for all students pursuing a major. The first semester in the year-long mathematical statistics course (henceforth we will call this course Math Stat I) is offered every fall semester (15 week semester) at Gustavus and has a prerequisite of multivariable calculus and discrete mathematics. Classes meet four days a week, for 50 min, and the course typically enrolls 8–16 students. In Fall 2020, Moravian University offered a Mathematics major and a Data Science track within the Computer Science major. Math Stat I is an applied elective for students pursuing a Math major and a required course for students pursuing a Computer Science major on the Data Science track at Moravian. This course is taught every other fall semester (15 week semester) and has a Calculus II prerequisite. Classes meet three days a week, for 70 min, and the course typically enrolls 7–18 students. Despite the differences in prerequisites and the majors being served by the course, Math Stat I at both Gustavus and Moravian covers nearly identical content, focusing primarily on probability and probability distributions (and both requiring the textbook Mathematical Statistics with Applications, by Wackerly, Mendenhall, and Scheaffer 2014), which led to our collaboration.

3.1 Standards

The first step to implementing a standards-based grading system is to develop assessable standards. For a standard to be assessable, it needs to be measurable and address a single learning objective. To get started, we looked at the learning outcomes from our previous Math Stat I syllabi and quickly realized that those outcomes were not measurable nor did they address a single learning objective. As an example, a learning outcome used in prior semesters of Math Stat I was, “Students will be able to understand a variety of probability distributions and real world situations that give rise to them.” This learning objective does not indicate what we expect the student to be able to do and it is unclear how “understanding” will be measured.

Unable to use previous course learning objectives, we decided to start by identifying the main units we cover in the course. We came up with six units focused on probability, discrete probability distributions, continuous probability distributions, moment generating functions, functions of random variables, and multivariate probability distributions. For each of these units, we used past exams and homework questions to help determine which learning objectives we viewed as most important, making sure we also identified why each learning objective was important, how the learning objective might be linked to another learning objective in the course, and where in Bloom’s taxonomy the learning objective would be classified (Anderson and Krathwohl 2001). While developing these standards, we found collaboration to be crucial as the conversations we had enabled us to really evaluate, and justify why, each standard was important. Through this process, we were able to settle on a final list of 27 standards that we believed appropriately identified what we hoped students would be able to do by the end of the semester. The full list of standards can be found in the supplementary materials. We do note that, due to the differences in the prerequisites for the courses at our two institutions, the standards in the sixth unit, multivariate probability distributions, were assessed differently. At Moravian, all multivariate standards were assessed using discrete distributions, with the joint probability distribution often being given in a table. At Gustavus, the multivariate standards were assessed using a combination of discrete and continuous probability distributions, because the students all had previously taken multivariate calculus.

3.2 Course Structure and Assessments

Once we had a list of measurable learning objectives for the course, we needed to determine how to assess whether students met a learning objective and whether there would be any other assessments in the course not directly linked to the course standards. We decided to have four types of assessments in our Math Stat I Course: learning community assignments, portfolio problems, tests, and a final exam.

The learning community assignments were low-stakes assignments to encourage participation in the class as well as participation in department or institution activities. As an example, one learning community assignment at Gustavus was to attend a visiting speaker’s talk and submit a reflection on how the ideas from the class were incorporated into what the speaker discussed. A common type of learning community assignment at both Gustavus and Moravian was to complete an example started in class or to watch a short video of a concept and then complete a problem based on the content of the video. Each learning community assignment was graded on a two-tiered scale: “Meets Expectations” or “Does Not Meet Expectations.” The requirements for what it meant to meet expectations were posted with each assignment; where, typically, a submission was successful based solely on completion or sufficient effort shown (e.g., the student used statistical justification in their response such as using a reasonable definition or property learned in class). At Gustavus, there were 37 learning community assignments over the semester, while Moravian had 42. As most of these assignments were meant to prepare students for a given day in class, the students only had one attempt at a learning community assignment; thus, if a student failed to submit a particular assignment, they earned a “Does Not Meet Expectations.”

The portfolio problems were similar to traditional homework problems. During the semester, there were eleven sets of portfolio problems, each set containing anywhere from three to eight problems. The portfolio problems covered the material being taught in the course, with some portfolio problems directly corresponding to a single course standard while other portfolio problems corresponded to more than one course standard. Gustavus students were given a total of 57 problems in the 11 sets while Moravian students were given a total of 49 problems. The difference in the number of problems for the two courses was based on instructor preference; however, most of the portfolio problems were the same.

Each portfolio problem was marked on a four-tiered scale: Success (S), Success* (S*), Growing (G), and Not Yet (N). A mark of “S” indicated that the student completed the problem correctly, including using accurate statistical notation. An “S*” was given if the student completed the problem correctly save for a minor algebraic or calculus mistake. A mark of “G” indicated that the student was making progress on the problem, but still needed to make some changes to get the problem correct. A mark of “N” was given for incomplete problems or problems attempted using incorrect methods. Just as in any traditionally graded course, essential feedback was given with suggestions for how to work toward the correct answer, if necessary. A portfolio problem earning an “S” or an “S*” was deemed sufficient to earn credit. Students could revise any problem earning a “G” or an “N” and resubmit their revisions within one week. Students were allowed to work together or seek help from the instructor on portfolio problems as long as the problem write-up was their own.

There were four tests given during the semester. Each question on a test was directly linked to one of the 27 standards. As some standards required demonstration of more than one technique, 10 of the 27 standards were assessed using multiple questions, while the remaining 17 standards were assessed using a single question. (The specific standards assessed using multiple questions are marked in the documents shared as part of the supplementary materials.) Like with portfolio problems, each question on a test was marked on a four-tiered scale, using the same four tiers as before (S, S*, G, and N). If a student earned an S on all questions corresponding to a standard, they “met” the standard. The mark of S* indicated that students would need to just revise that question in order to receive a successful “S” mark; they did not need to continue testing for that standard. If a student earned a “G” or an “N” on a question, the student did not demonstrate understanding of the corresponding standard for that question and was given an opportunity to retest the standard the following week by attempting another question or set of questions.

As an example, one standard states: “Determine the probability distribution of a function of random variables using one of the appropriate methods (distribution method, univariate transformation method, or moment-generating function method).” As we wished students to show some breadth in their understanding of these different methods, there were two questions that corresponded to this standard on the fourth test in the course. A student needed to earn an S or an S* (and correctly fix the S*) on both questions to get credit for meeting this standard. If a student earned an S on one question and a G on the other question, they did not meet the standard and thus needed to reattempt two different questions for that standard when they retested.

Each student was guaranteed three attempts at each standard on the tests, though the testing structure varied by institution. At Gustavus, where students met in class four days a week for 50 min, reattempts at testing were done during class so that testing was reserved for one class day each week of the semester, save for the first three weeks. At Moravian, where students met in class three days a week for 60 min,¹ the initial test was given during class time, but the retesting was done outside of class time during office hours or an alternate scheduled appointment with the instructor. To allow for flexibility, students were given five “extra chances” to reattempt a standard (after they had exhausted their guaranteed three attempts). To earn an extra chance, students had to submit a form indicating which standard they wanted to reattempt and what they had done to practice or study for the reattempt.

The final exam was cumulative and included a subset of standards from throughout the course. Like the tests during the semester, each question on the final was marked using the same four-tiered scale. Unlike tests during the semester, each standard was linked to only one question, and a student “met” the standard if they earned an S or an S* (as there was no time left in the semester to make corrections).

Thus, students were evaluated on four assessment categories. Learning community assignments were non-evaluative assessments meant to encourage preparation, practice, and engagement. Portfolio problems and tests were non-traditionally graded assessments in which students either demonstrated understanding or not (no partial credit), but students had multiple opportunities to show whether they grasped the content. The final exam was the one assessment category that most resembled traditional grading as students did not have multiple attempts at the final. However, we believed a cumulative assessment was a way for students to see how all of the topics connected and we adjusted for the lack of multiple attempts by adjusting the cutoff for the final exam within the larger determination of their final course grade and allowing an S* to count as a successful mark (see next section).

Despite the shift in assessment and time needed for re-testing, the day-to-day classroom activities remained relatively the same for both authors, albeit some minor changes did occur. For example, spending the time to develop the standards helped us focus on what learning outcomes were most important and led us to prioritize certain classroom activities/examples over others. In transitioning to the new grading system, we also created more videos for students to watch outside of class (i.e., watched as part of their learning community assignments), allowing more time in class to work through examples in small groups of 2–3 students and time for the re-testing. So, for example, transitioning to alternative grading would likely work well for those instructors who use a flipped classroom pedagogy.

3.3 Equating Performance on Assessments to Course Grades

Because both Moravian and Gustavus require submission of a final letter grade, we needed to translate student performance on the four assessment categories into a letter grade. We did this by defining a baseline letter grade determined by the percentage of “S” marks a student received in each of the four assessment categories. A student’s baseline grade was the best letter grade for which the cutoffs for all four assessment types were met. The cutoffs for determining the baseline grade are shown in Table 1.

Table 1 Cutoffs for determining baseline grade based on the four assessment categories.

Baseline Grade	A	B	C	D	F
Tests	$\ge 90\%$ of standards with S	$\ge 80\%$ of standards with S	$\ge 70\%$ of standards with S	$\ge 60\%$ of standards with S	<60% of standards with S
Portfolio Problems	$\ge 90\%$ of standards with S/S*	$\ge 80\%$ of standards with S/S*	$\ge 70\%$ of standards with S/S*	$\ge 60\%$ of standards with S/S*	<60% of standards with S/S*
Learning Community Assignments	$\ge 90\%$ of items meet expectations	$\ge 80\%$ of items meet expectations	$\ge 70\%$ of items meet expectations	$\ge 60\%$ of items meet expectations	<60% of items meet expectations
Final Exam	$\ge 80\%$ of standards with S/S*	$\ge 70\%$ of standards with S/S*	$\ge 60\%$ of standards with S/S*	$\ge 50\%$ of standards with S/S*	<50% of standards with S/S*

As seen in Table 1, the cutoffs for a grade on the tests, portfolio problems, and learning community assignments are all the same, but the cutoffs for the final exam differ. As mentioned earlier, this is because the final exam does not allow for reattempts, thus, we decided to lower the grade threshold. The rubric in Table 1 was used to determine the baseline grades for all students. For example, if a student earned an S on 73% of the test standards, got an S or S* on 81% of portfolio problems, met expectations on 86% of learning community assignments, and earned an S/S* on 68% of the final exam standards, the student would have a baseline grade of C.

Once we established a student’s baseline grade, we wanted to account for the fact that a student’s baseline grade could be impacted negatively by a single assessment category. To do this, we determined final course grades by taking a student’s baseline grade and modifying it based on the number of assessment types that were in a higher grade cutoff. The specifics for determining the final course grade are shown in Table 2. We do acknowledge, however, that the final course grade determination in Table 2 is not perfect. For example, consider the student who does well in the course but has one bad day on the final exam. As with any new pedagogical practice, we recognize the importance to continually improve, as is further discussed in Section 5.

Table 2 Final course grade determination based on baseline grade and performance in the four assessment categories.

Baseline Grade	Performance in 4 Assessment Categories	Final Course Grade
A	–	A
B	3 “A” cutoffs met	A–
	2 “A” cutoffs met	B+
	0 or 1 “A” cutoffs met	B
C	3 “B” (or higher) cutoffs met	B–
	2 “B” (or higher) cutoffs met	C+
	0 or 1 “B” (or higher) cutoffs met	C
D	3 “C” (or higher) cutoffs met	C–
	2 “C” (or higher) cutoffs met	D+
	0 or 1 “C” (or higher) cutoffs met	D
F	3 “D” (or higher) cutoffs met	D–
	0, 1, or 2 “D” (or higher) cutoffs met	F

Consider again the example student referenced earlier that earned an S on 73% of the test standards, got an S or S* on 81% of portfolio problems, met expectations on 86% of learning community assignments, and earned an S/S* on 68% of the final exam standards. This student had a baseline grade of C. However, the final course grade for this student would have been a C + since the student met the “B” cutoff for two assessment categories (portfolio problems and learning community standards).

3.4 Mid-Semester Changes to Implementation

Like every semester, especially those in which new pedagogy is used, not all implementation went exactly as planned and we needed to make some adjustments mid-semester. Most of the adjustments made had to do with timing and being able to cover all 27 standards while allowing for at least three testing attempts. Specifically, at Gustavus, the tests only ended up covering the 19 standards in the first five units. The eight standards in the sixth unit were not tested during the semester and the standard, “Calculate expectations and variances for real world applications of hierarchical models” was not covered in the Gustavus course due to time constraints.

Thus, Gustavus students ended up with 26 total standards for the course, with 19 of the standards being tested during the semester. The remaining seven standards not tested during the semester were on the final exam (and the students were aware that those seven standards were guaranteed to be on the final). The final at Gustavus was composed of 14 total standards, so the remaining seven standards on the final were a subset of the 19 previously tested standards. Students were not aware which of the previous standards seen would appear on the final exam at Gustavus.

The course at Moravian was able to cover more content and thus the Moravian students ended up with the full 27 total standards. However, like at Gustavus, the Moravian students were only able to test on 22 of the 27 during the semester. The five untested standards were guaranteed to be on the final exam along with nine previous standards already tested in the course. The Moravian students were aware that the five untested standards would be on the final, but did not know which of the already tested standards would be included. Both Gustavus and Moravian had a total of 14 standards on the final (approximately half of the total course standards).

A second change mid-semester arose from student requests. Multiple students at both Gustavus and Moravian wanted a third attempt at portfolio problems. Given the adjustment to the new grading system and some progress by students being a bit slower than we initially expected, we were in favor of allowing an additional attempt as ultimately this still supported our goal of learning for the students. To allow for this, without completely changing the structure of the course, we let students use an “extra chance” (originally intended only for additional reattempts on a test standard) on a set of portfolio problems (Gustavus) or a single portfolio problem (Moravian). Students were still limited to five “extra chances” for the semester, but the ability to use them on portfolio problems allowed for more flexibility for students.

Overall, in our development and implementation of Math Stat I, we tried to adhere to the principles of alternative grading. Students were given clear learning outcomes, each outcome was marked as met or not, and multiple attempts were given to meet an outcome. We felt the time and energy dedicated to transitioning Math Stat I to alternative grading was well worth it and we were generally satisfied with how the semester went. However, we knew that collecting data on student outcomes and experiences in our courses would be paramount to informing continued use of alternative grading.

4 Instructor Reflections and Student Feedback

As with implementing any new pedagogical practice into the classroom, alternative grading brought about its challenges. However, we believe the benefits—as seen from our viewpoint as well as the students—outweighed any challenges.

4.1 Challenges

From the instructors’ perspective, there were challenges in both developing the course under the new grading system, as well as with the implementation throughout the semester. The biggest challenges included: developing assessable learning outcomes, developing multiple questions to measure said learning outcomes, creating an understandable grading scheme, ensuring student buy-in, and time management with the frequent grading sessions.

As discussed in an earlier section, learning outcomes for the course needed to be revisited to ensure they were assessable. Along with defining the learning outcomes, a variety of questions measuring each of these learning outcomes were compiled (to ensure we had questions for students’ multiple attempts at a standard). These tasks required devoted time and collaboration. Thus these challenges were linked to a shift in the timing of the workload—needing more preparation time prior to the semester starting. As an example, prior to the first semester using standards-based grading in our mathematical statistics course, we spent much of the summer developing standards and questions to assess those standards. We created roughly four questions for each standard to be utilized in testing, essentially writing all exams before the semester even began.

Another challenge in the development stages was in determining a final grading scheme. Despite the course being assessed on demonstrating understanding of learning outcomes, final letter grades were still necessary at the end of the semester. When establishing a final grading scheme, there is a tricky balance between having one that is accurate yet also understandable (Talbert 2021). For example: How many standards must be met to achieve an A?; Do you create separate criteria for different assessment categories?; How much will a final exam count toward the final grade?; etc.

Once the semester starts, an ongoing challenge can be building student trust and buy-in for the new grading scheme. Switching from the comfortable, traditional grading system to that of alternative grading requires a shift in mindset for many students. Early and consistent messaging is needed. Some suggestions include introducing the concept of a growth mindset through conversations, consistent messaging, activities, and/or assignments (Elsinger and Lewis 2020, Kelly 2020). Other challenges come from a need to adjust our own mindsets when it comes to grading throughout the semester. As students are allowed multiple opportunities to demonstrate understanding, this requires setting aside time to grade new submissions every week.

We also gathered data from an anonymous student survey about their perspective of the alternative grading system. All student data was collected after receiving approval from the Gustavus Adolphus College Institutional Review Board (approval #012875) as well as obtaining informed consent from the students. From the students’ perspective, when asked “What do you like least about standards based grading? That is, what are some negative aspects?” some common themes from students across both institutions included:

• frustrations with no partial credit and the higher standards for receiving a successful mark, for example,

I don’t like that everything is graded more strictly. For example, on a test if I make a mistake on one aspect of a standard, I have to retest on the whole standard, even if I got all the other parts right, compared to a regular course where I would have just gotten partial credit for the problem I made a mistake in.

Not having partial credit can be frustrating when I am on the right track but can’t fully solve the problem.

It can be very frustrating when you get close to passing a standard but not quite there. In a normal class where you might get 85%, which is fairly respectable, you end up getting it completely wrong. However, while it is frustrating, I think along with the ability to retry multiple times it ends up leading to better learning.

It was frustrating to get one problem right for a standard, but not the other, so you end up getting no credit.

• time management and the amount of work required to be successful, for example,

It’s easy to fall behind if you’re not keeping up with the work. I like that I have this type of grading for my upper level classes and in general. But I’m not sure if people would like it in their lower level courses.

I think the my least favorite part about the grading is how things can pile up fast if you are trying to retest on standards that you had problems with in the past.

It takes a lot more work and time and it is hard to manage with other classes.

In the beginning, when I hadn’t quite got into a rhythm or felt as comfortable asking for help I was struggling to do the amount of work…. I just let it pile up and it stressed me out a lot in the beginning before I understood when I needed to ask for help and how I needed to manage my time.

• recognizing the distinctions between the marks of S, S*, G, and N, for example,

The line between each level of grading is somewhat vague. I am not sure what is required for an S vs G.

I feel like it needs to more consistent between G and S* and that sometimes things graded as G deserved to be S*

I also feel as though sometimes the grading is very harsh, as a student could have everything correct and mistakingly chose the wrong bound, restriction, or limit (etc.) and receive a growing (G) instead of a success upon revision (S*), which kind of takes motivation away if that was the only issue when solving a single problem/standard.

• and concerns with how the final letter grade was determined, in particular with how heavily weighted the final exam was, for example,

The only aspect I would recommend change for would probably be how the final is factored into the final grade. It just feels like the final holds too much weight in regards to the philosophy of standards based grading.

I didn’t like how difficult it was to calculate my grade.

The biggest concern truly is the Final and the weight, as a student with a “perfect grade” or 100% before the final can go from a perfect A to a D-, which takes away all of their hard work during the semester, giving it no value at all in my opinion through this structure.

4.2 Benefits

Despite some of the challenges, meaningful benefits were noted by both instructors and students alike. From the instructors’ perspective, some of the biggest benefits included: having transparent outcomes to share with students, having shorter grading sessions, witnessing student growth, increased opportunities for student success, and having student buy-in.

As mentioned earlier, developing the assessable standards did require substantial time prior to the first semester ever teaching under the new grading system. However, with standards-based grading, the resulting learning outcomes were shared with, and tracked by, the students which allowed for improved transparency—thus, making it worth the effort spent in developing them. One of the challenges mentioned was the frequent grading sessions; however, as standards-based grading entails simply recognizing successful work (or not) without the headache of determining partial points, grading sessions were shorter than with traditional grading.

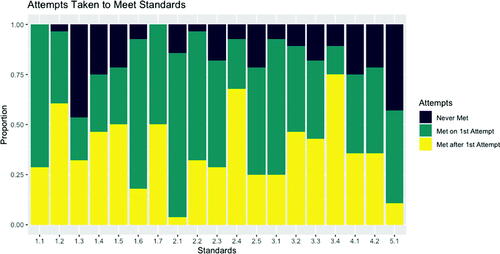
Perhaps one of the most meaningful benefits was that of student growth and increased opportunities for success. Seeing students actually revisit their mistakes on tests and assignments was encouraging. Many students, from both institutions, also benefited from the opportunity of multiple attempts to demonstrate their understanding (as illustrated by the bottom, yellow bars in Figure 1). These data support how traditional deadlines imposed on students may limit their ability to learn at their own pace; in particular for students with diverse or weaker educational backgrounds (Feldman 2018). Further, since students were allowed multiple attempts and each question was specifically tied to a given learning outcome, we as instructors felt there were increased opportunities to both identify and address universally challenging learning outcomes as well as support individually struggling students as they grew and learned from their mistakes.

Fig. 1 Number of attempts students took to obtain a successful mark on each learning outcome. Data are for $n=$ 28 students from both Gustavus and Moravian (100% response rate); results are combined as there were no striking differences between the institutions.

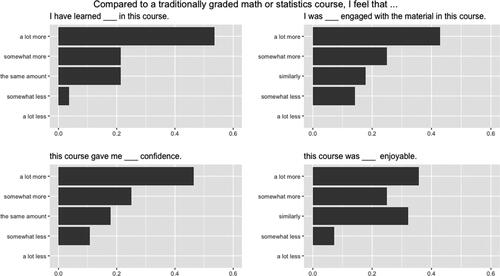
Although student buy-in can be a challenge at first, by the end of the semester we also saw student buy-in as a benefit of using alternative grading. Overall we were happy to see that the majority of students appreciated the learning, the engagement, the confidence, and enjoyment of the course supported by using alternative grading in the course. For example, as seen in Figure 2, the majority of students felt that they learned more, were more engaged, had more confidence, and thought the course was more enjoyable as compared to a traditionally graded math or statistics course. In fact, when students at Gustavus Adolphus College² were asked whether they would prefer standards-based grading or traditional grading for their follow-up second semester mathematical statistics course, 11 of 13 (85%) of them were in support. Based on the open-ended questions of the survey, when asked “What do you like best about standards based grading? That is, what are some positive aspects?” common themes from students at both institutions included:

Fig. 2 Student responses when asked to compare alternative grading to traditionally graded math or statistics courses. Data are for $n=$ 28 students from both Gustavus and Moravian (100% response rate); results are combined as there were no striking differences between the institutions.

• an appreciation for focusing on learning over earning points, for example,

I really like that it tests our knowledge of the topic rather than our ability to get points.

I really liked that it gave me a chance to see when I didn’t fully understand concepts because I have gotten so used to receiving partial grades that are high enough that I don’t bother to look them over or care about the parts that I didn’t get completely correct. I appreciated the opportunity to focus on the parts I didn’t understand and work to make sure that I did understand, instead of focusing on my ability to just memorize for and pass a test.

I like that I have the chance to keep learning a topic rather than just cram for a topic to get the most points possible on a test.

I like that it forces you to actually pay attention to the material and internalize it better. For many classes you do everything you can to get as many points as possible on assignments and tests, but then a few months later you don’t remember anything about it. I hope with this method I will retain the actual information and material for a long time after the class.

• the opportunities to learn and grow from their mistakes, for example,

It gave me the opportunity to pinpoint my mistakes and learn from them rather than just see them and move on.

The standard based grading, and regrading attempts, made it so that you still learned a concept after it was tested. In other courses, you were tested then moved on and may or may not talk about that topic. Since stats kept building on itself, the retesting for standards helped for making sure your foundation was solid.

I like being able to retake things and actually being “forced” to understand the content to get it 100% correct instead of making up half of the problem and getting half credit and never seeing it again.

It focuses on my complete understanding of the concept instead of my ability to just memorize a type of problem. I also like that a “growing” is much more encouraging than getting a “C”. It encourages growth instead of labeling as mediocre.

• the flexible pacing and ability to retest and revise, for example,

I liked that we were able to have second chances because there were times when I really needed to use the second chances because I did not get the concepts from the first time.

I liked that I had more ability and time to master a topic without falling behind in class.

I like that we get multiple attempts for each standard. This proves that this type of grading focused more on making sure students are actually learning and understanding the material.

I like having several chances to complete a problem correctly. This motivates me to revisit problems that I initially struggled with.

I liked being able to re-do problems. I wasn’t able to forget about problems that I made mistake on because I had to “master” them in order to continue. I like have multiple chances in general. I think it makes learning a lot easier.

• and reduced stress and anxiety when it came to tests, for example,

I like that we get multiple attempts to do homework problems and tests. This ensures that we are fully understanding the material and alleviates some of pressure and anxiety that can occur during an exam.

Less stressful because you aren’t expected to know everything 100% the first time because there is that room to grow

I felt more relaxed for the exams since there was always the option of retaking parts

I’m not a good test taker (I get anxious and rushed during exams), so that is another reason why I like having multiple attempts. I can take my time.

5 Ongoing Changes to Implementation

Based on the instructors’ reflections as well as feedback from students, we have already started moving forward with changes to our implementation of standards-based grading in the Math Stat I course. One change includes updating the list of standards so that each standard is only measuring a single objective. As an example, “Prove events are disjoint or independent,” was a standard in our first implementation and a test would incorporate two questions (one for disjoint, one for independence) where students would only receive credit for the standard if they were successful in both questions. To minimize frustration from students, and provide more clarity, we split this standard into two separate standards: one for proving events are disjoint and one for proving events are independent. This way, if a student earns an S on one question and an N on the other question, they are able to receive recognition for the one standard they were successful on without having to test on proving both disjoint and independent events again. Additionally, the standard, “Calculate expectations and variances for real world applications of hierarchical models,” was cut altogether due to insufficient time during the semester to both learn, test, and have the opportunity to retest on it. This topic can still be explored in the course, but is not a standard that is being evaluated. A full list of the updated standards are found in the supplementary materials.

In addition to changing the standards themselves, we also updated how assessment is done. The learning community assignments are handled in the exact same manner. The portfolio problems are handled similarly, except students are given three attempts (instead of two) and each problem is graded on a three-tiered scale (instead of a four-tiered scale). The three tiers now used are Success (S), Success* (S*), and Not Yet (N). The “S” and “S*” marks mean the same thing as the first implementation and portfolio problems earning either an “S” or “S*” are sufficiently successful. A mark of “N” is given for any problem not earning an “S” or “S*.” Students can revise and resubmit any problem earning an “N.” Changing from a four to a three-tier scale was done to eliminate student confusion regarding the difference between an “N” and a “G” or a “G” and an “S*” as well as to streamline the grading process for the instructor.

To ensure students have the opportunity for multiple tries at each test standard, the schedule of the tests underwent a big shift from the first iteration. There are still four tests throughout the semester, but they are now spaced such that the last week and half of the course is dedicated to testing and retesting the last set of standards so that all course standards are evaluated during the semester. As with the first iteration, the assessment of the test questions mirrors that of the portfolio problems—just now both assessment categories use the updated three-tiered scale.

To provide more transparency, we moved the grade modifiers to be tied with just the final exam, lending itself to a simpler grade determination for the students (Table 3). This way students knew exactly where they stood in the class going into the final exam. With the shift to more opportunities to meet the baseline grade cutoffs (e.g., more learning outcomes and the last week being devoted to retesting), we were comfortable switching from a system that seemed to better account for the fact that a student’s baseline grade could be impacted negatively by a single assessment category (Table 2) to one with increased simplicity and transparency (Table 4). In the updated grading scheme, the learning community assignments, portfolio problems, and tests still determine the baseline grade for students, as shown in Table 3; however, the baseline grade calculation no longer includes the final exam. As before, the baseline grade is the best letter grade for which the cutoffs for all three assessment categories are met.

Table 3 Updated cutoffs for determining baseline grade from the three assessment categories.

Baseline Grade	A	B	C	D	F
Tests	$\ge 90\%$ of standards with S	$\ge 80\%$ of standards with S	$\ge 70\%$ of standards with S	$\ge 60\%$ of standards with S	<60% of standards with S
Portfolio Problems	$\ge 90\%$ of standards with S/S*	$\ge 80\%$ of standards with S/S*	$\ge 70\%$ of standards with S/S*	$\ge 60\%$ of standards with S/S*	<60% of standards with S/S*
Learning Community Assignments	$\ge 90\%$ of items meet expectations	$\ge 80\%$ of items meet expectations	$\ge 70\%$ of items meet expectations	$\ge 60\%$ of items meet expectations	<60% of items meet expectations

Table 4 Updated final course grade determination defined by the baseline grade and performance on the final exam.

Final exam performance	Final course grade
standards with S/S* $\ge$ 85%	Baseline grade +
70% $\le$ standards with S/S* <85%	Baseline grade
50% $\le$ standards with S/S* <70%	Baseline grade–
standards with S/S* <50%	Lower baseline grade by one full letter

In an effort to give less weight to the final exam, and better adhere to the principles of alternative grading, it is now used as a “grade modifier” rather than one of the components determining the baseline grade. As before, the final exam is made up of 14 questions, each corresponding to a course standard. The baseline grade and the final exam performance again determine the final course grade, as outlined in Table 4.

As an example, if a student came in with a baseline grade of “B” and got an S/S* on 93% of the standards on the final exam, the student would earn a final course grade of B+. If a student came in with a baseline grade of “B” and earned an S/S* on 43% of the standards on the final exam, the student would earn a course grade of C. This method of using the final exam to modify the base grade along with the cutoffs used comes from Robert Talbert’s blog post, “Specifications grading: We may have a winner” (Talbert 2017).

With these changes to the implementation of standards-based grading in Math Stat I, we hope to see some of the prior challenges and student frustrations minimized. Of course, improvements and changes will likely not stop here, as we continue to tweak our implementation of alternative grading in Math Stat I.

6 Conclusion

Alternative grading methods allow students multiple opportunities to demonstrate complete understanding of transparent learning outcomes. What we have shared in this work represents one possible implementation of alternative grading practices as applied to an upper-level mathematical statistics course. It should be noted that alternative grading need not solely follow the framework of standards-based grading as we have shared here. Instructors have the flexibility to mix and match different facets to best fit the needs of their students and their statistics course. Although not a focus of our work at this time, interested individuals can also look into building on concepts from other common alternative grading methods such as specifications-based grading (Nilson 2015) or un-grading (e.g., contract grading) (Kohn and Blum 2020).

Despite the challenges in implementing alternative grading, both students and instructors saw benefits in the opportunities for students to grow and learn as they shifted their mindset to focus less on points and focus more on learning. Although no formal assessment was completed, these authors have noticed that students in the second semester of the mathematical statistics course sequence do appear more engaged and prepared in the material—one of our original goals for implementation in these courses. Those students who would struggle in the second semester due to passing the first semester course by partial credit alone, are now being flagged earlier on. Further, having clearly outlined learning outcomes allowed us, as instructors, to clearly reference past standards from the first semester during the second semester. For example, when discussing pivotal quantities we could reference the prior learning outcome of transformation methods.

We recognize that our implementation was for a relatively small sample size and specific to smaller liberal arts institutions; however, we hope that interested instructors can still benefit from our shared resources and reflections on implementing alternative grading in an upper-level probability statistics course. We hope that instructors interested in pursuing alternative grading methods in their statistics courses are motivated and encouraged to build off our work and adapt the methods to their own courses. Different course content and cohorts of students may require a change in our approach to alternative grading (e.g., a project in introductory statistics assessed using specifications grading in place of a final exam); however, we would expect that interested instructors who adhere to the principles of alternative grading shared here would experience similar benefits, regardless of the course or type of institution.

Acknowledgments

We would like to thank Anna Peterson and Ulrike Genschel for their invaluable help in constructing assessable learning outcomes.

Supplementary Materials

Included in the supplementary materials are the standards used for the first semester of a mathematical statistics course for both the first and second implementation of teaching the course with standards-based grading.

Disclosure Statement

The authors report there are no competing interests to declare.

Notes

1 Although typically 70 minute classes, due to scheduling shifts with the pandemic, classes were reduced to 60 minutes during the Fall 2020 semester.

2 Given the schedule of courses at Moravian University, these students did not have the opportunity to take the follow-up mathematical statistics course during the 2020–2021 academic year.