Abstract
There is a wide variation of the reported experimental data of moisture diffusivity of solid food materials, making difficult their utilization in drying and other applications. Published values of moisture diffusivity in various foods were retrieved from the literature, and these were classified and analyzed statistically to reveal the influence of material moisture content and temperature. Empirical models, relating moisture diffusivity to material moisture content and temperature, were fitted to all examined data for each material. The data were screened carefully using residual analysis techniques. The most promising model was proposed, which is based on an Arrhenius-type effect of temperature and it uses a parallel structural model to take into account the effect of material moisture content.
INTRODUCTION
Literature data for moisture diffusivity in foods materials were selected and presented in a recent review by Panagiotou et al. Citation[3]. Moisture diffusivity depends strongly on moisture, temperature and structure of the material. In porous materials, the void fraction, and the pore structure and distribution affect diffusivity significantly. Limited information concerning the effect of structure on diffusivity is available in the literature. On the other hand, the effect of moisture and temperature on diffusivity has been studied more extensively. Nevertheless, general models describing the effect of moisture and temperature on diffusivity do not exist. A large number of empirical equations are summarized and analyzed in detail by Marinos-Kouris and Maroulis Citation[2] and Zogzas et al. Citation[4]. According to the most popular consideration, an Arrhenius model is adopted for the effect of temperature and the effect of moisture is introduced into the Arrhenius parameters. The scope of the paper is (a) to propose a mathematical model and calculate the moisture diffusivity of some food materials as a function of temperature and moisture, and (b) to fit the model simultaneously to all available literature data and to obtain higher accuracy in estimation of the moisture diffusivity in foods.
MATHEMATICAL MODEL
The transport of moisture within solid or semi-solid foods can be expressed by the effective diffusivity (D), which is an overall transport property, accounting for all transport mechanisms in the liquid and gas phases. Suppose that a material with intermediate moisture of a uniform mixture of two different materials (a) a dried material and (b) a wet material with infinite moisture. Moisture diffusivity is, generally, different for each material. The diffusivity of the mixture could be estimated using a two phase structural model:
Suppose that the diffusivities of both phases depend on temperature by an Arrhenius-type model:
| Tr = 60°C | = |
a reference temperature, |
| R = 0.0083143 | = |
kJ/kg mol K the ideal gas constant, and |
| Do , Di , Eo , Ei = | = |
adjustable parameters of the proposed model. |
The reference temperature of 60°C was chosen as a typical temperature of air-drying of foods. Thus, the moisture diffusivity for every material is characterized and described by four parameters with physical reasoning:
| Do (m2/s) | = |
Diffusivity at moisture X = 0 and temperature T = Tr |
| Di (m2/s) | = |
Diffusivity at moisture X = ∞ and temperature T = Tr |
| Eo (kJ/mol) | = |
Activation Energy for diffusion in dry material at X = 0 |
| Ei (kJ/mol) | = |
Activation Energy for diffusion in wet material at X = ∞ |
Table 1. Mathematical Model for Calculating Moisture Diffusivity as a Function of Moisture and Temperature
PROCEDURE OF REGRESSION ANALYSIS
The proposed model is fitted to data using a non linear regression analysis method. It is fitted to all literature data for each material and the estimates of the model parameters are obtained. Then the residuals are examined and the data with large residuals are removed. The procedure is repeated until an accepted standard deviation between experimental and calculated values is obtained Citation[1].
RESULTS AND DISCUSSION
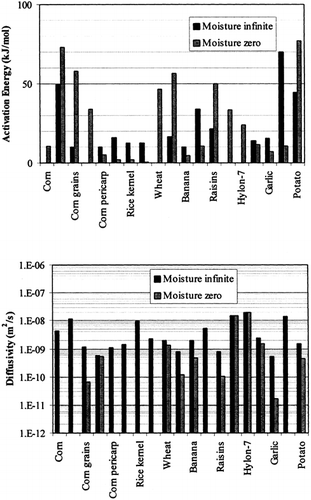
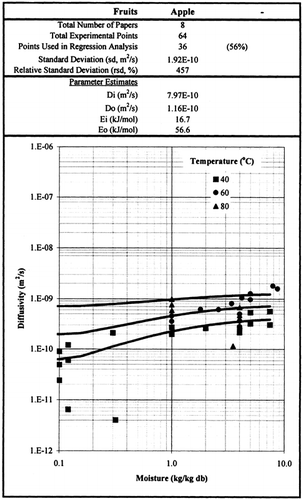
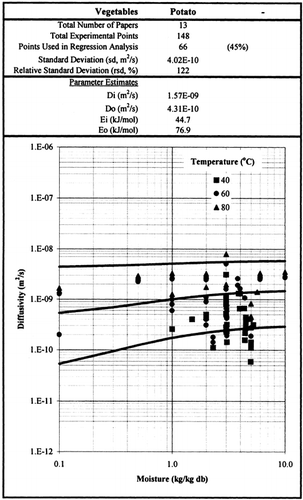
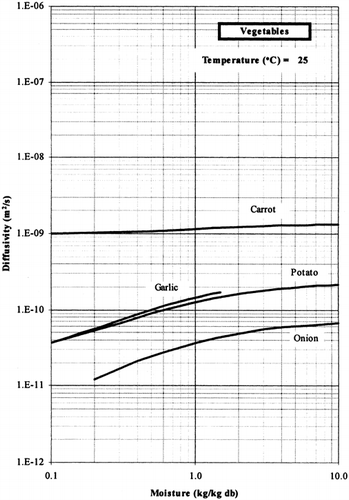
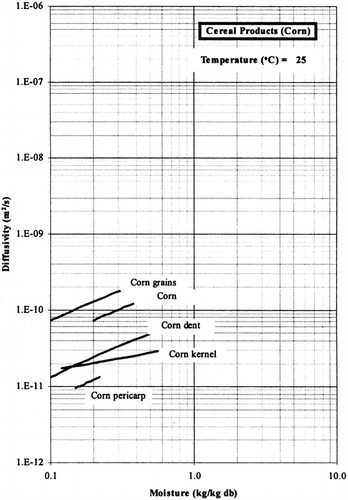
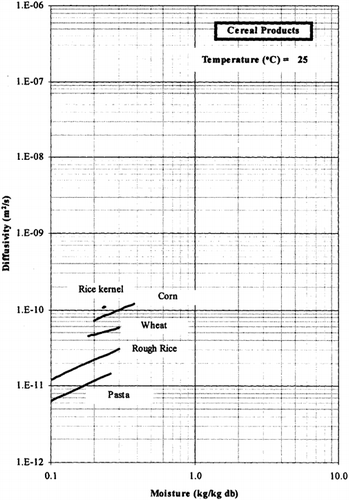
Among the available data only 19 materials have more than 10 data, which come from more than 3 publications. The procedure is applied to these data and the results of parameter estimation is presented in Table and in Figure . It is clear that moisture diffusivity is larger in wet materials. Figures present the retrieved data from the literature and the model calculated values for selected materials. Figures summarize the model predicted values for various materials for selected food categories at ambient temperature. It must be noted that the regression procedure was applied simultaneously to all the data of each material, regardless of the data sources. Thus, the results are not based on the data of only one author and consequently they are of higher accuracy and general applicability.
Figure 1. Parameter estimates of the proposed model of Table .
Figure 2. Effective moisture diffusivity of Corn Grains at various temperatures and moisture contents.
Figure 3. Effective moisture diffusivity of Apple at various temperatures and moisture contents.
Figure 4. Effective moisture diffusivity of Potato at various temperatures and moisture contents.
Figure 5. Predicted values of moisture diffusivity for fruits.
Figure 6. Predicted values of moisture diffusivity for vegetables.
Figure 7. Predicted values of moisture diffusivity for various grains.
Figure 8. Predicted values of moisture diffusivity for cereal products.
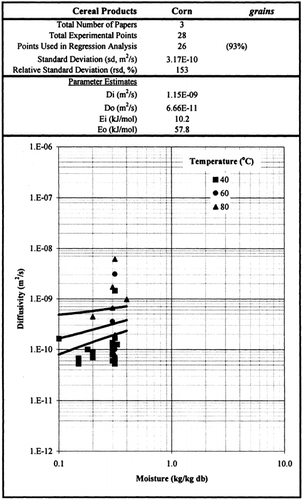
Table 2. Parameter Estimates of the Model Presented in Table
The diffusivity parameters Do and Di of the proposed model, shown in Figure , vary in the range of 10−10 to 10−8 m2/s. It should be noted that the self-diffusivity of water is approximately 10−8 m2/s, and the moisture diffusivity in bone-dry food material should be lower (in our analysis, by a factor of 100). Low moisture diffusivities are found in non-porous and sugar-containing foods, while higher values of moisture diffusivity characterize porous food materials.
The moisture diffusivity increases, in general, with increasing moisture content. Temperature has a positive effect, which depends strongly on the food material. The energy of activation for diffusion (E) of water is, in general, higher in the dry food materials. Some observed exceptions may be explained by the prevailing type of diffusion. Thus, lower values of activation energy for diffusion are expected for porous foods, where vapor diffusion is significant.
CONCLUSION
The well known parallel model was fitted adequately to moisture diffusivity literature data for some foods. The results obtained have reasonable accuracy, however adequate data exist only for limited materials to carry out a successful regression.
Acknowledgments
REFERENCES
- Draper , N. and Smith , H. 1981 . Applied Regression Analysis, Second Edition New York : Wiley .
- Marinos-Kouris , D. and Maroulis , Z. B. 1995 . “ Thermophysical Properties for the Drying of Solids ” . In Handbook of Industrial Drying Edited by: Mujumdar , A. New York : Marcel Dekker .
- Panagiotou , N. M. , Krokida , M. K. , Maroulis , Z. B. and Saravacos , G. D. in press . Moisture Diffusivity: Literature Data Compilation for Foodstuffs . International Journal of Food Properties ,
- Zogzas , N. , Maroulis , Z. B. and Marinos-Kouris , D. 1996 . Moisture Diffusivity Data Compilation in Foodstuffs . Drying Technology , 14 ( 10 ) : 2225 – 2253 .