The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities

Abstract

Introduction: The molecular mechanics energies combined with the Poisson–Boltzmann or generalized Born and surface area continuum solvation (MM/PBSA and MM/GBSA) methods are popular approaches to estimate the free energy of the binding of small ligands to biological macromolecules. They are typically based on molecular dynamics simulations of the receptor–ligand complex and are therefore intermediate in both accuracy and computational effort between empirical scoring and strict alchemical perturbation methods. They have been applied to a large number of systems with varying success.

Areas covered: The authors review the use of MM/PBSA and MM/GBSA methods to calculate ligand-binding affinities, with an emphasis on calibration, testing and validation, as well as attempts to improve the methods, rather than on specific applications.

Expert opinion: MM/PBSA and MM/GBSA are attractive approaches owing to their modular nature and that they do not require calculations on a training set. They have been used successfully to reproduce and rationalize experimental findings and to improve the results of virtual screening and docking. However, they contain several crude and questionable approximations, for example, the lack of conformational entropy and information about the number and free energy of water molecules in the binding site. Moreover, there are many variants of the method and their performance varies strongly with the tested system. Likewise, most attempts to ameliorate the methods with more accurate approaches, for example, quantum-mechanical calculations, polarizable force fields or improved solvation have deteriorated the results.

Keywords:

• drug design
• electrostatics
• entropy
• free energy perturbation
• linear interaction energy
• non-polar solvation
• solvation

1. Introduction

A goal of structure-based drug design is to find a new pharmaceutical compound that binds to a macromolecular receptor. In essence, the binding can be described with the chemical reaction:

1

where L denotes the ligand and R the receptor (which typically is a protein or another biomacromolecule). The binding strength is determined by the binding free energy, ΔG_bind. Traditionally, design campaigns are carried out experimentally, a process that is both time-consuming and costly. Therefore, computational methods have been developed with the aim of reducing the time and cost to design new drugs. The choice of method depends on at which stage in the campaign it will be employed and there is typically a trade-off between accuracy and efficiency.

The most widely used computational methods in drug design are docking and scoring [1], whereby the binding mode of the drug is predicted, followed by an estimate of the binding affinity. These methods are efficient but not particularly accurate; they can be used to predict binding modes and discriminate between binders and non-binders, but they can typically not discriminate between drugs that differ by less than one order of magnitude in affinity, that is, by < 6 kJ/mol in ΔG_bind.

At the other end of the spectrum there are the alchemical perturbation (AP) methods that are derived from statistical mechanics and thus are in principle very accurate [2]. However, they are based on Monte Carlo or molecular dynamics (MD) simulations and require extensive sampling of the complex and the free ligand in solution, as well as of unphysical intermediate states, which render them computationally intensive. Therefore, they have seldom been used in drug design [3].

Between these extremes there is a group of methods with intermediate performance. They are also based on sampling but only of the end states, that is, the complex and possibly the free receptor and ligand. These methods are therefore called end point methods. They were devised to be more inexpensive than AP, but more accurate than the scoring functions.

The most basic approximate method is the linear-response approximation (LRA) [4], in which the electrostatic free energy change is estimated from

2

where is the electrostatic interaction energy between the ligand and the surroundings (the receptor or water), the brackets indicate ensemble averages and their subscripts indicate from which simulation the average is computed. PL and L are standard simulations of the complex and the ligand, respectively, whereas PL′ and L′ indicate simulations in which the charges of the ligand have been zeroed. This method has been used to estimate solvation free energies, but not binding free energies because it lacks a non-polar part. However, it forms the basis of the linear interaction energy (LIE) method developed by Åqvist et al. [5,6]. In this method, only the complex and the free ligand is simulated. In addition, a non-polar term is added, formed in an analogous way:

3

where is the van der Waals interaction between the ligand and the surroundings, and α and β are empirical parameters. Warshel et al. have devised a related method called PDLD/s-LRA/β (semi-macroscopic protein-dipoles Langevin-dipoles method within a LRA) [4], in which the polar part is LRA and the non-polar part is borrowed from LIE.

The arguably most popular end point method is the topic of this review: MM/PBSA (molecular mechanics [MM] with Poisson–Boltzmann [PB] and surface area solvation) [7]. In this method, ΔG_bind is estimated from the free energies of the reactants and product of the reaction in Equation 11 :

4

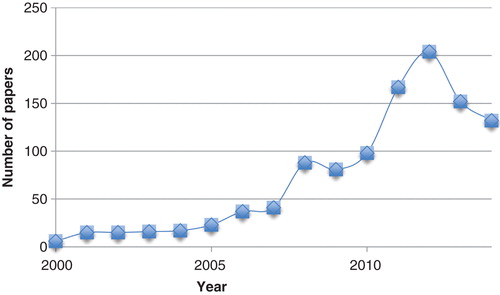
This method was developed by Kollman et al. in the late 90s [8] and has enjoyed a high popularity ever since, with 100 – 200 publications each of the latest 5 years, as can be seen in Figure 1. The method has been used in a range of settings, including protein design [9], protein–protein interactions [10,11], conformer stability [12,13] and re-scoring [14,15]. In this paper, we present a critical review of the method and its ability to predict ligand-binding affinities. In particular, we discuss the precision and accuracy of the results and whether it is possible to improve the method by using more accurate approaches for each of the terms in the method, whereas specific applications are better covered in previous reviews [7,16-18]. Several methods with similarity to MM/PBSA have been suggested both earlier and later [19-21], but none of them has found any wide application.

Figure 1. The number of hits per year in Web of Science when searching for the topics MM/PBSA, MM-PBSA, MM/GBSA or MM-GBSA.

2. The MM/PBSA approach

Here, we will describe the MM/PBSA approach as it was originally defined by Kollman et al. [7,8]. Since then, the method has been developed and modified [16-18] and we will discuss many variants in the coming sections. Unfortunately, there is still no consensus on the details of the method, probably because the performance varies depending on what system it is applied to.

In MM/PBSA, the free energy of a state, that is, P, L or PL in Equation 44 , is estimated from the following sum [7,8]:

5

where the first three terms are standard MM energy terms from bonded (bond, angle and dihedral), electrostatic and van der Waals interactions. G_pol and G_np are the polar and non-polar contributions to the solvation free energies. G_pol is typically obtained by solving the PB equation or by using the generalized Born (GB) model (giving the MM/GBSA approach), whereas the non-polar term is estimated from a linear relation to the solvent accessible surface area (SASA). The last term in Equation 55 is the absolute temperature, T, multiplied by the entropy, S, estimated by a normal-mode analysis of the vibrational frequencies. Gohlke and Case have pointed out that a correction owing to the translational and rotational enthalpy (3 RT) was missing in the original formulation and that the translational entropy should be calculated with a 1 M concentration standard state to be comparable to experimental estimates [11].

Strictly, the averages in Equation 44 should be estimated from three separate simulations [22], that is, from simulations of the complex, the free ligand and the unbound receptor, thereby obtaining

6

where the subscripts indicate from which simulation the average is computed. We will denote this approach three-average MM/PBSA (3A-MM/PBSA).

However, it is much more common to only simulate the complex and create the ensemble average of the free receptor and ligand by simply removing the appropriate atoms, thereby obtaining

7

which we will denote one-average MM/PBSA (1A-MM/PBSA). This requires fewer simulations, improves precision and leads to a cancellation of E_bnd in Equation 55 . On the other hand, it ignores the change in structure of the ligand and the receptor upon ligand binding, which may be important factors for the affinity [22]. We compared the 3A- and 1A-MM/PBSA approaches for the avidin and factor Xa (fXa) proteins, but unfortunately the performance depended on the test system and solvation model [23]. However, the standard error was four to five times larger with the 3A-MM/PBSA approach. In another study of the ferritin protein [24], the large uncertainty of the 3A approach (19 – 21 kJ/mol) rendered the results practically useless. Pearlman drew a similar conclusion for p38 MAP kinase [25]. In practice, the 1A approach often gives more accurate results than the 3A approach [26,27]. Swanson et al. suggested a 2A approach with sampling also of the free ligand, which would include the ligand reorganization energy [22]. Yang et al. have made a similar argument and have shown that it can improve the results [28].

Typically, the simulations used to estimate the ensemble averages in Equations 66 and 77 employ explicit solvent models. All solvent molecules are then removed from each snapshot, because the implicit PBSA or GBSA solvent models are used to estimate the solvation energies. However, this leads to an inconsistency in the method because the simulations and energy calculations do not use the same energy function, requiring reweighting of the energies. This could be circumvented by simulating with the same implicit solvent model used when evaluating the free energy. However, the accuracy of the implicit solvent model is uncertain and sometimes leads to dissociation of the ligand or protein subunits [29]. We have illustrated this problem by performing both implicit and explicit solvent simulations of five galectin-3 complexes [30]: Ensembles generated by the different solvent models are rather different with root-mean-square deviations of 1.2 – 1.4 Å and the quality of the predicted affinities changes significantly. It was possible to convert one ensemble into the other by performing simulations with the new method, but the convergence was slow.

It has often been suggested that the MM/PBSA calculation can be based on single minimized structures, rather than on a large number of MD snapshots. Naturally, this will save much computational effort, but it also ignores dynamical effects, making the results strongly dependent on the starting structure, and all information about the statistical precision of the method is lost. Yet in practice, minimized structures often give as good or better results as MD simulations [15,31-33], although some studies have emphasized the importance of MD sampling [14]. We have tested this approach by starting the minimization from different MD snapshots and shown that it often gives results similar to those obtained with MD, but sometimes unrealistic structures need to be filtered away [29]. It has been argued that more time can be saved by performing the minimizations in a GB continuum solvent [32]. Hou et al. found that the MM/GBSA results varied with the length of the MD simulation, but that there is no gain of using simulations longer than 4 ns [33]. Finally, it has been suggested that the results can be improved by using NMR ensembles, rather than MD simulations [34].

The MM/PBSA approach was originally developed for the AMBER software [7,8] and several automated versions have been presented [35,36]. Recently, automatic scripts have also been presented for the freely available GROMACS, NAMD and APBS software [37].

3. The precision

Early applications of MM/PBSA used relatively few snapshots (∼ 20) from the MD simulations. A typical result is shown in Table 1. It can be seen that for charged ligands (Btn1 – Btn3), the MM/PBSA energy is dominated by the E_el and G_pol terms, but these two terms often nearly cancel, illustrating the screening effect of the solvent. Consequently, the E_vdW term often dominate the net binding free energy, although the entropy term is also sizeable. On the other hand, the G_np term is essentially always small and similar for all ligands.

Table 1. The various MM/PBSA terms (cf. Equation 55 ) for the binding of seven biotin analogues to avidin (kJ/mol).

Term	Btn1	Btn2	Btn3	Btn4	Btn5	Btn6	Btn7	SD1	SD7
Eel	–1224	–1295	–1287	–174	–83	–50	–109	46	21
EvdW	–148	–149	–132	–200	–128	–128	–49	16	11
Gpol	1224	1321	1259	266	146	123	124	30	13
Gnp	–17	–17	–17	–21	–16	–16	–11	0	0
TS	–81	–96	–70	–82	–67	–66	–28	46	57
Eel + Gpol	0	26	–27	92	63	72	15	22	20
ΔGbind	–187	–145	–222	–114	–49	–34	–53	47	62

The two last columns (SD1 and SD7) show the standard deviation of the various terms for Btn1 and Btn7. Ligands Btn1–Btn3 have a net charge of –1, whereas the other four ligands are neutral.

Adapted with permission from [29] (the 03oh/03 calculation with PB solvation). Copyright (2006) American Chemical Society.

A major problem with MM/PBSA is the poor precision. For example, the standard deviation of ΔG_bind over the 20 snapshots in Table 1 (SD1 and SD7 columns) is 47 and 62 kJ/mol, giving a standard error of the mean of 11 and 14 kJ/mol (i.e., the standard deviation divided by the square root of the number of snapshots). Such a poor precision makes the method useless when comparing ligands with similar affinities or when comparing results obtained with different approaches or by different groups. Therefore, we made a thorough investigation how statistically converged MM/GBSA results can be obtained [38]. We showed that it is more effective to run many short independent simulations than a single long, which has also been observed in other studies [39-41] (a single long simulation will underestimate the uncertainty in the result). Moreover, we showed that snapshots taken after 1 – 10 ps are statistically independent and that an equilibration of 100 ps and a production simulation of 100 – 200 ps are appropriate, although later studies have indicated that occasionally longer equilibrations are needed [42]. Once these measures have been determined, any desired precision can be obtained by running a proper number of independent simulations, because the standard error decreases with the square root of the number of independent samples. For avidin, 20 – 50 simulations were needed to give a standard error of 1 kJ/mol for the seven biotin analogues (6 – 15 ns simulations for each ligand in total).

We have also discussed how the independent simulations should be generated [42]. The standard way is to use different starting velocities for the MD simulations. However, the variation can be enhanced by taking advantage of the arbitrary choices made when setting up the MM/PBSA calculations, in particular the solvation of the receptor and the selection of alternative conformations in the starting crystal structure. The uncertainty in the protonation and conformation of various groups can also be employed with some care. The good message of our results is that the MM/GBSA results are insensitive to all these choices, unless the affected residue is very close to the ligand. This shows that MM/GBSA is stable and reproducible and that calculations set up by different groups and procedures are likely to give similar results, in spite of the many more or less arbitrary choices made during the setup.

4. The polar solvation term

The polar solvation term (G_pol in Equation 55 ) was originally obtained by solving the PB equation numerically [7,8]. However, it can in principle be calculated with any other continuum-solvation method and it is now more common that it is calculated by the GB approach (giving a MM/GBSA method), because such calculations are faster and pair-wise decomposable. Many studies have compared the performance of MM/PBSA and MM/GBSA, indicating that the MM/PBSA results are better [29,33], worse [14,43-45] or of a similar quality [15,32,46,47], depending on the studied system.

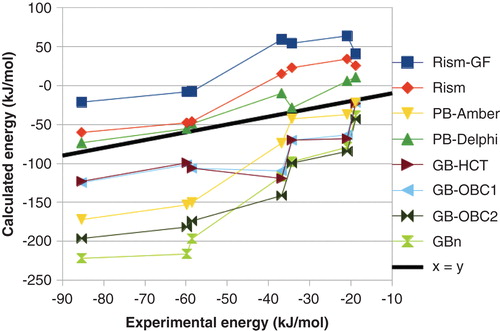
Gohlke and Case have made a detailed study on how the results depend on the polar solvation energy [11]. They find that the PB results strongly depend on the radii employed and that different variants of GB give widely different results. We have also tested several different methods [48]. As can be seen in Figure 2, there was a major variation in the absolute ΔG_bind obtained with the various methods, up to 210 kJ/mol, and even the relative affinities varied by up to 85 kJ/mol. The mean absolute deviation (MAD) between the calculated and experimental ΔG_bind varied from 10 to 43 kJ/mol (after removal of the systematic error) and the correlation coefficient (r²) varied from 0.59 to 0.93. We also tested two variants of the three-dimensional reference site interaction model (3D-RISM), which is expected to give more accurate solvation energies, but it gave intermediate results (r² = 0.80 – 0.90 and MAD = 16 – 17 kJ/mol).

Figure 2. Dependence of the MM/PBSA results on the continuum-solvation model for the binding of seven biotin analogues to avidin.

It has also been suggested that special methods can be used for the ligand, for example, a LIE-like solvation term [49]. We have compared the performance of 24 different continuum-solvation methods [50]. For small organic molecules, the quantum mechanics (QM)-based polarized continuum model (PCM) gave the most accurate results, but the performance deteriorates as the size and polarity of the molecule increase and if we compare only relative solvation energies of homologous ligands with the same net charge, essentially all methods (PCM, PB and GB) give solvation energies that agree within 2 – 5 kJ/mol. This indicates that there is not much to gain from using more accurate solvation methods for the ligand.

5. The non-polar solvation term

The polar solvation energy represents the electrostatic interaction between the solute and the continuum solvent. However, three additional terms are needed to reproduce experimental solvation energies, viz. cavitation, dispersion and repulsion energies, representing the cost of making a cavity in the solvent, as well as the attractive and repulsive parts of the van der Waals interactions between the solute and the solvent. Strictly, all these three non-polar solvation terms are free energies and in particular the cavitation energy should have important entropic components, representing the reorganization of the solvent around the solute [16]. However, in standard MM/PBSA, the non-polar solvation energy is represented by a linear relation to the SASA [7].

This term has been little discussed, although the parameters vary quite extensively, 0.01 – 0.24 kJ/mol/Ų for the surface tension and 0 – 4.2 kJ/mol for the offset [8,9,16,17,29,44]. The reason for this is that the term is typically small and shows only a minor variation among similar ligands (Table 1), thereby having insignificant influence on the results. This is alarming, as this term should model the hydrophobic effect, which normally is assumed to be among the most important terms for ligand binding [1]. It has sometimes been argued that the SASA model should be completed with the solvent–solute van der Waals interaction [11,16] or that only the attractive part of the van der Waals interaction should be included [51]. Solvent-accessible volume terms have also been tested, but without changing the results significantly [37].

We noted that the non-polar solvation energy calculated by SASA is three to eight times smaller and of the opposite sign to the same energy calculated by the more accurate PCM (which includes separate terms for cavitation, dispersion and repulsion energies) or 3D-RISM methods [48,52]. By calibration against AP calculations with explicit water for the binding of benzene to a hidden cavity in T4 lysozyme, we showed that actually both methods give the wrong results, because they assume that the cavity is filled with water before the ligand binds, contrary to experimental observations [53]. If this problem is corrected by filling the un-bound cavity with a non-interacting ligand, PCM actually gives a more accurate result than SASA. Unfortunately, for more water-exposed binding sites, both SASA and PCM fail strongly (by up to 32 and 78 kJ/mol, respectively) to reproduce the AP results and it seems to be hard to find any correction that works for binding sites of different solvent accessibility [54]. The reason for this is that the continuum methods do not contain any information about how many water molecules there are in the binding site and their entropy before and after the ligand binding. This may lead to differences in relative ΔG_bind of up to 75 kJ/mol when calculated with different approaches.

Many attempts have been made to explicitly include the effect of binding-site water molecules in MM/PBSA. Several groups have treated a number of water molecules as part of the receptor, often giving improved results [24,26,27,55], although the performance may depend on the number of explicit water molecules [56]. However, in a large test of 855 ligand complexes, inclusion of water molecules within 3.5 Å of the ligand made the results worse [57]. Attempts have also been made to combine MM/GBSA with estimates of the free-energy gain of displacing binding-site water molecules from the WaterMap approach with varying results [58-60]. We have tried to estimate both these effects in a consistent way within the MM/GBSA approach (by estimating the binding energy also of water molecules with MM/GBSA) with reasonable results [24].

6. The electrostatics term

E_el in Equation 55 is normally calculated using Coulomb’s law with atomic charges taken from the MM force field. Consequently, the results depend on the charges used for the receptor and the ligand. Several groups have studied how the results depend on the force field. Hou et al. tested different Amber force fields and obtained the best results with the 03 or 99 force fields, depending on the length of the MD simulations [33]. They also found that HF/6-31G* restrained electrostatic potential (RESP) charges for the ligand gave the best results, although AM1-BCC and ESP charges also gave satisfactory predictions. On the other hand, Oehme et al. obtained the best results with the simple Gasteiger and HF/STO-3G charges (which are small in magnitude), as well as the more sophisticated B3LYP/cc-pVTZ charges [44].

We have compared the results obtained with the Amber 94, 99 and 03 force fields, but did not find any significant differences [29]. We also calculated QM charges (HF/6-31G*) for all atoms in the protein and the ligand for the conformation observed in each snapshot of the MD simulations, but this did not improve the results. However, interaction energies calculated with such conformation-dependent charges strongly differ from those calculated by standard charges (by 40 kJ/mol on average for charged ligands), although the effect is partly cancelled by the solvation energy [61]. Moreover, if these charges were used for MD simulations, the calculations crashed with numerical problems. These problems could be avoided by averaging the QM charges over the snapshots or over all occurrences of the same amino acid in different proteins [61,62]. Such extensively averaged electrostatic potential (xAvESP) charges provide an alternative to standard RESP charges and actually gave slightly improved calculated ΔG_bind for two proteins. However, in another study, no significant differences between ΔG_bind calculated with AM1-BCC, RESP and xAvESP charges were observed [47].

In most force fields for proteins, polarization between different atoms is ignored, although it often constitutes 10 – 30% of the total electrostatic interaction energy [63]. We have tried to use a polarizable force field in MM/PBSA calculations, which increased the computational effort by a factor of ∼ 3, but no improvement in the results was observed [29]. We have also tested to use a very accurate force field consisting of multipoles up to quadrupoles and anisotropic polarizabilities, calculated for all atoms and bond centers in the actual conformation in all snapshots, but still with no improvement in ΔG_bind compared with experiments [52]. Ren et al. have combined the polarizable Amoeba force field with MM/PBSA, obtaining reasonable results [64].

In the original MM/PBSA approach, E_el was calculated with a dielectric constant of unity (ϵ = 1) [7,8]. However, it has frequently been suggested that the results may be improved by using a larger ϵ [16-18,65], which would also implicitly model some of the dielectric relaxation and dynamics of the ligand in the protein [66]. We have estimated the optimum value of the dielectric constant, obtaining varying results (ϵ = 1 – 25) depending on the solvation model and the protein [23]. Such varying results have also been observed in other studies and it has been suggested that the optimum value of ϵ depends on the characteristics of the binding site (a highly charged binding site requires a higher ϵ than a hydrophobic site) [17,67], but often the results are best for ϵ = 2 – 4 [14,15,52], especially in larger studies of several proteins [43,46]. Alternatively, it has been suggested that ϵ should vary with the protein residues [68].

7. The entropy term

In the original MM/PBSA approach [7,8], the entropy is calculated by removing all water molecules and residues > 8 Å from the ligand and then minimizing the remainder using a distance-dependent dielectric function. Vibrational frequencies are then calculated, which are used to obtain entropies by a normal-mode analysis using a rigid-rotor harmonic-oscillator ideal-gas approximation. A problem with this approach is that a third energy function is used (in addition to those used for the MD simulations and the calculations of the other energy terms) and that the receptor may relax in an uncontrolled way after the truncation of the protein. As a consequence, the entropy term typically gives the largest statistical uncertainty, as can be seen in Table 1.

Therefore, we suggested a simple modification of the protocol [69]: We included all residues and water molecules within 12 Å of the ligand in the minimization, but fixed the water molecules and residues between 8 and 12 Å in the minimization and ignored their contributions to the entropy. Thereby, we could use ϵ = 1 and avoid any large change in the structure. This led to a reduction of the uncertainty of the entropy term by a factor of 3, so that it no longer limited the precision. We have also shown that the calculated entropy depends little on the truncation radius and other parameters of the method and that 8 Å is a proper radius [70]. Another possibility to improve the precision of the entropy is to start the minimization of the free receptor and the free ligand from the minimized structure of the complex [71] or to perform the minimization in a GB solvent [72].

It is clear that the normal-mode entropies employed in MM/PBSA omit important contributions to the true ligand-binding entropy. In particular, it considers only the local stiffness of the actual binding conformation and does not include any information whether the receptor or the ligand may have many different conformations or whether the number of conformations changes upon binding. Likewise, the single-average approach omits possible changes in the conformation of the ligand or the receptor upon binding. In principle, it is possible to study different conformations of the receptor and the ligand in MD simulations and to calculate entropies from these, for example, from the dihedral distributions. Unfortunately, it is virtually impossible to obtain converged entropies from such simulations [73].

Several attempts have been made to replace the normal-model entropy in MM/PBSA with entropies calculated with other methods. For example, an entropic penalty has been assigned to rotable bonds in the ligand and in protein [74]. Other investigators have tested to calculate the entropy by a quasi-harmonic analysis of the MD trajectories [11,75], which includes the conformational part of the entropy, although not in a fully correct way [76], but also this approach has severe convergence problems [11]. A simpler approach based on the solvent-accessible and buried surface area has also been suggested and has been shown to perform as good as the normal-mode approach [45].

The entropy calculations typically dominate the computational cost of the MM/PBSA estimates. Therefore, it is sometimes calculated only for a subset of the snapshots [7,8,11]. It has also repeatedly been suggested that this term can be omitted and that it does not improve the results in large tests [26,43]. Consequently, this term is ignored in a large portion of the published MM/PBSA studies [16-18]. However, it is clear that for the absolute affinities, the entropy term is needed, owing to the loss of translational and rotational freedom when the ligand binds. Some studies have also indicated that the entropy term improves the results [19,44] or that it is enough to calculate the entropy of the ligand [77].

8. Replacing MM with QM

In contrast to the other terms in Equation 75 , we are not aware of any attempts to modify only the E_vdW term in MM/PBSA. However, it is well known that the MM energy model has several shortcomings and that a new force field (at least the charges) needs to be created for each new ligand studied [16]. Therefore, there has been a great interest to instead employ a quantum mechanical energy function [78].

Merz et al. pioneered this field by replacing the MM energies with a solvated semi-empirical QM (SQM) estimate, supplemented by a MM dispersion term and a simple entropy estimate [74]. Initially, they studied single snapshots, obtaining encouraging results for 165 protein–ligand complexes (r² = 0.55). This approach was subsequently extended to post-process MD snapshots of β-lactamase complexes, but the large standard deviation made the results of little use [79]. Recently, a similar approach was proposed, which gave better results than standard MM/PBSA on the Lck SH2 protein [80]. We performed a more systematic investigation of three SQM methods [81]. The results varied with the protein–ligand system, but it was clear that a dispersion correction is necessary to reproduce experimental affinities. On average, AM1 gave the best results, comparable to standard MM/GBSA, at a cost that was 1.3 – 1.6 times larger.

We also were the first to estimate binding affinities with a high-level QM method with large basis set for which dispersion and polarization are treated properly [52]. The calculations were done within an MM/PBSA framework, but the MM part was replaced with fragment MP2/cc-pVTZ QM calculations for all chemical groups within 4.5 Å of the ligand, treating many-body and long-range effects by a highly accurate force field that includes a multipole expansion up to quadrupoles and anisotropic polarizabilities at all atoms and bond centers [63], including PCM solvation. Unfortunately, the results were quite poor with r² = 0.20 – 0.52 depending on the G_np term. The results also showed that three-body effects (mainly the coupling between polarization and repulsion) absent in any standard MM representation (also polarizable) affect receptor–ligand interactions by 2 – 10 kJ/mol [63].

Furthermore, various QM/MM-PBSA approaches have been developed, in which the ligand is treated with QM and the rest with MM [82-84]. We used this approach to estimate binding of ligands to cathepsin B, but found that QM/MM-PBSA energies (r² = 0.59) were worse than gas-phase QM energies (r² = 0.80) [85]. However more recently, accurate QM/MM-PBSA results have been obtained for cytochrome P450 [86], showing that performance depends on the system.

Skylaris et al. have recently applied linear-scaling density functional theory (DFT) calculations to ligand binding, treating the whole protein–ligand complex [87,88]. They obtained a MAD of 9 kJ/mol, which is slightly better than the MM/PBSA result, but the ranking was poor. Other groups have used similar methods on rather large host–guest systems [89,90].

The use of QM calculations exaggerates the inconsistency between the energy functions used for sampling and post-processing. Some studies try to solve this by performing a QM minimization before the energy evaluation [79,80,91], but our study indicates this hardly corrects the ensemble mismatch [30]. A better solution would be to do the MD simulation also at the QM level as has been done at the SQM level [92].

9. Comparison with other methods

It is of great interest to compare the performance of MM/PBSA and other alternative methods. LIE and MM/PBSA have been compared several times, but the results depend on the tested system [47,56,93-98]. MM/PBSA often overestimates differences in binding affinities, giving a favorable r², but a poor MAD [99]. We have instead compared the efficiency and precision of LIE and MM/PBSA, showing that LIE is two to seven times more efficient than MM/PBSA, owing to the time-consuming entropy estimate [100].

Schutz and Warshel compared the PDLD/s-LRA/β, LIE and MM/PBSA methods, concluding that the former was most accurate [66]. However, they only compared with selected literature values for MM/PBSA, which may introduce biases from differences in the force field, simulation set-up and continuum model. Therefore, we performed a study where all such differences were removed for two proteins [23]. Although LRA is theoretically the more strict approach, our results indicated that standard MM/PBSA is more accurate, more precise and also less computationally demanding. For avidin, LIE outperformed MM/PBSA for the non-polar contributions, but this was not the case for fXa.

It is also of interest to compare MM/PBSA with the more strict AP methods. We performed such a comparison for nine inhibitors of fXa [99]. It was found that the two methods gave similar MAD, but AP gave a better r² compared with experiments. Interestingly, we also found that an optimized AP approach actually was more efficient than MM/PBSA contrary to common belief [17]. This was mainly due to that MM/PBSA is inherently imprecise, so that many independent simulations are needed to give a precision similar to that of AP. On the other hand, the optimization of the AP approach has been shown to be system-dependent [101]. Other studies have mainly focused on the accuracy and have found that MM/PBSA is comparable [102,103], inferior [25,104,105] and better [106] than AP, depending on the system.

10. Conclusions

We have presented an overview of the MM/PBSA method to predict ligand-binding affinities. The method contains six energy terms that can be individually tested and improved. In separate sections, we have discussed most of these terms.

The electrostatic term depends on the charges used for the receptor and the ligand, and several attempts have been made to improve these by polarizable potentials, multipole expansions or QM calculations, but with little improvement in ΔG_bind. It also depends on the dielectric constant used for the protein and there are some indications that the results can be improved by using ϵ = 2 – 4, especially for polar and charged binding sites.

The polar solvation term often partly cancels E_el. It was originally calculated by PB, but today most studies are performed with GB solvation, which is faster and often gives a better accuracy. However, the results are very sensitive to details in the calculations and different GB methods give widely different results. The non-polar energy has been less investigated, but recent studies indicate that any continuum estimate may be inaccurate owing to lack of information about water molecules in the binding site.

The normal-mode entropy is also problematic, because it is expensive to calculate and it lacks information of the conformational entropy. Unfortunately, alternative methods do not give converged results. Therefore, the term is often omitted.

Many approaches have been suggested to replace the MM force field with QM calculations for the ligand or for the whole complex, for example, by using SQM, DFT or ab initio methods. So far, the results have been varying and the inconsistency between energy function used for simulations and energy calculations is a potential problem.

Traditionally, MM/PBSA energies are calculated for snapshots obtained by MD simulations. Unfortunately, there is a very large variation in these energies, giving major problems with the precision. These are normally solved by calculating only interaction energies (Equation 75 ), studying many snapshots and using several independent simulations. It has frequently suggested that the calculations can be sped up by using only minimized structure, but such results may depend strongly on the starting structures.

Finally, MM/PBSA has been compared with other ligand-binding methods, with varying results. Typically, the accuracy is better than for docking and scoring methods, worse than for AP methods and comparable to other end point methods, such as LIE and LRA.

11. Expert opinion

MM/PBSA is a popular method to calculate absolute binding affinities with a modest computational effort. Originally, it was presented as a method that does not contain any adjustable parameters and consists of six well-defined terms. However, since then many variants have been suggested and the user now have to make many choices, for example, concerning the dielectric constant, parameters for the non-polar energy, the radii used for the PB or GB calculations, whether to include the entropy term and whether to perform MD simulations or minimizations. In practice, it typically gives results of intermediate quality, often better than docking and scoring, but worse than FEP, for example, r² = 0.3 for the whole PDB bind database, but r² = 0.0 – 0.8 for individual proteins [46]. The ranking of ligands is often unsatisfactory if their affinities differ by < 12 kJ/mol [18]. As for most ligand-binding approaches, the results depend critically on the tested receptor–ligand system, but it allows for larger variation in the ligand scaffold than AP methods and is less sensitive to changes in the net charge.

Unfortunately, the results strongly depend on the continuum solvation employed, making the absolute affinities unreliable or the method empirical (the solvation method can be selected to give accurate ΔG_bind). The dielectric constant and whether to include the entropy term has also become parameters that can be varied to improve the results.

Undoubtedly, the method involves severe thermodynamic approximations [11,22,54], for example, ignoring structural changes in the receptor and ligand upon binding and conformational entropy, and lacking information about the number and entropy of water molecules in the binding site before and after ligand binding. Moreover, no attempt to improve the approach by using more accurate methods, for example, involving QM calculations, 3D-RISM solvation, polarizable force fields or more detailed non-polar energies, has given any consistent improvement. Instead, the best results are often obtained with methods that give numerically small energies.

MM/PBSA has severe convergence problems, requiring many independent simulations to yield a useful precision (thereby reducing its advantage compared with computer intensive methods like AP). All results (including quality measures like r² or MAD) should be accompanied by an estimate of the statistical precision and any comparison of ligands or methods must take this uncertainty into account in a statistically valid way. MM/PBSA typically gives too large energies, thereby often giving a good r² but a poor MAD (often worse than the null hypothesis of the same affinity for all ligands).

In conclusion, MM/PBSA may be useful for post-processing of docked structures or to rationalize observed differences. However, it is not accurate enough for predictive drug design or as a basis to develop more accurate methods.

Article highlights.

• The MM/PBSA and MM/GBSA (molecular mechanics energies combined with the Poisson–Boltzmann or generalized Born and surface area continuum solvation) methods have been used to estimate ligand-binding affinities in many systems, giving correlation coefficients compared with experiments of r² = 0.0 – 0.9, depending on the protein.

• The results strongly depend on details in the method, especially the continuum-solvation method, the charges, the dielectric constant, the sampling method and the entropies. The methods often overestimate differences between sets of ligands.

• Many attempts have been made to improve the results, for example, by using various tastes of quantum mechanics (QM) methods, QM charges, QM solvation, three-dimensional reference site interaction model solvation, polarizable force field, multipole expansions or more detailed estimates of the non-polar energies. However, this has not led to any consistently improved results.

• The methods involve several severe approximations, for example, a questionable entropy, lacking the conformational contribution and missing effects from binding-site water molecules.

• Consequently, the methods may be useful to improve the results of docking and virtual screening or to understand observed affinities and trends. However, they are not accurate enough for later states of predictive drug design.

Declaration of interest

U Ryde is supported by a grant from the Swedish research council (project 2010-5025) and the Swedish National Infrastructure for Computing (SNIC), while S Genheden is supported by a grant from the Wenner-Gren Foundations. The computations were performed on computer resources provided by SNIC at Lunarc Lund University, HPC2N at Umeå University, and C3S3 at Chalmers Technical University. The authors have no other relevant affiliations or financial involvement with any organization or entity with a financial interest in or financial conflict with the subject matter or materials discussed in the manuscript apart from those disclosed.

Notes

This box summarizes key points contained in the article.