Stochastic exit from mitosis in budding yeast

Abstract

Unlike many mutants that are completely viable or inviable, the CLB2-dbΔ clb5Δ mutant of Saccharomyces cerevisiae is inviable in glucose but partially viable on slower growth media such as raffinose. On raffinose, the mutant cells can bud and divide but in each cycle there is a chance that a cell will fail to divide (telophase arrest), causing it to exit the cell cycle. This effect gives rise to a stochastic phenotype that cannot be explained by a deterministic model. We measure the inter-bud times of wild type and mutant cells growing on raffinose and compute statistics and distributions to characterize the mutant’s behavior. We convert a detailed deterministic model of the budding yeast cell cycle to a stochastic model and determine the extent to which it captures the stochastic phenotype of the mutant strain. Predictions of the mathematical model are in reasonable agreement with our experimental data and suggest directions for improving the model. Ultimately, the ability to accurately model stochastic phenotypes may prove critical to understanding disease and therapeutic interventions in higher eukaryotes.

Introduction

Normally, the progression of eukaryotic cells through the DNA replication-division cycle is extremely robust to alterations in growth conditions, exposure to damaging radiation, stochastic fluctuations of protein levels within the cell and other vicissitudes of life. Mutant cells, on the other hand, in which critical parts of the cell cycle control system are compromised, may be much more sensitive to their environment than normal cells. Cancer cells, for instance, are notoriously non-robust: they grow and divide in a deregulated fashion, they exhibit aberrant mitotic cycles, and they rapidly accumulate genetic mutations.1 An interesting example of this sort of fragility of the cell cycle has been observed in mutant strains of budding yeast (Saccharomyces cerevisiae). Wild-type cells grow and divide on a variety of carbon sources: growing rapidly on glucose (mass doubling time, MDT ≈ 90 min), less rapidly on other sugars (e.g., MDT ≈ 150 min on raffinose) and poorly on ethanol.2 In all cases, the number doubling time (NDT) of the culture is nearly identical to the MDT, and very few cells exit the cell cycle. (Yeast cells age and eventually stop dividing after 15–25 generations.3) Most cell cycle mutants of budding yeast are either inviable (i.e., fail to proliferate) or viable but somehow abnormal (e.g., smaller or larger than wild-type cells). Some rare mutants, however, exhibit an unusual phenotype: they are inviable on glucose but partially viable on sugars, like raffinose, that support a slower growth rate. For example, the double mutant strain, CLB2-dbΔ clb5Δ, which has the destruction box region of the CLB2 gene and the entire CLB5 gene deleted, is inviable on glucose but forms small colonies on galactose.4,5 The goal of this paper is to characterize in detail the effects of these genetic mutations on the cell cycle control system in budding yeast by quantitative measurements of growth of this mutant strain in raffinose and by comparison to computer simulations of a stochastic model of the molecular control system. Conceptually, our work is related to a recent study wherein a stochastic, mechanistic model was used to explain the temporal variability of cell cycle entry in wild-type mammalian cells.6

In our case, the CLB2-dbΔ clb5Δ mutant strain is compromised at the stage of exit from mitosis. The B-type cyclins, Clb5 and Clb2 (encoded by the genes CLB5 and CLB2), when complexed with Cdc28 (the cyclin-dependent kinase), play crucial roles in driving DNA synthesis and mitosis during the budding yeast cell cycle.7 Towards the end of the mitotic cycle (metaphase), a yeast cell has copious amounts of Clb2 and Clb5Δ For the cell to exit mitosis and return to the G₁ phase of the next cycle, the activities of the Cdc28:Clb2 and Cdc28:Clb5 complexes must be abolished, which is accomplished by degradation of Clb2 and Clb5 proteins and by production of an inhibitor, Sic1, of Cdc28:Clb complexes. An E3-ubiquitin ligase, called the Anaphase Promoting Complex (APC), is responsible for polyubiquitination of Clb2, Clb5 and other proteins, thus labeling them for degradation by 20S proteasomes.8 Figure 1 diagrams the relevant interactions for this aspect of the cell cycle. In the figure and in our model we combine redundant cyclins, so that Clb2 stands for Clb1 as well as Clb2, and Clb5 stands for Clb5 as well as Clb6. In addition, since Cdc28 is present in excess and combines rapidly with cyclins once they are synthesized, we assume all cyclin molecules have a Cdc28 partner.

The APC requires an auxiliary protein (either Cdc20 or Cdh1) to recognize particular proteins for poly-ubiquitination, and this recognition depends on a specific short sequence in the targeted protein.8,9 All known APC:Cdc20 substrates contain a destruction box (D-box) composed of the sequence R-X-X-L-X-X-X-X-N, whereas APC:Cdh1 recognizes both the D-box and another short sequence composed of K-E-N (the KEN box). Clb2 is degraded by both APC:Cdc20 and APC:Cdh1, while Clb5 is degraded mainly by APC:Cdc20.10–13 When the destruction box sequence is deleted from the CLB2 gene (CLB2-dbΔ), the mutant protein retains its wild-type function as a B-type cyclin but it cannot be degraded by APC:Cdc20, and the ability of APC:Cdh1 to degrade it is also compromised to a large extent.4,10 Moreover, APC:Cdh1 is strongly inhibited by Clb5-dependent phosphorylation. The single mutant CLB2-dbΔ is stuck in telophase, unable to divide, because it cannot downregulate Clb2:Cdc28 activity to a sufficiently low level.4 This strain, however, can be partially rescued by deleting the gene that encodes Clb5 (CLB2-dbΔ clb5Δ).4,5 Although the double mutant cell has an excess of Clb2 in telophase, it has no Clb5 and this combination of abnormalities suffices to allow some cells to exit mitosis, return to G₁ and commence a new cell cycle, provided the cells are growing slowly on a non-preferred sugar like raffinose.

In order to maintain the double mutant strain in the laboratory, a third mutation is introduced: CLB2-dbΔ clb5Δ GAL-SIC1, which adds a copy of the SIC1 gene under the control of the galactose promoter. When grown on galactose, Sic1 (a stoichiometric inhibitor of Cdc28:Clb2) is produced constitutively, which grants the mutant strain full viability. When the strain is transferred to glucose medium, it dies; and when transferred to raffinose medium, it survives although just barely.

As interesting as this mutant is to our understanding of cell cycle control, it has not been much studied either experimentally or theoretically. Chen et al. proposed a computer model of the cyclin-dependent kinase regulatory network in budding yeast and showed that their deterministic model (based on non-linear ordinary differential equations) can account in quantitative detail for the phenotypes of 120 different mutant strains.14 Nonetheless, their model could not give a satisfactory explanation of CLB2-dbΔ clb5Δ GAL-SIC1. Simulations of this strain showed viability in galactose and inviability in glucose, as they should, but for raffinose the simulation indicated full viability rather than partial viability. The reason for this discrepancy, of course, is that a deterministic model cannot possibly predict partial viability, which is a reflection of the fact that in telophase some of the mutant cells successfully exit mitosis and enter a new cell cycle, whereas other cells get stuck in telophase and never divide again. To account for such behavior, we need to transform Chen's 2004 model into a realistic stochastic model accounting for molecular noise in the cyclin-dependent kinase regulatory network. Furthermore, to judge the accuracy of the model, we need to collect quantitative data on the proliferation of CLB2-dbΔ clb5Δ GAL-SIC1 cells on raffinose, especially statistics on how often cells leave the cycle never to divide again.

In this paper we examine the proliferation on raffinose medium of wild-type and triple-mutant (CLB2-dbΔ clb5Δ GAL-SIC1) cells by time-lapse photomicroscopy and compute relevant statistics from these observations. In addition, we convert Chen's model into a form suitable for stochastic simulation by Gillespie's method,15,16 and compute the same statistical properties of simulated cell populations. We show that the model and the experiments are in reasonably good accord.

The development of stochastic models to capture the behavior of molecular regulatory networks in single cells is becoming increasingly important as data on protein and mRNA distributions are now routinely collected from single cells by techniques based on fluorescence microscopy.17–25 Because cellular processes are inherently stochastic, this single-cell data cannot be fit by deterministic models. In many cases, to be sure, the data is only slightly noisy and deterministic models may provide an adequate interpretation of the mean of the distributions. But in other cases, as in this paper, molecular noise has significant, qualitatively different effects on cell fate that can only be captured adequately with a stochastic model. Many important questions in medicine may hinge on the fraction of cells that undergo a certain fate; for example, the fraction of cancer cells that undergo apoptosis in response to drug therapy. Hence, the combination of experimental and stochastic-modeling studies presented here is important as an initial step along the road to understanding the stochastic character of cell regulation in normal cells, and how it is altered in diseased states and in therapeutic interventions.

Results

We recorded the rates of cell growth and proliferation of wild-type and mutant cells growing on raffinose agar and observed by time-lapse, phase-contrast microscopy. Because it is easier to determine the time of bud initiation than the time of cell division (when mother and daughter cells separate), we used interbud intervals to measure cell cycle times. By T_bMb we denote the time between successive budding events of a mother cell (a cell that has already budded at least once), and by T_bDb we denote the time from a daughter cell's first appearance as a bud from a mother cell to the time when the daughter cell produces her first bud. More traditionally, the cycle time of a mother cell would be defined as T_M, the time from one cell division to the next. With reference to Figure 2, we see that T_M = T_dMb + T′_bMd, where T_dMb is the time from cell division to the next budding event in a mother cell and T′_bMd is the time from budding to the next division in a mother cell. Also, T_bMb = T_bMd + T_dMb. Since the means of T_bMd and T′_bMd are the same, the means of T_M and T_bMb are equal. The variances of T_M and T_bMb may not be the same since the covariance of T_dMb and T′_bMd, and the covariance of T_dMb and T_bMd, could be different. We expect these covariances to be small, since the time intervals are relatively independent of one another, and so the variances of T_M and T_bMb will be almost equal. Similar arguments show that the cycle time of a daughter cell, T_D = T_dDb + T_bDd and T_bDb = T_bMd + T_dDb will have the same means and similar variances.

We employed several indicators of cell growth and division to compare wild-type and mutant cells growing on raffinose. We used growth curves (i.e., logarithm of the total number of budding events versus time) to compute NDT (number doubling time) and quantify how fast the cells are proliferating. To determine whether differences in NDT are due to slower cellular growth rates or to cells exiting the cell cycle, we have plotted the cumulative distribution function of cell cycle time, e.g., P_M(T) = Probability{T_bMb > T}. Dendrographs were used to provide a time-domain view of the regularity or irregularity of budding events, while histograms were used to quantify the distributions of interbud times in populations of mother cells and daughter cells.

Wild-type cells.

Wild-type yeast cells grow well in both glucose and raffinose, but we confine our results to raffinose to allow comparison with the mutant cells growing in raffinose. In three separate experiments we recorded the budding times during proliferation of a small number of initial cells. Figure 3A presents the growth data along with the least squares fits that were used to compute NDT. As reported in Table 1, NDTs for wild-type cells growing on raffinose ranged from 120 minutes to 155 minutes. Table 1 also records the statistics for T_bMb and T_bDb. As expected, the mean of T_bDb (cycle time of daughter) is greater than the mean of T_bMb (cycle time of mother), since T_dDb > T_dMb. (After cell division, the daughter cell is smaller than the mother cell, and therefore the daughter takes longer, on average, than the mother cell to reach the size threshold to initiate the next budding event). This difference is much more pronounced in experiments 1 and 3 than in experiment 2. The distributions of T_bMb and T_bDb (Fig. 4A–C) overlapped significantly in all cases.

To determine whether the wild-type NDT is significantly affected by cells exiting the cell cycle, we estimated the probability, P(T), that the cycle time is greater than a specified time, T, as shown in Figure 3B. If a fraction of cells had exited the cell cycle, then P would level off at an asymptotic value, P_∞, as T gets large, but there is no evidence, for wild-type cells, from Figure 3B that P is reaching an asymptotic value for large T. With an experimental time window of only 10 hours, it is difficult to get a good estimate of the tail of the P(T) distribution; but, if wild-type cells are exiting the cell cycle, then the fraction is much less than 10%.

Our conclusion that wild-type cells divide slowly but consistently on raffinose medium is born out by dendrographs of cell genealogies derived from time-lapse micrography. Figure 5A shows three representative wild-type lineages. Each dendrograph shows one cell and its progeny over a viewing window of 600 min. Examining dendrographs of all regions observed in experiment 1, we could find only a few wild-type cells that possibly exited the cell cycle.

CLB2-dbΔ clb5Δ mutant.

As expected, the mutant cell populations exhibited a longer NDT than that observed for wild-type cells; slightly longer in the first experiment and almost double in the second and third experiments (see Table 1 and Fig. 3A). There are two possible causes for this increase, which are not mutually exclusive: (1) the mutant cells may have grown more slowly than wild-type cells on raffinose and therefore had a longer cell cycle time in general or (2) a greater number of the mutant cells may have exited the cell cycle and eventually died. Our data suggest that the dominant cause of the increased NDT is the greater number of mutant cells exiting the cell cycle. For instance, while in experiments 2 and 3 the NDT of mutant cells is much longer than the NDT of wild-type cells (longer by 176 and 85 minutes, respectively), the mean interbud times of the mutant cells are only about 30 minutes longer than the mean interbud times of the wild-type cells. Hence, mutant cells that are able to divide and rebud are growing only marginally slower than wild-type cells, so the large increase in NDT must be attributed to cells that are permanently arrested in the cell cycle and are no longer contributing to an increase in cell number.

Figure 3B, where we plot the cumulative probability, P(T), that mutant cell cycle time > T, shows clearly that a significant fraction of the mutant cell population had exited the cell cycle (P_∞ may be as large as 25—40% in the three experiments). The three dendrographs in Figure 5B provide further evidence for this conclusion. In the lowest dendrograph, the cells bud regularly with roughly equal mother and daughter interbud intervals. In the middle dendrograph, the cell never buds over the course of 10 h, while in the upper dendrograph each cell buds once and never again. This very erratic behavior caused the standard deviation of mutant cell cycle times to be much greater than that of wild-type cells (see Table 1).

The histograms of cycle times for mother and daughter cells (Fig. 4E–G) show considerable overlap, i.e., the means and variances of T_bMb and T_bDb were roughly equivalent (see Table 1). Furthermore, the cycle time histograms for mutant cells (Fig. 4E–G) exhibited much longer tails than the histograms for wild-type cells (Fig. 4A–C), probably due to the difficulties of some cells in exiting mitosis.

The preponderance of evidence indicates that, although CLB2-dbΔ clb5Δ mutant cells can produce colonies on raffinose, the NDT of mutant colonies is much longer than the NDT of wild-type colonies on the same growth medium largely because a significant fraction of mutant cells leave the cell cycle, never again to rebud.

Simulation results.

The mathematical model that we used to simulate these experiments was based on a deterministic model (ordinary differential equations, ODEs) of the budding yeast cell cycle developed by Chen et al. Before describing the changes we made to incorporate stochastic events in the Chen-2004 model, we first summarize relevant features of the deterministic model. An important input parameter to the deterministic model is µ, the specific growth rate of the cells (µ = ln2/MDT, where MDT is the mass doubling time of the culture). For growth on glucose medium, µ = 0.0077 min⁻¹ (MDT = 90 min), and for raffinose medium, µ = 0.00433 min⁻¹ (MDT = 160 min). All other parameters in the model are rate constants and binding constants for the biochemical reactions describing the complex network of molecular interactions that govern the temporal activity patterns of cyclin-dependent kinases (the enzymes that control the timing of DNA synthesis, mitosis and cell division in yeast—and all other eukaryotes). Chen et al. defined a ‘basal’ set of values for these parameters,14 corresponding to the situation in wild-type cells, which we have slightly modified (see Methods). If the ODEs are simulated deterministically for that basal parameter set with µ = 0.0077 min⁻¹ (or 0.0043 min⁻¹), then the simulated population of mother and daughter cells will undergo exponential expansion with NDT = 90 min (or 160 min), matching experimental observations that wild-type cells proliferate exponentially in both glucose and raffinose media, with little evidence of cell senescence or death. Furthermore, for wild-type cells growing in nutrient media with any value of µ smaller than about 0.01 min⁻¹, cell number expands exponentially with NDT = MDT (“balanced growth and division”). For µ > 0.01 min⁻¹ (MDT < 69 min), daughter cells grow faster than they can replicate their DNA and divide, so cells get larger and larger each generation and eventually die. This property of the model is in accord with the maximum specific growth rate (∼70 min) observed for budding yeast.26

To simulate the CLB2-dbΔ clb5Δ mutant strain we made three changes to the basal parameter set of the Chen-2004 model: the rate constant kdb2p, associated with the degradation of Clb2 by APC:Cdc20, was set to 0 and the rate constant kdb2pp, associated with the degradation of Clb2 by APC:Cdh1, was set to 0.075 times the wild-type value to account for the destruction box deletion; and the rate constants ksb5 and ksb5pp, associated with the synthesis of Clb5 were set to 10% of the corresponding wild-type values to reflect that Clb6 is still intact in this mutant. (Recall that ‘Clb5’ in our model combines the contributions of both Clb5 and Clb6 proteins in a cell). Deterministic simulations of Chen et al. for newborn cells demonstrated that the mutant strain is inviable (arrested in telophase) for any MDT < 139 min,14 in agreement with the observation that the mutant strain is inviable on glucose medium. For any MDT >139 min, deterministic simulations of the Chen-2004 model showed the newborn mutants to be perfectly viable. (It should be noted that the MDT threshold depends somewhat on the initial conditions assumed for the cells being simulated and has a fairly strong dependence on the initial mass). The reason for this difference in viability is that the ability of a cell to exit mitosis depends critically on the level of Clb2 present when the spindle assembly checkpoint is lifted and Cdc20 becomes active. The synthesis of Clb2 in our model depends upon the cell mass, so, for a given initial cell mass, a faster growth rate creates a higher level of Clb2 when Cdc20 becomes active. If the growth rate is sufficiently large, the resulting level of Clb2 will be so high that the cell cannot exit mitosis.

The abrupt change in viability of the mutant strain at MDT = 139 min is not consistent with our experimental observations of how the mutant strain proliferates in raffinose medium. In actuality, the cells successfully complete the cell cycle most of the time, but in each pass through the cell cycle there is apparently a finite probability that a cell will arrest in telophase and never bud again. We supposed, following a suggestion in Chen et al. that this behavior is attributable to random fluctuations in the cell cycle control network, and we set out to create a reasonable stochastic version of the Chen-2004 model that might shed light on the behavior of the CLB2-dbΔ clb5Δ mutant strain growing on raffinose.

There are several alternatives for converting a deterministic (ODE) model into a stochastic model.15,16,27–34 We chose to use Gillespie's algorithm,15,16 which treats every reaction rate in the deterministic model as a ‘propensity’ for that particular reaction to occur. From the numerical values of these propensities, Gillespie's algorithm determines when the next reaction will occur and which (of the ∼100 reactions in Chen's model) it will be. Strictly speaking, Gillespie's algorithm applies only to elementary reaction mechanisms, but it is a common approximation among systems biologists to apply the algorithm to non-elementary reaction mechanisms, like the Michaelis-Menten kinetics in the Chen-2004 model.35–37 Recent research has justified the extension of Gillespie's algorithm to Michaelis-Menten kinetics under some circumstances.38–41 On the contrary, other recent research42,43 suggests that the deterministic cell cycle models developed by Tyson & Novak44 and by Chen et al. are not really suitable for stochastic simulation by this simple extension of Gillespie's algorithm. Nonetheless, Mura & Csikasz-Nagy have created a stochastic version of the Tyson-Novak-2002 model by reinterpreting reaction rate laws as reaction propensities in the sense of Gillespie's algorithm,45 and we have done the same for the Chen-2004 model. We consider this stochastic interpretation of the Chen-2004 model as a “first approximation” to effects of molecular noise in the cell cycle control system of budding yeast.

To determine the molecular abundances of each species used in the stochastic model, we must estimate the “characteristic concentration” of each dimensionless variable in the Chen-2004 model and specify the average volume of a yeast cell. (The normalized concentration used in the model is defined as the actual concentration divided by the characteristic concentration). Mura & Csikasz-Nagy chose a constant, average “compartment” volume of 0.84 fL (a yeast cell nucleus) and used the same characteristic concentration of 1 µM for every variable in the Tyson-Novak-2002 model.45 They recognized the limitations of this assumption and left to “future modeling work the goal of a more accurate representation of the abundances of species.” To this end, we assumed different characteristic concentrations for each species (see Table 3) in order to align our species abundances with experimental measurements.19 Like Mura & Csikasz-Nagy, we chose a constant, average “compartment” volume; in our case, V = 30 fL, which is roughly the size of a yeast cell.46 Our characteristic concentrations are about 30-fold smaller than Mura and Csikasz-Nagy's and our compartment volume is about 30-fold larger, so the total number of molecules per reactor volume is comparable in the two models. Our model is more detailed than Mura and Csikasz-Nagy's (which is necessary in order to simulate the CLB2-dbΔ clb5Δ mutant), and our estimates of the relative numbers of the different molecular species are more realistic than theirs.

The Chen-2004 model contains a parameter (f) that determines the fraction of a dividing cell's volume that is partitioned to the daughter cell. This parameter determines, in large measure, the difference between cycle times of mother and daughter cells. From our observations that this difference is small in raffi-nose (see Table 1), we estimate that f = 0.48, and this is the value we have used in our stochastic simulations.

Since the Chen-2004 model does not contain a detailed molecular mechanism for the budding event, we use the time between divisions to compute the relevant statistics for the simulations. As argued in the introduction to the results, the interdivision times and interbud times should have the same means and similar variances, so the quantities we are computing from experiments and simulations are comparable.

Simulation results (for the case: MDT = 160 min, V = 30 fL) are summarized in Table 1 and in Figures 2–4. The NDT for simulated wild-type cells is ∼160 min, as expected given our choice of growth rate. For simulated mutant cells, the NDT is 322 min, which is slightly higher than the longest experimental value. That the mutant NDT is significantly greater than the interdivision times of the mothers and daughters is due to cells exiting the cell cycle and ceasing to replicate. The cumulative distribution functions in Figure 3B show that the wild-type cells never exit the cell cycle, whereas over 40% of the mutant cells exit the cell cycle. The simulated distribution of the mutant cells in raffinose (black dashed line in Fig. 3B) compares favorably with the distributions observed experimentally.

From Table 1 we see that, in accord with the experimental results, the standard deviations of the statistics for our simulations increase by a factor of about two between the wild-type and mutant cases. On the other hand, the values of the standard deviations are about half those measured in the experiment. This lower noise level of simulation as compared to experiments can also be seen from the cumulative distribution functions in Figure 3B. For a deterministic simulation, the distribution functions would have no rounded corners and would drop vertically from a probability of 1 to a probability of 0. The rounded corners and non-vertical slopes are due to the effects of stochastic fluctuations of proteins on progression through the cell cycle. The roundness of the corners is greater and the slopes less steep for the experimental results, indicating significantly more noise in the experiments than in the simulations. The lower noise level in the simulation can also be seen by comparing Figure 4H to E–G. The simulated histogram of interdivision times shows a very quick drop towards zero after 200 minutes, whereas the experimental histograms show much heavier tails.

The dendrograph for simulated mutant cells (Fig. 5D) shows that while the original mutant cell divides once and then appears to exit the cell cycle, the daughter cell and its progeny divide fairly regularly. The overall high probability of not dividing, as seen in Figure 3B, appears to be due mainly to the many cells in the simulation that never divide at all.

The noise in our simulations can be increased by decreasing the average cell volume used in the simulations from 30fL to 15fL, hence halving the average number of molecules per cell. The result, seen in Table 1, is that the mean division times stay about the same while the standard deviations increase significantly, as expected. In addition, fewer cells exit the cell cycle and so the NDT decreases into the range seen in the experiments.

We can also look at the effect of decreasing the MDT of the simulation from 160 minutes to 150 minutes. Table 1 shows, as expected, that the mean division times decrease to reflect the new MDT while the standard deviations remain about the same. The number of cells exiting the cell cycle increases (i.e., NDT increases significantly) because we are nearer to the deterministic MDT survival limit.

Although we did not simulate the case where the mutant cells grow more slowly than the wild-type cells, it is straightforward to see what would happen. If the wild-type cells are allowed to grow somewhat faster by decreasing their MDT, the NDT of the wild-type would decrease to track the new MDT, and the net result would simply be an increase in the difference between the wildtype and mutant NDTs. This would not change the fact that the main reason for the difference in NDTs is the larger number of mutants exiting the cell cycle.

Discussion

Mutant strains are routinely used to unravel the operation of regulatory networks in normal and diseased cells. From the perspective of a mathematical modeler, mutant phenotypes provide constraints on both the structure of the model and the numerical values attributed to its parameters (rate constants). Even a very complex regulatory system, such as the cyclin-dependent kinase network in budding yeast, can be effectively modeled if data are collected from a wide range of mutants that impact all aspects of the control system.14 Especially useful in this regard are mutations that induce unusual phenotypes, such as the stochastic-survival phenotype of the CLB2-dbΔ clb5Δ mutant considered in this paper. From observations of single cells, we have measured the statistical properties of cell cycle progression in populations of wild-type and mutant cells growing on raffinose medium. These statistical measurements are used to test the best current model of the budding yeast cell cycle,14 as well as to provide constraints on future modeling efforts.

In the deterministic model on which our work is based, the stochastic phenotype was rationalized by choosing parameters such that mutant cells are inviable at fast growth rates (µ > µ_crit) and viable at sufficiently slow growth rates (µ < µ_crit). The boundary between viability and inviability of mutant cells depends on the relative amounts of Clb2 and Sic1 in telophase. If Clb2-dependent kinase activity is not too large in telophase, then Sic1 can rapidly accumulate, bind to and inhibit Cdc28:Clb2 and drive the cell into G₁ phase. But if a telophase cell has a little too much Clb2-dependent kinase activity, then Sic1 cannot make a comeback and the cell arrests in telophase. Because Clb2 synthesis in the model depends on cell size, mutant cells that are growing more rapidly or that are exceptionally large at birth will have so much Clb2 protein at the end of the cell cycle that they arrest in telophase. Mutant cells that are growing more slowly or are smaller at birth, will have less Clb2 protein at the end of the cell cycle and a greater chance of dividing and returning to G₁. This intuitive explanation of the mutant phenotype captures the basic mechanism, but in the full model there are many interacting feedback loops that govern exit from mitosis and therefore many ways in which fluctuations of protein levels can influence the transition. A satisfactory explanation of the mutant phenotype requires an appropriate stochastic version of the model.

In order to perform stochastic simulations of the deterministic model of Chen et al.14 which is formulated in terms of dimensionless concentration variables, it must be converted into variables that reflect the true numbers of molecules of regulatory proteins in a yeast cell (see Methods). Treating the phenomenological rate laws of the Chen-2004 model as reaction propensities, we simulated molecular fluctuations in the regulatory network by Gillespie's stochastic simulation algorithm.16 This approach allows for straightforward conversion of a deterministic model to a stochastic version,45 but it is subject to some uncertainties.42 As a first step to explore the stochastic phenotype of CLB2-dbΔ clb5Δ mutant cells, we opted for the simplified approach. More accurate and reliable models, based on multisite phosphorylation mechanisms that are perfectly suitable for stochastic simulation by Gillespie's algorithm, are currently under development.47,48

Analysis of stochasticity in gene expression in yeast has shown that the dominant component of noise is extrinsic as opposed to intrinsic in character.49 While using Gillespie's algorithm to simulate the progress of individual reactions in our model helps to account for the intrinsic noise, it does not directly account for extrinsic noise. However, two of the major sources of extrinsic noise are the growth and division of cells, and the existence of common upstream regulators whose intrinsic variation is passed on to regulated genes as an extrinsic variation.50 Since our model explicitly accounts for increasing cell mass, non-uniform cell mass at division, and the effect of upstream regulators on downstream targets, we are including some of the major sources of extrinsic noise.

The standard deviation of inter-division times that we compute from our model is only one-half the value we have measured experimentally, suggesting that noise levels in our simulations are too low. Probably the biggest reason for underestimating noise levels is that our model does not include mRNAs explicitly (as they were not a part of the Chen-2004 deterministic model), and therefore we are only modeling protein noise. Previous work with a highly simplified cell cycle model has shown that noise introduced by the small numbers of mRNA molecules in yeast cells may be the dominant source of intrinsic noise in cells.43 Thus, future models will need to incorporate the effects of small abundances of mRNAs on protein variation, although how to realistically capture this complicated process in a simple manner is the object of ongoing research.51

Comparison of the cumulative distribution functions of cycle times (Fig. 3B) shows that our simulations somewhat overestimate the number of mutant cells that exit the cell cycle. As mentioned, this is because a larger proportion of cells never divide at all in the simulation as compared to the experiments. Examination of the underlying deterministic model shows that cells with small initial mass divide whereas those with large initial mass do not. Because the fate of a cell in the deterministic model is so intimately tied to its birth mass, we were careful in specifying the initial conditions for our simulation of mutant cell populations (see Methods). Nonetheless, many of these cells are evidently too large to divide within the context of our current model, even with the help of molecular noise. Future models will need to look more closely at the coupling of cell cycle progression to cell growth.

In summary, we have experimentally explored the stochastic behavior of an interesting mutant that provides a significant quantitative test of our current understanding of the cell cycle regulatory network as embodied in a detailed mathematical model. A stochastic version of this model captures the experimental observations reasonably well. Remaining discrepancies between the experimental and simulated data suggest areas where the model needs to be improved in the future.

While this paper has concentrated on the cell cycle in budding yeast, it is motivated by the overarching goal of understanding how to use stochastic phenotypes to improve our understanding of biological systems as embodied in mathematical models. It is expected that such stochastic phenotypes will prove important in medicine for understanding diseased states and therapeutic interventions.

Materials and Methods

Strains and media.

From F.R. Cross (Rockefeller University), we obtained Saccharomyces cerevisiae strain RW54a (MATa clb5::HIS3 CLB2-db trp1::TRP1::GAL-SIC1 leu2 ura3 his3 ade2 can1), which lacks the CLB5 gene, carries a CLB2 gene that lacks the normal destruction box and is kept alive by expressing Sic1 from a galactose-inducible promoter. Yeast strain w303 (MATa leu2-3,112 trp1-1 can1-100 ura3-1 ade2-1 his3-11,15), which is the background of RW54a, was used as a control. Cultures were grown overnight in Synthetic Complete (SC) medium (6.7 g/L yeast nitrogen base, 1.92 g/L Yeast Synthetic Drop-out without tryptophan, 4 mg/L tryptophan) containing 20 g/L galactose. For observation on the microscope, cultures were washed twice in phosphate-buffered saline (PBS) and resuspended in SC medium containing either 20 g/L raffinose or 20 g/L glucose.

Microscopy.

To allow the simultaneous observation of both wild-type and mutant cultures, a standard #1.5 coverslip was divided into two halves with RTV silicone and allowed to cure for 24 hours. 3.5 µL of either the wild-type or mutant culture was added to each half of the coverslip, and each was covered with a thin slab of SC agar containing the appropriate carbon source. A microscope slide was then placed on top of the agar slabs, and sealed to the coverslip with paraffin to reduce sample evaporation and cell motion.

Twenty representative fields-of-view were manually selected for each culture on the slide, and phase contrast images were acquired at 4 minute intervals over a 10 hour period on a DeltaVision Core microscope (Applied Precision, Inc.,) with a 60x PlanApo PH3 phase-contrast, oil immersion objective (NA = 1.4). This system has a motorized x-y-z stage, automatic focusing, motorized illumination shutters and a CoolSNAP HQ2 CCD camera (Photometrics).

Image processing.

Budding events were manually recorded for each cell by identifying the frame in which a bud protrusion was first visible. This information was then used to calculate the interval between consecutive budding events for an individual cell (inter-bud time of a mother cell) and the interval between the emergence of a bud and the first budding event for the resulting cell (birth to bud time of a daughter cell).

Conversion of deterministic model to a stochastic model.

The mathematical cell cycle model used in this work is based on reference 14. This deterministic model is written in terms of dimensionless concentrations and uses phenomenological rate laws, such as Michaelis-Menten. To simulate this model stochastically, we converted the model from dimensionless variables, [S_i]_{dimensionless}, to numbers of molecules per cell by defining a set of characteristic concentrations C_i for each species such that the concentration of each species is [S_i] = C_i [S_i]_{dimensionless} and the number of molecules per cell is N_i = [S_i]·V·N_A, where V is cell volume (30 fL) and N_A is Avogadro's number. These characteristic concentrations are listed in Table 3 and the details of the conversion are contained in reference 52. The phenomenological rate laws in the model were treated as reaction propensities and the temporal evolution of the model was computed using Gillespie's stochastic simulation algorithm.16

Some parameters of the Chen-2004 model were changed slightly to increase the importance of Clb5 in wild-type cells, allowing stochastic simulations of the mutant strain to conform more closely to the experimental results. These minor changes (detailed in Table 2) did not change the deterministic results for the majority of mutants considered in the 2004 paper.

Stochastic simulations.

To provide reasonable initial conditions for the simulations, we attempted to mimic the experimental protocol. Starting with one wild-type cell in galactose medium (MDT = 159 minutes), we ran a pre-simulation for 2,000 min and saved to a file the biochemical state for each of the 4,615 cells that were present at the end of this simulation. To simulate the wild-type cells in raffinose, 1,000 simulations of 600 min duration were run, each starting with a single cell that was chosen randomly from the file of saved cells.

To simulate the CLB2-dbΔ clb5Δ GAL-SIC1 mutant strain, we started with one mutant cell in galactose medium with high Sic1 (synthesis rate increased to 6.66 times the basal rate) and ran the pre-simulation for 2,000 min, by which time the cell population was expanding exponentially. The biochemical state of each of the 1,290 cells present at this time was saved to a file. This pre-simulation mimicked the experimental procedure wherein the CLB2-dbΔ clb5Δ GAL-SIC1 strain was grown to log phase in galactose before the cells were transferred to either glucose or raffinose medium, repressing GAL-SIC1 transcription. To simulate the CLB2-dbΔ clb5Δ GAL-SIC1 mutants in glucose and raffinose, 1,000 simulations of 600 min duration were run, each starting with a single cell that was chosen randomly from the saved file.

In the deterministic model, events are used to mark cell cycle checkpoints and division. A typical deterministic event has the form:

if {[X(previous time step) > Threshold] AND [X(present time step) < Threshold]}

then (event actions are triggered),

by which we mean that when the value of variable X passes a specified threshold with a negative slope then the actions associated with the event occur. For example, cell division may be triggered when the decreasing abundance of Clb2 passes a specified threshold and causes the molecular contents of the cell to be divided between mother and daughter.

In a stochastic simulation, random fluctuations can cause a variable's value to cross a threshold many times in a short period of time, triggering a number of unwanted events. To prevent unwanted triggering due to noise, we introduce a second threshold to license the occurrence of an event. For example, the event condition above is replaced by

if {[X(previous time step) < LicenseThreshold] AND [X(present time step) > LicenseThreshold]}

then (EventFlag ← TRUE)

if {[X(previous time step) > EventThreshold] AND [X(present time step) < EventThreshold] AND EventFlag = TRUE}

then (event actions are triggered; EventFlag ← FALSE)

In this case, LicenseThreshold = 1.5 * EventThreshold. For an event triggered by X rising above a threshold, we set LicenseThreshold = 0.5 * EventThreshold.

Data processing.

The number doubling time, NDT, was computed by plotting the logarithm of the cumulative number of buds (divisions) as a function of time to produce a growth curve for the cells. Data for the time window 300 to 600 minutes was fit to a straight line using least squares and the NDT was computed as log(2) divided by the slope of this line.

To estimate the probability that the experimental inter-bud time was greater than a specified time T we used the Kaplan-Meier estimator.53 This estimator is frequently used in survival analysis to provide the maximum likelihood estimate of the survival function, which is equivalent to the probability distribution we are trying to estimate. The advantage of this estimator is that it allows us to account accurately for right-censored data—data for which we don't know the exact time interval but for which we do know that the time interval is greater than some value. Such censored data arises in our experiments because the inter-bud times associated with the first bud time of a cell, with the last bud time of a cell, and with cells that do not bud at all during the observation window, are not known exactly but are only known to be greater than certain values. We include all of this censored data in our estimation of the probability distribution, which is computed using the MATLAB command ‘ecdf’. The rightmost point plotted in these curves corresponds to the largest inter-bud time for which we observed consecutive budding events within the experimental window. Similar statements hold for the simulated data where we recorded division times as opposed to inter-bud times.

Author's Contributions

W.T.B., J.J.T. and K.C.C. conceived the study; D.A.B. and J.P. carried out the experiments; P.W., K.C.C. and W.T.B. developed the stochastic model; P.W., T.H.A. and Y.C. carried out the simulations; T.H.A., D.A.B. and W.T.B. analyzed the data; J.J.T. and W.T.B. wrote the initial draft of the paper and all authors edited the final version.

Abbreviations

db	=	destruction box
MDT	=	mass doubling time
NDT	=	number doubling time
APC	=	anaphase promoting complex
ODE	=	ordinary differential equation

Figures and Tables

Figure 1 Wiring diagram of the interactions involving Clb2 and Clb5 at the exit from mitosis. Solid lines indicate reactions, solid lines with filled balls at the ends indicate reversible association reactions and dashed lines indicate the influences of transcription factors or enzymes. A : indicates a complex. We assume that Clb2 and Clb5 are always complexed with Cdc28 and do not denote this explicitly. D denotes degradation by targeting the destruction box and KEN denotes degradation by targeting the KEN box.

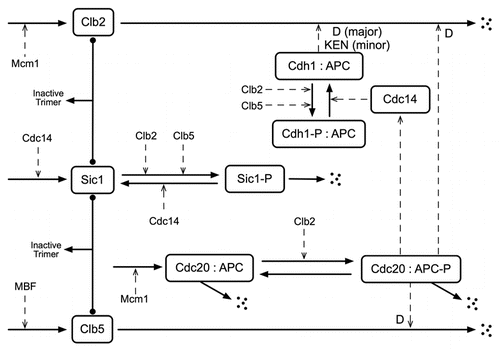
Figure 2 Depiction of time intervals defining inter-division and inter-bud times. The cell cycle time from division to division of the daughter, T_D and mother, T_M, are related to the division to bud times of the daughter and mother, T_dDb and T_dMb respectively and to the bud to division times, T_bDd and T_bMd respectively. This allows us to conclude that the bud to bud times for the daughter and mother, T_bDb and T_bMb respectively, should have approximately the same statistics as the corresponding division to division times.

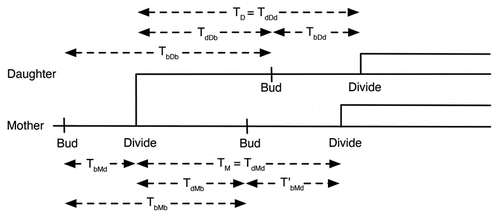
Figure 3 Comparison of wild-type and mutant cell growth in raffinose in experiments and simulations. (A) For each of three separate experiments (1 = blue, 2 = green, 3 = red) and simulation (black) the initial number of cells is plotted at t =-and at each bud event (division event for simulations) thereafter the number of cells is increased by one for wild-type (+) and mutant strains (•). The lines are least-squares fits to the points for t > 300 min (solid: wild-type, dashed: mutant). (B) Probability that the time between buds is greater than a specified time for the three experiments and a simulation depicted in (A). Line colors and styles correspond to the same datasets shown in (A).

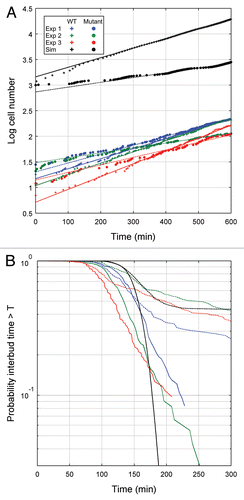
Figure 4 Histograms of cell cycle duration in mother and daughter cells. Budding events were tabulated manually and the time between the emergence of consecutive buds was calculated for wild-type cells (A–C) and for mutant cells (E–G) in experiments 1–3, respectively. For simulated data (D and H), the time between division events, rather than budding events, was used for wild-type cells (D) and for mutant cells (H).

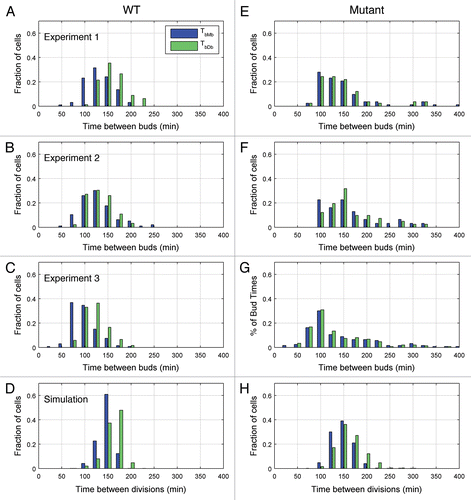
Figure 5 Dendrographs for typical cells. Example lineages of three wild-type cells (A) and three mutant cells (B), demonstrating the various proliferation patterns observed. Dendrographs from simulated wild-type and mutant cells are shown in (C and D), respectively, for comparison. In the figure, branch points occur at new budding events, for the experimental data, and at division events for simulations. Cell ID is an arbitrary identifier used for cell tracking.

Table 1 Statistical properties for cells growing on raffinose

	Experiment			Simulation (f = 0.48)
Exp. No./Simulation parameters	1	2	3	MDT = 160 V = 30 fL	MDT = 160 V = 15 fL	MDT = 150 V = 30 fL
Wild type
TbMb/TdMda	132 (30)	129 (38)	98 (28)	149 (12)	147 (16)	139 (13)
TbDb/TdDda	160 (26)	132 (27)	122 (26)	166 (14)	164 (17)	155 (14)
N(tend)	210	210	270	26715	19292	22469
NDT	155	138	120	159	161	149
CLB2-dbΔ clb5Δ
TbMb/TdMda	151 (65)	165 (63)	144 (80)	148 (24)	148 (30)	142 (23)
TbDb/TdDda	151 (63)	164 (53)	143 (82)	162 (29)	163 (34)	152 (27)
N(tend)	217	113	296	2811	3431	2605
NDT	173	314	205	322	284	347

Mean (standard deviation).

a For experiments, the value is the time in minutes from one budding event to the next for mothers (T_bMb) and daughters (T_bDb), while for simulations the value is the time in minutes from one division to the next for mothers (T_dMd), and daughters (T_dDd). Note: T_bDb represents the cycle time of the daughter from when it first appears as a bud in the mother to when the daughter produces its first bud.

Table 2 Changes to the parameters of the Chen-2004 model to increase the importance of Clb5

ksb5′ = 0.001 (0.0008)	kdb5″ = 0.08 (0.16)	ec1b5 = 0.4 (0.1)
ef6b5 = 0.2 (0.1)	kppc1 = 3.8 (4)	kppf6 = 3.8 (4)
eicdhb5 = 16 (8)	eorib5 = 0.3 (0.9)	ebudb5 = 0.25 (1)
ka20′ = 0.06 (0.05)	ka20″ = 0.18 (0.2)	kdb2p = 0.12 (0.15)
ec1b2 = 0.4 (0.45)	ef6b2 = 0.52 (0.55)	eicdhb2 = 1.4 (1.2)

Numbers in parentheses represent the original parameter values.

Table 3 Characteristic concentrations of the species used in the mathematical model

Species	Characteristic concentration (nM)	Species	Characteristic concentration (nM)
Cln2	40	Swi5	57.5
Clb2	40	BUDa	10
Clb5	40	Bub2b	100
Sic1	40	C2, F2	40
Cdc6	40	C5, F5	40
Cdc20	150	CKIT	40
Cdh1b	100	Cln3	40
Cdc14	18	IEb	100
Net1	18	Mad2	40
Esp1	3.3	ORIa	10
Pds1	3.3	SPNa	10
Cdc15	8	PE	3.3
Lte1	10	PPXb	100
SBF	110	RENT	18
Mcm1	100	Tem1	20

a BUD, ORI and SPN are timing variables and we used a concentration of 10 nM to introduce reasonable noise into these timings.

b For IE, Cdh1, Bub2 and PPX, the characteristic concentrations are unknown and so we assumed 100 nM as a reasonable guess. All other concentrations were approximated from data given in references 19 and 54.

Acknowledgements

We thank Fred Cross (Rockefeller University) for generously providing us with the CLB2-dbΔ clb5Δ GAL-SIC1 mutant strain and with advice about culturing yeast cells and making single-cell measurements. This work was supported by grant R01-GM078989 from the National Institutes of Health.