Characterizing how and when a way of proving develops in a primary mathematics classroom: a commognitive approach

Abstract

In this study we aim to characterize a way of proving which can be produced in a primary mathematics classroom and explore the factors that influence these processes and lead to changes in the way of proving. Assuming proving as a socially embedded activity, we conceptualize it as the interplay between ‘construction’ and ‘substantiation’ based on a well-established theoretical framework in mathematics education: the commognitive framework. A tangible proving task was designed, based on the idea of operative proofs, and implemented in a fifth-grade classroom in England. We analysed the construction and substantiation which fairly associated with discursive features (word use, visual mediator, narrative, and routine) during the proving process. The results show that the interplay between construction and substantiation developed progressively rather than in a straightforward manner, in which previously constructed narratives are reconstructed or substantiated in a more general context. This finding is relevant to understand the factors that might influence primary students to change the use of examples and the way of proving when used as a communicational means in proving. Our study has implications for possible continuity to proving activities in secondary schools, and thus contributes to advancing the research on proving in primary schools.

KEYWORDS:

• Commognitive framework
• operative proofs
• primary schools
• proving

1. Introduction

Proving is an essential but challenging activity in mathematical learning. Recent curricula in various countries require proof and proving to be taught at all levels (e.g. in the Common Core State Standards for School Mathematics in the United States (CCSSI;, 2010) and in the National Curriculum for Mathematics from the Department for Education (DfE; 2013) in England). Although research on proof and proving has been rapidly expanding in recent decades, mathematics education researchers acknowledge that what constitutes ‘proof’ and ‘proving’ is debatable (e.g. Mariotti et al., 2018; Reid & Knipping, 2010; Stylianides et al., 2016; Stylianides et al., 2017). This implies that the meaning of proof and proving may vary according to the researcher’s perspective or epistemology (Balacheff, 2008). For instance, Stylianides et al. (2017) state that there are three different research perspectives, which refer to different conceptualisations of proving:¹

• Proving as problem-solving: These studies aim to understand the skills, competencies, and dispositions that students need to produce an adequate performance in proof-related activities (e.g. Komatsu, 2016; Kosko, 2016; Reid & Zack, 2009; Selden & Selden, 2013; Stylianides & Al-Murani, 2010; Weber & Alcock, 2004).

• Proving as convincing: These studies aim to understand students’ or teachers’ standards of mathematical conviction and their proximity to acceptable standards in the discipline (e.g. Balacheff, 1988; Bell, 1976; Bieda & Lepak, 2014; Flores, 2006; Harel & Sowder, 1998).

• Proving as a socially embedded activity: These studies investigate how proof is practiced within mathematical and classroom communities (e.g. Fukawa-Connelly, 2012; Hemmi, 2008; Herbst & Chazan, 2003; Mueller et al., 2012; Whitenack & Knipping, 2002).

Per Stylianides et al. (2017), the first two perspectives implicitly (or explicitly) view proving as an individual activity for problem-solving or convincing, but the third perspective treats proving within a broader mathematical activity, which usually occurs in a social context to develop an acceptable proof in a given community. Although the first two perspectives have been well developed and many theoretical constructs are commonly used within each, the third perspective is less developed and does not yet have common theoretical constructs (Stylianides et al., 2017).

Here, we address the research perspective of proving as a socially embedded activity to contribute to further developing theoretical grounding within this perspective by taking a discursive (commognitive) approach to proof and proving. Sfard’s (2008, 2012, 2020) commognitive framework conceives mathematical learning as a communicative activity and an initiation into the mathematical community’s discursive practice. Despite many commognitive studies, the area of proof and proving using commognitive theory as a research topic remains relatively unexplored. While the commognitive framework is not a domain-specific theory of proof and proving, it provides a set of notions suitable for conceptualizing proof and proving as a discursive activity and characterizing its process in a theoretically coherent way.

Another issue addressed here is regarding proof and proving in primary schools. Researchers report how primary school students can engage in proof and proving (e.g. Ball et al., 2002; Komatsu, 2010; Maher & Martino, 1996; Reid, 2002; Reid & Zack, 2009; Stylianides, 2007, 2016). These studies suggest, for instance, the importance of proving tasks which enable primary students to engage in proving, and the importance of different informal representations which have the potential to develop more formal proving in upper grades. However, further investigation in this research area is needed for both theoretical and empirical aspects.

First, Stylianides and Stylianides (2017) concluded that further research into the design of classroom-based interventions regarding proof and proving in primary schools is needed because of ‘the gap that exists currently in many countries between elementary and secondary school mathematics with students’ abrupt introduction to proof in the secondary school’ (p. 124). Our study contributes to literature by addressing the classroom-based research regarding proving in primary schools by focusing on the transition to proof and proving in secondary schools. In relation to this point, Campbell et al.’s (2019) synthesis implied that this gap also exists in the publications of research studies as few articles related to proof in primary grades were identified in their literature survey, though they note that ‘it is possible that the word search used for this review left out articles related to proof and argumentation in the primary grades’ (Campbell et al., 2019, p. 768). In fact, the proof-related terms used in the research article for the primary grades may be diverse (e.g. Widjaja et al., 2020). To bridge this gap regarding the research terminologies, we introduce some theoretical terminologies regarding proof and proving based on the commognitive framework.

Second, Campbell et al. (2020) argued that most existing research studies targeting the early primary grades used proving tasks that did not require a general argument, but the students used argument ‘to communicate with their classmates and explain their thinking across specific cases’ (p. 766). Although it is reasonable that younger students can only engage in proving with specific examples, our study creates an opportunity for primary students to explore a general argument in their proving activities.

Third, regarding students’ proving activities across grades, the diverse formulations of process and outcomes of proving in primary schools must also be considered. Reid and Knipping (2010) highlighted that previous studies discussed different types of proofs; examples include Harel and Sowder’s (1998) conceptualization of external, empirical, and analytical proof schemes. Although such classifications can be useful to describe and distinguish students’ understanding of proofs in different grades, researchers are still working towards a coherent theoretical approach to how and when a type of proof can develop into another type (e.g. Ahmadpour et al., 2019). As earlier studies reported, a certain type of proof can be produced even by primary school students. However, it is challenging to detect such development due to the complex or auxiliary activity of proving, especially in primary mathematics classrooms. Our study attempts to contribute to this aspect by conceptualizing different types of proofs and investigating the dynamic process in the transition between them.

Accordingly, in this study we aim to characterize a way of proving which can be produced in a primary mathematics classroom and explore the factors that influence these processes and lead to changes in the way of proving. To achieve this, we first develop our theoretical approach to proving based on the commognitive framework and design a proving task that can help primary students engage in proving activities; we then analyse their classroom activities from the commognitive standpoint. By doing so, the commognitive approach can contribute to advancing the research perspective of proving as a socially embedded activity as well as developing methodology to characterize students’ way of proving and their development in a theoretically coherent way.

2. Theoretical foundation

In this section, we first describe the commognitive framework’s general tenets and then link it to the analysis of proof and proving by incorporating different types of proofs.

2.1. Commognitive framework

In Sfard’s (2008) commognitive framework, ‘commognition’ combines ‘communication’ and ‘cognition’ because ‘these two processes are different (intrapersonal and interpersonal) manifestations of the same phenomenon’ (Sfard, 2008, p. 296). This framework adopts two epistemological assumptions: a participationist view of learning and non-dualist view of knowledge. The former states that ‘mathematics learning is tantamount to becoming a member of a mathematical community’ (Sfard, 2012, p. 2), and the latter means that knowledge is not expressed in discourse but is itself a form of discourse.

In most commognitive research, four features of mathematical discourse are used to analyse mathematics learning: word use (mathematical vocabulary and ordinary words with special mathematical meanings); visual mediators (physical, diagrammatic, or symbolic mediators of mathematical objects); narratives (e.g. theorems, definitions, and computational rules endorsed or rejected in mathematical communities); and routines (regularly employed repetitive activities and sets of meta-rules). A meta-rule (meta-discursive rule) in routines is ‘an all-encompassing category that partially overlaps with the three former characteristics [of word use, visual mediators, and narratives]’ (Sfard, 2007, p. 576). Accordingly, the development of mathematical discourse can be conceived at the object level or the meta-level (Sfard, 2020):

• Object-level developments result in extending the existing sets of endorsed narratives about already constructed mathematical objects.

• Meta-level developments involve changes in the meta-rules of the discourse.

A meta-discursive shift may occur when new object-level discourse is governed by different meta-rules from those previously learned (Sfard, 2008).

2.2. Proof and proving in the commognitive framework

According to Sfard (2008), ‘exploration is a routine, whose performance counts as completed when an endorsable narrative is produced or substantiated’ (p. 224). Thus, ‘proving’ is an example of mathematical explorations in the commognitive framework. There are three types of exploratory routines:

[C]onstruction, which is a discursive process resulting in new endorsable narratives; substantiation, the action that helps mathematists decide whether to endorse previously constructed narratives; and recall, the process one performs to be able to summon a narrative that was endorsed in the past. (Sfard, 2008, p. 225; original emphasis)

Here, we focus on construction and substantiation, defining ‘proving’ as the process of communication with oneself or others that allows for the construction and substantiation of a narrative. This is adapted from Jeannotte and Kieran’s (2017) commognitive-framework-based definition of mathematical reasoning, although they do not explicitly mention construction and substantiation.² Our definition has several connotations. The notion of ‘proof’ is conceived in relation to the substantiation of a narrative:

To substantiate, one produces a proof – a sequence of endorsed narratives, each of which is deductively inferred from previous ones and the last of which is the narrative that is being endorsed. [emphasis added] (Sfard, 2008, p. 232).

This account can be considered formal proof (e.g. Blum & Kirsch, 1991), but other proof types can also be produced to substantiate a narrative to argue whether statements are true or false in a community. Thus, proving can be considered a process of producing a proof, but proving is not only related to the substantiation process—it is also related to construction because ‘in some cases, the process of construction, if correctly performed, is already the act of substantiation’ (Sfard, 2008, p. 232). Additionally, ‘the activity of substantiation is recursive: It may always expand, because the substantiation itself is a narrative that may become an object of substantiation’ (Sfard, 2008, p. 232). Furthermore, at object-level development, both constructing (i.e. a discursive process resulting in a narrative) and substantiating (i.e. a discursive process ensuring that a given narrative can be endorsed) are important proving routines. In contrast, at meta-level development, when and how a routine can change into another routine are essential. Thus, for the commognitive analysis of proving, the study can focus on the transition between construction and substantiation to characterize both object-level and meta-level proving.

2.3. Connection to other conceptualisations

The abovementioned definition of proving does not make it incompatible with other theoretical approaches. Stylianides (2007, 2016) defined proving as ‘broadly to denote the mathematical activity associated with the search for a proof’ (Stylianides, 2016, p. 11) and then provided a conceptualization of proof as a mathematical argument in a classroom community, composed of a set of accepted statements, modes of argumentation, and modes of argument representation. Stylianides’s notion of proofs is seemingly well-defined, but it acknowledges proving as a broader mathematical activity. For Stylianides (2016), a so-called ‘empirical argument’ (e.g. Balacheff, 1988) is excluded from proofs due to the invalid argumentation modes, although he viewed them as playing important roles. In contrast, our key notion is ‘proving’, which is theoretically framed but acknowledges different types of proofs, including empirical arguments (as we will mention later). Another of our conceptualization’s characteristics is viewing proving as communicating, which can be linked to the communicative function of proof (De Villiers, 1990; Hanna & Jahnke, 1996) as well as change the epistemic value of a narrative (Duval, 2007). Regarding the changing of the epistemic value, Harel and Sowder (1998) defined ‘proving’ as the process employed by an individual to remove or create doubts about the truth of an observation. In contrast, from a commognitive standpoint on proving, the epistemic value of determining a statement true or false depends on the shared discourse (meta-rules and endorsed narratives) in a given community (Jeannotte & Kieran, 2017).³ Additionally, the interplay between construction and substantiation has much in common with what Stylianides (2008) called ‘reasoning-and-proving’, although its conceptualization does not consider the role of social context (or communication) as central. Thus, our definition relates to earlier studies in this area, and what distinguishes our approach from related studies or constructs is that it allows proof and proving to be characterized using a set of theoretical notions (e.g. the four discursive features and two levels of proving). Hence, both individual and social processes of proving can be described in one theoretical framework.

2.4. A way to characterize proof and proving: an analytical framework

The analytical framework we use refers to a specialized version of the four features of mathematical discourse, adapted for proof and proving in primary schools. The examples are from a simple proving task, ‘What happens when you add any two odd numbers’.⁴

• Word use: verbal and written keywords in the proving process (e.g. odd numbers, even numbers, singletons)

• Visual mediators: physical, diagrammatic, and symbolic mediators according to different proof types (e.g. concrete objects such as counters, generic examples)

• Narratives: statements subject to endorsement or rejection (e.g. the sum of any two odd numbers is always even)

• Routines: construction and/or substantiation (e.g. activities of producing and explaining the narrative)

Visual mediators for proving refer to different types of ‘proofs’. To clarify this, we refer to pre-formalist categorisations of proofs (e.g. Blum & Kirsch, 1991; Brunner & Reusser, 2019; Semadeni, 1984; Wittmann, 1996, 2009, 2019; Wittmann & Müller, 1990) which allow us to legitimate proofs at different levels and are useful for designing a suitable proving task. Per Reid and Knipping (2010), ‘[f]or the preformalists the nature of the premises (concrete objects, etc.) are of central importance’ [emphasis added] (p. 130). This perspective enriches the analysis of visual mediators in the proving process.

We summarize the types of proofs as three categories (the descriptions below are adapted from Brunner and Reusser (2019) and Reid and Knipping (2010)). A ‘formal-deductive proof’ can be translated into a commognitive account of proof, as cited from Sfard (2008).

• Experimental approaches (proofs)⁵: verification is based on concrete examples or physical objects; the conclusion is restricted to such particular cases.

• Operative proofs: requires action, manipulation, or concrete demonstration but is not tied to the concrete examples, yielding generally valid conclusions; this type uses little symbolism but is formalisable in principle.

• Formal-deductive proofs: a deductive process of making statements occurs within the rigid bounds of a set of well-defined rules and formal language; the stepwise deduction of a statement from other statements makes logically valid conclusions.

In this study, we focus on experimental approaches and operative proofs, for which physical and diagrammatic mediators are often used, but there is a significant difference regarding the epistemic status of their ‘examples’. Operative proofs employ so-called ‘generic examples’ (Balacheff, 1987, 1988; Healy & Hoyles, 2000; Mason & Pimm, 1984) in which a particular case stands for all possible cases; experimental approaches lack this characteristic (see also Brunner & Reusser, 2019). For example, in an operative proof such as ‘Any odd number has a singleton. When two odd numbers are combined, no singleton is preserved because the two singletons form a pair, so the result is always even’, concrete objects (e.g. counters) can be used as generic examples (Figure 1). In our analysis, we distinguished a generic example from a particular example, considering whether it is used as a representative case of the narrative without relying on properties only applicable to the particular examples. Henceforth, in this paper, we use ‘evolution (or evolve)’ to refer to the transition from the experimental approaches to the operative proofs.

Figure 1. A generic example.

Based on these theoretical standpoints, our research hypothesis in this paper is as follows. A way of proving as a socially embedded activity can be characterized by two strands: proof types (experimental or operative) and proving routines (construction or substantiation). Accordingly, the evolution of proving can be identified as meta-discursive shifts, that is, when and how a proof type or proving routine can change into another. In this shift, the communicative role of proving, linked to changing the epistemic value of a narrative, is crucial.

Additionally, to analyse discursive processes and meta-rules, we observe students’ gestures. Per Sfard (2009), ‘gesture is a body movement fulfilling communicational function’ (p. 194), and ‘gestures are invaluable means for ensuring that all the interlocutors “speaks about the same mathematical object”’ (p. 197). Gestures can indicate a communicative role of proving. Concerning the operations (represented by ‘arrows’) in Figure 1, combining two odd numbers is crucial to the effectiveness of operative proofs. In the classroom, both utterances and gestures are important indicators of a communicative role in the proving process.

2.5. Research questions

Based on the above theoretical orientations, our analysis is guided by the following research questions:

1. How do construction and substantiation routines affect word use, visual mediators, and narratives produced by primary school students in the proving process?

2. How are different types of proofs (experimental and operative) produced through the interplay between construction and substantiation routines?

Both questions relate to the transition between experimental approaches and operative proofs which primary students might utilize, but they concern different levels in terms of discursive development. Question 1 considers proving at the object-level development (object-level proving), and Question 2 considers it at the meta-level development (meta-level proving). We show how our analytical framework can characterize students’ proving process and the production of different types of proofs. Below, we describe a task design to engage primary school students in proving.

3. Methodological considerations

3.1. Study context and task design

The study context is a teaching experiment within a classroom lesson, and its design was oriented for investigating proving activities in primary schools. We considered explorative proving activities at the lower secondary level (Miyazaki & Fujita, 2015), in which students produce statements, plan and construct proofs, and review them to improve learning. Considering operative proofs, our study adapts such explorative activities for primary students to make proving activities possible for them, allowing them to visualize abstract mathematical structures or relations using suitable tangible materials and pictures. Accordingly, our methodological approach is regarded as topic-specific design research (Gravemeijer & Prediger, 2019) for the case of proving in a primary classroom.

We considered the following properties of operative proofs (Wittmann, 2009, p. 254) as design principles (cf. Kieran, 2019):

1. they arise from exploring a mathematical problem;

2. they are based on operations with ‘quasi-real’ mathematical objects;⁶

3. they are communicable in a problem-oriented language with little symbolism.

Based on the first principle, three proving tasks were developed for a series of lessons, such as ‘always 198’, ‘ANNA numbers (differences between 2112−1221, 3113−1331, etc.)’, and ‘sums of consecutive numbers’. In this study, we focused on the first task, ‘always 198’, designed to be implemented in the first lesson, introducing students to operative proofs. Before implementing this lesson, students did not receive explicit instructions about how to solve the task, nor was it accompanied by any formulated statement, with the expectation that they will explore and develop different patterns, produce statements, refine them, and then provide (operative) proofs. We considered the first lesson as suitable and sufficient case to illustrate the proving activities in our study because students’ first encounters with a new way of proving involved the descriptions of complex yet fruitful characteristic aspects, compared with the subsequent lessons.

Table

Choose a three-digit number for which the hundreds, tens, and ones are consecutive numbers. As you can see below, you can choose ‘123’, for example.  1 2 3 4 5 6 7 8 9Add 198 to the three-digit number you chose. What do you notice? Can you explain it?

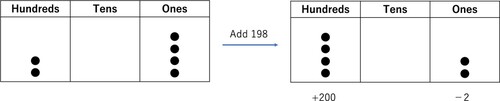
This proving task is based on a general number pattern: ABC and CBA numbers are pairs of three-digit integers, such as (123, 321), (124, 421), etc., and their difference is always ‘99 (C−A); C > A’. It is a specific version of an ‘if-then’ formulation: if you add 198 to the three-digit integers for which the hundreds, tens, and ones are consecutive numbers, the sum becomes the number for which the digits are reversed from the original integers’ digits. Here, ‘a proving task’ does not mean that it produces a single narrative, but it may lead to different narratives in the process and product of proving as explorative activities. Therefore, the above task was designed as an initial proving task in the lesson.

Concerning the second principle, our task design represented abstract mathematical relations with physical mediators (i.e. manipulatives such as place-value tables and counters; Figure 2) to enable primary school students to explore operative proofs.

Figure 2. Operations with place-value table and counters.

Concerning the third principle, our task was designed to be communicable with ordinary words, for example, ‘taking counters’, ‘adding counters’, and ‘reverse (swap over)’. Although some mathematical words (e.g. ‘three-digit number’, ‘addition’, and ‘multiples’) are inevitable, the task does not require algebraic symbols or formulas. Thus, our task design covers all properties of operative proofs.

The data were collected in a small classroom with seven students (Grade 5; 9–10 year olds) in England in December 2014. The school agreed to implement lessons with the three designed tasks as enrichment activities with ethical permission from University of Exeter. The students were selected because the class teacher (CT) recognized them as possessing ‘relatively higher abilities in mathematics’. The CT chose the student group to fit the school’s busy timetable, in consultation with the second author. The second author led each lesson (45–60 min), introducing the problem, supporting the formulation of reasoning, and summarizing the findings, but the CT also provided support. Accordingly, the lessons can be considered as teaching (or design) experiment lessons rather than ordinary classroom teaching. However, the teaching was conducted in the mathematics classroom where the students usually work rather than in a laboratory setting. Although the lessons can also be considered an intervention, we aimed to investigate how well the approach worked for this age group rather than seeking to improve participants’ mathematical attainments. Each lesson was video-recorded, focusing on students’ activities.

3.2. Method of analysis

Our analytical method consisted of three phases. First, we divided the video data transcript into episodes, identified according to the narratives constructed or substantiated therein. The following four narratives (NA1–4) were reconstructed and labelled by the authors to clarify the episodes. Each episode consists of ‘line’, ‘time (min/sec)’, ‘what is said’, and ‘what is done’. We mainly analysed the transcribed episode, but the video data were important to understand students’ actions (manipulations) on concrete objects. Therefore, some snapshots from the video data have been included in this paper as references to supplement our interpretations.

• [NA1: Consecutive digit numbers] If you add 198 to the three-digit integers for which the hundreds, tens, and ones are consecutive numbers (e.g. 123, 234, 345 …), the sum becomes the number for which the digits are reversed from the original integers’ digits (321, 432, 543, etc.).

• [NA2: Difference between hundreds and ones is two] If you add 198 to the three-digit integers for which the difference of hundreds and ones is two (e.g. 143, 204, 436 …), the sum becomes the number for which the digits are reversed from the order of the original integers’ digits (341, 402, 634, etc.).

• [NA3: Differences between hundreds and ones are one, two, three … ] If you add 99, 198, 297 … to the three-digit integers for which the differences between hundreds and ones are one, two, three … , the sum becomes the number for which the digits are reversed from the original integers’ digits.

• [NA4: Multiples of 99] The difference between two three-digit integers for which the hundreds and ones digits are reversed makes multiples of 99.

Second, episodes were interpreted to identify whether the episode concerns construction or substantiation of the narrative, and then each episode was analysed to reveal four characteristic aspects of proving discourse (word use, visual mediators, narratives, and routines) and their relations. For example, we interpreted an episode as construction routine if the teacher or students shifted their foci from a narrative to another (new) narrative (e.g. NA1 to NA2). We also interpreted an episode as substantiation routine if the teacher or students provided a justification of the given narrative to endorse.

Finally, we analysed more deeply when and how different proof types are produced and evolve to characterize the meta-discursive shift. Students’ use of examples was key to this analysis because the experimental approach relies more on the particular examples, while the operative proof is not tied to the particular examples but focuses on the generic examples.

4. Findings

Table 1 lists episodes identified according to the four narratives and routines (construction or substantiation) in proving as a socially embedded activity. Each narrative was interactively constructed and substantiated (e.g. NA1 was substantiated after NA2 had been constructed). For a comprehensive analysis, we divided episodes into two phases. Phase I focuses on initial stages of students’ proving based on an experimental approach to substantiation, while phase II reveals the evolution from experimental to operative proofs through the interplay of narrative construction and substantiation. We then summarize our main results and provide additional analysis of the discursive development.

Table 1. A list of identified episodes, routines, and narratives.

Phase of analysis	Episodes	Routines	Narratives
Phase I	-	Construction	NA1: Consecutive digit numbers
	1	Substantiation
	2a	Construction	NA2: Difference between hundreds and ones is two
Phase II	2b	Substantiation
	3a	Construction	NA3: Differences between hundreds and ones are one, two, three …
	3b	Substantiation
	4	Construction	NA4: Multiples of 99

4.1. Phase I

4.1.1. Construction of NA1

First, we describe students’ activities in NA1 (we did not include an episode for its construction since it was involved in the problem implicitly and then became more explicit through exploration). Initially, students were not allowed to use physical manipulatives (place-value table and counters) but needed to perform calculations to find a pattern. This activity (adding 198 to the three-digit number) gradually developed into a routine performed to construct NA1, when students became aware that ‘123 + 198 = 321, 234 + 198 = 432, 345 + 198 = 543 … ’ and of the patterns students called ‘swap over’. The teacher then asked them to explore ‘why the hundreds and ones are reversed’. Students were encouraged to use physical manipulatives to find and explain the pattern (the place-value table’s format on their worksheet is similar to Figure 2).

4.1.2. Construction of NA2

Episode 2a shows how a student’s (S5) construction of NA2 relied on written calculation to find the sum of 204 and 198 (line 97), but another student (S7) used physical manipulatives to show the difference between 204 and 402 (line 101). The teacher gave the example ‘204 + 198 = 402’, hoping S7 might see that hundreds, tens, and ones do not have to be consecutive numbers and that the pattern can be generalized. At first, he did not see why the teacher gave the number 204 instead of 234. Nevertheless, after manipulating the counters, he clapped his hands and expressed his realization (line 101), which was linked to constructing NA2. For him, ‘204 + 198 = 402’ was a particular but crucial example for noticing that ‘the difference between two numbers [the ones and the hundreds] is two’, which is key to constructing NA2. However, the other students were not aware of what S7 had noticed, which was limited to his individual process.

Episode 2a.

Table

Line	Min	Sec	Speaker	What is said	What is done
96	11	2	T	Yes, how about that one?	The teacher wrote a number, ‘204’, on the students’ sheet.
97	11	3	S5	204?	S5 started calculating 204 + 198 in written form. (Figure 3)
98	11	5	T	Yes, if we add 198?
99	11	13	S5	One ninety-eight so has to be …	S5 got an answer, ‘402’, from the calculation.
100	11	31	T	Yes, why is that? Because?
101	11	32	S7	[After manipulating the counters] The difference between … oh [claps his hands] … the difference between the two numbers has to be two!	S7 moved the counters from the ones to the hundreds. (Figure 4)

4.1.3. Substantiation of NA1

Episode 1 describes discourse regarding 123 + 198 = 321, in which the physical manipulation ‘moving two counters from ones to hundreds’ represents the arithmetic operations ‘−2’ and ‘+200’. S7’s utterances ‘taking two’ (line 113) and ‘adding 200’ are associated with his physically mediated actions with counters, so his substantiation method is still restricted to an experimental approach. In this initial stage, the teacher guided most of the activities for the substantiation. Subsequently, the students and teacher confirmed that this pattern works for other cases as well: 103 + 198 = 301, etc. Then, their focus moved to substantiating NA2.

Figure 3. Snapshot in episode 2a (line 97).

Figure 4. Snapshots in episode 2a (line 101).

Episode 1.⁷

Table

Line	Min	Sec	Speaker	What is said
112	13	24	T	What is happening? If I take from here?
113	13	27	S7	Is it taking two?
114	13	29	T	Yes, taking two. Well done, taking two but also?
115	13	34	S7	Adding 200.
116	13	35	T	Adding 200. So, therefore, 200 minus 2 will be?
117	13	41	SS	Ah. 198.
118	13	42	T	198. That is why always we will add 198 and then these two numbers. Now, 198, is this a magic number then?

4.2. Phase II

4.2.1. Substantiation of NA2

Episode 2b shows the discursive process of substantiating NA2, in which some students (at least S5 and S6) grasped S7’s realization, and S5 was eventually willing to explain it together with S7, convincing other students. Their activities in this episode were a substantiation routine showing the emergence of generic examples in the social process, in which their discourse moved away from particular examples such as each pair of three-digit numbers. In addition, S7 (line 148) used the gesture (two fingers up) to communicate with others. It seems that this gesture also helped use generic examples for substantiating because, for him, the repeated signs ‘two’ by way of his fingers pointing up might refer to all possible cases of the narrative ‘the difference between the ones and the hundreds is two’. Although the operative proofs based on the generic examples were not explicitly produced to substantiate NA2, his discourse, which was developing in this context, was accepted as ‘theory’ (line 144–145) or ‘mechanism’ (line 152) within the classroom.

Episode 2b.

Table

Line	Min	Sec	Speaker	What is said	What is done
143	16	53	S7	You can just try any random number if you try to …
144	16	56	CT	What is your theory on that?
145	17	2	S7	Theory? I would say, the difference between the two numbers …
146	17	4	S5	Two numbers, the hundreds and the units, have to be two for it to work.
147	17	7	S7	But so, the difference between 6 and 8 [in 678] is two, the difference between 6 and 8 is two [in 698].	Pointed at several three-digit numbers (678, 698, etc.) to explain the difference between the hundreds and the ones.
148	17	10	S5, S7	The difference between 4 and 6 [in 456] is two, the difference between 1 and 3 [in 103] is two.	S5 and S7 kept explaining the pattern. S7 emphasized ‘two’ with his hand gesture (two fingers up). (Figure 5)
149	17	18	S6	Ah, right, I get it!	Reacted after listening to S5 and S7.
150	17	20	S5	The idea might be …
151	17	21	S4	Which one?
152	17	22	S6	So, there is going to be like a two-mechanism I will say.

4.2.2. Construction of NA3

In episode 3a, NA3 was constructed differently from NA1 and NA2. NA3 was first presented as a subsequent question by the teacher, ‘If you want to reverse the hundreds and the ones of a three-digit number, what number do you have to add?’, using ‘112’ as an example. Episode 3a (line 180) shows that physical objects shaped S7’s action to find a product, ‘99 (by simply calculating 100–1)’, and their explanation to another student (S5). In contrast, S5 still used written calculation (‘211−112’) to understand the answer, including when the teacher gave another example (‘318’, line 206). S7 was able to answer ‘495’ using the physical manipulatives (line 223). Here, these actions have been evolving into an operative proof, in which S7’s manipulations on counters ‘813−318’ act as generic examples because he no longer calculated ‘813−318’ to find the difference. Instead, he mentally worked out ‘500−5’. Although his approach was produced from his exploring to respond to the teacher’s question, it can be considered an aspect of the operative proof by referring to a series of patterns, ‘100−1, 200−2, or 500−5’. For him, ‘813−318 = 495’ was an example to represent the narrative ‘the difference between the ones and the hundreds is five’, which is another case of NA2. However, it has not yet evolved to the substantiation routine for NA3. We therefore consider that the students’ manipulations in this episode can be regarded as a trigger for evolving to the operative proof.

Figure 5. Snapshot in episode 2b (line 148).

Episode 3a.

Table

Line	Min	Sec	Speaker	What is said	What is done
180	23	45	S7	You are adding 99. Subtracted 1 from 100. If you want to swap the surrounds, the difference has to be [one].	Pointed at one counter on the ones and moved it to the hundreds. (Figure 6)
181	23	56	S5		Calculated 211−112 in written form. (Figure 7)
182	24	2	S7	That is 99.
206	25	40	T	How about 318?
207	25	44	S7	Oh, 318.
208	25	46	T	If I wanted to swap 813
223	26	23	S7	495	Moved five counters from the ones to the hundreds, then answered ‘495’ after mental calculation. (Figure 8)

4.2.3. Substantiation of NA3

In episode 3b, S7’s discursive process changes from experimental to operative proofs (similar to 3a but more explicitly) and undergoes further evolutions towards the substantiation of NA3. S7 makes a generic narrative (line 239), ‘the difference between the two numbers is what you take away’, interpreting ‘113’ and ‘318’ as generic examples. Furthermore, his utterance ‘the difference between two numbers … ’ was distinct from process-oriented operations like ‘adding’ or ‘subtracting’, focusing more on their products. Along with his generic narrative, his repeated actions (moving counters between the ones and the hundreds; see line 239) reveal gestures to communicate with others. In this episode, the operative proofs with generic examples explicitly mediate concrete objects but convey that substantiation can be generalized beyond particular cases.

Figure 6. Snapshots in episode 3a (line 180).

Figure 7. Snapshot in episode 3a (line 181).

Figure 8. Snapshots in episode 3a (line 223).

Episode 3b.

Table

Line	Min	Sec	Speaker	What is said	What is done
237	27	20	T	… You just calculated. Use that one to explain. Ask him what he is doing.	The teacher encouraged S5 to use the place-value table without the written calculation as S7 did.
238	27	29	S5	What are you doing?
239	27	30	S7	Well, I think … , the difference between the two numbers is what you take away. So, you know on 113, you have got the difference of two. So, you are moving the two from there and putting it on there. Or 318, you are taking away five from there and putting it on there because the difference between 3 and 8 is 5.	He moved five counters from the ones to the hundreds. (Figure 9)He repeatedly moved five counters from the hundreds to the ones. (Figure 10)
240	28	1	SS	Ah, right.
241	28	4	S7	And we get 813; that is how you do it.
242	28	10	S6	That is clever. That is good. Yes.

4.2.4. Construction of NA4

At the lesson’s end, the students and teacher reflected on their number pattern explorations and constructed a new narrative (NA4). Although NA4 was not substantiated, it can be validated because it was a generalized version of the already substantiated narratives (NA1, NA2, NA3).

Figure 9. Snapshots in episode 3b (line 239) [1].

Figure 10. Snapshots in episode 3b (line 239) [2].

Episode 4.

Table

Line	Min	Sec	Speaker	What is said
269	30	32	T	Now well done, really, really impressed by you all, actually. We have got 99, 198, 297, 396, 495 … yes it works. What are they? It is a silly question, but what is the relationship? Okay, let us …
270	31	18	SS	All the 90s
271	31	22	S7	It is multiples of 99!
272	31	23	SS	All multiples of 99!
273	31	24	S7	Multiples of 99!

4.3. Characterizing object-level and meta-level proving

4.3.1. Four discursive features

Based on this analysis, we summarize our main results below in terms of the four discursive aspects. These findings are regarded as characteristics of the object-level proving in the classroom.

• Word use. The utterance ‘swap over’ indicates that what students found in the number patterns and their different utterances to explain them evolved from being process-oriented (e.g. ‘taking two’ and ‘adding 200’ in episode 1) to being more product-oriented (e.g. ‘the difference between 4 and 6 (in 456) is two, the difference between 1 and 3 (in 103) is two’ in episode 2b). Eventually, this became a generic narrative such as ‘the difference between the two numbers is what you take away’ (episode 3b).

• Visual mediators. Physical manipulatives (place-value table and counters) were the main visual mediators, but the epistemic status of the physical objects developed over time. Initially, these objects were used for experimental approaches referring to particular examples (episode 2b), but later they were used for operative proofs to represent all possible cases (episode 3b).

• Narratives. Four narratives were identified and reconstructed, originating from the initial problem, with structural relations between them (i.e. NA3 is a generalized version of NA1 and NA2). Although NA1, NA2, and NA3 describe operations such as ‘if you add … ’, NA4 refers to the number pattern’s structure.

• Routines. Written (vertical) calculating (e.g. 123 + 198 = 321) was the initial routine in the classroom. Construction and substantiation developed recursively, and substantiation sometimes occurred after new narratives were constructed (as NA1 was substantiated after NA2 was constructed).

4.3.2. Meta-discursive development

Table 2 shows a summary of the evolution of proving in terms of the transition between two routines, which implies an aspect of meta-discursive development.⁸ To understand meta-level proving more deeply, we must reflect on when and how operative proofs with generic examples evolved from experimental approaches.

Table 2. A summary of the evolution of proving.

	Uses of examples	Types of proofs
Episode 1(substantiation of NA1)	Particular	Experimental
Episode 2a(construction of NA2)	Particular	Not identified
Episode 2b(substantiation of NA2)	Generic	Quasi-operative
Episode 3a(construction of NA3)	Particular and generic	Experimental and quasi-operative
Episode 3b(substantiation of NA3)	Generic	Operative

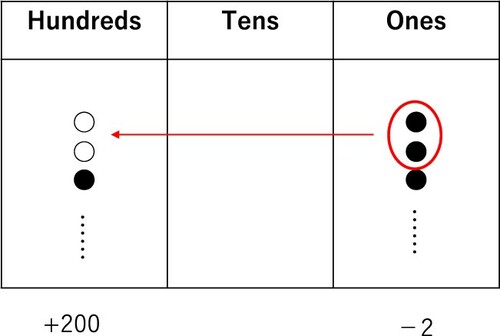
Generic examples were first observed in episode 2b (NA2 substantiation). The student’s (S7) action was developed from the previous episode (episode 2a, NA2 construction), in which S7 visualized a non-generic example, ‘204 + 198 = 402’, using counters, as in Figure 11. This action in Figure 11 has the potential to convey a pattern such as ‘+200 and −2 make 198’, which can be a structure beyond the particular case. It seems that S7 gained insight into this structure in episode 2a (line 101), possibly signifying an ‘Aha! moment’ in his mind, and he noticed that ‘the difference between the ones and the hundreds is two’ using ‘204 + 198 = 402’.

Figure 11. An experimental proof of NA2.

Although the pattern ‘+200 and –2 makes 198’ only regulated one student’s (S7) individual activity in episode 2a, this became more dialogic in episode 2b when he tried explaining his ‘theory’ to the other students. In this phase, the student started using several examples (e.g. 678, 698, or 456) as generic examples because these examples are considered representative cases to substantiate a generic narrative, ‘the difference between the ones and the hundreds is two’. This can be identified as resulting in changing (increasing) the epistemic value of NA2 among the group of students. Gestures also mediated substantiation in the dialogic process. In contrast, students’ use of generic examples with S7’s gestures in episode 2b were not yet connected to the operative proofs because the way of proving was not mediated by the manipulatives. Figure 12 shows a possible representation of the operative proof, which was not produced by students but based on our interpretation of episode 2b. What they called ‘two-mechanism’ (line 152) was something like this. Therefore, we call the type of proof observed in episode 2a a quasi-operative proof.

Figure 12. An operative proof of NA2.

The initial emergence of operative proofs was identified in episode 3a (NA3 construction), in which S5 was still working on the experimental approach (line 181), but S7’s activity (line 180, 223) was considered an implicit status of operative proofs (as we called it, a quasi-operative proof) when individually exploring the narrative. In this phase, the numbers (e.g. 211 and 112 or 318 and 813) acted as generic examples because the difference between two numbers can be found by the same actions (moving counters between the hundreds and the ones), conveying a common structure (e.g. ‘100−1, 200−2, 300−3, … ’). Subsequently, in episode 3b (NA3 substantiation), the operative proofs endorsed a generic narrative, ‘the difference between the two numbers (the hundreds and the ones) is what you take away’, which emerged to communicate with other students. This event is also critical for meta-discursive development because the substantiation was developed from the previously constructed narrative and resulted in changing the epistemic value of the narrative in the social context.

5. Discussion and conclusions

Here, we briefly describe our responses to the two research questions and discuss the study’s contributions, implications, and limitations.

5.1. Regarding the first research question

In Section 4.3.1, the findings regarding the first research question have already been described in light of four discursive factors that influence proving processes. Here, we summarize only the main points. In the classroom, an endorsed narrative was subsequently reconstructed as a more general endorsable narrative and then substantiated again in a more general context. Thus, such discursive processes developed through classroom interactions progressively rather than straightforwardly. Therefore, regarding proving routines, our findings support Sfard’s (2008) claim that ‘the activity of substantiation is recursive: It may always expand because the substantiation itself is a narrative that may become an object of substantiation’ (p. 232). Characteristic words and visual mediators produced by students were also affected by construction and substantiation routines. For example, the words used in students’ utterances changed from process-oriented to product-oriented, and the visual mediators often shaped students’ ways of proving. Although the teacher initially guided most of the students’ proving activities, the students played an increasingly important role in later stages. From a discursive perspective, this is important because it implies a process of becoming part of the classroom community.

5.2. Regarding the second research question

What distinguishes our approach from some recent studies examining proof and proving using the commognitive theory (e.g. Brown, 2018; Jeannotte & Kieran, 2017; Wang & Kinzel, 2014) is that we centralized the interplay between construction and substantiation to reveal the meta-level proving. This approach allowed us to characterize at least two main phenomena in our analysis. First, the classroom episodes illustrated that constructing a new narrative may lead to increasing the degree of generality in students’ discourse. This may then enhance the students’ use of generic examples as well as their evolution from experimental to operative proofs. Second, the episodes also demonstrated that substantiating the narrative is linked with increasing the epistemic value of the narrative in the classroom (see episodes 2b and 3b). This is related to the communicative role of proving. Referring to Table 2 (Section 4.3.2), our findings indicated that the operative proofs (and generic examples) were first produced implicitly in individual processes, but their ways of proving gradually develop to more explicit in the dialogic context. In our analysis, this shift is also linked to changing the epistemic value of the narrative. This implies conditions which allow students to change their approach from experimental to operative when using it as a communicational means. Thus, our study illustrated how students’ engagement with different types of proofs was developed through the interplay between constructions and substantiations. This may answer the second research question.

5.3. Contributions and implications

5.3.1. Contribution to the perspective of proving as a socially embedded activity

This paper offered the commognitive analysis of proving activities, defining proving as a process of communication with others or oneself that constructs and substantiates a narrative. Although our analysis is derived from one lesson, we could observe similar discursive characteristics in the subsequent lessons, that is, after the proving tasks were introduced by teachers, processes of evolutions of proving were characterized by interplays of narrative construction and substantiation, as we described in the first lesson. It is probably because that proving activities became much smoother as the students were familiar with the uses of counters and what they were expected to do (proving)⁹. This implies that the students’ activities with the teacher’s support in the first lesson were effective for initiating them into the operative proofs in the classroom community. Therefore, we believe that our approach can offer one way to theorize students’ proving activities coherently.

Some readers might consider that the commognitive terms (e.g. ‘construction’ and ‘substantiation’) could be translated into more familiar proof-related terms (e.g. such as ‘conjecturing’ or ‘verifying’), and they might then wonder about the benefit of this approach. However, one impact of defining the notion of proving without using such familiar terms is as follows. Our study adopted the perspective of proving as a socially embedded activity, conceptualizing ‘proving’ as a broader mathematical activity in a given community (Stylianides et al., 2017). To advance this perspective, we employed a broad but well-established theoretical framework for research in mathematics education rather than a domain-specific framework for research on proof and proving. In doing so, we utilized commognitive terminology to characterize proving activities and operationalize the theoretical constructs. This can also contribute to bridging the gap regarding research terminologies used to describe proof and proving in different grades (Campbell et al., 2019). On proving as a socially embedded activity, Stylianides et al. (2017) stated, ‘If explanation and communication are to be listed as goals of presenting proofs and an analytical tool to examine classroom behaviour, mathematics educators will need to operationalize these constructs’ (p. 249). We hope that we have addressed this issue as the commognitive analysis allowed us to identify and explain the characteristics of complex proving processes in a theoretically coherent way.

5.3.2. Contributions to research on proof and proving in primary schools

Here, we describe our paper’s three possible contributions to research on proof and proving in primary schools, in the form of response to what we mentioned as research limitations of previous works at the beginning of the paper. First, our study’s approach can contribute to the investigation of the challenges of ‘continuity’ across grades (Stylianides & Stylianides, 2017). In previous studies, the problem of the cognitive unity or rupture between conjecture and proof (argumentation and proof) has been debated for teaching mathematical proof in secondary schools (e.g. Mariotti, 2012; Pedemonte, 2007). Our findings show how primary students can appropriately experience conjecture and proof production and how these processes are interwoven, in which the interplay between the construction and substantiation of narratives is essential. For realizing this activity, we designed a task based on operative proofs (Wittmann, 2009) and investigated the task design through a classroom-based study, which has contributed to recent developments in this research area (Stylianides & Stylianides, 2017). Our findings demonstrated that this proof type is highly appropriate for primary school students and can be useful for advanced studies of mathematics in upper grades. In lower secondary schools, for example, the operative proof of NA3 can be translated into formal-deductive proofs as follows: (100a+10b+c)–(100c+10b+a) = 99(a–c); a > c. Operative proofs could help make sense of why the tens disappeared in the result. A similar task taught with algebraic symbols in lower secondary classrooms reportedly engaged students in proving the number pattern (e.g. Sasa et al., 2012; Tsujiyama et al., 2019), implying that our task design can be useful for different types of proofs in different grades.

Second, as Campbell et al. (2019) reviewed, most previous studies on early primary grades have paid scant attention to a general argument. We, therefore, designed a proving task which involved both specific and general arguments. For example, the original task asked students to work with some specific arguments (narratives); for example, ‘if you add 198 to 123, the sum becomes 321’ and ‘if you add 198 to 234, the sum becomes 432’. Through proving activities, these arguments were developed in a broader context and then general arguments were produced; for example., ‘if you add 198 to the three-digit numbers for which the difference of hundreds and ones is two, the sum becomes the number for which the digits are reversed’ (we called this argument NA2) and more general arguments as well (e.g. NA3 and NA4). Although these general arguments are still restricted to a given domain (i.e. the domain of three-digit integers), our findings implied an achievable degree of generality of the arguments for primary students.

Third, our theoretical approach can contribute to advancing some related theoretical frameworks proposed by different researchers. For example, Harel and Sowder’s (1998) classifications of proof schemes can be applicable (but not simply identical) to different types of proofs which were described as pre-formalist categories (see Section 2.4)¹⁰. Based on the synthesis by Reid and Knipping (2010, p. 149), some categories of ‘empirical’ and ‘analytical proof schemes’ can be mapped onto the types of proofs as showed in Table 3, although the ‘external proof scheme’ is not included (because this category cannot be associated with a certain type of proofs). For ‘subcategory 2’ in Table 3, a ‘generic proof scheme’¹¹ can be mapped onto the operative proof in our study. The generic proof scheme refers to ‘students’ inability to express their justification in general terms’ (Harel & Sowder, 1998, p. 271) and emphasizes the restriction of the generality of proving. However, the operative proof acknowledges the possibility of generality, even though this type of proof uses little symbolism (Wittmann, 2019, p. 29). Additionally, ‘[Harel and Sowder’s framework are] not the ways in which one type of understanding can develop into another’ (Ahmadpour et al., 2019, p. 86). We, therefore, described the transition between experimental and operative proofs in terms of the interplay between construction and substantiation of narratives (as summarized in Table 2).

Table 3. Proof schemes and types of proofs (adapted from Reid and Knipping (2010, p. 149)).

Category	Subcategory 1	Subcategory 2	Types of proofs
Empirical			Experimental
Analytical	Transformational	[Unrestrictive]	Formal
		Restrictive (generic)	Operative
	Axiomatic		Formal

Our findings can also support a recent study’s model of students’ ways of understanding a proof (Ahmadpour et al., 2019), which offered some theoretical pathways towards formally acceptable proof; for instance, generalisation (leads to a general procedure), abstraction (leads to an abstract structure), and formalisation (leads to a formulated proof). Although this model was examined by focusing on middle school students’ understanding of the process of reading a proof¹², our study implied that both generalization and abstraction are auxiliary but crucial processes to produce an operative proof by primary school students as well. In our analysis, as abovementioned, students began working with specific arguments, but they progressively underwent generalizations though producing more general arguments. For abstraction, one student’s insight of ‘the difference between the two numbers (the hundreds and the ones) is what you take away’ (in episode 3b) can be regarded as a critical event, referring to ‘a structure that “reifies” (Sfard, 1991) the underlying idea of a general procedure’¹³ (Ahmadpour et al., 2019, p. 93). In this way, our approach may advance Ahmadpour et al.’s model in the context of producing an operative proof.

5.4. Limitations for future research

Our study has three limitations. First, the role of gestures in the process of communication could have received greater attention (Sfard, 2009). Although we described a few aspects, the relation between gestures and other visual mediators (or other discursive aspects) was not given much attention. In terms of recent research on the multi-modality of proving (e.g. Campbell et al., 2020), it is worth investigating how gestures affect students’ proving activities. Second, our theoretical framing has not sufficiently considered the role of the teacher’s pedagogy, and their interventions were limited in this study. The form of teacher-student interaction may change over time. For instance, the teacher guided most of the students’ activity in the first episode, but more work was done by students in later episodes. S7 performed the task well with the teacher’s guidance and led other students’ use of the manipulatives. Teacher’s crucial role in facilitating students’ proving activity and its evolution should be addressed theoretically and practically. Third, concerning types of proofs, although our approach and task design based on operative proofs (Wittmann, 2009) might apply to the secondary school level, it is important to examine how it can be effective in secondary schools, aiming at further evolution in the understanding of mathematical proofs.

Acknowledgements

This work is supported by the JSPS KAKENHI (Grant Number JP17K04775 and JP20K02913).

Disclosure statement

No potential conflict of interest was reported by the authors.

Notes

1 The three perspectives were identified for use as an organising structure for the review; therefore, there seem to be some overlaps, but this only suggests the respective view of proving for each study may fit better than others (Stylianides et al., 2017). More recently, Campbell et al. (2019) utilised these perspectives for a more comprehensive review.

2 Jeannotte and Kieran (2017) define mathematical reasoning as a process of communication with others or with oneself that allows for inferring mathematical utterances from other mathematical utterances (p. 7)

3 Although Duval (2007) highlighted the difference between the epistemic value and the logical truth value, in this study, we follow Jeannotte and Kieran (2017), who stated that ‘from a discursive stand there is no difference between epistemic value and truth-value’ (p. 11).

4 This is a typical example that can be proven in different ways (e.g. Stylianides & Stylianides, 2008, p. 108). See also our descriptions about Figure 1.

5 Although the original literature, such as Wittman and Müller (1990), denotes experimental ‘proofs’ (the quotation marks imply a broader sense of proof), we call them experimental approaches (but still consider them one type of ‘proof’).

6 Wittmann (2009) stated, ‘At school level informal representations of mathematical objects are indispensable as they provide a ‘quasi-reality’ which is easily accessible. Patterns become in a sense ‘visible’ when informal representations like counters, the number line, the place value table, calculations with numbers and constructions of geometric figures are used’ (p. 255) [emphasis in original]

7 We did not include ‘what is done’ as a column in this episode as it does not seem necessary.

8 This summary was directly made from each episode, but it does not necessarily mean that a specific use of examples or type of proof has been shared in the classroom. For example, ‘particular and generic’ in uses of examples refers to the situation such that one student works on particular examples but another works on generic examples.

9 For example, in the second lesson (ANNA number), the students soon realized the underlying pattern (such as the differences between 3223-2332, 6556-5665 and so on, would be always 891), and explaining the reasons why using the manipulatives. More descriptions of operative proofs about ANNA number are mentioned by Wittmann (2019, pp. 27–29).

10 It is noted that Harel and Sowder’s (1998) research perspective is regarded as ‘proving as convincing’ (Stylianides et al., 2017), as mentioned at the beginning of this paper.

11 Harel and Sowder (1998) distinguished ‘restrictive proof scheme’ into further subcategories: ‘contextual’, ‘generic’, and ‘constructive’. In our interpretation, generic proof scheme is the most suitable category to be mapped onto the operative proof.

12 Ahmadpour et al. (2019) concluded that ‘[b]ecause of this interconnection [between reading and producing a proof], we developed our model with the expectation that it would be applicable also to students’ understanding in the process of producing a proof. The extent to which it can be used to describe proof production remains a question for future research’ (p. 103).

13 The notion of ‘reification’ (Sfard, 1991) has been reconceptualised within the commognitive framework (e.g. Güçler, 2016; Sfard, 2008; Shinno, 2018)