Acoustic properties and low strain rate behavior of different types of chocolate

ABSTRACT

Five different chocolate types (i.e. extra dark, dark, milk, white, and ruby) were characterized and compared for the acoustical and textural characteristics. Acoustic properties were described in terms of longitudinal and transversal wave velocities. These velocities were used for the evaluation of elastic constants namely Young modulus and Poisson ratio. The values of the Young moduli are significantly higher than those obtained using uniaxial compression and tensile tests. At the same time, the values of Poisson ratio are in reasonable agreement with results of these methods. Texture characteristics were evaluated using of the compression test at loading rates (crosshead velocity) 1, 10 and 100 mm/min. Results are presented in form of stress vs strain. The stress-strain dependences obtained from the compression test exhibited two different regions of the sensitivity of stress to the applied strain. The linear dependence stress- strain is taken as the evidence of the elastic behavior of the tested material. The extent of this region was given by the strain, which was the same for all tested chocolates. Its value increased with the loading rate. The stress-strain behavior in this region was only slightly dependent on the loading rate with exception of the ruby and dark chocolates. The stress-strain dependence in the following region was significantly dependent on the strain rate. Values of the strain rate sensitivity were evaluated. The order of the tested chocolates according to the values of stress at the given strain was identical with that obtained using of the elastic wave velocities.

KEYWORDS:

• Chocolate
• elastic wave
• compression
• strain hardening
• young modulus
• strain rate sensitivity

Introduction

Chocolate is defined as a semi-solid suspension, made of sugar and cocoa (in the form of fine solid particles) disperse in fat phase of cocoa butter. The structure of the chocolates is very complex. Cocoa butter is polymorphic with 6 ways of crystalline forms designated as polymorphs I–VI (structurally different with same chemically identical).^[1] C-2: References should be number format Dark, milk and white chocolate are the three main types that differ in the content of cocoa solids, milk fat and cocoa butter. This is the reason for the different contents of fats, carbohydrate and proteins.^[2] In 2017, the Belgian-Swiss company Barry Callebaut brought to the world market ruby chocolate which is still waiting to be approved as the fourth type of chocolate.^[3]

Rheological and textural properties of the three types of chocolate were studied in many papers, see e.g.^[4,5] The rheological properties of chocolate are very important for the production of high-quality products with a well-defined texture.^[6] Textural properties represent one of the three main acceptability factors, in addition to appearance and flavor, that consumers use to evaluate chocolate quality. The texture is examined using sensory evaluation or by instrumental methods, see e.g.^[7] A commonly used method of measuring the textural properties of foods is the compression test based on the similarity to the chewing effect in the mouth. The meaning of this test for the understanding of the chocolate behavior during the oral processing is described, e.g. by.^[8] The comprehensive data on the chocolate behavior during the compression test were obtained by.^[9] These dates are also needed for the development of chocolate constitutive equation, which can be used in computational models enabling the numerical simulation of the oral process. The next advantages of the uniaxial compression test are that it does not require creating a specific sample shape or size and does not require attaching the sample to the test apparatus. This test has been applied to investigate hardness^[10] as well as chocolate texture as a function of composition, fat content or storage conditions^[11–13,14]. The aim of this paper consists in the detail analysis of the behavior of different types of chocolates (extra dark, dark, milk, white, ruby) during the compression test. The values of used strain rates are relevant to lower values of the strain rates occurring during the mastification, which lies between 0.1 and 2.5s⁻¹ as reported, e.g. by.^[15] In order to obtain some more detail view on the chocolate properties, the basic acoustics properties have been also evaluated.

Material and experimental procedure

Material

Five chocolate masses were used for the experiments – extra dark chocolate (EDC), dark chocolate (DC), milk chocolate (MC), white chocolate (WC), and ruby chocolate (RC). The EDC (Domori, Italy) contains 100% cocoa components (Morogoro, Tanzania). The DC, MC, and WC (Belcolade, Switzerland) contain 55.5%, 36.5%, and 28% cocoa components. The RC (Callebaut, Belgium) contains 47.3% cocoa components. Further characteristics (nutritional data) of these chocolate masses are given by.^[16] The specimens of cylindrical shape (14 mm in diameter and 7 mm in height) have been prepared.

Acoustic properties

The acoustic properties characterized by velocities of the longitudinal wave and transversal wave were measured. The velocities of the longitudinal wave c_L and transversal wave c_T were measured ultrasonically by pulse echo method using µDiSP system (Physical Acoustics Corporation, NJ, USA). The longitudinal wave velocity was determined with 3.5 MHz Gamma probe (Aerotech, Czech Republic), the transversal velocity was determined with normal incidence shear wave transducer V154 (Olympus, Japan) operating at 2.25 MHz. The knowledge of these velocities enables to evaluate the elastic behavior of the tested material in terms of Poisson’s ratio ν (Equation 1a(1a) $\nu =\frac{c_L^2-2c_T^2}{2\left(c_L^2-c_T^2\right)},$(1a) ), Young’s modulus E (Equation 1b(1b) $E=2\rho c_T^2\left(1+\nu \right),$(1b) ), shear modulus G (Equation 1c(1c) $G=\frac{E}{2\left(1+\nu \right)},$(1c) ), and bulk modulus K (Equation 1d(1d) $K=\frac{E}{3\left(1-2\nu \right)},$(1d) ) according to the relations^[17]:

(1a) $\nu =\frac{c_L^2-2c_T^2}{2\left(c_L^2-c_T^2\right)},$(1a)

(1b) $E=2\rho c_T^2\left(1+\nu \right),$(1b)

(1c) $G=\frac{E}{2\left(1+\nu \right)},$(1c)

(1d) $K=\frac{E}{3\left(1-2\nu \right)},$(1d)

where ρ is the material density.

Uniaxial compression test

The compression tests were conducted using of TIRATEST 27,025 testing machine (TIRA Maschinenbau, Germany). A cylindrical sample of height l_o and cross section A_o is compressed between two parallel metal plates at a fixed crosshead speed v. The force F and the compression $\mathrm{\Delta }l=vt$ are measured during compression and both quantities are recorded. The force-deformation data may easily be transformed into normalized quantities such as stress and strain. The Cauchy or engineering strain and Hencky’s natural or “true” strain are of common use in representing compression curves.^[18] The Cauchy strain measure, ε gives the relative deformation with respect to the initial sample height l₀:

(2) $\epsilon =\frac{\mathrm{\Delta }l}{l_o}.$(2)

Hencky’s strain ε_H (often denoted as “true” strain) derives from the integration of the infinitesimal strain $-\frac{dl}{l}$ and reads:

(3) ${\epsilon }_H\equiv {\epsilon }_{true}=-ln\left(\frac{l_o-\mathrm{\Delta }l}{l_o}\right)=-ln\left(1-\epsilon \right).$(3)

The force F can be converted to the ultimate or engineering stress σ and/or to the true stress σ_true. The ultimate (engineering) stress is simply given as:

(4) $\sigma =\frac{F}{A_o}$(4)

The true stress is evaluated using of the instantaneous cross section A. Its value is mostly obtained using assumption on the constant volume of the specimen^[19]:

(5) $V=V_0\iff Al=A_0{l}_0;A=A_0\frac{l_0}{l}=A_0\frac{l_0}{\left(l-\mathrm{\Delta }l\right)}$(5)

The true stress is than expressed as:

(6) ${\sigma }_{true}=\frac{F}{A}=\frac{F}{A_o}\frac{l_o-\mathrm{\Delta }l}{l_o}\iff {\sigma }_{true}=\sigma \left(1-\epsilon \right).$(6)

The engineering strain rate is given as:

(7) $\dot{\epsilon }=\frac{d\epsilon }{dt}=\frac{v}{l_o}.$(7)

The true strain rate can be expressed as:

(8) ${\dot{\epsilon }}_{true}\equiv \frac{d{\epsilon }_{true}}{dt}=\frac{1}{1-\epsilon }\frac{d\epsilon }{dt}=\frac{v}{l_o\left(1-\epsilon \right)}.$(8)

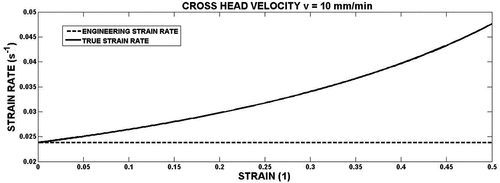
Compression tests were performed at the crosshead speeds (loading rates) 1, 10 and 100 m/s. For each loading rate, the test was repeated five times. To these loading rates correspond the constant engineering strain rates, see Equation (7)(7) $\dot{\epsilon }=\frac{d\epsilon }{dt}=\frac{v}{l_o}.$(7) : 0.0024, 0.024 and 0.24 s⁻¹. Specimens were compressed approximately to one half of the specimen length, i.e. to engineering strain 0.5. During the compression, the true strain rate increases. Example of the dependence ${\dot{\epsilon }}_{true}=f\left(\epsilon \right)$ is shown in the Figure 1. For each specimen, force displacement data were logged with time and were converted to stress-strain data using Equations. (2)(2) $\epsilon =\frac{\mathrm{\Delta }l}{l_o}.$(2) , (3(3) ${\epsilon }_H\equiv {\epsilon }_{true}=-ln\left(\frac{l_o-\mathrm{\Delta }l}{l_o}\right)=-ln\left(1-\epsilon \right).$(3) ), (4(4) $\sigma =\frac{F}{A_o}$(4) ) and (6(6) ${\sigma }_{true}=\frac{F}{A}=\frac{F}{A_o}\frac{l_o-\mathrm{\Delta }l}{l_o}\iff {\sigma }_{true}=\sigma \left(1-\epsilon \right).$(6) ). All compression tests as well as the measurement of acoustics properties were performed at the temperature 10°C.

Figure 1. The dependence of the true strain rate on the engineering strain for white chocolate.

Statistical analysis

The experimental data were processed by MATLAB R2018b (MathWorks, Natick, MA, USA), which includes moduli for the statistical analysis and curve fitting. An analysis of variance (ANOVA) using a 95% significance level was employed to identify significant differences between the different types of chocolate. The results were presented as averages.

Results and discussion

Acoustic properties

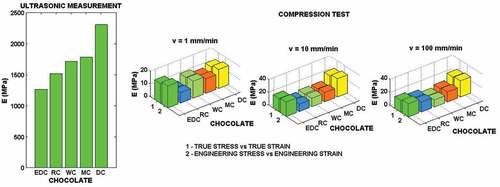
The results of density, velocities of the longitudinal wave c_L and transversal wave c_T of chocolate are given in the Table 1. Theoretical values of elastic properties of chocolate evaluated using of Equations (1a(1a) $\nu =\frac{c_L^2-2c_T^2}{2\left(c_L^2-c_T^2\right)},$(1a) -1d(1d) $K=\frac{E}{3\left(1-2\nu \right)},$(1d) ) are given in the Table 2. According to the value of longitudinal wave velocity, the order of the different types of chocolate since minimum to maximum value is:

(9) $EXTRA\hspace{0.17em}DARK\to RUBY\to WHITE\to MILK\to DARK$(9)

Table 1. Acoustical properties of the tested chocolates.

Chocolate	ρ (kg/m^3)	cL (m/s)	cT (m/s)
DC	1269.4	2208	798
MC	1263.4	2106	700
WC	1252.8	2094	649
RC	1244.8	2074	611
EDC	1170.0	1982	689

Table 2. Elastic properties of the tested chocolates.

Chocolate	E (MPa)	ν	G (MPa)	K (MPa)
DC	2303.6	0.4243	803.36	3110.8
MC	1780.3	0.4373	619.07	4778.1
WC	1712.0	0.4393	594.73	4700.3
RC	1516.0	0.4457	524.31	4655.4
EDC	1264.5	0.4475	436.79	4013.8

If we use the values of transversal stress wave the order of chocolates is:

(10) $RUBY\to WHITE\to EXTRA\hspace{0.17em}DARK\to MILK\to DARK$(10)

The order of chocolates according to the values of elastic moduli E, G a K is given by relation (9).

Compression loading

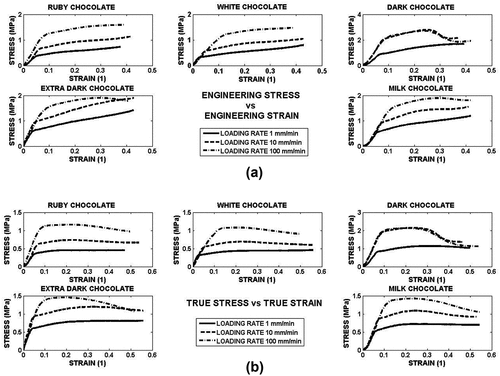
In the Figure 2, example of compression curve in terms of stress versus strain is displayed. It is obvious that the true stress is lower than the engineering stress. Owing to the dependence of the true strain on the strain rate the dependence of the true stress on the true strain should be expressed as 3D curve, see the lower part of the Figure 2. The stress-strain curves for all used loading velocities and chocolates are presented in the Figures 3(a-c).

Figure 2. Example of the stress-strain curve for white chocolate. The difference between engineering and true stress strain dependences is shown in the upper part of the figure. The lower part shows the loading history of the specimen in the space strain-strain rate – stress.

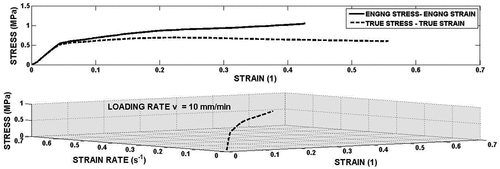
Figure 3. (a.) Stress-strain curves at loading rate 1mm/min, (b.) Stress-strain curves at loading rate 10mm/min, (c.) Stress-strain curves at loading rate 100mm/min.

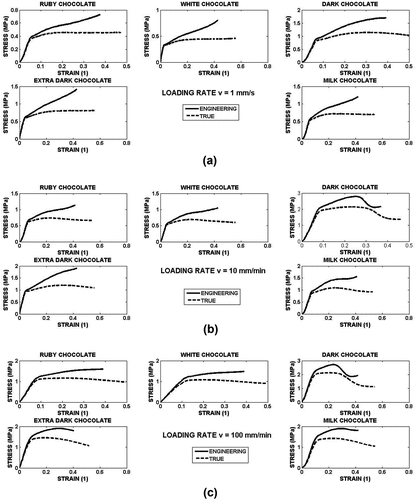
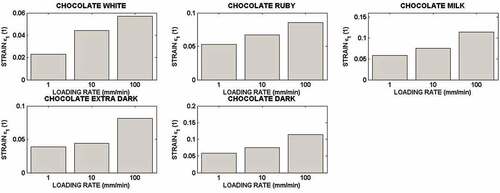
All curves exhibit two regionss of the stress-strain dependence. Some exception one can observe for the dark chocolate where some decrease of the stress at the end of compression occurs. In the first region $\epsilon \le {\epsilon }_1$ , the stress rapidly increases with the strain. The difference between engineering stress and true one is very small, if not negligible. The extent of this region given by strain increases with the loading rate as it is shown in the Figure 4. The analysis of these data shows that there is no statistically significant difference among tested chocolates. This limit strain ε₁ increases with the loading rate.

Figure 4. Effect of loading rate on the extent of the first region of the stress-strain curve.

The difference between engineering and true stress is significant in the following region where the stress-strain curve exhibits much smaller steepness in comparison with the region I. This character of the stress strain curve is typical for many engineering materials.^[20] The first region is commonly interpreted as the region of elastic strain where the stress depends on the strain linearly. The second region is than connected with the permanent strain and other not reversible structure changes of the specimen material. The detail analysis of the curves in region I shows that the stress increases linearly with strain as:

(11) $\sigma =a+b\epsilon .$(11)

This equation is valid both for the engineering and true values of stress and strain. Coefficients of Equation (11)(11) $\sigma =a+b\epsilon .$(11) are given in the Tables 3 and 4.

Table 3. Parameters of linear function describing the engineering stress vs engineering strain dependence in the first region.

Chocolate	v (mm/min)	a (MPa)	b (MPa)	R^2	ε1 (1)
WC	1	−0.0348 ± 0.0004	13.2 ± 0.2	0.9964	0.023 ± 0.001
	10	−0.0298 ± 0.0002	12.9 ± 0.2	0.9964	0.0443 ± 0.0003
	100	−0.00077 ± 0.00005	10.8 ± 0.5	0.9989	0.0571 ± 0.0002
RC	1	−0.0355 ± 0.0007	8.1 ± 0.2	0.9917	0.05 ± 0.07
	10	−0.0905 ± 0.0008	11.6 ± 0.3	0.9812	0.0671 ± 0.0009
	100	0.00037 ± 0.00001	15.0 ± 0.2	0.9913	0.0857 ± 0.0008
MC	1	−0.100 ± 0.001	11.2 ± 0.2	0.9697	0.059 ± 0.001
	10	−0.127 ± 0.003	14.4 ± 0.3	0.9809	0.076 ± 0.002
	100	−0.181 ± 0.006	15.2 ± 0.4	0.9807	0.114 ± 0.007
EDC	1	0.024 ± 0.003	17.1 ± 0.2	0.9932	0.039 ± 0.002
	10	0.036 ± 0.007	22.3 ± 0.4	0.9964	0.0443 ± 0.0003
	100	−0.017 ± 0.001	20.2 ± 0.5	0.9985	0.0814 ± 0.0002
DC	1	−0.121 ± 0.005	14.8 ± 0.4	0.9750	0.059 ± 0.002
	10	−0.183 ± 0.004	28.2 ± 0.4	0.9932	0.076 ± 0.002
	100	−0.074 ± 0.004	24.7 ± 0.5	0.9304	0.114 ± 0.004

Table 4. Parameters of linear function describing the true stress vs true strain dependence in the first region.

Chocolate	v (mm/min)	a (MPa)	b (MPa)	R^2	ε1 (1)
WC	1	0.0258 ± 0.0004	12.5 ± 0.6	0.9901	0.025 ± 0.002
	10	−0.0277 ± 0.0002	12.4 ± 0.4	0.9967	0.045 ± 0.001
	100	0.016 ± 0.002	9.5 ± 0.4	0.9973	0.092 ± 0.001
RC	1	−0.0303 ± 0.0007	7.5 ± 0.4	0.9952	0.053 ± 0.002
	10	−0.0802 ± 0.0008	10.7 ± 0.8	0.9883	0.060 ± 0.001
	100	−0.0048 ± 0.0001	14.3 ± 0.6	0.9965	0.074 ± 0.001
MC	1	−0.088 ± 0.001	10.0 ± 0.2	0.9670	0.056 ± 0.004
	10	−0.105 ± 0.003	12.7 ± 0.5	0.9755	0.0664 ± 0.0007
	100	−0.144500 ± 0.0007	13.2 ± 0.2	0.9734	0.10 ± 0.06
EDC	1	0.039 ± 0.003	15.2 ± 0.1	0.9932	0.0364 ± 0.0007
	10	0.053 ± 0.003	20.4 ± 0.5	0.9947	0.043 ± 0.001
	100	0.0125 ± 0.0003	17.8 ± 0.3	0.9958	0.6950 ± 0.0005
DC	1	−0.0943 ± 0.0008	13.0 ± 0.3	0.9764	0.604 ± 0.001
	10	−0.1437 ± 0.0003	25.1 ± 0.3	0.9941	0.074 ± 0.004
	100	−0.073 ± 0.003	23.0 ± 0.4	0.9937	0.085 ± 0.002

Parameter b gives the slope of the initial linear region. This slope defines the material property known as the Young modulus E.^[21] This moduli is defined as:

(12) $E={\frac{d\sigma }{d\epsilon }}_{\epsilon =0}.$(12)

It means that this moduli is equal to parameter b in the Equation (11)(11) $\sigma =a+b\epsilon .$(11) , thus E ≡ b. The values of moduli E are displayed in the Figure 5. Analysis of these data shows that there is no statistically significant difference among chocolates Ruby, Extra Dark, Milk and White. Significant difference was found for the dark chocolate. Its E moduli is higher than that for remaining tested chocolate. The moduli E evaluated from the engineering stress-engineering strain curves are slightly higher than those evaluated from the true stress-true strain curves.

Figure 5. Parameters of non linear function describing the dependence true stress vs true strain in the second region.

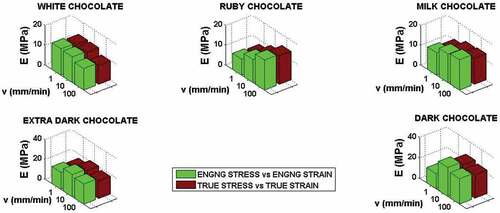
The values of E moduli found in the given paper are lower than those obtained by^[9] from the compression tests performed at similar strain rates as in the present paper. Our results are similar to those reported by.^[21] In this paper, results of tensile uniaxial tests are presented. All elastic moduli obtained from the uniaxial stress loading are significantly lower than those obtained from the acoustical properties using Equation (1b)(1b) $E=2\rho c_T^2\left(1+\nu \right),$(1b) . This discrepancy was also reported for watermelon flesh – see.^[22] The values of the Poisson ratio νis similar to that obtained from the uniaxial tension test.^[21] E moduli found for chocolates white, ruby and milk exhibit an increase with the loading rates (Figure 6).

Figure 6. Parameters of linear function describing the engineering stress vs engineering strain dependence in the second region.

This behavior is typical for viscoelastic materials. The viscoelastic properties of the milk chocolate were reported in paper of.^[9] In this paper, the constitutive equation describing the viscoelastic behavior of the chocolate was developed. The validity of this equation is limited to relatively small strain rates. Its extension to higher strain rates represents a problem of the next study.

The effect of the loading rate on the stress-strain curves is illustrated in the Figure 7a (engineering stress and strain) and in the Figure 7b (true stress-true strain). It is evident that in the region where the stress increases with strain linearly $\epsilon \le {\epsilon }_1,$ is this rate dependence significantly lower than that for larger strains. The true stress versus true strain in this region $>{\epsilon }_1$, is fitted by non-linear function:

(13) ${\sigma }_{true}=a_4{\epsilon }_{true}^4+a_3{\epsilon }_{true}^3+a_2{\epsilon }_{true}^2+a_1{\epsilon }_{true}+a_0,$(13)

Figure 7. (a.) Effect of the loading rate on the stress vs strain dependence – engineering approach, (b.) Effect of the loading rate on the stress vs strain dependence – true values of stress and strain.

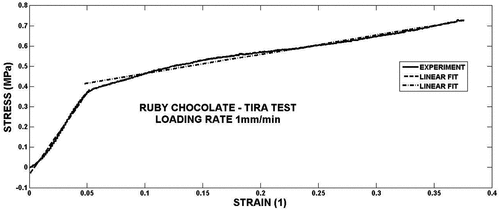
Values of coefficients of Equation (13)(13) ${\sigma }_{true}=a_4{\epsilon }_{true}^4+a_3{\epsilon }_{true}^3+a_2{\epsilon }_{true}^2+a_1{\epsilon }_{true}+a_0,$(13) are given in the Table 5. The data engineering stress-engineering strain can be for some cases also fitted by linear function, see Figure 8 as an example. The linear approximation may be used for the most of experimental records σ (ε). The parameters of the linear functions (Equation 11(11) $\sigma =a+b\epsilon .$(11) ) in region $\epsilon >{\epsilon }_1$ are given in the Table 6. The sensitivity of the stress to the strain rate is given as:

(14) ${\frac{d\sigma \left(\epsilon \right)}{d\dot{\epsilon }}}_{\epsilon =const}.$(14)

Figure 8. Example of linear fit of engineering stress vs engineering strain.

Table 5. Best fittings parameters of Equation (13)(13) ${\sigma }_{true}=a_4{\epsilon }_{true}^4+a_3{\epsilon }_{true}^3+a_2{\epsilon }_{true}^2+a_1{\epsilon }_{true}+a_0,$(13) and determination coefficients (R²) for true stress – true strain.

Chocolate	v (mm/min)	a4 (MPa)	a3 (MPa)	a2 (MPa)	a1 (MPa)	a0 (MPa)	R^2
WC	1	0	3.529	−3.889	1.403	0.2789	0.9957
	10	0	7.050	−8.540	2.641	0.3636	0.9888
	100	−104.400	146.100	−74.690	15.760	−0.0678	0.9973
RC	1	−20.852	28.323	−13.881	2.895	0.2373	0.9972
	10	−5.436	14.491	−11.342	3.167	0.4447	0.9769
	100	−25.362	36.599	−20.717	4.686	0.8053	0.9755
MC	1	−17.608	29.073	−17.573	4.506	0.3066	0.9972
	10	22.697	−12.099	−6.136	3.929	0.5849	0.9926
	100	−28.140	52.491	−36.457	9.673	0.5798	0.9828
EDC	1	−1.186	6.0073	−6.235	2.381	0.4985	0.9882
	10	14.148	−14.693	1.735	1.595	0.8423	0.9980
	100	−57.320	80.315	−43.227	9.328	0.7785	0.9863
DC	1	12.390	−8.514	−4.036	3.486	0.5894	0.9963
	10	459.028	−455.404	138.156	−13.985	2.3437	0.9815
	100	289.523	−276.882	72.784	−4.834	1.9677	0.9907

Table 6. Best fittings parameters of Equation (11)(11) $\sigma =a+b\epsilon .$(11) in the region $\epsilon >{\epsilon }_1$and determination coefficients (R²). Engineering stress-Engineering strain.

Chocolate	v (mm/min)	a (MPa)	b (MPa)	R^2
WC	1	0.32 ± 0.03	1.08 ± 0.07	0.9922
	10	0.59 ± 0.01	1.15 ± 0.01	0.9326
	100	1.15 ± 0.02	0.92 ± 0.01	0.9915
RC	1	0.37 ± 0.02	0.95 ± 0.02	0.9819
	10	1.15 ± 0.01	1.36 ± 0.01	0.9870
	100	0.55 ± 0.01	1.58 ± 0.01	0.9750
MC	1	0.95 ± 0.03	1.61 ± 0.08	0.9809
	10	0.57 ± 0.01	2.01 ± 0.03	0.9930
	100	0.83 ± 0.01	3.02 ± 0.02	0.9968
EDC	1	0.80 ± 0.01	2.62 ± 0.10	0.9498
	10	0.320 ± 0.002	1.08 ± 0.05	0.9922
	100	0.587 ± 0.005	1.1 ± 0.4	0.9326
DC	1	1.147 ± 0.006	0.92 ± 0.07	0.9915
	10	0.370 ± 0.002	0.95 ± 0.01	0.9819
	100	1.151 ± 0.008	1.36 ± 0.05	0.9870

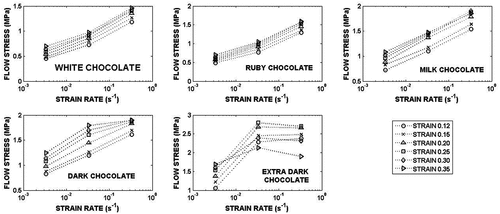
The procedure of the strain rate sensitivity is thus based on the dependence stress versus strain rate for a given value of strain. In this paper, we obtain data for the three values of strain rates. In the Figure 9, the points stress vs strain rates are plotted. The used values of strain are higher than the maximum value of strain ε₁.

Figure 9. Stress vs strain rate for different values of strain.

Owing to limited number of used strain rates, it is impossible to evaluate parameter according to Equation (14)(14) ${\frac{d\sigma \left(\epsilon \right)}{d\dot{\epsilon }}}_{\epsilon =const}.$(14) . For chocolates: white, ruby and milk, the stress increases with strain rate. The value of stress is increased by the factor about three. Experimental data suggest the possible dependence $\sigma \sim ln\left(\dot{\epsilon }\right)$. The increase in the stress with strain rate for the dark chocolate is very similar with exception of higher values of strain. The dependence stress versus strain rate observed at chocolate extra dark exhibits another features. This is a consequence of the different shape of the stress-strain curve in comparison with remaining types of chocolate. The data describing the strain rate sensitivity were obtained from the data engineering stress versus engineering strain. The conclusions following from the data true stresstrue strain are qualitatively the same.

Conclusion

In the given paper, the behavior of five types of chocolate under quasi-static compression at three values of loading rate. The experiments were evaluated using both engineering stress-strain as well as true stress-strain curves. The curves exhibit two region of the deformation behavior. In the first region, since zero to some value of strain, the stress is linear function of the strain. The extent of this region is independent on the type of tested chocolate. The extent of this region increases with the loading rate. The stress in this region is only slightly dependent on the strain rate. Similarly as in some up to known works the slope of the stress-strain curve in the first region can be taken as the Young modulus E. The highest value of this modulus was obtained for the Dark chocolate. The values of elastic moduli for remaining chocolates are the same. These conclusions are the same both for engineering approach as well as for the true stress-strain representation. The obtained elastic moduli are significantly lower than those reported in some up to known papers. The values of this modulus are much lower than those obtained from the results of ultrasonic tests. This discrepancy may be given by the viscoelastic behavior of the tested chocolates. This hypothesis may be verified by the use of stress relaxation tests. At the same time, the results of the ultrasonic tests gives value of the Poisson ratio similar to that obtained from the compression test. In the second region, the increase of stress with strain is significantly lower than that in the first region. The sensitivity stress to the strain rate in the given region is much higher than that in the first region. The stress is mostly non-linear function of the strain. From this point of view, the strain behavior of tested chocolates during the compression exhibited very similar features like strain behavior of the most engineering materials (metals, polymers, etc.).

Ethical Review

This study does not involve any human or animal testing.

Informed consent

Written informed consent was obtained from all study participants.

Acknowledgments

This research was supported by the Internal Grant Agency of the Faculty of AgriSciences no. AF-IGA-2020-TP006 “Modelling of rheological properties of liquid and semi-liquid food raw materials and foods showing non-Newtonian behaviour” and by the European Regional Development Fund under Grant No. CZ.02.1.01/0.0/0.0/15_003/0000493 (Centre of Excellence for Nonlinear Dynamic Behaviour of Advanced Materials in Engineering).

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

The work was supported by the AF-IGA-2020-TP006 “Modelling of rheological properties of liquid and semi-liquid food raw materials and foods showing non-Newtonian behaviour” European Regional Development Fund under Grant No. CZ.02.1.01/0.0/0.0/15_003/0000493.