Modelling early childhood teachers’ mathematics-specific professional competence and its differential growth through professional development – an aspect of structural validity

ABSTRACT

Research on teacher knowledge has been criticised for taking too narrow a view on expertise. Therefore, teacher competence frameworks have been developed that are closely related to professional demands. Their practice-oriented conceptualisations have led to innovative measures with situative demands. However, there is still a lack of knowledge on whether these frameworks are actually suited to map teacher growth. This study investigated whether two components of teacher competence, Action-related (AC) and Reflective Competence (RC), can be differentially fostered through specific interventions in early childhood mathematics education. We designed two professional development programmes with a focus on AC and RC and implemented them in a randomised controlled experiment with 170 teachers. Overall, we found that AC, RC, and professional knowledge were sensitive to interventions with different change profiles. Although our hypotheses were only partially supported, the results can be seen as evidence regarding the distinctness of competence and knowledge components.

KEYWORDS:

• Teacher competence
• early mathematics
• experimental study

A response to the criticism that prevalent teacher knowledge research often takes a too narrow view on teacher expertise is the use of teacher professional competence frameworks (see Section 1.1). Professional competence is understood here as the cognitive dispositions required to master professional demands.¹ These frameworks are strongly oriented towards the professional demands of teaching a subject and therefore often use situated assessment. The teacher competence model of Lindmeier (2011), initially developed for secondary mathematics teachers, differentiates, for example, between the in-instructional and pre-/post-instructional demands of teaching a subject and is already used in different contexts, including early childhood mathematics education. The model builds on innovative video-based and (partly) timed items, and first successful applications have already been reported (see Section 1.2). However, as these approaches are still evolving, sound knowledge of whether they fulfill the intended purposes is lacking, for example, concerning the tracing of effects of professional development (see Section 1.3). Above all, there is still a lack of evidence on whether teacher competence measures respond in a differentiated way to teacher growth, so that the theoretical structuring of competence can also be empirically validated. The present study addressed this gap and investigated whether two competence components related to different instructional demands can be differentially fostered through specific interventions in the context of early childhood education. This study hence focused on the structural validity aspect of the teacher competence assessment approach (AERA, APA, & NCME, 2014).

1. From teacher knowledge to teacher competence

Teacher knowledge has become an important area of research in the last decades. The seminal differentiation between Content Knowledge (CK) and Pedagogical Content Knowledge (PCK; Shulman, 1986) sparked an area of research on the components of teacher (subject-specific) knowledge.

Different frameworks were developed to specify CK and PCK. For example, Baumert et al. (2010) conceptualised PCK with the help of the facets knowledge of tasks, knowledge of student ideas, and knowledge of representations and explanations. For mathematical knowledge, Hill, Schilling, and Ball (2004) differentiated profession-specific mathematical knowledge (Specialised Content Knowledge, SCK) from a general CK. Others describe CK and PCK for certain content areas (e.g. rational numbers, Depaepe et al., 2015) or even topics (e.g. area of a trapezoid, Martinovic & Manizade, 2018). Teacher knowledge models often reflect normative aspects, and are therefore also used to compare education systems (Blömeke & Delaney, 2014) and to analyse frameworks of university-based teacher education (Dreher, Lindmeier, Heinze, & Niemand, 2018).

Empirical research provided important findings on the structure of mathematics teachers’ knowledge, its development in teacher education, and international differences in initial teacher education. However, teacher knowledge models are still criticised. The following arguments can be summarised:

1. Many frameworks understand CK and PCK in the sense of declarative, decontextualised, abstract knowledge (Depaepe, Verschaffel, & Kelchtermans, 2013), but teachers’ knowledge cannot be exhaustively described as such. It also encompasses other knowledge sources, which might be inert or of a different quality (e.g. Putnam & Borko, 2000; Shulman, 1986). Hence, research should use broader understandings of knowledge, considering, for example, that knowledge of practitioners is related to cases (Putnam & Borko, 2000).

2. Although teacher knowledge is the base, teachers’ actual decision-making is the crucial point of teacher expertise (e.g. Westerman, 1991). Most conceptualisations and operationalisations of teacher knowledge refer to practical tasks, job analyses, or demands of teaching (e.g. Hill et al., 2004), but knowledge (as elicited in a teacher knowledge test) may be inert in actual decision making. Hence, research should account for the usability of knowledge in relevant decision-making processes (e.g. Blömeke, Gustafsson, & Shavelson, 2015; Kersting, Givvin, Thompson, Santagata, & Stigler, 2012).

3. Teaching can be considered to be a problem-solving process, where rational, reasoned decision-making processes, as well as quick, intuitive decisions, are needed (e.g. Schön, 1983/2002). Dual processing models of cognition suggest that successful problem solving relies on different memory and reasoning systems depending on the vastly different contextual affordances (e.g. Evans, 2008), in short, slow and fast thinking.² Whereas slow-thinking processes often draw on declarative knowledge and deliberate rational behaviour, fast-thinking processes often rely on familiarity with situations and related practices. Research should hence account for the different slow and fast demands of problem solving in teaching.

Although synthesised from different lines of research, these arguments share a common core: that narrowing teacher expertise down to professional knowledge might not be sufficient to explain observed teacher behaviour. The criticism might particularly be relevant when it comes to assessing the growth of teachers’ expertise, for example, in Professional Development (PD) or in programmes with an emphasis on preparation for practice instead of on the development of decontextualised professional knowledge.

One approach developed to address these challenges uses a model of teacher professional competence (Knievel, Lindmeier, & Heinze, 2015; Lindmeier, 2011) intended to complement prevailing models of teacher professional knowledge. This approach is in line with other attempts to extend the understanding of PCK towards contextualised (Ruthven, 2011) or professionally situated (Manizade & Mason, 2011) teacher knowledge. But, unlike others, it uses the concept of competence (in a dispositional understanding) to avoid the further blurring of the PCK construct and, additionally, applies dual processing theories of cognition to address the observed challenges.

1.1. Being prepared to master professional demands as a touchstone of professional competence

Competence constructs originated from the desire to address discrepancies between tests of isolated traits (e.g. knowledge) and the complex demands of real-life performance (Blömeke et al., 2015). Different understandings evolved, especially as to whether competences should be understood as the cognitive characteristics (cognitive dispositions) of the person that cause high performance on criterion tasks, or as the performance of the person on criterion tasks (McMullan et al., 2003). Following the dispositional perspective, we understand competences as “complex ability constructs that are context-specific, trainable and closely related to real life” (Koeppen, Hartig, Klieme, & Leutner, 2008, p. 61). In our case, the mathematics-specific professional demands of teachers constitute the real-life criterion tasks. Competences hence encompass different knowledge sources, skills (e.g. noticing, decision-making), and affective-motivational characteristics, which are knit together in a way demanded by the profession, and they are understood as prerequisites for high performance in dealing with the relevant professional demands (Blömeke et al., 2015).

Lindmeier (2011) argued that two fundamentally different types of professional demands must be distinguished: (1) pre- and post-instructional demands that allow for analytical, reasoned decision-making processes, and (2) in-instructional demands that require teachers to act in the moment (Schön, 1983/2002) and hence to rely on quick, intuitive decision-making processes. Dual processing theories of the mind (e.g. Evans, 2008) suggest that mastering these fundamentally different demands requires differently tailored cognitions, as these demands refer to fast- and slow-thinking processes. In the context of school teachers, this distinction was first used by Lindmeier (2011) to introduce two components of competence: Action-related Competence (AC), which refers to the cognitive dispositions required to master subject-specific demands in instruction, and Reflective Competence (RC), which refers to the cognitive dispositions required to master the subject-specific demands of pre- and post-instructional tasks (Figure 1). In line with the dispositional view of competence, professional knowledge (i.e. both CK and PCK) is the basis for AC and RC, which means that the teacher competence model complements research on teacher knowledge. According to the theory, RC is expected to be more closely related to teacher professional knowledge than AC, as solving slow demands of teaching allows for processes of knowledge deliberation.

Figure 1. Model of teacher competence (adapted from Lindmeier, 2011).

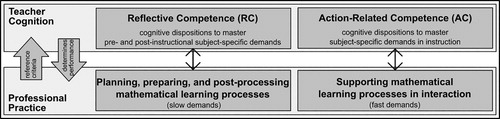
The teacher competence model addresses the issues of teacher knowledge research discussed above: (I) The touchstone of competence is whether teachers are equipped to master certain professional demands and not whether they possess (potentially inert) professional knowledge. (II) In contrast to some teacher knowledge models, the competence model allows for further resources, such as decision-making skills or motivational factors, to play out. (III) The differentiation between fast and slow demands according to dual cognition theories is fundamental to the model. The model hence has the potential to address the challenges outlined above.

Operationalisations of this model mirror the key characteristics of AC and RC, including fast and slow demands (Jeschke et al., 2019; Knievel et al., 2015). Measures of AC use time constraints and videos of real-life situations as stimuli and ask the teachers to act as if they were in the situation presented in the videos, thereby capturing the reactions in a naturalistic answer format. This approach led to a high face validity in studies with different teachers (Hepberger, Moser Opitz, Heinze, & Lindmeier, 2019; Knievel et al., 2015; Lindmeier, 2011). In contrast, the assessment of RC aims to stimulate analytical reasoning processes that are related to mathematical learning situations, mirroring tasks of the planning or post-processing of instruction. Videos or written vignettes similarly represent real-life situations. But prompts and assessment modes differ according to the nature of RC: The teachers have to diagnose student’s thinking or analyse the mathematical affordances of situations or materials. To ensure an engagement in slow cognitive processes, the assessment of RC typically does not use any time limitations and uses a written answer format (Knievel et al., 2015).

Previous research findings obtained by using this approach have shown that AC and RC can be empirically distinguished from professional knowledge, although RC is usually related to professional knowledge more closely than AC. This is in line with theoretical assumptions and supports aspects of structural evidence (Jeschke et al., 2019; Knievel et al., 2015; Lindmeier, 2011). Further, Jeschke et al. (2019) investigated the professional competence of mathematics and economics teachers in a domain-comparing approach and their findings support the generalisability of the model across domains. To sum up, the teacher competence model has led to a more differentiated view on teacher expertise and empirical studies have supported the viability of the approach.

1.2. Professional competence of early childhood teachers

Children develop their knowledge and abilities in numbers and basic operations during kindergarten age (4–6 years), and these early mathematical abilities predict later achievement in mathematics (e.g. Krajewski & Schneider, 2009). In contrast to the school context, mathematical learning opportunities in kindergarten are often connected to play or everyday situations, or are not clearly marked as learning opportunities (Samuelsson & Carlsson, 2008). This is especially apparent in countries where kindergarten is understood to be part of the early education and care system and, hence, different from school (e.g. Germany; Gasteiger, 2012). The importance of mathematical learning opportunities in kindergarten is underpinned by research (e.g. Stebler, Vogt, Wolf, Hauser, & Rechsteiner, 2013).

Research has also shown that early childhood teachers play an essential role by planning, offering, and supporting mathematical learning (Klibanoff, Levine, Huttenlocher, Vasilyeva, & Hedges, 2006; Lee & Ginsburg, 2009). The teacher has to provide apt learning opportunities and support the child’s learning, for example, through scaffolding (van de Pol, Volman, & Beishuizen, 2010). Similar to school teachers, it is emphasised that early childhood teachers need high CK and PCK as well as diagnostic abilities to meet these demands (Gasteiger & Benz, 2018), for example, to handle counting errors productively or use appropriate mathematical language (Klibanoff et al., 2006).

At the same time, children’s mathematical development and its conditions are often not emphasised in the preparation of early childhood teachers. In some countries (including Germany), most early childhood teachers are qualified through practical training where mathematical development may not be focussed on (Blömeke, Jenßen, Grassmann, Dunekacke, & Wedekind, 2017). Even in countries where mathematical development is an obligatory subject (including Switzerland), programmes are led by colleges of education with a strong emphasis on practice. Early childhood teachers hence have few opportunities to develop CK and PCK as declarative, decontextualised knowledge.³

When using the model of professional competence (Section 1.1.) in the early childhood context, the specifics of early mathematical learning have to be considered. In this context, AC refers to the ability to recognise age-adequate mathematical affordances in play or everyday life situations and to react spontaneously and adaptively in order to support the learning processes. RC refers to the cognitive dispositions required to plan, prepare, and anticipate mathematical learning opportunities as well as to systematically use observations from play-based or everyday situations to diagnose and review individual mathematical development.

Hepberger et al. (2019) developed a measure of AC and RC for use in early childhood education, and were able to replicate the separability of the two competence components from each other and from professional knowledge. Characteristic differences found between teachers who received non-university-based professional education and those who received university-based professional education further support the validity of the interpretation of test scores (Hepberger et al., 2019).

To sum up, the presented model of professional competence and its assessment approach is suited to tackle certain difficulties in prevalent teacher knowledge research. Based on the results of initial studies, we argue that the model can be transferred to the early childhood context if characteristic features of early mathematical learning are considered.

1.3. Professional development (PD) for early childhood teachers

The characteristics of effective PD for school teachers are well described in the literature. Here, we summarise findings on organisational aspects as well as on the content structure. Most of the findings can be readily applied to the early childhood context.

With regard to the organisation of PD, Desimone (2009) showed that a longer duration leads to more effective PD: Programmes that run for a longer period of time (e.g. a six-month period) are therefore considered advantageous over more compressed PD. Moreover, Borko (2004) found that PD programmes that foster the forming of a community of practice are superior to PD programmes that neglect this aspect. If, for example, teachers from one institution participate collaboratively, the emergence of discursive practices is enhanced, which can, in turn, have a positive effect on teaching practices (Desimone, 2009). The effectiveness of PD can further be supported by PD that combines theoretical phases with coherent practical learning opportunities related to participants’ professional lives, e.g. through homework assignments (Lipowsky & Rzejak, 2015).

In addition, Desimone (2009) describes the design feature of active learning – that is, the deep interaction of the teachers with the PD topics – as being conducive to learning. Borko (2004) details that the use of records of practice is particularly suitable for supporting active learning. Situating learning opportunities with the help of approximations of practice (Grossman et al., 2009) like role-play or authentic practice samples such as classroom videos or descriptions of student difficulties can support this kind of deep interaction. Such findings led to the recommendations of case-related designs for PD. In particular, the use of video cases in teacher training was proved to be effective in various forms (e.g. Cherrington & Loveridge, 2014).

With regard to the content structure of PD, research suggests that a clear focus on content has positive effects; for example, on the mathematical competence development of children (Desimone, 2009). The development of professional knowledge, especially PCK, was also found to be an important characteristic of effective PD (Lipowsky & Rzejak, 2015). At the same time, professional knowledge is only one out of many desirable outcomes of PD. In order to change pedagogical practices, additional practical learning opportunities are required (see above, active learning), and different activities are proposed for that purpose. Again, coherence between PD content, practical learning, and everyday professional demands supports the effectiveness of PD (Borko, 2004; Desimone, 2009). According to our competence model, a distinction can be made between the everyday professional demands of teachers, that is, between the demands of planning, preparing for, or reflecting on learning situations (RC), and the demands of supporting mathematical learning processes in play or everyday life situations (AC). Activities such as the team planning of learning opportunities, the analysis and discussion of materials, or the joint diagnosis of students’ ideas can be seen as being coherent with RC requirements. Activities that are coherent with AC should aim to change pedagogical action in the situation, which could be achieved, for example, through role plays in which the desired practices are modelled and trained.

Finally, it should be noted that some desirable outcomes of PD workshops are easier to change than others. While (declarative) knowledge has been shown to be sensitive even to short PD workshops, practical actions (and beliefs) have been shown to be much more stable, and changing them requires deliberative effort (Bruns, Eichen, & Gasteiger, 2017; Lipowsky & Rzejak, 2015). For example, it has been found that adaptive practices (e.g. using students’ ideas in teaching) are more difficult to adopt than more general instructional practices (e.g. for questioning techniques; Franke, Carpenter, Levi, & Fennema, 2001).

Because research on PD is limited, it is difficult to obtain a more accurate picture of which features of PD impact which kind of outcomes. This shortfall is not least due to the fact that, so far, hardly any appropriate subject-specific measure (besides teacher knowledge tests) has been available to map the various goals of PD. Therefore, the approaches towards competence modelling may mark an important development. Although first applications have been successful, the validity evidence is still limited.

2. Research question

In this study we investigated an approach for modelling teacher competence with respect to its sensitivity to professional development, focussing on learning mathematics in early childhood education. We thus address the gap caused by the fact that there are still few comprehensively validated practice-oriented test instruments. According to the theoretical framework, the two components, action-related (AC) and reflective competence (RC), rely on different cognitive dispositions and are closely related to professional demands and professional knowledge. Hence, our research question is whether AC and RC can be differentially fostered through specific interventions. Our study aimed to find evidence that the approach to model teacher competence provides a valid structure to differentially trace teacher competence development in PD.

In line with the theoretical framework and findings from PD research, we hypothesised that two Intervention Groups (IG) participating in a PD programme with a focus on either AC or RC (IG AC, IG RC) would show differential growth of professional knowledge, AC, and RC in comparison to each other and a Control Group (CG). In detail, we expected professional knowledge to be sensitive to both interventions (but not in the control condition), AC to be sensitive only to the AC intervention, and RC to be sensitive only to the RC intervention.

3. Methods

3.1. Study design and sample

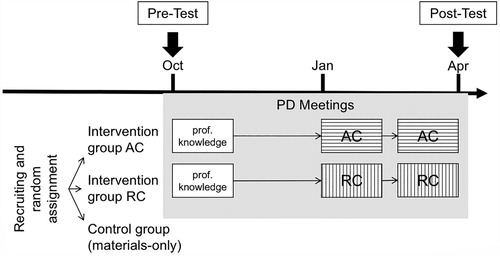
We conducted a randomised trial to investigate the hypotheses. Early childhood teachers were recruited in Germany and German-speaking Switzerland and participated on a voluntary basis. The final sample comprised N = 170 early childhood teachers (n = 87 Germany, n = 83 Switzerland), amongst them seven male teachers. The participants stated at the beginning of the project a mean of M = 13.8 years of professional experience (SD = 10.6 years), with no significant difference between the subsamples from Germany and Switzerland (t[148.82] = 1.2, p = .23). As the structure of teacher education differs in Germany and Switzerland (see footnote 3), the samples had different characteristics with respect to university-based versus non-university-based professional education. Whereas, in Switzerland, 47.7% of the teachers had a university degree, this was the case for only 7.4% of the German sample. The convenience sample cannot be regarded as representative for either German or Swiss teachers.

The participants were randomly assigned to three different conditions; two experimental Intervention Groups (IG AC, IG RC), including specific PD programmes that addressed AC and RC, respectively, and a Control Group (CG, see also Figure 2 for an overview on the study design). The random assignment was conducted on an institutional level in order to account for diffusion processes between teachers from the same kindergartens. The number of participants in the different conditions were n = 55 (IG AC), n = 60 (IG RC) and n = 55 (CG). Details of the half-year long interventions conducted simultaneously in Switzerland and Germany are given in Section 3.3.

Figure 2. Schematic overview of the study design.

All participants completed a standardised test on professional competence as a pre- and post-test. The intervention groups took the test at the first (pre-test) and the last (post-test) meeting of the PD. The control group took the pre-test at an introductory meeting (see Section 3.3. for details) and the post-test at a meeting half a year later. Due to missing data, the data set for the longitudinal analyses was reduced to N = 133 teachers (n = 67 Germany, n = 66 Switzerland, n = 42 IG AC, n = 47 IG RC, n = 44 CG). The dropout (mainly due to teachers changing institutions) ranged between 20% and 24% in all subgroups. The dropout can be considered to be random as the characteristics of the groups with and without dropout did not differ with respect to the variables available.

3.2. Instruments: professional competence and professional knowledge

We used a standardised test with partly video-based and timed items to assess professional knowledge, RC, and AC. The content of the items was aligned with the development of the numerical skills of children aged 3–6 years (Krajewski & Schneider, 2009). They model the early development with the help of three stages as the increasing ability to deal with quantity to number-word linkages: On stage 1 (basic numerical skills), abilities to discriminate between quantities and skills to deal with number words are still disintegrated. Important abilities are beginning subitising abilities and to know number words in their sequence. These abilities can be understood as precursors for quantity-number linkages which are indicative of stage 2: Children relate quantities to numbers and number words and are able to determine quantities as well as compare numbers in respect to size. On level 3, children use relations between quantities and relations between numbers in a sophisticated way, for example when (de)composing numbers. Here, we provide a short illustration of the test; a more detailed description of the development of the standardised test used in this study can be found in Hepberger et al. (2019). The same assessment approach has been used with teachers of different levels (e.g. Jeschke et al., 2019; Knievel et al., 2015).

The AC test had nine items covering the different demands of fostering students’ mathematical learning (for a sample item, see the Digital Appendix, see Supplemental data). All AC test items were video-based and administered under time pressure on a computer. For each item, one short video clip (max. 2 min) presented a realistic kindergarten situation with a mathematical learning opportunity. The teachers had to react directly to the children’s activities by talking into a headset; this should mirror the professional demands in a natural way. The RC test had nine items covering the different demands of anticipating, planning, and diagnosing children’s learning (for a sample item, see the Digital Appendix). The teachers were asked to analyse the RC situations for the purpose of planning or diagnosing and to write down their conclusions. Three of the RC items were video-based and administered on a computer, but without time pressure. The remaining RC items were paper-pencil based and in short-answer or complex multiple-choice format. The test on (basic) professional knowledge (BK⁴) with nine items covering PCK on children’s development in the area of numbers and operations was paper-pencil based and in short-answer or complex multiple-choice format.

Trained raters coded the open answers according to an elaborated coding manual (procedure aligned with Knievel et al., 2015). It provided criteria for grouping similar answers to each item according to how the answers addressed mathematical learning. The codes were then scored as 1 (full credit), 0.5 (partial credit), or 0 (no credit) depending on the degree to which they were seen to be indicative of RC or AC. Fourteen items were used as polytomous items. The remaining items were scored dichotomously (full credit and no credit). To estimate the interrater agreement, 25% of the open answers were rated by two independent raters (pre-test). The interrater reliability for this procedure was sufficient, with a mean Cohen’s kappa of M = .74 (SD = .11). Confirmatory factor analyses confirmed that the test used in this study was suited to discriminate between AC, RC, and professional knowledge (Hepberger et al., 2019).

3.3. Experimental conditions: professional development programmes of the intervention groups and the materials-only control group

Two highly-specified intervention-group conditions (with a focus on AC or RC) and a control-group condition were designed for this study (see Figure 2 for an overview on the study design). The interventions were designed as PD with a focus on children’s abilities in the area of numbers and operations and they lasted six months (end of October – mid-April). The PD used board games, as they have been described as providing effective learning opportunities (Gasteiger, Obersteiner, & Reiss, 2015; Young-Loveridge, 2004). Participants received a box with 10 board games (selected and adapted from Hauser, Rathgeb-Schnierer, Stebler, & Vogt, 2015)⁵ at the first meeting in October (150 min PD time, not including breaks). The intervention groups met again twice between January and mid-April for two further PD sessions (each 150 min PD time). Teachers were asked to play the games twice a week for 30 min with 4–5 of the kindergarten children they care for.

The PD sessions provided prolonged, material-based training that was connected to professional practice through approximations (Grossman et al., 2009). The PD sessions also comprised further characteristics of effective teacher training (see Section 1.3). The PD sessions for both intervention groups started with an introduction to the games (60 min) to make the teachers familiar with them. In addition, the participants received a brief theoretical input (60 min) addressing aspects of professional knowledge related to the development of young children’s understanding of numbers and operations according to the model of Krajewski and Schneider (2009). We used short videos to illustrate the main steps of children’s numerical development and, hence, provided a case-related design. The introductory sessions did not differ between the AC and RC interventions.

Starting with the second PD session, the interventions followed different rationales and focused on learning opportunities for either AC or RC, according to the state of research in early mathematics as reported in Section 1.2. This was achieved through case-based activities as approximations of practice (Grossman et al., 2009) that, in line with the theoretical differentiation, represented either the demands of planning, preparing for, or reflecting on mathematical learning opportunities (RC) or the demands of supporting mathematical learning processes during instruction (AC). The interventions are portrayed in more detail in the next paragraph. Despite the different competences targeted and the different focus of the activities, the interventions were still closely aligned with respect to the design: They both comprised a combination of theoretical input phases, work with video cases, and homework related to the game sessions with the children. Therefore, the PD sessions were closely connected to the practical work. The PD sessions were further organised into regional groups in both Germany and Switzerland, each with a maximum of 18 participants. Teachers from one institution joined the same sessions. Thus, the recommendations for how PD programmes can effectively foster communities of practice were met.

In detail, the RC intervention addressed the diagnosis of children’s developmental level with respect to numbers and operations. Additionally, the intervention dealt with the planning of learning opportunities through analysing board games with respect to their potential to foster mathematical development. Activities included the (collaborative) diagnosis of video cases that showed children at a critical developmental stage playing the board games. Teachers further played selected games themselves and discussed their potential for learning in small groups. They discussed possible variations of the games (e.g. exchanging regular dice with dice with number symbols) and their impact on the potential for learning. The sessions included activities to select games according to diagnoses and to give reasons for the decisions made. The homework tasks required the teachers to observe and diagnose the abilities of the children in their group during the game sessions and to plan, implement, and document mathematical learning opportunities accordingly. Homework assignments were not systematically collected due to data privacy issues but they served as a private means for the teachers to monitor their own learning process.

In contrast to the RC intervention with its focus on planning and reflecting on learning opportunities, the AC intervention addressed how teachers can provide high-quality learning support during the game sessions (scaffolding) and focused on specific strategies (e.g. use of “math talk”, questioning, use of errors or misconceptions, structuring of solution processes, use of representations). Strategies were modelled partly via video cases or role play. Teachers had, for example, to come up with different possible domain-specific teacher actions for situations presented in a video. The teachers further played the games in role plays, with one teacher practicing different strategies while the other teachers in the group played the children at a specific level of mathematical development. The homework tasks in the AC intervention group asked the teacher to observe, describe, and document their own actions during the games with a focus on different strategies and to find potential ways of improving their practices. For the same reason as given above, homework assignments were not systematically collected.

All interventions were highly specified and carried out by trained project staff (Authors 2–5). All facilitators were acquainted with the aims and rationale of both interventions and were trained not to address specific aspects of the contrasting intervention in order to maintain the different focus of the interventions. For example, the RC intervention did not address how teachers should interact with children during games. In the same way, diagnosing children’s skills and selecting games according to the diagnosis was not explicitly addressed during the AC intervention.

The control group also met for an introductory session and received the box of games and an introduction to the games (60 min). In contrast to the intervention groups, the control group did not receive any input on professional knowledge related to the development of young children’s understanding of numbers and operations. Instead, the teachers crafted some materials for the games themselves and played the boards games more extensively. The control group can be described as a materials-only intervention. The teachers were – similar to the intervention groups – asked to implement the board games over six months in order to gain practical experience. At the end of the study, the control group met primarily for the purpose of taking the post-test.⁶ The control group can accordingly be considered a strong control group with a potential impact on teacher competence through practical work.

3.4. Data analysis plan

The analyses in this study used Item Response Theory (IRT) models, namely one-dimensional Rasch models (1PL) with partial scores. The IRT considers that even teachers with low competence can sometimes solve a difficult item and teachers with low competence can sometimes fail on an easy item. The person’s abilities are estimated as Weighted Likelihood Estimators (WLEs) according to Warm (1989). Following the competence model, scales were estimated for AC, RC, and BK. As the theoretical base and prior empirical findings suggest a close interrelation between RC and BK, we also considered a further scale: RCBK (mirroring slow demands).

These Rasch models map item difficulties and individual abilities (person parameters) on the same scale. To compare person abilities across time, the application of a linking method to connect the pre- to the post-test was necessary. We first estimated item parameters based on the post-test data (141 observations) for each scale, with person parameter means fixed to zero. Subsequently, we fitted Rasch models to the complete data (302 observations) with item parameters fixed.

Item fit was evaluated with the help of fit indicators. We applied a moderate criterion of 0.75–1.33 (according to Wilson, 2005) to evaluate outfit and infit MNSQ. In order to investigate the psychometric quality of the instrument for longitudinal measurement, we inspected the WLE separation reliability of the scales, which indicates how efficiently the test can separate persons of different abilities. Person separability hence impacts the possible detection of longitudinal effects. It is an indicator comparable to Cronbach’s alpha and can be interpreted in the same way (Clauser & Linacre, 1999). Values bigger than .8 are usually considered good and values bigger than .7 acceptable, but some authors question the rigid use of a cut-off value for these indicators, as they depend on scale length and the homogeneity of the items (Cortina, 1993). For certain uses, for example, if complex ability constructs are measured with inhomogeneous item types and a restricted number of items, values as low as .6 are considered acceptable (Cortina, 1993) although the detection of longitudinal effects might be hampered by such low reliabilities.

The analysis of the intervention effects on AC, RC, and BK and a combined RCBK measure were investigated with four separate linear mixed models. As fixed factors, we entered the interaction term time × group into the models. As random effect, we inserted intercepts for subjects. The analyses are comparable to two-way split-plot-factorial Analyses of Variance (ANOVA). Visual inspection of the residual plots did not reveal any obvious deviations from homoscedasticity or normality. P-values were obtained by likelihood ratio tests of the full models with the intervention effect against the models without the effect in question. Potential differences between the pre-tests of the different groups were investigated with models using only the group as a fixed factor; this is equivalent to one-way ANOVAs. Post-hoc analyses (Tukey) conducted on the basis of the estimated marginal means were used to explain the effects.

All analyses were computed with the software R (version 3.3.2). IRT analyses were conducted with the library TAM (version 2.8, Robitzsch, Kiefer, & Wu, 2017), linear mixed models with the library lme4 (version 1.1, Bates, Mächler, Bolker, & Walker, 2015). Estimated marginal means and contrasts were evaluated with the library emmeans (version 1.3.3, Lenth, 2019).

4. Results

4.1. IRT scaling

The item out- and infits of the 16 (AC and RC), 10 (BK), and 26 (RCBK) item parameter estimates⁷ were investigated for the three scales AC, RC, and BK. Most parameters fell within the criterion range. Only one item parameter from BK was affected by an underfit of item outfit and one item parameter of AC by an underfit of item out- and infit. As underfits are considered unproductive for the construction of measurement, but not degrading (Wright & Linacre, 1994), we decided to keep both items.

The WLE reliability of the resulting scales ranged from .57 to .69. The AC scale and the combined RCBK scale showed reliabilities close to .70 (acceptable) and can hence be considered suitable for detecting longitudinal effects. The scales for RC and BK, with WLE reliabilities just below .60, are less suited to detect longitudinal effects.

The manifest correlations between the scales were significant, and mostly of moderate size with the correlation between AC and BK being just below .30 (r_AC-RC = .37, r_AC-BK = .29, r_RC-BK = .36, r_AC-RCBK = .42, all p < .001). The pattern of correlations hence is comparable to findings from other studies (e.g. Knievel et al., 2015); RC was – in line with the theoretical considerations – related to BK more strongly than AC.

4.2. Differential effects of the intervention

The sensitivity of the different components of teachers’ competence with respect to the conditions was investigated with linear mixed models. Our dependent variables were the person parameter estimates of the respective scale. Table 1 lists the means and standard deviations for the whole sample. The values are presented in logits (WLEs, means for post-test centred to zero) and can theoretically range from −∞ to +∞. Due to the IRT scaling procedures, differences within a scale across the different points of measurement are meaningful.

Table 1. Descriptives for pre- and post-test scores, tests of difference, and effect sizes.

	Pre-Test Score			Post-Test Score			T-Test of difference (df = 132)	Effect size
	M(SD)	Min	Max	M(SD)	Min	Max	t-value (p)	d
AC	−0.31(1.08)	−3.07	2.64	0.01(1.16)	−4.39	3.86	3.386***	0.29
RC	−0.43(0.89)	−4.82	3.48	0.00(0.92)	−2.27	3.48	5.789***	0.50
BK	−0.51(0.74)	−2.66	1.29	0.00(0.85)	−1.78	2.73	6.108***	0.53
combined RCBK	−0.72(1.26)	−5.03	3.15	−0.02(1.28)	−3.33	3.15	8.052***	0.70

Note: ***p < .001, **p < .01, *p < .05.

We first investigated potential differences between the groups (IG AC, IG RC, CG) with respect to pre-test scores by conducting ANOVAs. Despite the random assignment to groups, a significant difference was found in the pre-test scores for AC (F[2,130] = 4.347, p = .01). Pairwise post-hoc comparisons (Tukey) indicated that the estimated mean score for the IG RC (M = −0.57, SE = 0.15) was significantly lower than for the IG AC and the CG (IG AC: M = −0.29, SE = 0.16, CG: M = .06, SE = 0.15), which themselves did not significantly differ from each other. No difference was found between groups with respect to pre-test scores of RC and BK and the combined RCBK (RC: F[2,130] = 1.078, p = .34, BK: F[2,130] = 0.591, p = .56, RCBK: F[2,130] = 0.680, p = .51).

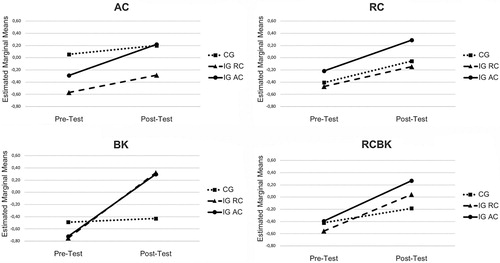
The mean scores on all scales were significantly higher in the post-test than in the pre-test, with medium effect sizes found for all scales except AC (small effect), as t-tests revealed (see Table 1 for complete descriptives). On average, participants showed gains in all measures, although not necessarily on the individual level, as indicated by the drop in minimum test scores for AC between pre- and post-test. Hence, we expected a main effect of time. We modelled the fixed categorical factors of time (pre-/post-test) and group (IG AC, IG RC, CG), as well as the interaction between the factors (time × group) in separate models for each component. We compared these full models against null models using only the time factor.

The full linear mixed models indicated a better fit than the null models for all scales except RC (AC: χ²[4] = 10.859, p = .03, RC: χ²[4] = 5.986, p = .20, BC: χ²[4] = 18.379, p = .001, RCBK: χ²[4] = 12.369, p = .01). Table 2 summarises the results for the full models (reference: CG at pre-test). We have highlighted the cells where we expected to find significant parameter estimates according to our hypotheses. For AC, the main effect of time vanished after the group factor was inserted. The significant parameter estimate of IG RC partly reflects the differences in the AC pre-test, where participants of the IG RC scored lower than the other participants. The interaction effect of the time × group factor did not reach significance. For RC, in accordance with the model comparisons where the full linear mixed model failed to show a better fit than the null model, the main effect of time dominated potential other effects so that the gains of the groups did not differ from each other. For BK, the main effect of time vanished in the full model and an interaction effect of the time × group factor was detected without a main effect of the group factor. The additional analysis for the combined RCBK scale indicated a main effect of time (cf. RC results) and an interaction effect of time × group as well.

Table 2. Parameter estimates for the full linear mixed models, reference: control group at pre-test, shaded cells indicate where we expected to find effects according to our hypotheses.

Model	AC			RC			BK			RCBK
Predictors	Esti­mates	SE	p	Esti­mates	SE	p	Esti­mates	SE	p	Esti­mates	SE	p
(intercepts)	0.06	0.16	.74	−0.42**	0.13	<.01	−0.49**	0.18	<.01	−0.42***	0.12	<.001
post-test	0.14	0.16	.36	0.35**	0.12	<.01	0.06	0.19	.76	0.24*	0.10	.02
IG RC	−0.63*	0.23	.01	−0.07	0.18	.72	−0.26	0.25	.31	−0.14	0.16	.40
IG AC	−0.34	0.23	.14	0.19	0.19	.32	−0.23	0.26	.37	0.03	0.17	.86
post:IG RC	0.14	0.22	.53	−0.02	0.16	.88	1.01***	0.27	<.001	0.36*	0.15	.01
post:IG AC	0.36	0.23	.11	0.16	0.17	.36	0.96***	0.28	<.001	0.42**	0.15	<.01

Note: ***p < .001, **p < .01, *p < .05.

Post-hoc contrasts of the estimated marginal means showed that the IG AC was the only group with significant growth in AC (ΔM = 0.51, SE = 0.16, t[130] = 3.14, p = .02, d = 0.27). With respect to BK, both intervention groups showed gains from the pre- to the post-test (IG AC: ΔM = 1.02, SE = 0.20, t[130] = 5.13, p < .001, d = 0.45; IG RC: ΔM = 1.07, SE = 0.19, t[130] = 5.71, p < .001, d = 0.50) whereas the control group did not show any significant growth, with almost identical estimated means for the pre- and post-test (ΔM = 0.05, SE = 0.19, t[130] = 0.31, p = 1.0). Figure 3 summarises the effects graphically.

Figure 3. Graphical display of the estimated marginal means according to the full linear mixed models.

5. Summary and discussion

We designed two closely aligned interventions with a focus on AC and RC for early childhood teachers in order to investigate whether these two components of teacher competence can be differentially fostered through specific interventions. The findings of our controlled experimental study in the context of early childhood education are partly in line with our hypotheses. As expected, the measure of professional knowledge was similarly sensitive to both the AC and RC interventions, whereas teachers of the materials-only control group did not develop their professional knowledge. Our results indicate that the AC intervention group was the only group with a growth in AC, although the time × group interaction did not reach significance, which seems to be an effect of the sample size. With respect to the RC measure, our hypotheses were not met. All groups, intervention groups as well as control group, gained in RC in our study so that we could not detect any differential growth for this competence component.

To the best of our knowledge, this is the first study to provide evidence that a teacher competence model can be used to trace the differential effects of professional development (Desimone, 2009). In sum, we were able to show that the professional knowledge, RC, and AC of teachers is sensitive to PD and that different PD interventions (and a control group) lead to different change profiles. This contributes to the evidence on the structural validity of the approach used (AERA, APA, & NCME, 2014).

It is well known that planning and scaffolding children’s mathematical learning in the early years is challenging, since mathematical learning opportunities are often associated with play or everyday situations and are often not clearly marked as learning opportunities. It should therefore be emphasised that this study succeeded in tracing a development of competences with the help of the presented model of professional competence and its assessment approach.

However, not all fine-grained hypotheses on differential sensitivity of these measures were met and our study has some limitations. First, the convenience sample cannot be regarded as representative for German or Swiss kindergarten teachers, and despite a random assignment to groups, the pre-test scores partly differed between groups. In detail, teachers in the RC intervention group started with the lowest scores on all measures and the difference in AC reached the level of significance. The poor starting conditions of this group (IG RC) may have partially hampered our aim of tracing a differential impact of the RC intervention. Second, the sample size was small, the number of items per scale was small, and our study could be considered to be slightly underpowered. The reliabilities of the scales of RC and BK were only marginally acceptable for longitudinal analyses. This potentially weakened the power to detect differences in competence. Third, during the AC intervention, we observed that it might have provided (unforeseen) learning opportunities for RC. The design of the AC intervention group focused on specific strategies to provide high-quality learning support during games and we used role plays during the intervention. So, the interventions followed recommendations on effective PD (see Section 1.3). But trying to enact a child with specific abilities might have – as a by-product – improved the teachers’ abilities to diagnose children’s abilities or to prepare apt learning opportunities. It might also have stimulated the teachers to revisit the newly developed professional knowledge through deliberate problem-solving processes, which, in turn, could be an opportunity to learn for RC, according to the dual cognition theory. As teachers took turns in enacting children, this might partly explain why teachers in the AC intervention group also developed RC, although facilitators were trained to avoid a blurring of the interventions. Finally, we do not have data about the implementation frequency of the games, which means that the possibility cannot be excluded that the teachers’ practical learning opportunities varied.

Despite these limitations, two observations in our study are especially interesting from the perspective of validating the internal structure of the theoretical framework. First, despite a similar growth in professional knowledge (BK), the RC intervention group could not keep pace with the AC intervention group’s growth in AC. This adds evidence to the distinctness of AC and professional knowledge as well as RC, as assumed by the dual cognition theory in our framework (see Section 1.1). Looking at the profiles of gains, we observed that the control group developed RC without noteworthy changes in BK. This adds evidence to the distinctness of RC and professional knowledge, as assumed. The control group was designed as a materials-only control group, so the RC findings might indicate that a certain competence (related to the preparation of and reflection on mathematical learning situations) can be developed through practical experience when using the materials, possibly embedded in collaborative practice (Borko, 2004), and even without an adequate professional knowledge base. However, as we lack information about whether teachers might have learnt from participating in our assessment, we cannot exclude an alternative explanation of the RC findings through retest effects.

Second, our study replicated previous findings on PD (see Section 1.3): The interventions focused on professional knowledge as recommended by PD research and clearly affected the development of professional knowledge, as shown by the medium effects found. The AC intervention group showed gains with only small effects, which resonates with the previous findings from Franke et al. (2001) that adaptive practices are difficult to change. We cannot conclusively derive a statement about the conditions of the trainability of RC.

The model of teacher competence with its close relation to professional demands was specifically developed to capture professional growth of teachers from a broader, situated perspective, and previous work from different contexts has made the approach appear promising. The study presented in this paper presents first evidence that teacher competence is partly differentially sensitive to specific PD. Teacher competence models may therefore indeed be suitable for differentially tracing teacher growth towards higher expertise.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was jointly funded by the DFG–German Research Foundation under the grant numbers LI 2616/1-1, HE 4561/8-1, LE 3327/2-1 (DFG) and the SNF–SwissNational Science Foundation under the grant number 100019L-156680 (SNF).

Notes

1 There are alternatives to the dispositional view of competences (e.g. McMullan et al., 2003) considering competences, for example, as performance or general skills. In this article we take the dispositional view.

2 We use these terms as presented in the dual processing literature, although they might lead to a simplistic view that overemphasises the time factor over other resource restraining factors.

3 Early education teachers in Germany are usually educated in full- or part-time professional schools (Fachschulen, Fachakademien) located at tertiary level, although university-based professional education is also becoming increasingly common. Early education teachers in Switzerland are today educated at universities of education since non-university-based education ceased in 2001. Accordingly, the more experienced teachers mostly graduated from non-university-based schools. Please see Oberhuemer, Schreyer, and Neuman (2010) or the Eurydice descriptions of the national education systems, chapter 9, at https://eacea.ec.europa.eu/national-policies/eurydice/national-description_en for details.

4 We use the abbreviation BK for the professional knowledge test in order to avoid confusion with the acronym PK, which is used for Pedagogical Knowledge, a non-subject-specific professional knowledge component. BK hence references to the role of content-specific professional knowledge as the basis of professional competence.

5 The board games were partly conventional games such as shut the box (with modified rules) and partly games designed for mathematical learning in early childhood. English descriptions of sample games are provided in Stebler et al. (2013) and Vogt, Hauser, Stebler, Rechsteiner, and Urech (2018).

6 Due to ethical reasons, the control group was offered an additional PD meeting on a voluntary base after data collection for this study was completed.

7 Please note that, due to partly polytomous scoring, the number of item parameters differs from the number of items.