Digital teaching platforms: the use of dynamic functions to express mathematical content

ABSTRACT

This article explores how seven Swedish digital teaching platforms in mathematics make use of the affordances provided by various modalities and dynamic functions. A model based on social semiotics is used to analyse how dynamic functions are used, whether or not the language is technically oriented, if relational or operational processes are emphasised, and the logic in the text. The analysis focuses on how the dynamic elements in teaching materials are used and potential consequences of their use. The results reveal a tendency to predominantly allocate dynamic and interactive elements to tasks related to theoretical parts and examples, and also that the most common dynamic element, film, has substantial potential to support meaning-making in several respects. For example, a voice-over can easily contribute a personal touch, add further logic to the content, or give an explanation based on an operational process.

KEYWORDS:

• Film
• digital teaching material
• social semiotics
• multimodality
• drag-and-drop

In recent years, there has been very strong digital development within schools (OECD, 2021), and the use of digital teaching materials has increased. According to the TIMSS 2019 report (Trends in International Mathematics and Science Study), 37 per cent of grade eight students worldwide had access to computers during mathematics lessons, even though the access varies between countries, with Australia, New Zealand and the Scandinavian countries at the top (Mullis et al., 2019). Compared to print materials, digital teaching materials can take advantage of dynamic functions and various modalities such as sound, movies and animations to support students’ meaning-making. Despite all the benefits of digital teaching materials, digitisation in mathematics teaching is not solely a success story, as indicated, for example, by the 2015 PISA survey showing that across OECD countries, students who do not use computers in their mathematics lessons tend to perform better in the subject than those who do (OECD, 2015). Previous studies (e.g., Byun & Joung, 2018) point to the importance of carefully designed teaching materials that express mathematics in a well-thought-out way, so that the quality of the teaching materials is not traded away for the sake of digital functions. The aim of the present study is to contribute a deepened understanding of how digital teaching platforms in mathematics make use of the affordances provided by various modalities and dynamic functions. We also discuss how different design choices and affordances in the dynamic medium that are not fully utilised can potentially affect what meanings are offered to the reader. The Swedish case serves as a contemporary example.

Digital resources as means to support learning

Many kinds of digital teaching materials and digital learning resources are used in mathematics teaching. For example, Pepin et al. (2017) describe the difference between research on digital curriculum resources and research on digital technology, and Usiskin (2018) describes the development towards exclusively electronic teaching platforms with rich opportunities to include interactive elements. Digital teaching platforms provide opportunities to present content through several different modalities (e.g., text, images, videos, tables and figures) while also offering interactive activities. A better understanding of such advantages is important in the teaching and learning of mathematics. Students’ perceptions about mathematics can affect how the material is used, and the teacher might need to encourage students to invest enough time to grasp the content. Students with an instrumental view of mathematics are prone to using digital functions merely as tools for calculation or to check solutions, whereas those who view mathematics as a coherent system of knowledge use digital functions to make sense of course material and develop their understanding of the topic (Zeynivandnezhad et al., 2020). Students who lack any clear view of the purpose of mathematics teaching may just rush to get the correct answer, instead of striving for understanding and learning. Therefore, when digital teaching materials offer many tasks with short answers, there is a risk of unconsidered trial-and-error behaviour and skimming through tasks (Bartelet et al., 2016). A deepened knowledge about which affordances of digital teaching material encourage sense-making is therefore valuable.

Digital teaching platforms and the utilisation of dynamic features

Pepin et al. (2017) describe that it is common to use videos and animations in digital teaching materials when new areas are to be introduced, in order to increase the students’ interest. The subsequent parts of the teaching materials, with tasks and exercises, often follow a rather traditional approach, with a focus on methods and mastering of procedures. Highly dynamic functions such as “drag-and-drop exercises” can be used, for example, to show geometrical properties, with the student dragging an object on the screen. Geometrical properties can thus be perceived both visually and kinaesthetically, which can serve as support for learning. The advantage of such materials can be established based on results where students with lower achievement levels in mathematics who were used to working with GeoGebra achieved better results than high-performing students who were not accustomed to working with GeoGebra (Baccaglini-Frank, 2021). When digital teaching materials are contrasted with print material, it is found that that dynamic features distinguish the digital environment, but the option to manipulate can to some extent be obtained by using physical manipulatives. A study by Lee and Chen (2016) comparing the teaching of fractions with dynamic digital materials with teaching the same content with physical manipulatives revealed no significant differences in learning. Digital materials can however support visualisation of relations between objects and between concepts in ways that are not possible with physical objects. The affordances of digital media have been shown to be particularly beneficial in tasks where students are given the opportunity to manipulate several representations in non-routine tasks. Students learning under these circumstances outperform those learning similar content in routine tasks with digital materials or physical objects (Lee & Chen, 2016). Clearly, there are affordances in the digital environment, but there are also affordances of print material and of physical manipulatives, and a deepened knowledge about what is unique for the digital media brings with it an understanding of when other materials are to be preferred.

One prominent unique feature of digital media is the option to use digital manipulatives that can represent mathematical objects. A meta-analysis of 66 research reports about the effects of digital manipulatives on students’ achievement reveals convincing affordances of these materials. For example, the materials encourage creativity, increase the variety of students’ solutions, encourage simultaneous linking of representations and motivate students to persist in problem solving (Moyer-Packenham & Westenskow, 2013). The possibility to dynamically link representations is a prominent affordance of digital materials, because it supports the development of a relational understanding of mathematics. Students can experience such relations by, for example, dragging objects in a graph or relating strip diagrams to fractions expressed with symbols, and receiving feedback from the material. Previous research on digital teaching platforms in mathematics does however indicate that dynamic elements used in the theory parts and in examples often turned out to have a slightly lower degree of interactivity than in tasks (Dyrvold, 2022). In parts presenting theory or examples, boxes with hints or a voice-reading function were common, whereas more interactive resources, such as activities where the students are expected to manipulate materials, were rare. The tasks, on the other hand, often contained dynamic functions with a higher degree of interactivity. These could, for example, involve various forms of dynamic feedback, such as elements that respond to actions taken by the student.

Apart from new modalities that can be utilised in digital teaching platforms, the option to provide different kinds of feedback is prominent, something that has been highlighted as an asset of digital teaching materials (Leung & Baccaglini-Frank, 2017). Tasks with a multiple-choice design, as well as tasks demanding constructed responses, are commonly used in digital teaching platforms (Dyrvold, 2022). It is a more cognitively demanding task to construct an answer yourself than to choose a pre-formulated one (Glynn, 2012). Having the opportunity to construct the answer can induce students to evaluate, integrate, and elaborate on their understanding, demands that are beneficial for learning. The feedback on answers to such tasks also differs in usefulness depending on type. The effect size on learning outcomes is much larger for detailed feedback than for feedback regarding correctness or information about the correct answer (Van der Kleij et al., 2015). Dynamic feedback provided in relation to tasks (in mathematics and other subjects) has proven beneficial for learning, and a review contrasting human tutoring and multistep intelligent tutoring systems reveals that digital feedback during problem solving is nearly as effective as human tutoring, with an effect size of .76 (Van Lehn, 2011). The digital medium is an asset here, because feedback automatically adapted to a particular reader is not possible to offer in print. A study evaluating the usefulness of different digital learning models found that training adapted to students’ scores on a pre-test was significantly more effective for improvement of misconceptions and for learning achievement than training where no individual adaptation was made, especially for students with a low-level of prior knowledge (Wang, 2014). In Wang’s study the adaptation was based on a pre-test, but digital media also provide large opportunities to give different kinds of feedback depending on the reader’s actions.

In conclusion, there are many reasons to expect learning gains when digital teaching platforms are used, but there is also potential for developing these materials, and it can be problematic to draw far-reaching conclusions about the advantages of digital teaching platforms. For example, Byun and Joung (2018) showed that the use of learning games in mathematics teaching often leads to positive effects on learning, but the learning fostered by these games is often limited to basic knowledge and has limited possibilities to support student learning on a higher level. Thus, it is important to review what mathematical content is offered, or not offered, in learning games and in all teaching materials, digital as well as printed. In addition, there are affordances of print media that are lost in their digital counterparts. Usiskin (2016) discusses challenges that arise when paper textbooks are moved to digital platforms, and suggests that the optimal solution may be a combination of the two media. For example, the space available in paper textbooks makes them preferable for large schematic overviews, whereas digital media can show dynamic change. A recent study about the use of different versions of teaching materials reveals a tendency to keep the printed version as a complement when using a digital textbook. In a comparison of 78 classrooms, 40 per cent of those with a digital version (e-textbook or digital with interactive components) also had access to a print version. Of 67 student teachers in the study, 36 per cent ranked a printed textbook as their first choice to have their students use (Gay et al., 2020). These studies suggest that digital teaching materials may be used for particular purposes, whereas the print version serves other purposes. In order to fully exploit the advantages of digital learning materials, both designers and users of these materials need in-depth understanding of how they can be used and what advantages and disadvantages they entail.

Theoretical perspective

To investigate form and function in multimodal and dynamic digital teaching platforms, this study builds on social semiotic theory (see e.g., O’Halloran, 2005; Kress & Van Leeuwen, 2021) and an analysis model developed for analyses of digital teaching materials in mathematics (Bergvall & Dyrvold, 2021). A cornerstone of social semiotics is that all instances of communication are made up of three metafunctions: an ideational function, which means that the communication expresses some kind of content or idea; an interpersonal function, because some form of relationship is always created between the participants in the communication; and finally a textual function, which is about how the communication is structured and arranged to connect the content and the different parts of the communication, and thus to create a flow of information. The analysis model (Bergvall & Dyrvold, 2021) is intended for analysis of digital teaching materials in mathematics. An analysis based on this model can provide an in-depth description of the expressed mathematical content. In particular, there is an emphasis on the role of design choices for the offered meaning when it comes to relational and operational processes, interpersonal aspects (coding orientation), and how the logic of mathematics is expressed and exhibited using dynamic functions. The following sections describe how the analysed aspects are of relevance for mathematics education and give reasons for our decision to include these aspects in the analysis.

Operational and relational processes in mathematics

Within social semiotics, processes are described as part of the ideational metafunction. Processes indicate, for example, that something happens, is performed, said or exists. Several different process types can be expressed in natural language, but when it comes to visual representations, they are mainly divided into narrative and conceptual processes (Kress & Van Leeuwen, 2021). These are here understood as equivalent to operational and relational processes, which in research on mathematics education are often described as important components of mathematical knowledge (e.g., Hiebert, 1986; Sfard, 1991; Morgan, 1998; Alshwaikh, 2011). A part of a mathematics text is defined as expressing an operational process if it concerns something that is supposed to be done, for example a calculation. A part of a text that expresses relations between mathematical objects, on the other hand, is defined as expressing a relational process.

Several previous empirical studies have focused on the development of operational and relational knowledge (e.g., Rittle-Johnson et al., 2001, 2015) and come to the common conclusion that mathematical competence depends on developing both conceptual and procedural knowledge, and the relationship between these is bidirectional. Developing procedural knowledge supports the development of conceptual knowledge and vice versa. This can be related to Sfard’s (1991) description of conceptual understanding as a synthesis of operational and relational understanding through reification. Operational and relational understanding thus both play an important part in understanding a concept. How the object-process relationship is expressed in mathematics teaching is important, and this aspect is included in our analysis model in order to shed light on if and how operational and relational modes of understanding are offered to the student via dynamic functions.

How mathematics is expressed as naturalistic or technically oriented

One analytical layer in the model concerns coding orientation and touches on the type of truth claims expressed in a text (Kress & van Leeuwen, 2021). For example, if the purpose of a text is to present an everyday context as a realistic example with high credibility, this is expressed by the use of naturalistic images, references to places, concrete objects and personal references. If, on the other hand, the text expresses a strictly mathematical situation with high intra-mathematical credibility, mathematical notation and schematic images are expected, because diagrams, graphs and tables can be assumed to give high credibility and to make strong truth claims within mathematics. Coding orientation can be linked to research in mathematics education about how the student is positioned in relation to mathematics, and what types of mathematical activities the student is invited to participate in. Human agents, connections to real-life situations and pictorial images express mathematics as a human activity, something that exists in students’ everyday life and that they are invited to interact with. A high frequency of technical and subject-specific expressions, on the other hand, indicates a description of mathematics that is “alienated” (Morgan & Sfard, 2016).

There are many studies in mathematics education research that relate in some way to coding orientation, even if they use other theoretical and conceptual frameworks (e.g., Harvey & Averill, 2012; Riggs et al., 2017; Stylianides & Stylianides, 2008). These studies concern issues such as the importance of how mathematics is presented, whether truth claims are based on a naturalistic understanding of mathematics connected with everyday life where the student is invited to act, or if mathematics is depicted as distant from the student’s everyday life with a coding orientation using intra-mathematical truth claims. Results reveal that a real-life context can both support learning (Harvey & Averill, 2012) and entail challenges (Riggs et al., 2017; Stylianides & Stylianides, 2008). The present study includes coding orientation as an analytical layer in order to investigate how the relationship between humans and mathematics is expressed by means of dynamic functions.

How logic is expressed in digital mathematics teaching platforms

In addition to coding orientation and processes, this study concerns how a mathematical concept is logically presented to the students through logical networks connecting and highlighting different central aspects of the concept. These logical networks are investigated through expansions. The theoretical understanding of expansions has been developed from the work of Van Leeuwen (2005) and has previously been described by Bergvall and Dyrvold (2021). In expansions, new key aspects of concepts are introduced or previously presented aspects are described in a new context. Logic is an essential part of mathematics, and analyses of the relation between the difficulty level and textual features of tasks have revealed that tasks with many meaning relations between concrete and abstract objects have high mathematical difficulty but do not impose high reading demands (Dyrvold, 2020), which indicates that meaning relations are important to take into account in analysing mathematical texts. In the present study, particular attention is given to how logic is expressed in digital teaching platforms, and we investigate meaning relations in the form of different types of expansions and what roles the different dynamic functions have in the expansions of the concept of proportionality.

Method

Data

The empirical data in this study consists of seven Swedish digital teaching platforms in mathematics intended for lower secondary school (TP1 - 7). The selection criteria were that they had all their educational material fully integrated in the digital environment and covered the entire syllabus. To enable a qualitative analysis of seven different sets of teaching material, the data had to be limited to one mathematical area, and proportionality was selected. This content area was chosen because it provides plentiful opportunities to use and combine different types of semiotic resources and dynamic functions. For example, geometry was assumed to be expressed by visual resources to a great extent, while mathematical notation was assumed to predominate in algebra. If different content areas had been studied in the different platforms, we would risk missing opportunities offered by the combination of different semiotic resources. A section about proportionality was chosen from each teaching platform, and three parts of each of these sections were included in the analysis: the theoretical part where proportionality is introduced; an example showing how to solve a task with proportionality; and as many tasks as were needed to capture all the dynamic functions present in each teaching platform. These three parts (theory, examples, and tasks) were present in all the analysed platforms. The aim of this study was not to compare the different teaching platforms, but rather to investigate how affordances provided by various modalities and dynamic functions are used in digital teaching platforms in mathematics, which is why the smallest number of tasks needed to include all the dynamic functions were analysed.

Analysis

Guided by the aim of the study an analysis process consisting of four steps was developed. This process is first presented. Thereafter the analytical layers used in the second step of the analysis are presented more in detail.

Analysis in four steps. In the first step, the parts from each teaching platform (theory, examples, and tasks) were divided into elements. An element can, for example, be a coherent piece of text, an image, or a solution to a mathematical task described with words and mathematical notation. Elements were distinguished and regarded as separate if there was distance between them in the layout or in terms of content. In the second step, each element was coded in relation to the four functional layers (base layer, relational layer, process layer, and logical layer) based on the social semiotic model of analysis of teaching materials in mathematics described by Bergvall and Dyrvold (2021). In the third step, the coding from step two was compiled for each layer in each teaching platform. In the compilation, patterns were sought in relation to the theory. The purpose was not solely to describe the most common features, but also to highlight more unusual ways of using digital resources, in order to capture the breadth of the materials. The compilation was made with the analysed teaching platforms at hand. In the fourth step, the results from the different teaching platforms were merged together to identify and describe various characteristics of digital functions in teaching platforms in mathematics. Summaries were made, and examples that well represent various functions of the materials were chosen for presentation. In the following paragraphs, the four layers that were taken into consideration in the second analytical step are presented.

Analysis in four analytical layers. In the analysis of the base layer, each element was categorised according to its semiotic resource (natural language, image, or mathematical notation) and modality (visual or audible). All dynamic functions in the text were also identified and described, as well as how these dynamic functions invite interaction. For example, a film is very dynamic because it changes continually, but it does not invite interaction, whereas multiple-choice questions are only instantaneously dynamic but demand interaction.

In the analysis of the relational layer, the analysis focused on coding orientation, that is, whether the emphasis is on an everyday context (naturalistic coding orientation) or on stringency and technicality (technical coding orientation). All elements in all analysed teaching platforms were coded as having a naturalistic or a technical coding orientation, or both. The coding mirrors the sense in which the mathematics is offered to the reader – as something closely related to everyday human life or as something distanced and alienated. The coding is based on all semiotic resources used in an element, but an overall assessment was made of what resources were especially pronounced because, for example, mathematical notation is technical per se, and it is not meaningful to code each element with mathematical notation with a technical coding orientation. A paragraph describing an everyday context that includes “km/h” is accordingly coded as naturalistic despite the units. Elements including both types of constituents are coded as naturalistic and technical; an example would be a paragraph with one sentence referring to everyday life and another that is densely packed with technical terms and notations.

The analysis of the process layer concerns whether mathematics is offered as a system of relations or as something in which the reader is invited to actively take part. There is a connection between coding orientation and mathematical process, since constituents of the text with a naturalistic coding orientation often do offer mathematics as an operational process. There is an important distinction between these two analytical layers, however. The analysis of processes only concerns mathematical processes. If someone is buying paint, for example, that is a naturalistic coding orientation, but no mathematical process is present unless mathematics is used to do something (operational process) or some mathematical relation is made apparent (relational process). Operational processes are typically expressed when mathematics is used to get to know something or to get a result of some kind. Relational processes are typically expressed when mathematics is offered as a coherent system of relations represented as mathematical facts or properties. Images with operational processes are characterised by sequential order and, for example, arrows or shading, whereas images with relational processes offer unchanging conceptual relations, for example in tree structures and analytical relationships. Also, mathematical notation can express operational processes, such as when the equals sign signals “compute”, in contrast to an equality presenting a relation. In summary, the analysis of mathematical processes visualises the nature of the mathematics that the reader is invited to engage with, whereas the analysis of coding orientation reveals how the mathematics is framed or in what context it is implemented.

In the analysis of the logical layer a few aspects that are central to the concept of proportionality were first identified and selected. These are relation, initial value, constant of proportionality and linearity, as well as all feasible synonyms and expressions of these aspects in various semiotic resources and modalities. We focus on three types of expansions in relation to the concept: logical expansion, expansion by addition, and extension. A logical expansion is expressed when a central aspect of a concept occurs twice and the second instance is justified by a reason, a condition or a comparison. Examples of logical expansion are the use of terms such as “thus” or other ways of drawing conclusions from previously given information. For example, in the statement “The function y = 6x is thus a linear function”, the word “thus” contributes to a logical expansion. The second type of expansion is expansion by addition which means that new information on a central aspect is added. This type of expansion does not require any explicit logical connection to the previous information; instead it is about introducing or adding new facts or a new context. New related content might also be expressed by another semiotic resource, for example a formula or a graph, but if the same central aspect is expressed by a new semiotic resource, it is categorised as an extension, the third type of expansion. Extensions are expressions that provide more information about the same thing, such as examples or reformulations, often expressed using another semiotic resource. The results regarding the four analytical layers were noted for all elements in all teaching platforms.

To ensure reliability in the analysis, a pilot analysis of another content area (probability) was initially carried out. For the main study, the coding in step two was first performed by the two authors together for one teaching platform. The coding of the remaining teaching platforms was divided between the two researchers, with each platform being coded by one of the researchers. During the work, there was ongoing discussion about unclear cases. An initial version of the compilation was made by one of the authors and later reviewed by the other author. Conclusions were formulated jointly. During the process, the teaching materials were repeatedly compared with the results and conclusions to ensure reliable analyses.

Results

In this section we present the results structured according to the three different parts of the teaching materials: theory, examples and tasks. For each part, the findings from each of the four analytical layers are described, supported by examples from the teaching platforms. Finally, we summarise the main findings of the analysis regarding how various modalities and dynamic functions are used to express aspects of mathematics in the seven analysed digital teaching platforms.

Modalities and dynamic functions in theory parts

There are some dynamic functions in the theory parts, for example boxes (i.e., content displayed after clicking) that give definitions of concepts such as “graph” or “function”, sometimes together with images. In all analysed definition boxes, the explanations are rather condensed, with formal descriptions expressed in technical language as relational processes. More ample descriptions, perhaps relating to everyday contexts with a naturalistic coding orientation, are not used in these rather brief boxes. The boxes do, however, contribute easily accessible definitions without disrupting the presentation.

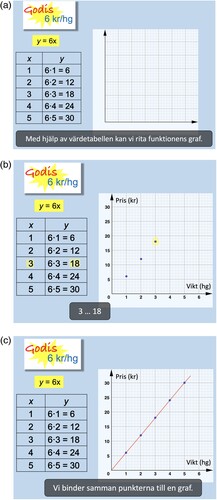
Four of the seven analysed theory parts include films, making films the most common dynamic function in the theory parts. They either take the form of an ordinary lecture, or are made up of static representations that appear and disappear consecutively, supported by oral explanations. The films are largely variants of the theory presented in written text, and can thereby be chosen instead of static text without missing essential content. An advantage of films, not available in static text, is that a film can provide a vivid real-life context, making it possible to connect mathematics with real-life situations outside the classroom. One example from the analysed teaching platforms shows a display counter in a candy shop (Figure 1), accompanied by a voice-over describing two people shopping there. This context is then used for calculations of proportionality through a description of the price of the chocolates. After the presentation of the context, the naturalistic coding orientation is abandoned in favour of technical expressions with mathematical notation, tables and graphs, in addition to the spoken voice-over.

Figure 1. Naturalistic image from a film (TP5).

Other affordances of the film mode that were identified in the analysed films are exemplified in Figure 2. In this example, expansions of central aspects of proportionality are displayed stepwise, starting with an empty coordinate system followed by a graph that emerges dynamically and sequentially in a way that would not have been possible on a static screen or in a textbook. This stepwise emergence provides a logical expansion of central aspects of the concept. The voice-over and subtitles in the film add further expansions which are not represented spatially, one after another as in written text, but temporally. The expansions in the film are also simultaneously highlighted (yellow). The film thus contains a synergy of various semiotic resources and modalities, providing support for students’ understanding of the concept. The sign in the film advertises “Candy 6 kr/hg”. Subtitles are translated in the following paragraph.

Figure 2. Diagrams visible in a film (TP6).

A dynamic function that is present in all the analysed films is that the students can listen to a voice-over as a complement to what is displayed on the screen. In some of the films, the voice-over also adds information not expressed visually. Such added information includes, for example, explanations where the student is personally addressed with the word “we” (Figure 2a: With the help of the table we can draw the graph of the function) or operational processes (Figure 2c: We connect the points to make a graph). This information is not given in the diagrams. In this way, the films add support in the form of operational explanations of the relational descriptions expressed in the written text and in tables, graphs and formulas. The personal address in the voice-over also expresses a closer personal relation with the student, and the ability to provide this kind of support distinguishes the film from the written text.

Modalities and dynamic functions in examples

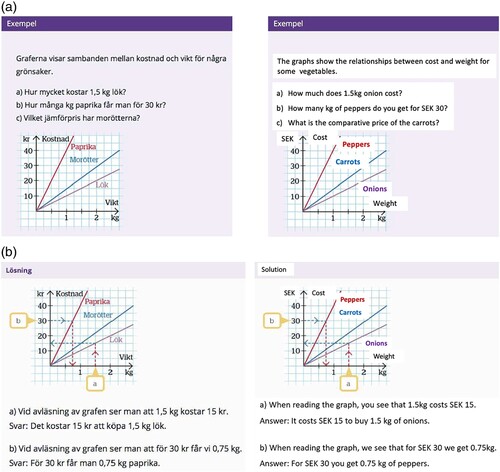
The examples in the analysed teaching platforms are in most cases static, and, as in the theory sections, films predominate when it comes to dynamic functions. The films provide variation in content presentation in terms of coding orientation, processes, and logic in the same way as the films in the theory sections described previously. Another fairly frequent dynamic function is boxes where students can access a solution by clicking (Figure 3). The solutions are answers to example tasks with more or less developed explanations. In some cases, a complete solution is displayed after clicking, while in other cases a hint is presented first, followed by the correct answer. The hint might, for example, inform the student that it is possible to find the right answer in a given graph, as in Figure 6 futher below.

Figure 3. Example and solution accessed by clicking (TP7).

In conclusion, the dynamic functions in the examples are mostly limited to options to show solved examples, and the possibilities for students to interact are therefore small.

Modalities and dynamic functions in tasks

Dynamic functions are utilised to a greater extent in the tasks than in the theory and example parts of the platforms, and the variation in dynamic functions is also greater.

None of the analysed teaching platforms used dynamic functions in the presentation of tasks, for example when presenting a problem in a real-life context in a film, except for a clickable path to where the theory connected to the current task is explained. The dynamic functions are only offered in relation to the students’ completing of the tasks. Together with multiple-choice tasks, the most common dynamic function is a request to write one or a few words as an answer. In some cases, there are opportunities to enter longer or more detailed solutions, to fill in values in a table, or to copy and paste material, for example tables or graphs, from other programmes.

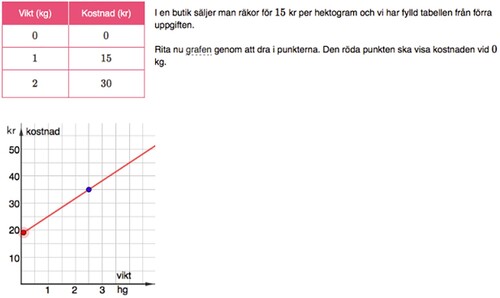
In some teaching platforms, students in the process of solving tasks were offered “laboratory work” with dynamic functions where, for example, they are supposed to move objects or write formulas in a dynamic applet such as GeoGebra. In the example in Figure 4, the student is to drag and move points in a graph. The text in the task says: In a store, prawns are sold for 15 kr per hectogram, and we have filled in the table from the previous task. Now, draw the graph by dragging the dots. The red dot is supposed to show the cost at 0 kg.

Figure 4. Dynamic and interactive example (TP2).

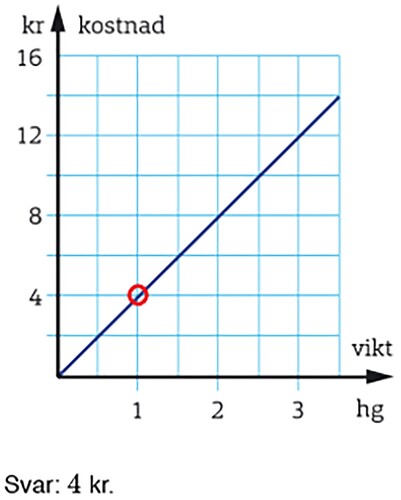
Dynamic functions are also used to provide feedback on solutions in different ways and to different degrees. In some platforms, a pre-made response, or a full solution, is accessible by clicking. In others, it is possible to get instant feedback when the answer is entered. The response can be just right/wrong feedback or a presentation of the correct answer. Some platforms offer model solutions which the students are asked to use to evaluate the accuracy of their solutions. If the feedback is given successively, learning opportunities may increase. In a task Find out the price for one kilogram (Figure 5) the students can, by clicking, access a graph with a red circle showing how to find the price per kilogram. Such a response, easily accessible in a box, can foster a deeper understanding than if only the right answer, 4 kr, is offered. The graph and the answer both appear together, however.

Figure 5. Example solution (TP2).

Teaching platform 2 (TP2) offers several consecutive tasks where responses to the students’ activity with the diagram are offered in a stepwise fashion. In one task the student first has to (1) drag a point in the diagram, and (2) write an explanation of how he or she was thinking and why the point was moved the way it was. In the next step, (3) the student is offered a pre-formulated example solution. The student can thus assess his or her own solution and (4) choose “wrong” / “partly correct” / “correct” in a scrollbar. This dynamic and stepwise support is an example of added value that the digital platform brings.

When it comes to coding orientation, naturalistic language is often initially used in tasks and examples to provide context in a similar manner as in the theory parts. Despite this naturalistic context, the expected answers and the presented solutions are often technical. Naturalistic interpretations or explanations of these technical solutions are neither demanded nor offered. For example, in relation to proposed solutions, students have to evaluate the quality of their solutions themselves, and they need to perform the translation from the naturalistic context of the task to the technical expressions in the solution without support.

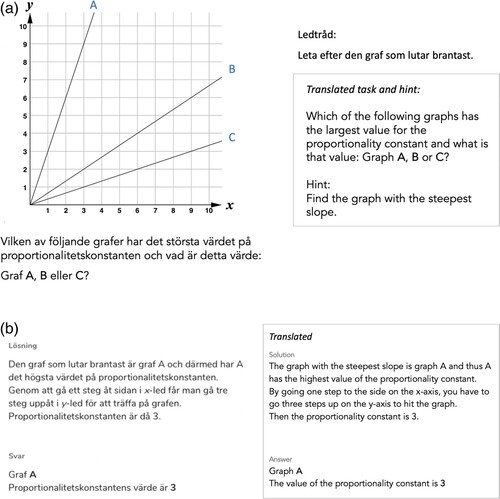
Regarding processes, there is a recurring pair in the tasks: an operational process in a naturalistic context coupled with a relational process expressed technically. To aid the interpretation of technically expressed mathematics, hints offered in boxes can be useful. The analysis highlights that such hints must be carefully designed to fulfil such a purpose. The task in Figure 6 is to find out which graph has the largest value of the proportionality constant, and what that value is.

Figure 6. Task with hint in a box followed by a detailed explanation of the solution (TP5).

The hint (Figure 6), accessible by clicking, suggests finding the graph with the steepest slope. This hint offers operational guidance, but misses the opportunity to support the student in developing an understanding of the mathematics covered by the task, because the hint guides the student rather instrumentally. A detailed explanation is offered in the subsequent example solution, which the student can reach by clicking a second time. This solution switches between a relational description of what defines a high value of the proportionality constant, and an operational explanation of how to find the proportionality constant of a graph.

Discussion and conclusions

Digital teaching materials, such as digital teaching platforms, are on the rise. As noted by Byun and Joung (2018), for example, it is important that digital teaching materials are carefully designed so that opportunities for the students to improve their mathematical proficiency are not passed over in favour of the digital functions. In this study, we have investigated how digital teaching platforms in mathematics make use of the affordances provided by various modalities and dynamic functions. Based on the analytical model forming the basis for the study, we have also discussed potential consequences of different design choices and possible affordances of the dynamic medium that are not fully utilised. The analysis of how aspects of mathematics are expressed by dynamic functions in seven Swedish teaching platforms has revealed that.

• rich learning opportunities can be provided through variation in coding orientation and mathematical processes, and clarity in the logic of mathematics in dynamic functions,

• there is a tendency to present the theoretical part in the form of written or dynamic lectures and to allocate interactive activities mostly to the tasks, and

• dynamic functions provide great opportunities to adapt the presentation to the needs of different students.

The analysis shows that films, animations, information boxes and drag-and-drop exercises entail increased opportunities to express the mathematical content in varied and meaningful ways. For example, the film mode adds possibilities to open up the classroom and expand it to encompass the world outside using a naturalistic coding orientation. A naturalistic film can enable the teaching to move through time and space, entering and leaving contexts outside the classroom where mathematics can be put into realistic contexts. Harvey and Averill (2012) describe the benefits of linking mathematics teaching to real-life situations that may engage students. By means of the film mode, the teaching can be linked to such a context and can also switch between this and an intra-mathematical technical presentation of the subject. Managing the transition between “the mathematics” and the real-world situation, in both directions, is part of a modelling competence, and there is potential to use digital functions to further support the development of such competence.

Another potential of film as a medium is that a film may contain an authentic voice-over or a visible person who addresses the student directly. The voice-over also affords a possibility to add logical expansions of the content that are not displayed on the screen, or operational explanations of relational expressions, which according to previous research can be an important step in the development of mathematical understanding (Rittle-Johnson et al., 2001, 2015). In films it is possible to add arrows, formulas, colour markings and parts of a table or a diagram sequentially, to emphasise that the logic of the content is temporal, as opposed to the spatial presentation in written text, and such sequential presentation can aid with interpretation.

A prominent but perhaps not surprising result of the study is that dynamic functions are used relatively sparsely in theory and example parts. In these parts, examples of exercises where the student is invited to interact actively with mathematics, perhaps by performing a drag-and-drop activity or changing the value of a variable and observing a change in a diagram, were absent. The solved examples could be presented more interactively, for instance by including options to choose solution methods, or adding prompts to reflect on the solution process. Thus, including more functions that are dynamic could lead to a more individualised body of material. An exception to the predominantly static presentation of the theory is the film media, which is present in the theory parts of several of the analysed platforms. Noteworthy, however, is that frequently choosing film as dynamic element causes opportunities for interaction to be lost. Regardless of whether the theory is presented as static text or as a film, these parts mainly have the traditional form of a lecture, and very few opportunities are offered for students to interact with the mathematics. Therefore, the advantages of offering, for example, richer visual and kinaesthetic experiences (e.g., see Baccaglini-Frank, 2021) while teaching new content are missed. Previous studies (e.g., Pepin et al., 2017) describe how dynamic functions are often used in theory instruction to engage students, but very few such functions were identified in our analysis. Another example of missed opportunities to utilise dynamic functions is that films or animations do not occur in the analysed tasks. Here we see opportunities to develop the support offered to the student by providing questions or prompts in films.

The results also reveal that dynamic functions can play an important role in adapting the teaching to different students. For example, dynamic functions such as voice reading, drag-and-drop exercises, and films can complement the static text through their inherent possibilities to offer variation in coding orientation, to provide additional support by clarifying the logic of a task or concept, or to alternate between operational and relational processes. Another relatively common dynamic function that contributes possibilities to adapt the teaching to students’ individual needs is that different parts of a text can be hidden or shown when needed, something that is not possible with a printed textbook. Additional explanations and examples are thus available, but can also be hidden to give a better overview of the content. It has been shown that adaptation of teaching material to users’ particular needs can lead to increased learning (Wang, 2014) and, at least in part, such adaptation can preferably be done by the reader, aided by easily accessible dynamic functions.

Digital teaching materials demand new types of reading skills, but the dynamic features can also provide support with reading. One example is the possibility to allow for a non-linear organisation of the material, where students to some extent can construct their own reading path and, more or less independently, decide what to read and in what order. Digital teaching materials can also provide reading support through functions such as voice reading or by offering passages of text that emerge stepwise on the screen. Another option utilised in the analysed material is, instead of offering the theory solely as written text, to provide a film with similar content or a drag-and-drop exercise that does not require reading, as an alternative. The use of such a dynamic function can thus result in an activity that is markedly different than when using printed textbooks. The student can easily try out potential solutions and evaluate the results. The ease with which the user of digital materials can click through tasks does however also involve a risk of inattentive use and missed learning opportunities (e.g., see Zeynivandnezhad et al., 2020; Bartelet et al., 2016). Therefore, what is suggested here is to implement dynamic features that the student can use to manipulate and explore mathematics in the theory and examples parts, instead of just presenting a lecture-like presentation.

In summary, the analysis shows great potential for integrating different dynamic functions and using their inherent resources to switch between different coding orientations, processes and ways of expressing mathematics in a logical way. However, the potential that we have seen in the dynamic functions is far from fully utilised in the analysed teaching platforms. Instead, the results highlight a substantial remaining influence of traditional conceptions of how mathematics teaching materials should be designed and, as a consequence, a risk that valuable affordances of the digital media will be missed. Digital teaching platforms in mathematics are still “young”, and the limited use (in types and extent) of dynamic functions is likely to be due to both development issues (multiple-choice tasks and films are easily incorporated) and to traditions adopted from printed books (teaching theory in lectures). This means we look forward with great confidence to the future development of digital teaching platforms.

Acknowledgement

We would like to thank the publishers of the mathematics teaching platforms from which the examples were taken for their permission to publish portions of their material.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by the Swedish Research Council [grant number 2019-05005].