Developing algebraic reasoning in primary school using a hanging mobile as a learning supportive tool / El desarrollo del razonamiento algebraico en educación primaria utilizando una balanza como herramienta de apoyo

Abstract

In this study, we investigated the development of algebraic reasoning in 65 fifth-grade students who never had algebra instruction before. In the six-lesson teaching sequence on solving linear equations, a hanging mobile, a physical balance model, played the central role. We expected students’ perceptual-motor experiences with this hanging mobile to be beneficial for the development of their reasoning related to linear equation solving. To investigate how students’ reasoning developed, we analysed videos of classroom interactions, students’ written work during the lessons and students’ responses to lesson-specific assessment tasks. Our results reveal that students showed progress in their level of algebraic reasoning and in their writing down of strategies. While working with the hanging mobile, students applied algebraic strategies such as restructuring, isolation and substitution. They later used these algebraic strategies for solving linear equations in new contexts. This suggests that the experiences students gained in the embodied learning environment provided a basis for algebraic reasoning, which appeared to support them when solving systems of symbolically presented linear equations.

Resumen

En este estudio investigamos el desarrollo del razonamiento algebraico con una muestra de 65 estudiantes de quinto curso de primaria que no habían recibido clases de álgebra con anterioridad. Se aplicó una secuencia de enseñanza de seis lecciones sobre resolución de ecuaciones lineales en la que un móvil colgante, un modelo de balanza física, desempeñó un papel clave. Esperábamos que las experiencias motoras y sensoriales de los estudiantes con la balanza serían positivas para el desarrollo del razonamiento relacionado con la resolución de ecuaciones lineales. Para investigar cómo se desarrolló el razonamiento de los estudiantes, analizamos vídeos de las interacciones en el aula, así como los trabajos escritos de los escolares durante las clases y sus respuestas a tareas específicas de evaluación. Nuestros resultados revelan avances en el nivel de razonamiento algebraico de los estudiantes, así como en la expresión escrita de sus estrategias. Trabajando con la balanza, los estudiantes aplicaron estrategias algebraicas tales como reestructuración, aislamiento y sustitución. Posteriormente, utilizaron estas estrategias algebraicas para resolver ecuaciones lineales en nuevos contextos. Esto sugiere que las experiencias obtenidas por los participantes en el entorno de aprendizaje corporizado les brindó una base para el razonamiento algebraico, que les sirvió de apoyo para la resolución de sistemas de ecuaciones lineales expresadas simbólicamente.

Keywords:

• early algebra
• solving linear equations
• algebraic reasoning
• embodiment
• qualitative data analysis

Palabras clave:

• algebra temprana
• resolución de ecuaciones lineales
• razonamiento algebraico
• corporización
• análisis de datos cualitativos

Early algebra refers to the introduction of algebraic thinking in the elementary grades (Kaput, Carraher, & Blanton, 2008) and aims for building a foundation for providing students access to more advanced algebraic concepts in later grades (e.g., Carraher & Schliemann, 2014). Early algebra does not simply mean ‘teach algebra earlier’ and teaching formal algebra to young students (Carraher, Schliemann, & Schwartz, 2008). Instead, algebra is conceived as a longitudinal strand of thinking and problem solving, starting in kindergarten and continuing in the higher grades (e.g., Kaput, 2008). Early algebra entails a number of big ideas such as equivalence and equations, variable and proportional reasoning (Blanton et al., 2015). From early on, students can be involved in problem-solving activities related to these ideas by drawing on their existing knowledge of skills and procedures in the domain of number (Blanton et al., 2007). Furthermore, it takes students’ everyday experiences and their ‘intuitive and informal ways of reasoning’ (Stephens et al., 2017, p. 143) as the basis for eliciting and developing algebraic thinking that is, for example, necessary for solving elementary linear equations. In this article, we describe how, through participating in embodied activities over the course of a six-lesson teaching sequence on linear equation solving, elementary school students developed context-based algebraic strategies which ultimately enabled them to solve a system of two linear equations with two unknowns.

Linear equation solving

The main characteristic of an equation is that the expressions on both sides of the equal sign represent the same value. In this sense, both sides of the equation are equal — though they might look different. In the process of solving an equation, this equality should be maintained. Equality is therefore deemed a key concept in linear equation solving (e.g., Bush & Karp, 2013; Knuth, Alibali, McNeil, Weinberg, & Stephens, 2005; Li, Ding, Capraro, & Capraro, 2008). Understanding this concept is one of the main demands when solving linear equations (Kieran, 1997; Kieran, Pang, Schifter, & Ng, 2016).

When solving an equation, the goal is to find the value(s) of the unknown(s) for which the expressions on both sides of the equal sign are equal. This goal can be reached by isolating the unknown. In order to achieve this, students have to operate with the expressions in such a way that their equality is maintained. This is often emphasized by referring to the metaphor of the equation being in balance (Ngu & Phan, 2016) and implies performing transformations under the principle of ‘doing the same to both sides’. Among other things, this involves the preparatory activity of restructuring the given equation by, for example, changing the order of the terms in the expressions by using the commutative and associative properties, replacing expressions by equivalent expressions, or exchanging the two sides, which is possible due to the symmetry of the equality. At a formal level, this restructuring can entail notating unknowns in an expanded (e.g., A + A) or condensed (e.g., 2A) way. Further simplifying an equation to isolate the unknown can, for example, be done by taking away the same elements from both sides or by halving the expressions on both sides. A less targeted method for solving equations is guessing-and-checking. This implies that different values for an unknown are put in an equation until the correct answer is obtained (e.g., Stacey & MacGregor, 1999).

When solving a system of linear equations with multiple unknowns, the information from more than one equation has to be used to find the values of the unknowns. In this case, the isolation method can be applied by eliminating one unknown by means of, for example, subtracting one equation from the other. Yet, the most prominent method to solve a system of linear equations with multiple unknowns is the method of substitution (replacing an expression with another expression of the same value).

Crucial in using these strategies is that students have a good understanding of the concept of equality and the properties of operations. Many of the difficulties students experience when solving (systems of) linear equations have to do with an incorrect interpretation of the equal sign. Students consider it as a symbol for ‘here comes the answer’ or as a sign to ‘add’ (e.g., Behr, Erlwanger, & Nichols, 1980; Carpenter, Franke, & Levi, 2003), instead of as a symbol reflecting the sameness of the expressions on both sides (e.g., Knuth, Stephens, McNeil, & Alibali, 2006). This latter, proper conception of the equal sign as a relational symbol is positively related to competence in solving linear equations (e.g., Alibali, Knuth, Hattikudur, McNeil, & Stephens, 2007; Knuth et al., 2006; Matthews, Rittle-Johnson, McEldoon, & Taylor, 2012). Other well-known difficulties for students related to linear equation solving are difficulties with understanding the formal, symbolic representations of equations (e.g., Koedinger & Nathan, 2004) and difficulties with performing operations on the unknowns when solving equations (e.g., Filloy & Rojano, 1989; Herscovics & Linchevski, 1994).

Teaching linear equation solving

Approaches that have been developed for teaching linear equation solving are all trying, in one way or another, to overcome the aforementioned difficulties. Within Realistic Mathematics Education (RME) (see, e.g., Van den Heuvel-Panhuizen & Drijvers, 2014), this means starting with meaningful situations in which the students can solve informal equation-like problems with context-connected strategies and then, through a process of progressive mathematization, come to more formal and standard solution processes. In a study by Van Reeuwijk (1995), students were asked to figure out what a T-shirt cost and what a soda cost, when two T-shirts and two sodas cost $44 and one T-shirt and three sodas cost $30. Students are more prone to solving such a problem that is meaningful to them. When students can make sense of a problem, or in other words, when they can imagine what happens in the problem, it can open their action repertoire for solving it (Van den Heuvel-Panhuizen & Drijvers, 2014). In this case, by halving the first set of T-shirts and sodas, students know what one T-shirt and one soda cost, and then they can find that two sodas cost $8. The strategies of isolation (by elimination) and substitution developed for solving this problem can later be used for solving other systems of linear equations. In other words, the meaningful context of the T-shirts and the sodas can become a model for solving other problems.

In addition to this context model, other mathematical models are used for teaching linear equation solving as well, such as area models, linear models and balance models (Van Amerom, 2002). These models are also meant to help students in understanding what it means to solve an equation and develop strategies to find the values of unknowns. Of these models, the balance model has a long didactical history. It was already used by Leibniz (1646–1716), who mentioned the relation between equality in a mathematical situation and a balance with equal things on both sides (Leibniz, 1989).

A recently conducted literature review (Otten, Van den Heuvel-Panhuizen, & Veldhuis, 2019) showed that in teaching linear equation solving, various appearances of the balance model are used. It can be a concrete physical device, a drawn balance on a work sheet or a virtual balance in a digital environment. These types of balance models, which in some studies are used in combination, each have their own affordances. Concrete balances are chosen because the physical experiences that students can have when working with such a device are considered to be beneficial for the learning process. A recent meta-analysis on the efficacy of using concrete manipulatives for teaching mathematics found small to moderate effect sizes in favour of using manipulatives compared to providing abstract symbolic instruction (Carbonneau, Marley, & Selig, 2013). A theoretical perspective on the working mechanisms behind learning with manipulatives is provided by embodied cognition theory (e.g., Pouw, Van Gog, & Paas, 2014). This theory states that bodily experiences can be advantageous for cognitive learning processes (e.g., Wilson, 2002). Cognition is formed not only by and in our brains, but also by perceptual-motor experiences that we have when our bodies interact with the world (e.g., Gallese & Lakoff, 2005; Wilson, 2002). Therefore, embodied learning environments (short for: learning environments based on embodied cognition theory) are regarded as essential for learning mathematics (Abrahamson, 2017; Lakoff & Núñez, 2000; Núñez, Edwards, & Matos, 1999). By coupling action and perception, perceptual-motor experiences form the basis for the emergence of mathematical concepts and mathematical reasoning, mediated by conceptual metaphors (Lakoff & Johnson, 1980) and representational redescription (Karmiloff-Smith, 1992). In this way, for example, through physical experiences with a concrete balance, students can revitalize their conception of equality and their physical experiences of how to maintain the balance, and may shift both to a more abstract understanding, which is necessary for linear equation solving at a formal level.

Research in which the balance model was used for teaching linear equation solving indeed has shown that the balance model can be helpful for students. Yet, positive results were not found for all types of balance models. The most positive results have been reported for physical balance models (e.g., Perry, Berch, & Singleton, 1995; Warren & Cooper, 2005) and for virtual balance models (Figueira-Sampaio, Santos, & Carrijo, 2009; Suh & Moyer, 2007). For drawn balance models, some studies mainly found positive results (e.g., Araya et al., 2010; Cooper & Warren, 2008) while others reported both positive and negative results (e.g., Linchevski & Herscovics, 1996; Vlassis, 2002), or even only negative results (e.g., Ngu & Phan, 2016).

A characteristic of physical balance models is that they are dynamic, which means that students can operate on them and get real-time feedback on their actions. This, in turn, can help students develop strategies for keeping the scale in balance. However, studies in which a physical balance model was used (e.g., Perry et al., 1995) mostly showed only what equations students learned to solve and scarcely revealed how their algebraic reasoning for equation solving developed. The same is true for the algebraic strategies that were used in connection with their working with the physical model. The present study aims to contribute to knowing more about what an embodied learning environment with a physical balance will bring about in students’ reasoning.

Current study

The study made use of a six-lesson teaching sequence on linear equation solving, based on an embodied cognition theory approach and the RME principle of starting with a meaningful context that can evolve into a model for eventually solving a system of two symbolically presented linear equations with two unknowns. In the teaching sequence, algebraic reasoning was elicited by a number of activities in which students were offered embodied experiences with a physical hanging mobile: a concrete balance model with, on each side, a number of bags hanging on a chain to represent an equation with unknowns. Bags with different colours were used, which each had a different weight (e.g., white = 50 grams, red = 100 grams, black = 150 grams). These weights were unknown to the students. Students were challenged to discover ways to maintain the balance of the mobile while manipulating the differently coloured bags.

We theorized that when students worked with the hanging mobile trying to keep its balance, the pervasive everyday-life experiences of balancing (Gibbs, 2006) could be revitalized and linked to the experiences of maintaining the balance of the mobile, representing equality in a linear equation. In this way, students’ understanding of the concept of equality could be grounded in the bodily based experiences of maintaining balance, which is also in line with Piaget’s statement that children ‘can only “abstract” the idea of such a relation as equality on the basis of an action of equalization’ (Piaget & Inhelder, 1967, p. 43). The possible physical manipulations that maintain the balance of the hanging mobile could act as a metaphorical mapping (Lakoff & Johnson, 1980; Núñez et al., 1999) of the algebraic strategies that can be used to maintain equality in equations. In particular, consider that students’ manipulations of the bags can result in the hanging mobile being in or out of balance. Students, for example, can take away similar bags from both sides of the mobile. By doing this, they feel the similar weights of the bags in their hands and concurrently perceive the beam of the hanging mobile remaining in balance. Thus, students physically experience the principle of ‘doing the same to both sides’, which is an important strategy for solving equations (e.g., Arcavi, Drijvers, & Stacey, 2016). When working with the hanging mobile, students directly perceive the influence of their actions — such as removing bags — on the status of the balance. In line with embodied cognition theory, we hypothesized that these perceptual-motor experiences could promote the grounding of the concept of equality in the bodily based experience of maintaining balance.

Through maintaining the balance of the hanging mobile, students could intuitively apply informal context-connected algebraic strategies which underlie the conventional strategies for solving equations, such as changing the order of the coloured bags (restructuring), taking away bags from both sides of the mobile to isolate bags of one colour (simplification/isolation), and replacing bags with bags of other colours (substitution). We hypothesized that through exploring what could be done while keeping the hanging mobile in balance, combined with a number of challenging tasks, students could come more or less spontaneously to the strategies that form the basis of the key algebraic strategies necessary for solving equations. This approach, in which the students have a main role in learning algebraic reasoning, also reflects the didactics of RME, namely that instead of the teacher transferring the strategies to the students, they are active participants in developing these algebraic strategies.

In this study, our aim was to put this teaching sequence to the test and investigate how students’ algebraic understanding and reasoning develops, and whether characteristics of their algebraic understanding and reasoning are related to what they are offered in the teaching sequence. More precisely, this resulted in the following two research questions:

1. How does fifth-grade students’ algebraic reasoning for solving linear equations develop in an embodied learning environment?

2. How are students’ experiences in the learning environment related to their use of algebraic strategies?

Over the teaching sequence, we expected students to improve their algebraic reasoning for solving linear equations. Moreover, we expected students’ perceptual-motor experiences with the hanging mobile to be beneficial when solving equations in the context of the hanging mobile, in new informal contexts and when they are formally presented. We therefore expected to find references to (experiences with) the hanging mobile when analysing students’ reasoning.

Method

Participants

To answer these research questions, a study was carried out involving 69 students from three fifth-grade classes in three schools in the Netherlands. Two of the schools, a public one and a Catholic one, were situated in urbanized areas, and the third school was a public school situated in a suburbanized area. The study was approved by the ethical committee of the Faculty of Social and Behavioural Sciences of Utrecht University. Active informed consent was provided by the parents of the students. Permission to use the data was obtained for all students except three. These students were excluded from the analyses. One other student was excluded from the analyses because he missed most of the lessons. This resulted in the final number of 65 students: 27 boys (42%) and 38 girls (58%), with ages between 9 and 11 years old (M = 10.02, SD = 0.45). They had received no prior instruction on equation solving or other algebra topics, which is in accordance with the Dutch mathematics curriculum, in which teaching algebra starts in the first year of secondary school.

Materials

Teaching sequence

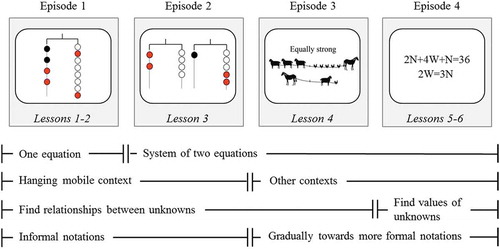
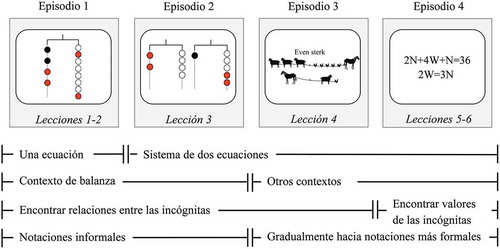
The teaching sequence (see Figure 1) consisted of six lessons. These lessons were clustered in four episodes, each with their own focus and content. In each of these episodes, the aim was to develop algebraic strategies related to linear equation solving.

Figure 1. The teaching sequence and its content.

In Episode 1, students gained physical experiences with a physical hanging mobile. The tilting beam of the mobile could be in or out of balance, thus providing students real-time feedback on their actions while manipulating the bags on the mobile. While students were working with the hanging mobile, the teacher asked questions like: ‘Can you explain why the beam of your hanging mobile is straight?’; ‘Can you explain why the hanging mobile remains straight after the manipulation you just carried out?’; or ‘Would it be possible to remove something from your hanging mobile in such a way that it remains straight?’ During the ensuing classroom discussion, one hanging mobile was positioned in front of the classroom. The students were asked to mention all possible actions they could perform on the hanging mobile while keeping it straight. These actions were carried out on the mobile, and the teacher registered the possibilities on the blackboard, making use of the students’ own wording (e.g., ‘one colour of bags could be changed for another colour of bags’ instead of ‘substitution’). Because students worked with one hanging mobile in this first episode, they were reasoning about one equation.

In the following episodes, the information from two equations had to be combined to discover relationships between unknowns to solve the problems, so that students were reasoning about a system of equations. In Episode 2, problems were still posed in the context of the hanging mobile, both physically and on paper. The teacher started by asking whether it would be possible to combine the information from the two hanging mobiles in front of the classroom, to create a new mobile. After gathering students’ thoughts, the teacher invited a student to manipulate the bags on the two existing mobiles to find a new relationship between unknowns and display that on a third mobile. Then, students worked on paper-based tasks in which the information from two mobiles had to be combined.

In Episode 3, the information from two equations had to be combined to discover relationships between unknowns in new contexts, such as a tug-of-war situation. In this episode, the teacher started with a classroom discussion about the similarity between the new context of the tug-of-war situation and the familiar context of the hanging mobile, namely, that in both contexts it is all about maintaining equality. Then, all possible actions to maintain the balance of the hanging mobile were recalled, before students started with solving problems in the new tug-of-war context. Moreover, in this episode students were gradually challenged to use more symbolic notations, such as letters to notate the strength of the animals participating in the tug-of-war game. This was evoked by asking the students to think about alternative ways to notate their explanations, as such avoiding the time-consuming process of drawing the animals or writing down the entire reasoning process.

In the final episode, Episode 4, instead of discovering relationships between unknowns, students had to find the values of unknowns in a system of two linear equations with symbolically notated unknowns. As an introduction, the teacher again discussed the analogy between the hanging mobile and these new, symbolically notated equations. Moreover, she discussed the meaning of the symbolic notations, leading, for example, to discussions about whether ‘2N’ would be the same as ‘N + N’ or whether ‘1N’ would be an alternative way to notate ‘N’.

During our teaching sequence students encountered many different equations in which different quantities were used. For example, when students were working with the hanging mobile (Episodes 1 and 2), they were working with the quantity of weight (e.g., three white bags are as heavy as one black bag). In the case of the tug-of-war situations (Episode 3), they were working with the quantity of strength (e.g., one sheep is as strong as three chickens). In Episode 4, they were working with objects and prices (one apple and one banana together cost eight euros), and they ended up with formally notated equations with an equal sign and with unknowns presented as letters (M + 3L = 25 and M = 2L), which were not related to a given quantity such as weight, strength and cost per object.

Assessment of algebraic reasoning

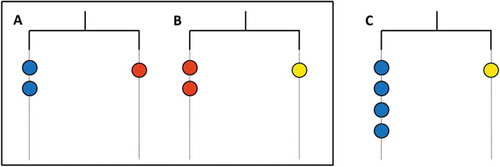
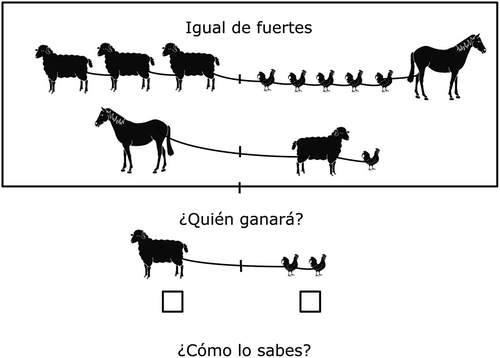
Students’ level of algebraic reasoning related to linear equation solving was assessed by means of paper-and-pencil assessment tasks administered at the end of each lesson (see Appendix A, Figures A1–A3, for examples of the assessment tasks of Episodes 2–4). Each assessment task reflected the goal of the corresponding lesson. The assessment task of Episode 2 contained two balanced hanging mobiles including circles, rectangles and stars, informally representing the formal algebraic equations 3X = Y + 5Z and Y = X + Z. On the basis of these mobiles, the students had to determine for two other mobiles (X = 3Z and 4Z = Y) whether they were balanced. In the assessment task of Episode 3, the same equations were used, but with strawberries, bananas and pears, and with an equal sign instead of a hanging mobile. Lastly, in the fourth episode, students had to solve a system of two symbolically presented equations. In this assessment task, they had to discover the values of unknowns M and L by using the equations M + 3L = 25 and 2M = 4L.

For all tasks, in addition to giving the answer to the problem, students were asked to explain their thinking and thus to reveal their reasoning. Answers were scored as incorrect (0) or correct (1), and this dichotomous scoring was used to calculate the success rate — that is, the percentage correct per assessment task. Students’ explanations were categorized on their level of reasoning by means of a coding scheme (see Data analysis).

Procedure

The 50-minute lessons were each taught in six consecutive weeks by the first author of this article, with the assistance of a teaching assistant during the two lessons of the first episode. Episode 1 took place in a separate room in which five hanging mobiles were positioned. In this episode, students worked together in small groups of two or three students. The remaining episodes took place in the students’ classroom. During each episode, at least one physical hanging mobile was present in the classroom, even in the case that it was not used for instruction. After the first episode, students worked individually, in pairs or in small groups. Individual or group work alternated with whole-class discussions. In between the lessons the students followed their regular programme.

In the first episode, in one class, two pairs of students were video-recorded, so that their manipulations on the physical hanging mobile and their reasoning could be followed more closely. These particular students were recorded because their parents provided permission for this. During the rest of the episodes in this class, the camera was placed in the back of the classroom to give a global overview of the lesson activities. For the other two classes, two pairs of students were video-recorded in the first episode, and also in the following episodes the video-recording of the work and conversations of these students was continued. As such, we could follow these students’ reasoning over time. In addition to the focus on these two pairs of students, from Episode 2 an extra camera was placed in the back of the classrooms to give a global overview of the lesson activities in these two classes as well.

Data analysis

The data consisted of students’ responses to the problems to be solved during the lessons and to the assessment tasks, and audio- and video-recorded interactions. To analyse how students’ algebraic reasoning developed over time (Research Question 1), we focused on the three consecutive episodes in which students solved systems of linear equations (Episodes 2–4). For each episode, the assessment task that was given to the students at the end of that episode was analysed (see Appendix A, Figures A1–A3, for examples).

For calculating the success rate on each of these assessment tasks, a student’s response was scored as correct when both problems of the task were answered correctly. The task belonging to Episode 4 was scored as correct when students correctly reported the value of both unknowns.

To categorize students’ explanations on the assessment tasks, a coding scheme was developed that was applicable to each of the tasks. The development of this coding scheme followed an iterative process, inspired by the constant comparative method (Glaser, 1965). We commenced with a coding scheme on the basis of the work of only a couple of students. This coding scheme was then taken as a starting point to code the remainder of the data. When examples of student work were encountered that did not fit into the existing scheme, the scheme was adapted. As such, the final coding scheme was established after several rounds of careful examination of the data and the reaching of consensus between the researchers. Subsequently, there was a final round of coding in which all data were recoded on the basis of the final coding scheme.

In each assessment task in Episodes 2–4, students had to solve the problem by reasoning on the basis of a given system of two equations. In the final coding scheme, we distinguished between students who did not use any of these equations in the description of their reasoning (Level R0), students who reasoned on the basis of only one of the two given equations (Level R1) and students who reasoned on the basis of both given equations by combining the information of both of them (Level R2). Within the Levels R1 and R2, we furthermore distinguished between (1) students who did not make clear how they came to their answer or which strategies they used, and (2) students who did give this information. The coding scheme, with examples of students’ responses for each assessment task and each level of reasoning, can be found in Appendix B.

Additionally, for each episode, the association between students’ level of reasoning and their success rate was evaluated by means of a chi-square test of independence.

To analyse the possible relation between the affordances of the embodied learning environment and students’ development of algebraic reasoning (Research Question 2), we looked into the algebraic strategies elicited in each episode by analysing students’ written work and the video- and audio-recorded interactions, and searched for events in which students made use of algebraic strategies when solving the problems in the classroom. In this way, we could relate the students’ strategy use to what happened in the lessons during that particular episode.

Results

Students’ development of algebraic reasoning in an embodied learning environment

In the course of the teaching sequence, students more often provided the correct answer as shown by the increase in the success rates on the respective assessment tasks, from 44% in Episode 2, through 57% in Episode 3, to 77% in Episode 4. Furthermore, students’ level of algebraic reasoning increased over time, as shown in Figure 2. The percentage of students showing reasoning without using the given equations (Level R0) decreased, from 57% in Episode 2 to 20% in Episode 4. Students who showed this type of reasoning provided, for example, the explanation that they ‘just knew the answer’, provided a general description that they ‘looked at the example’ without stating explicitly which information was used to come to that answer, or did not write down anything. The percentage of students that showed reasoning reflecting the use of only one of the given equations (Level R1) remained more or less stable, between 23% and 28%. Julia’s answer on the assessment task of Episode 2 (see Appendix A, Figure A1) is an example of reasoning which was categorized as Level R1. She assigned values to the unknowns on the basis of the second given equation alone, while ignoring the information from the first equation. Finally, the percentage of students that showed reasoning in which both given equations were used (Level R2) increased over time, from 17% in Episode 2 to 52% in Episode 4. Julia’s reasoning on the assessment tasks of Episodes 3 and 4 (see Appendix A, Figures A2 and A3) are two examples of this level of reasoning. For example, on the assessment task of Episode 4 (see Appendix A, Figure A3), she first transformed the equation 2M = 4L into M = 2L. Subsequently, she used this information to substitute the unknown M in the other equation by 2L. In this way, she combined the information of both given equations to come to an answer, which belongs to reasoning Level R2.

Figure 2. Percentages of students performing at a level of reasoning over the three episodes (N_{Episode 2} = 63; N_{Episode 3} = 65; N_{Episode 4} = 61).

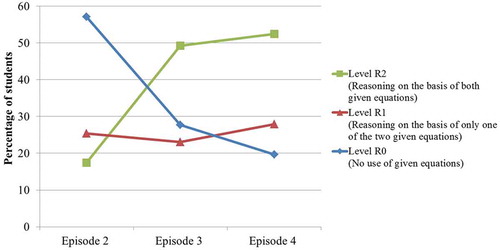
The association between students’ level of reasoning and their success rate differed between the episodes. In Episode 2 (χ² (2, n = 63) = 2.37, p = .306) and Episode 3 (χ² (2, n = 65) = 5.97, p = .051), providing a correct answer was unrelated to students’ demonstrated level of reasoning, while in Episode 4 (χ² (2, n = 61) = 8.70 p = .013), a high level of reasoning occurred more often with a correct answer and a low level of reasoning with an incorrect answer.

Additionally, the development in level of reasoning was analysed for each student individually. One student was excluded from this analysis, because she was absent for two of these three assessment tasks. In total, 31 students (48%) showed a pattern of reasoning which improved at least one level over time, while no decline was shown. The level of reasoning of four students (6%) only decreased. Fourteen students (22%) showed reasoning that remained at the same level over time. Finally, the remaining 15 students (24%) showed a fluctuating reasoning pattern, which over time was both increasing and decreasing.

In addition, we also found that there was an increase in the number of students who were able to write how they derived their answer and/or show their applied strategies when solving the problems. This was especially the case for the students in Level R2. Whereas in Episode 2, 16% of the 63 students who belonged to Level R2 gave a description of their reasoning, this percentage increased to 42% for the 61 students involved in Episode 4. For the students performing at Level R1, these percentages ranged from 17% in Episode 2 to 12% in Episode 4.

Relation between the students’ experiences in the learning environment and their use of algebraic strategies

Episode 1: physical experiences with the hanging mobile

In the first episode, all students started with the same, balanced, physical hanging mobile (see Figure 1, Episode 1). Students were not provided with information about how the bags were related. In the first task, students were asked to change the hanging mobile in such a way that it would look different, but would still be hanging straight, while using the same bags. This led students to use different restructuring strategies. For example, Eva commented, as follows, to her partner Jailey:

Table

Eva: We can do exactly the same, but then on the other side. So these bags	[1]
[points to the bags on the left side] to the other side, and these ones [points to the	[2]
bags on the right side] also all to the other side. So all these bags to that side and	[3]
all these bags to the other side as well. Then it is different, but also the same	[4]
[laughs]!	[5]

Another restructuring strategy was shown by Iris and Zara. They changed the order of the bags on the right side of the hanging mobile by grouping them by colour. Kees and Julia also restructured their hanging mobile, but instead of exchanging all the bags from one side to the other or grouping them by colour, they brought three white bags to the left side of the mobile and in exchange one black to the right side. The restructuring strategies identified by the three pairs of students already in their first attempt working with the hanging mobile correspond to important algebraic strategies. Eva and Jailey’s strategy of exchanging all the bags between the sides of the hanging mobile corresponds to the symmetry property of equations (a = b ≤> b = a). The strategy of Iris and Zara, who changed the order of the bags on one side of the hanging mobile, reflects the commutative law of addition. Kees and Julia discovered how the white and the black bags are related and applied already a substitution strategy in restructuring the composition on their hanging mobile. This last way of restructuring was actually shown by most groups of students when working on this task.

After a short group discussion about the resulting compositions on the hanging mobiles after the transformations, students were tasked to find everything that could be done while keeping the hanging mobile straight, and this time they were also allowed to add bags and take away bags. The following conversation between Kees and Julia exemplifies the emergence of their use and understanding of the isolation strategy, by first removing identical unknowns from both sides of the equation (Lines 6–7) and then removing different unknowns from both sides based on the ratio (Lines 9–10). Furthermore, in the second part of the interaction in their discussion with the teacher (T), their use of the substitution strategy is exemplified, as they describe it in words (Lines 13–15) and illustrate it by physically substituting bags on the hanging mobile (Lines 24–25).

Table

Kees: These two [points to the two red bags on the left side] are the same as	[6]
these two [points to the two red bags on the right side]. They are equally heavy …	[7]
Julia: … so then it must be that these two blacks are the same as 1, 2, 3, 4, 5 …	[8]
6 [white bags] [counts the white bags on the right side of the hanging mobile]! So	[9]
then one [black] equals three [whites]	[10]
Kees: Yes!	[11]

A little later, they had created a balanced hanging mobile with, on the left side, two black bags and, on the right side, two white and two red bags.

Table

T: Can you tell me why this hanging mobile is straight?	[12]
Kees: Because this one [points to one red bag] counts for two whites [a ratio	[13]
they had previously discovered]. And three whites together equal one black. So	[14]
one red and one white together must be one black.	[15]
T: [looks at Julia] Do you agree?	[16]
Julia: Yes!	[17]
T: So, you actually say, if I would replace this one [points to one red bag] with two	[18]
whites …	[19]
Kees: … it’s exactly the same!	[20]
T: Yes? Are you sure?	[21]
Kees: [nods]	[22]
T: Let’s try!	[23]
Kees: [replaces one red bag with two whites and watches the mobile coming back	[24]
into balance, see Figure 3] Look!	[25]

Figure 3. Kees and Julia substitute a red bag for two whites and watch the physical hanging mobile coming into balance (Episode 1).

In these activities, maintaining the balance of the mobile represents maintaining equality in an equation. The interactions clearly illustrate that students used different algebraic strategies, with which they were gaining perceptual-motor experiences. By restructuring the mobile through exchanging all the bags from one side to the other, the students could physically experience that both sides of the equation are interchangeable and that changing the order of the bags on a side does not disturb the balance. Moreover, by taking away similar bags on both sides, the students could physically experience the possibility of cancelling identical terms from both sides, which can be used to isolate particular unknowns. The third strategy, the substitution strategy, allowed the students to further simplify the composition on the hanging mobile, thus bringing them closer to finding all the ratios. By means of the real-time feedback the tilting beam of the hanging mobile provided, students were constantly able to verify, and if necessary adjust, their reasoning, which was for example shown by Kees and Julia when replacing the red bag with two white ones (Lines 24–25).

After students worked with the physical hanging mobile in small groups, in the classroom discussions students shared experiences. During these discussions it came to the fore that most groups of students shared the experience of maintaining balance by using similar strategies.

Episode 2: combining the information from two hanging mobiles

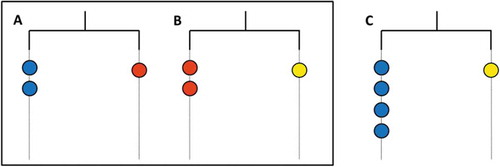
Next, the students were given a task in which they had to combine the information from two hanging mobiles, with the goal of fostering their further development of algebraic strategies, in particular the substitution strategy. The teacher introduced the task by placing three physical hanging mobiles in front of the classroom (see Figure 4).

Figure 4. Three hanging mobiles in front of the classroom (Episode 2).

In one classroom, Florien raised her hand when the teacher asked whether it would be possible to combine the two hanging mobiles (A and B) to create the third one (C).

Table

Florien: If you double the red one,		[26]
then it becomes one yellow [points to the hanging mobile A].		[27]
And if you then double the blues as well, it results in four blues.		[28]
So then you know that four blues equal one yellow.		[29]

Florien’s strategy was one of the strategies that also came up in the other classes. She prepared her use of the substitution strategy by transforming the first equation (A) by doubling. This enabled her to substitute one side (two red bags) of the equation as a whole, by making use of the information from the second equation (B). After explaining her strategy to the rest of the class, she made it visible to the other students on the physical mobiles in front of the classroom. A second example of substitution was put forward, in which students, based on the information of the first hanging mobile (A), replaced one red bag in the second equation (B) with two blue bags. So here, instead of substituting one side of the equation at once, one unknown (or element) in the equation was substituted for another unknown. Most students used this strategy. Finally, instead of replacing unknowns with other unknowns, a few students also used substitution of unknowns by values, which was exemplified by Mats. He assigned the value of 1 to each blue unknown, the value of 2 to the reds and the value of 4 to the yellow unknowns, which resulted in both sides of each equation adding up to the same number. Although Mats did not explain how he came to these values, his choice for the particular values evidenced that he took all equations into account.

Episode 3: a new context

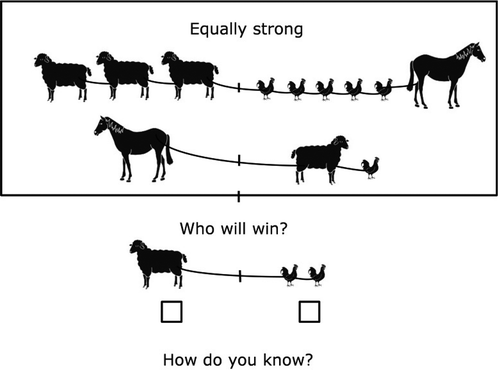
In this episode, the students were presented with problems that were far away from the problems with the hanging mobile, but nevertheless had some similarity with them. Two groups of animals played a tug-of-war game, and the question was which group would win (see Figure 5). Also, here the focus was on the equality of both sides and figuring out which group was stronger by applying all kind of transformations while keeping the balance.

Figure 5. Tug-of-war problem (Episode 3).

Milan explained his strategy for solving this problem to the rest of the class. First, he combined both equations by adding them, as such creating one new equation (Line 30). Subsequently, he applied isolation strategies to solve the equation, by first taking away a horse on both sides (Lines 30–31), then a sheep on both sides (Lines 31–32), and then by removing different unknowns based on the ratio by dividing both sides of the equation by two (Line 33).

Table

Milan: I added the lower row to the upper one. Then I was able to take away both	[30]
horses. Then on the right side, six chickens and one sheep remained. So, you	[31]
could take away a sheep at both [sides]. Then there are six [chickens] and two	[32]
sheep left. Dividing makes three [chickens].	[33]

Julia used another strategy for solving this problem. She first converted the problem into two equations with letters, by writing S + S + S | C + C + C + C + C + H and H | S + C. Then, she substituted the H in the first equation for a C and an S, resulting in S + S + S | C + C + C + C + C + C + S. Subsequently, to isolate the chickens, she crossed out the S on both sides, and lastly she crossed one S on the left side and three Cs on the right side, leaving S | C + C + C. She rewrote this as ‘1S = CCC3’. A third strategy that again some students used to solve the problem was assigning values to the unknowns, which was already described in Episode 2.

In this episode, where the students were presented with equation-like problems in a new context, again different strategies for combining the information from both equations came forward. Milan (Lines 30–33), for example, added both equations to create a new equation with some identical unknowns on both sides that he could take away, to subsequently isolate one unknown and express it in another. However, Milan was one of the few students that used this smart way of combining both equations to constitute a new one. Most students used the substitution strategy to solve this problem. This strategy was also used a lot while working with the physical hanging mobile. In Episode 3, this strategy was, for example, shown by Julia, who converted one type of unknown (the horse) to two other types (a sheep and a chicken). She also used this process of substitution of one type of unknown into other types when working with the physical hanging mobile in Episode 1 (Lines 9–10).

The strategies that came up in this episode to solve the new type of equation-like context problems are equivalent to the strategies the students had developed while working on the hanging mobile. When explaining their answers, some students explicitly referred to their experiences of working with the hanging mobile, for example, through expressions such as ‘the horse can be seen as a green bag’. In one classroom, when the teacher did not pay attention for a short time, the students even used the coloured bags of the hanging mobile, which were not used at that moment, to represent the tug-of-war situation on their table. Additionally, students often explained their solving strategies in terms of actions, such as ‘I replace the horse by a sheep and a chicken, then I take away a sheep on both sides, and then I take half of both sides’. The combination of students using similar algebraic strategies, explicitly referring to the hanging mobile context, and providing explanations on solving the problem in terms of actions suggests that students’ experiences of working on the hanging mobile might have formed a foundation for this later stage of solving linear equations in a new context.

Episode 4: solving a system of symbolic equations

In the last episode of the teaching sequence, students were presented with a system of two symbolic linear equations with two unknowns. As discernible in Figure 6, Kees (see also Episode 1) could solve this problem by showing that F = 6 and H = 12. He first converted the equations into hanging mobiles, notating the unknowns in an expanded way. Then, by connecting the Fs on both sides of the hanging mobile, he showed the presence of identical terms on both sides of the equation. Moreover, he crossed these unknowns to reveal the process of cancellation, resulting in the isolation of one F on the right side of the equation. Subsequently he could derive the value of this unknown by solving 19 − __ = 13. Lastly, by substituting the value 6 for the unknown F in the second hanging mobile (representing the second equation), he was able to calculate the value of H.

Figure 6. Kees’ solution of a system of two symbolic linear equations, combined with the answer that F = 6 and H = 12 (Episode 4).

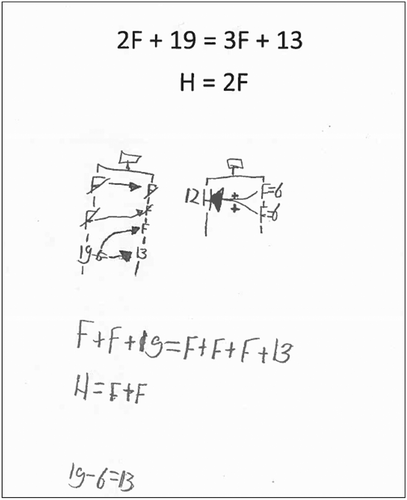
Like Kees, many students first converted the equations into a hanging mobile before showing cancellation of identical terms. Some other students reasoned directly on the basis of the symbolically notated equation. For example, Kira first repeated the first symbolic equation, and then wrote down ‘1F is added’ implying that she noticed that in the first equation on the left side there are two Fs, whereas on the right side there are three. She then reasoned that she could do the subtraction ‘19 – 13 = 6’ to arrive at the value of ‘1F = 6’. Finally, she used this finding to determine the value of H: ‘2F = 12’.

In this last episode, it was revealed that most of these students, who were taught linear equation solving in an embodied learning environment, were able to solve systems of two symbolic linear equations. Most students did not seem to have difficulties with understanding the symbolic way of notating the unknowns. Kees, for example, showed understanding that 2F is an abbreviated way of notating F + F. Nevertheless, he did not solve this problem in a symbolic, formal way. Instead, before applying the isolation strategy and then the strategy of substituting of values, he first went back to the model of the hanging mobile. This is an example showing that at least some students experienced the model of the hanging mobile as a powerful tool that they applied when solving linear equations at a formal level. Some other students, like Kira, reasoned directly on the basis of the symbolic equations.

Kees and Kira, for example, are students who, like most students in our study, did not seem to have difficulties with equations not written in the standard form (e.g., a + b = c), such as equations containing unknowns on both sides of the equation (e.g., 2F + 19 = 3F + 13 or H = 2F). The students did not seem to have misconceptions about the equal sign, meaning that instead of interpreting the equal sign as a symbol for ‘here comes the answer’, they considered it as a symbol reflecting the equality of the expressions on both sides. The tasks with the hanging mobile, in which our main focus was to let students develop strategies related to maintaining the equality in equations and as such to provide them with a basis for solving equations later on, seem to have contributed to their understanding of the equal sign, even in formally notated equations.

Discussion

In this study we investigated the development of students’ algebraic reasoning in an embodied learning environment and the possible relation between the characteristics of the learning environment and the applied algebraic strategies. In the three consecutive episodes in which students worked on problems involving systems of two linear equations, they clearly showed progress in level of reasoning and success rate. At first more than half of the 65 students reasoned without making use of the information in the given equations. Over the teaching sequence, this decreased to about one-fifth of the students. Similarly, whereas in the beginning less than one-fifth of the students showed the highest level of reasoning, in which they combined the information from both given equations, after the lessons more than half of the students attained this level of reasoning. The individual learning progresses confirmed these findings. The reasoning of most students improved over time without any decline. For 14 students no change was found, 15 students showed a fluctuating pattern, and only four students decreased in their level of reasoning. Further investigation of the students’ written work on the assessment tasks revealed that they also improved in their ability to explain their reasoning and their applied strategies to solve these tasks.

Many students appeared to be reticent in writing down their reasoning. In each class, during the teaching sequence, we observed fluctuations regarding students’ willingness to write down their reasoning. This is a possible explanation for the declining or fluctuating reasoning pattern of some of the students. Another explanation concerns the nature of the assessment task of Episode 4. Whereas in the assessment tasks of Episodes 2 and 3 students had to find relationships between unknowns, in the assessment task of Episode 4 they had to identify the values of unknowns. It could be that asking students to identify the values of unknowns (compared to asking them about relationships between unknowns) made it seemingly easier for them to find a correct answer, while at the same time they did not write down their reasoning. Because our categorization of students’ levels of reasoning was based on their written explanations, we had to assign them to level R0 (‘student does not use any of the given equations’) if they did not write anything down. Of the 19 students that showed a fluctuating or declining pattern of reasoning, 11 declined in their level of reasoning from Episode 3 to Episode 4, while 10 of these 11 students answered the assessment task of Episode 4 correctly. This seems to support the latter explanation.

We found some indications for the existence of a relation between the characteristics of the embodied learning environment and the students’ algebraic reasoning. Particular ways of reasoning, uses of strategies and forms of notations could be related to the students’ (physical) experiences of working with this hanging mobile. The influence of these experiences seemed to be present when the problems were posed in different contexts, and students often used similar strategies to solve the problems as when they were working with the hanging mobile. Thus, the acquired strategies appeared to form a base for solving new problems. This came even more to the fore when students used restructuring, isolation and substitution strategies to solve systems of two symbolic linear equations. The hanging mobile seemed to evolve into a model on which students could rely for solving equations at a formal level. This was exemplified by Kees’ reasoning in his solution of the assessment task in Episode 4 (see Figure 6), in which he clearly made use of the model of the hanging mobile to solve a system of two formally notated linear equations.

In line with embodied cognition theory (e.g., Wilson, 2002), we assumed that students’ perceptual-motor experiences with the hanging mobile would be beneficial for their linear equation solving abilities. During the teaching sequence, students could directly perceive how the status of the balance — representing equality in a linear equation — was influenced by their manipulations of the bags on the hanging mobile. This action-perception coupling was expected to ground students’ understanding of equality, a crucial concept in linear equation solving (e.g., Bush & Karp, 2013; Knuth et al., 2005; Li et al., 2008), in the bodily based experiences of maintaining balance. The result of such a possible coupling appeared to be exemplified by students’ reasoning in Episode 3, in which students used the algebraic strategies and provided explanations in terms of actions that could be related to their working on the hanging mobile. However, the design of our study precludes us from truly deciding about the veracity of our assumptions about the working mechanisms governing students’ development of algebraic reasoning in interaction with the physical hanging mobile.

In addition to these findings, it was remarkable that most of our students, when they had to solve linear equations, did not seem to show difficulties that are often reported in other studies. For example, students did not show a lack of relational understanding of the equal sign (e.g., Behr et al., 1980; Carpenter et al., 2003). Students showed this relational understanding in the assessment tasks of Episodes 3 and 4 by correctly interpreting the equal sign as a signal for equality instead of as a ‘to-do’ signal. This is striking, because based on the mathematics curriculum, students only have experience with the equal sign in tasks in the standard form (e.g., a + b = c). Tasks in a non-standard form (e.g., c = a + b or a + b = c + d) that could promote a relational interpretation of the equal sign are scarcely addressed in the curriculum. Obviously, our approach with the hanging mobile, in which the focus was on developing strategies in order to maintaining the equality in equations, helped the students in acquiring a relational understanding of the equal sign.

Furthermore, the students in our study also did not show difficulties with the formal, symbolic way of notating equations (e.g., Koedinger & Nathan, 2004), nor with operations on unknowns (e.g., Filloy & Rojano, 1989; Herscovics & Linchevski, 1994). Being proficient at solving this type of problem means that the students do not only have to understand the given equations, but also have to be able to manipulate and combine them to use this newly gathered information about the unknowns in solving the problems. For students at the primary school age, who have never been taught linear equation solving, this requires significant higher-order thinking. In this way, the findings of our study plainly support the generally agreed ambition (see, e.g., National Council of Teachers of Mathematics [NCTM], 2000) to lay the foundation for higher-order thinking already in primary education.

In interpreting the results of our study it is important to take several limitations into consideration. First of all, the exploratory nature of this study enabled us to explore the development of algebraic reasoning of the students in our study. However, there are some limitations associated with this design, such as the lack of a control group, that imply the results should be interpreted carefully. Additional research with an experimental study is therefore necessary to further evaluate the influence of experiences in an embodied learning environment, such as the hanging mobile, on algebraic reasoning.

A second issue concerns how we measured students’ reasoning. Our classification of students’ level of reasoning was based on written answers and not on think-aloud protocols. This means that we might not have fully captured their reasoning. As such, their level of reasoning may have been underestimated. This is also suggested by the observation that some students were very well able to verbally explain their reasoning during the lessons but did not write their thoughts with the same level of sophistication on the assessment tasks. A further aspect to consider is the repeated assessment of solving linear equations, which could have given students more opportunities to learn how to solve these problems. Therefore, it is important to acknowledge that, in addition to the effect of the experiences with the hanging mobile, the mere use of the assessment tasks could have contributed to students’ progress in their level of reasoning. Moreover, having assessment tasks that directly followed after the teaching activities and that focused on the same content as addressed in the lessons could have influenced the students’ results on the tasks. A delayed assessment might have provided a better view on what the students gained from the lessons.

A next issue of concern is that although our study was carried out in a regular classroom setting, it was the researcher who taught the lessons. This means that one might wonder whether this kind of algebra instruction with concrete apparatus is feasible to be carried out in regular educational practice. In addition one might wonder to what extent primary school classroom teachers are prepared for, and feel confident in, teaching such lessons.

A question that we also did not answer is whether the teaching of linear equation solving by means of the hanging mobile can be implemented in the longer trajectory of teaching algebra. In our study, the topic of linear equation solving was also rather shortly dealt with and consisted only of teaching equations with positive numbers and addition. Additional research is necessary to investigate how the support by the hanging mobile works out for other types of equations including negative numbers or subtraction that cannot be modelled by such a concrete model. As other authors have emphasized (e.g., Fyfe, McNeil, Son, & Goldstone, 2014), a process of concreteness fading might be necessary, beginning with visual representations and fading into abstract symbols.

Notwithstanding the aforementioned limitations, our findings illustrate that fifth-grade students can successfully apply algebraic strategies such as restructuring, isolation and substitution when solving linear equations. Thus, the embodied learning environment in our study seems to have laid a basis for mathematical reasoning in later stages when solving systems of symbolically presented linear equations.

El desarrollo del razonamiento algebraico en educación primaria utilizando una balanza como herramienta de apoyo

La expresión álgebra temprana hace referencia a la introducción del pensamiento algebraico en la educación primaria (Kaput, Carraher, & Blanton, 2008) y su objetivo es constituir una base que permita el acceso de los estudiantes a conceptos algebraicos más avanzados en los cursos siguientes (e.g., Carraher & Schliemann, 2014). El álgebra temprana no consiste simplemente en ‘enseñar álgebra antes’ ni en enseñar álgebra formal a los estudiantes de educación primaria (Carraher, Schliemann, & Schwartz, 2008). Por el contrario, el álgebra se concibe como una línea de pensamiento y de resolución de problemas longitudinal, que comienza en preescolar y continúa en los cursos superiores (e.g., Kaput, 2008). El álgebra temprana implica diversos conceptos importantes como equivalencia y ecuaciones, variable, y razonamiento proporcional (Blanton et al., 2015). Desde muy pequeños, los estudiantes pueden participar en actividades de resolución de problemas relacionadas con estos conceptos, recurriendo a sus conocimientos de procedimientos y habilidades numéricos (Blanton et al., 2007). Además, las experiencias cotidianas de los estudiantes y sus ‘formas de razonamiento intuitivas e informales’ (Stephens et al., 2017, p. 143) son la base para suscitar y desarrollar el pensamiento algebraico necesario para resolver, por ejemplo, ecuaciones lineales básicas. En este artículo, describimos cómo, mediante su participación en actividades de aprendizaje corporizado durante una secuencia de enseñanza de seis lecciones sobre resolución de ecuaciones lineales, los estudiantes de educación primaria desarrollaron estrategias algebraicas contextualizadas que, en último término, les permitieron resolver un sistema de dos ecuaciones lineales con dos incógnitas.

Resolución de ecuaciones lineales

La principal característica de una ecuación es que las expresiones a ambos lados del signo representan el mismo valor. En este sentido, ambos lados de la ecuación son equivalentes, aunque pueden parecer distintos. Esta equivalencia debe mantenerse durante el proceso de resolución de una ecuación. Por tanto, la equivalencia es un concepto clave en la resolución de ecuaciones lineales (e.g., Bush & Karp, 2013; Knuth, Alibali, McNeil, Weinberg, & Stephens, 2005; Li, Ding, Capraro, & Capraro, 2008). Comprender este concepto es uno de los requisitos principales para resolver ecuaciones lineales (Kieran, 1997; Kieran, Pang, Schifter, & Ng, 2016).

En el proceso de resolución de ecuaciones, el objetivo es hallar el valor (o valores) de la incógnita (o incógnitas) de modo que ambos lados de la ecuación sean equivalentes. Este objetivo puede alcanzarse aislando la incógnita. Para ello, los estudiantes deben manipular ambos términos de modo que se mantenga su igualdad. Esta característica suele ponerse de relieve haciendo referencia a la metáfora del ‘equilibrio’ de la ecuación (Ngu & Phan, 2016), que implica realizar transformaciones siguiendo el principio de ‘hacer lo mismo a ambos lados’. Entre otras cosas, se requiere una actividad preparatoria de restructuración de la ecuación dada mediante, por ejemplo, cambiar el orden de los elementos de cada término utilizando las propiedades asociativa y conmutativa, reemplazar unas expresiones por otras equivalentes o intercambiar ambos términos, puesto que la simetría de la igualdad lo permite. A nivel formal, esta restructuración puede requerir la representación de las incógnitas de manera ampliada (e.g., A + A) o abreviada (e.g., 2A). La simplificación de una ecuación para aislar la incógnita puede hacerse, por ejemplo, eliminando los mismos elementos de ambos lados o dividiendo las expresiones en ambos lados. Un método menos específico para resolver ecuaciones es el tanteo-y-comprobación. Consiste en probar distintos valores de la incógnita en la ecuación hasta obtener la respuesta correcta (e.g., Stacey & MacGregor, 1999).

Para resolver un sistema de ecuaciones lineales con varias incógnitas, necesitamos conocer los datos de más de una ecuación para averiguar los valores de las incógnitas. En este caso, el método de aislamiento de las incógnitas puede aplicarse eliminando una de ellas, por ejemplo, restando una ecuación de otra. No obstante, el método más destacado para resolver un sistema de ecuaciones lineales con múltiples incógnitas es el método de sustitución (sustituir una expresión por otra con el mismo valor).

Cuando se aplican estas estrategias, es esencial que los estudiantes tengan una buena comprensión del concepto de equivalencia y de las propiedades de las operaciones. Muchas de las dificultades con las que se encuentran los estudiantes para resolver (sistemas de) ecuaciones lineales están relacionados con la interpretación incorrecta del signo de igual. Los alumnos suelen considerarlo como representación de ‘después va la solución’, o como un signo de ‘suma’ (e.g., Behr, Erlwanger, & Nichols, 1980; Carpenter, Franke, & Levi, 2003) en lugar de como un símbolo que refleja la equivalencia de las expresiones en ambos lados (e.g., Knuth, Stephens, McNeil, & Alibali, 2006). Esta concepción, correcta, del signo igual como símbolo relacional mantiene un vínculo positivo con la competencia para resolver ecuaciones lineales (e.g., Alibali, Knuth, Hattikudur, McNeil, & Stephens, 2007; Knuth et al., 2006; Matthews, Rittle-Johnson, McEldoon, & Taylor, 2012). Otras dificultades conocidas a las que se enfrentan los escolares al resolver ecuaciones lineales están relacionadas con la comprensión de las representaciones formales y simbólicas de las ecuaciones (e.g., Koedinger & Nathan, 2004) y con dificultades para operar con incógnitas durante la resolución de las ecuaciones (e.g., Filloy & Rojano, 1989; Herscovics & Linchevski, 1994).

Enseñar a resolver ecuaciones lineales

Todos los enfoques desarrollados para enseñar a resolver ecuaciones lineales tratan de superar estas dificultades de un modo u otro. En el contexto de la Enseñanza Matemática Realista (RME, por su nombre en inglés; véase, e.g., Van den Heuvel-Panhuizen & Drijvers, 2014), esto significa empezar con situaciones significativas en las que los estudiantes pueden resolver problemas informales similares a las ecuaciones mediante estrategias vinculadas al contexto y después, mediante un proceso de matematización progresiva, acceden a procesos de resolución más formales y estándar. En un estudio de Van Reeuwijk (1995), los estudiantes tenían que calcular el precio de una camiseta y un refresco, si dos camisetas y dos refrescos costaban 44 dólares y una camiseta y tres refrescos costaban 30 dólares. Los estudiantes son más proclives a resolver problemas como este, que tienen sentido para ellos. Cuando un problema tiene sentido para el estudiante o, dicho de otro modo, cuando pueden imaginar qué sucede en ese problema, se les puede abrir su abanico de acciones para resolverlo (Van den Heuvel-Panhuizen & Drijvers, 2014). En este caso, reduciendo el primer conjunto de camisetas y refrescos a la mitad, los estudiantes pueden averiguar cuánto cuesta una camiseta y un refresco, por lo que pueden calcular que dos refrescos cuestan 8 dólares. Las estrategias de aislamiento (por eliminación) y de sustitución desarrolladas para resolver este problema pueden utilizarse más adelante para resolver otros sistemas de ecuaciones lineales. En otras palabras, el contexto significativo de las camisetas y los refrescos puede constituir un modelo para resolver otros problemas.

Además de este modelo contextual, para enseñar a resolver ecuaciones lineales también se utilizan otros modelos matemáticos, como modelos de área, modelos lineales y modelos de balanzas, (Van Amerom, 2002). Estos modelos también ayudan a los estudiantes a comprender qué significa resolver una ecuación y a desarrollar estrategias para hallar los valores de las incógnitas. Entre estos modelos, el modelo de la balanza goza de una larga historia didáctica. Ya lo utilizó Leibniz (1646–1716), que mencionó la relación entre la igualdad en una relación matemática y una balanza con los mismos objetos en ambos lados (Leibniz, 1989).

Una revisión reciente de la literatura sobre el tema (Otten, Van den Heuvel-Panhuizen, & Veldhuis, 2019) reveló que, en la enseñanza de la resolución de ecuaciones lineales, el modelo de la balanza se utiliza con varios aspectos. Puede tratarse de un modelo físico, un dibujo o una balanza virtual en un dispositivo digital. Cada uno de estos tipos de balanzas, que en algunos estudios se utilizan combinados, tiene sus ventajas. Se seleccionan modelos físicos porque la experiencia física que los estudiantes tienen al interactuar con estos dispositivos se considera positiva para el proceso de aprendizaje. En un metaanálisis reciente sobre la eficacia de los materiales manipulativos en la enseñanza matemática reveló efectos entre pequeños y moderados en favor del uso de manipulativos en comparación con la enseñanza basada en el simbolismo abstracto (Carbonneau, Marley, & Selig, 2013). La teoría de la cognición corporizada (e.g., Pouw, Van Gog, & Paas, 2014) ofrece una perspectiva teórica sobre los mecanismos que subyacen en el aprendizaje con manipulativos. Esta teoría afirma que las experiencias corporales pueden contribuir de manera positiva al proceso cognitivo de aprendizaje (e.g., Wilson, 2002). La cognición no se forma únicamente por y en nuestro cerebro, sino también mediante las experiencias sensoriales y motoras que experimentamos cuando nuestro cuerpo interactúa con el mundo (e.g., Gallese & Lakoff, 2005; Wilson, 2002). Por tanto, los entornos de aprendizaje corporizado (denominación abreviada de los entornos de aprendizaje basados en la teoría de la cognición corporizada) se consideran esenciales en el aprendizaje de las matemáticas (Abrahamson, 2017; Lakoff & Núñez, 2000; Núñez, Edwards, & Matos, 1999). Mediante la combinación de acción y percepción, las experiencias sensoriales y motoras constituyen la base para el surgimiento de conceptos matemáticos y del razonamiento matemático, mediados por metáforas conceptuales (Lakoff & Johnson, 1980) y redescripción representacional (Karmiloff-Smith, 1992). Así pues, por ejemplo, mediante las experiencias físicas con una balanza real, los estudiantes pueden reforzar su concepción de la igualdad y sus experiencias físicas sobre cómo mantener el equilibrio y pueden dirigir ambas hacia una comprensión más abstracta, necesaria para resolver ecuaciones lineales en un nivel formal.

Diversas investigaciones en las que se utilizó el modelo de la balanza para enseñar a resolver ecuaciones lineales han demostrado que este modelo puede ayudar a los estudiantes. No obstante, no se han obtenido resultados positivos para todos los tipos de modelos de equilibrio. Los más positivos han sido los obtenidos con modelos físicos (e.g., Perry, Berch, & Singleton, 1995; Warren & Cooper, 2005) y virtuales (Figueira-Sampaio, Santos, & Carrijo, 2009; Suh & Moyer, 2007). Por lo que respecta a modelos dibujados, algunos estudios obtuvieron resultados positivos (e.g., Araya et al., 2010; Cooper & Warren, 2008), mientras que otros obtuvieron resultados tanto positivos como negativos (e.g., Linchevski & Herscovics, 1996; Vlassis, 2002), o incluso solo negativos (e.g., Ngu & Phan, 2016).

Una característica de los modelos de balanza físicos es que son dinámicos, es decir, que los estudiantes pueden utilizarlos para operar y observar los resultados de sus acciones en tiempo real. Esto les puede ayudar a desarrollar estrategias para mantener la balanza en equilibrio. Sin embargo, la mayoría de los estudios en los que se utilizó un modelo físico de balanza (e.g., Perry et al., 1995) únicamente revelan el tipo de ecuaciones que los estudiantes aprenden a resolver y apenas arrojan datos sobre el desarrollo del razonamiento algebraico que utilizan para resolverlas. Lo mismo ocurre con las estrategias algebraicas básicas utilizadas en sus actividades con el modelo físico. El objetivo de este estudio es contribuir a incrementar el conocimiento actual sobre la aportación de un entorno de aprendizaje corporizado con un modelo de balanza física al razonamiento de los estudiantes.

El presente estudio

En este estudio se utilizó una secuencia de enseñanza de seis lecciones sobre resolución de ecuaciones lineales, basadas en la teoría de la cognición corporizada y en el principio de la enseñanza matemática realista de empezar con un contexto significativo que puede evolucionar a un modelo que, en último término, permita resolver un sistema de dos ecuaciones lineales con dos incógnitas presentadas simbólicamente. En esta secuencia de enseñanza se suscita el razonamiento algebraico mediante unas actividades en las que se ofrecieron a los estudiantes experiencias corporizadas mediante un móvil colgante: un modelo de balanza que, en cada lado, dispone de una serie de bolas que cuelgan de una cadena y que representan una ecuación con incógnitas. Se utilizaron bolas de distintos colores, cada una con un peso diferente (e.g., blanco = 50 gr, rojo = 100 gr, negro = 150 gr). Los estudiantes desconocían los distintos pesos de las bolas y tenían que hallar maneras de mantener el equilibrio de la balanza manipulando las bolas de distintos colores.

Proponíamos que, cuando los estudiantes interactuasen con la balanza tratando de mantener su equilibrio, podrían reactivarse las experiencias generales de equilibrio de la vida cotidiana (Gibbs, 2006) y se podrían establecer vínculos con la experiencia de mantener la balanza en equilibrio como representación de la igualdad en una ecuación lineal. De este modo, el conocimiento del concepto de equivalencia por parte de los estudiantes podría basarse en las experiencias corporizadas de mantener el equilibrio de la balanza, en línea también con la afirmación de Piaget de que los niños ‘solo son capaces de “abstraer” la idea de una relación como la igualdad sobre la base de una acción de igualación’ (Piaget & Inhelder, 1967, p. 43; traducción propia). Las posibles manipulaciones físicas que mantienen el equilibrio de la balanza podrían actuar a modo de representación metafórica (Lakoff & Johnson, 1980; Núñez et al., 1999) de las estrategias algebraicas que pueden utilizarse para mantener la igualdad en las ecuaciones. En particular, las manipulaciones de las bolas por los estudiantes pueden provocar el desequilibrio o el equilibrio de la balanza. Por ejemplo, los estudiantes pueden quitar bolas similares de ambos lados de la balanza. Al hacerlo, notan que los pesos de las bolas que tienen en sus manos son similares y, al mismo tiempo, perciben que el brazo de la balanza permanece en equilibrio. Por tanto, los estudiantes experimentan físicamente el principio de ‘hacer lo mismo en ambos lados’, que es una estrategia importante para resolver ecuaciones (e.g., Arcavi, Drijvers, & Stacey, 2016). Cuando trabajan con la balanza, los estudiantes perciben directamente el efecto de sus acciones — como quitar bolas — en el estado de la balanza. De acuerdo con la teoría de la cognición corporizada, nuestra hipótesis es que estas experiencias motoras y sensoriales podrían fomentar la fundamentación del concepto de igualdad en la experiencia corporizada de mantener el equilibrio.

Mediante sus acciones para mantener el equilibrio de la balanza, los estudiantes pueden aplicar de manera intuitiva estrategias algebraicas informales vinculadas al contexto que subyacen a las estrategias convencionales para resolver ecuaciones, como cambiar el orden de las bolas (restructuración), quitar bolas en ambos lados de la balanza para aislar las del mismo color (simplificación/aislamiento) y sustituir unas bolas por otras de otro color (sustitución). Nuestra hipótesis es que, mediante la exploración de las acciones que mantienen el equilibrio de la balanza, en combinación con algunas tareas complicadas, los estudiantes podrían encontrar, de manera más o menos espontánea, estrategias que sean la base para las estrategias algebraicas clave necesarias para resolver ecuaciones. Este enfoque, en el que los estudiantes desempeñan un papel esencial en el aprendizaje del razonamiento algebraico, también refleja los principios didácticos de la enseñanza matemática realista, concretamente que, en lugar de que el profesor transfiera las estrategias a los estudiantes, estos sean participantes activos en su desarrollo de dichas estrategias algebraicas.

En este estudio, nuestro objetivo era probar esta secuencia de enseñanza e investigar cómo se desarrollan el razonamiento y la comprensión algebraicos de los estudiantes y si ciertas características de su razonamiento y comprensión están vinculadas a lo que se les ofrece en la secuencia de enseñanza. En concreto, planteamos las siguientes preguntas de investigación:

1. ¿Cómo se desarrolla el razonamiento algebraico de los estudiantes de quinto curso para la resolución de ecuaciones lineales en un entorno de aprendizaje corporizado?

2. ¿Qué relación existe entre las experiencias de los estudiantes en el entorno de aprendizaje y su uso de estrategias algebraicas?

Durante la secuencia de enseñanza, esperábamos observar una mejora en el razonamiento algebraico de los estudiantes para resolver ecuaciones lineales. Además, esperábamos que sus experiencias motoras y sensoriales con el modelo móvil resultasen beneficiosas para la resolución de ecuaciones en el contexto del modelo, en nuevos contextos informales y también en el contexto formal. Por tanto, esperábamos observar referencias a (las experiencias con) la balanza al analizar el razonamiento de los estudiantes.

Método

Participantes

Para responder a las preguntas de investigación llevamos a cabo un estudio con 69 estudiantes de quinto curso en tres escuelas holandesas. Dos de ellas, una pública y una católica, estaban situadas en zonas urbanas, mientras que la tercera era una escuela pública situada en una zona suburbana. El estudio fue aprobado por el Comité de Ética de la Facultad de Ciencias Sociales y Conductuales de la Universidad de Utrecht. Se solicitó el consentimiento informado de los padres de los participantes y se obtuvo permiso para utilizar los datos de todos los estudiantes excepto tres. Estos tres estudiantes fueron excluidos de los análisis. Un cuarto estudiante fue excluido porque estuvo ausente de la mayor parte de las lecciones. Por lo tanto, el número final de participantes fue de 65 escolares, 27 niños (42%) y 38 niñas (58%), con edades entre 9 y 11 años (M = 10.02, DT = 0.45). Los participantes no habían recibido ningún tipo de enseñanza previa sobre la resolución de ecuaciones ni sobre cualquier otro tema relacionado con el álgebra, como indica el currículum de matemáticas en Holanda, en el que la enseñanza del álgebra comienza en el primer curso de secundaria.

Materiales

Secuencia de enseñanza

La secuencia de enseñanza (véase Figura 1) consistió en seis lecciones, agrupadas en cuatro episodios, cada uno de ellos con su propio enfoque y contenido. El objetivo de cada episodio era desarrollar estrategias algebraicas relacionadas con la resolución de ecuaciones lineales.

Figura 1. La secuencia de enseñanza y su contenido.

En el episodio 1, los estudiantes adquirían experiencias físicas con un modelo móvil colgante a modo de balanza. El brazo oscilante de la balanza podía estar equilibrado o desequilibrado, permitiendo a los estudiantes observar en tiempo real el efecto de sus acciones durante la manipulación de las bolas de la balanza. Mientras los estudiantes manipulaban la balanza, la profesora planteaba preguntas como, por ejemplo: ‘¿Podrías explicar por qué el brazo de la balanza está recto?’. ‘¿Podrías explicar por qué el brazo de la balanza sigue estando recto después de lo que acabas de hacer?’ o ‘¿Es posible quitar alguna bola de la balanza de modo que siga estando equilibrada?’ Durante la consiguiente discusión en grupo, colocamos una balanza delante de la clase. Se pidió a los estudiantes que enumerasen todas las acciones posibles que podrían realizar manteniendo la balanza en equilibrio. Estas acciones se llevaron a cabo en la balanza y la profesora anotó las posibilidades en la pizarra, utilizando las mismas palabras de los estudiantes (e.g., ‘podrían cambiarse bolas de un color por bolas de otro color’ en lugar de ‘sustitución’). Como los estudiantes habían trabajado con una balanza en el primer episodio, razonaban sobre una ecuación.

En los episodios siguientes, fue necesario combinar la información de dos ecuaciones para descubrir relaciones entre las incógnitas para resolver el problema, de modo que los estudiantes razonaban sobre un sistema de ecuaciones. En el episodio 2, todavía se plantearon los problemas en el contexto de la balanza, tanto físicamente como sobre el papel. La profesora comenzó preguntando si sería posible combinar la información de las dos balanzas que estaban colocadas delante de la clase para crear una nueva balanza. Tras recopilar las propuestas de los estudiantes, la profesora invitó a uno de ellos a manipular las bolas en las dos balanzas para identificar una nueva relación entre las incógnitas y mostrarla en la tercera balanza. A continuación, los estudiantes trabajaron sobre el papel con tareas en las que debían combinar los datos de las dos balanzas iniciales.

En el episodio 3, había que combinar la información de las dos ecuaciones para descubrir relaciones entre las incógnitas en nuevos contextos como el juego de la cuerda. En este episodio, la profesora comenzó con una discusión conjunta sobre las semejanzas entre el nuevo contexto de la cuerda y el contexto ya conocido de la balanza, concretamente que en ambos contextos se trata de mantener la igualdad. Después, se revisaron todas las acciones posibles para mantener el equilibrio en la balanza, antes de que los estudiantes empezaran a resolver problemas en el nuevo contexto del juego de la cuerda. Al mismo tiempo, en este episodio se motivó gradualmente a los estudiantes para que utilizasen notaciones más simbólicas, como letras para indicar la fuerza de los animales que participan en el juego de la cuerda. Para ello, se pidió a los estudiantes que pensasen en maneras alternativas de expresar sus explicaciones, como, por ejemplo, evitar el largo proceso de dibujar los animales o de escribir la totalidad del proceso de razonamiento.

En el último episodio, el episodio 4, en lugar de descubrir las relaciones entre las incógnitas, los estudiantes tenían que hallar los valores de estas en un sistema de dos ecuaciones lineales con incógnitas expresadas simbólicamente. A modo de introducción, la profesora explicó de nuevo la analogía entre el modelo de la balanza y estas nuevas ecuaciones expresadas simbólicamente. Además, comentó el significado de las notaciones simbólicas, dirigiendo la discusión, por ejemplo, hacia discusiones sobre si ‘2N’ es lo mismo que ‘N + N’ o si ‘1N’ podría ser una alternativa de expresar ‘N’.

Durante la secuencia de enseñanza, los estudiantes encontraron muchos tipos de ecuaciones en los que aparecían distintos tipos de cantidades. Por ejemplo, durante las actividades con la balanza colgante (episodios 1 y 2), trabajaban con pesos (e.g., tres bolas blancas pesan lo mismo que una negra). En el juego de la cuerda (episodio 3), trabajaron con la igualdad de fuerzas (e.g., una oveja es tan fuerte como tres gallinas). En el episodio 4, trabajaron con objetos y precios (una manzana y un plátano cuestan en total ocho euros) y acabaron con ecuaciones expresadas formalmente con un signo de igual y con incógnitas representadas por letras (M + 3L = 25 y M = 2L) que no estaban relacionadas con ningún tipo de cantidad dada, como el peso, la fuerza o el coste por objeto.

Evaluación el razonamiento algebraico

Se evaluó el nivel del razonamiento algebraico de los estudiantes vinculado a la resolución de ecuaciones lineales mediante tareas escritas de evaluación realizadas al final de cada sesión (el Apéndice A, Figuras A1–A3, muestra ejemplos de las tareas de evaluación de los episodios 2–4). Cada tarea de evaluación reflejaba el objetivo de la lección correspondiente. La tarea de evaluación del episodio 2 incluía dos balanzas en las que había círculos, rectángulos y estrellas, a modo de representación informal de las ecuaciones formales 3X = Y + 5Z y Y = X + Z. Tomando estas balanzas como base, los estudiantes tenían que determinar si otras dos balanzas (X = 3Z y 4Z = Y) estaban equilibradas. En la tarea de evaluación del episodio 3, se utilizaron las mismas ecuaciones, pero con fresas, plátanos y peras, y con un signo de igual en lugar de la balanza. Por último, en el episodio 4, los estudiantes tenían que resolver un sistema de dos ecuaciones representadas simbólicamente. En esta tarea de evaluación, los estudiantes tenían que descubrir los valores de las incógnitas M y L utilizando las ecuaciones M + 3L = 25 y 2M = 4L.

En todas las tareas, además de dar la respuesta al problema, los estudiantes tenían que explicar su razonamiento. Las respuestas se puntuaron como incorrectas (0) o correctas (1) y se utilizó esta puntuación dicotómica para calcular la tasa de éxito, es decir, el porcentaje de respuestas correctas por tarea de evaluación. Las explicaciones de los estudiantes se categorizaron en función del nivel de razonamiento mostrado mediante un sistema de codificación (véase la sección Análisis de datos).

Procedimiento

La primera autora del artículo impartió las lecciones de 50 minutos durante seis semanas consecutivas, con la ayuda de un profesor ayudante durante las dos lecciones del primer episodio. El episodio 1 se llevó a cabo en un aula diferente de la ordinaria, en la que se colocaron cinco balanzas. Durante este episodio, los estudiantes trabajaron en pequeños grupos de dos o tres estudiantes. Los episodios siguientes tuvieron lugar en el aula ordinaria de los estudiantes. Durante cada episodio había al menos una balanza en el aula, incluso cuando no se utilizaba para la enseñanza. Después del primer episodio, los estudiantes trabajaron de manera individual, en parejas o en pequeños grupos. El trabajo individual o en grupo se alternó con discusiones del conjunto de la clase. Entre lecciones, los estudiantes siguieron su programación ordinaria.

En el primer episodio, en una clase, se grabó en video a dos parejas de estudiantes, de modo que se pudiesen seguir sus manipulaciones con la balanza y su razonamiento con mayor precisión. Se grabó a estos estudiantes particulares porque se contaba con el permiso de los padres para ello. Durante el resto de los episodios, la cámara se colocó al fondo de la clase para ofrecer un panorama global de las actividades de las lecciones. En las otras dos clases, se grabaron dos parejas de estudiantes durante el primer episodio, y también se siguió grabando su trabajo y sus conversaciones en los episodios siguientes. De este modo, pudimos realizar un seguimiento del razonamiento de estos estudiantes en el tiempo. Además de centrarnos en estas dos parejas de estudiantes, a partir del episodio 2, se colocó una cámara adicional al fondo de las clases para ofrecer también un panorama global de las actividades en las dos clases.

Análisis de datos

Los datos analizados eran las respuestas de los estudiantes a los problemas presentados durante las lecciones y en las pruebas de evaluación, así como las grabaciones de audio y vídeo. Para analizar el desarrollo del razonamiento algebraico de los estudiantes en el tiempo (Pregunta de investigación 1), nos centramos en los tres episodios consecutivos en los que los estudiantes resolvieron sistemas de ecuaciones lineales (episodios 2–4). En cada episodio, se analizó la tarea de evaluación que los estudiantes realizaron al final del episodio (véase algunos ejemplos en Apéndice A, Figuras A1–A3).

Para calcular la tasa de éxito de cada tarea de evaluación, se puntuaron las respuestas de los estudiantes como correctas cuando ambos problemas eran resueltos correctamente. La tarea correspondiente al episodio 4 se consideró correcta cuando el valor de ambas incógnitas era correcto.

Para categorizar las explicaciones de los estudiantes en las tareas de evaluación, se aplicó un sistema de codificación aplicable a todas las tareas. El desarrollo de este sistema de codificación se hizo mediante un proceso iterativo, inspirado en el método de comparación constante (Glaser, 1965). Comenzamos con un sistema de codificación basado en el trabajo de un par de estudiantes y este sistema se tomó como punto de partida para codificar el resto de los datos. Cuando se hallaron ejemplos de trabajo de estudiantes que no encajaban en el sistema utilizado, procedimos a adaptar el sistema. Tras diversas rondas de análisis detallado, se estableció el sistema de codificación definitivo por consenso entre los investigadores. A continuación, se realizó una ronda final de codificación en la que se recodificaron los datos en función del sistema final.

En cada tarea de evaluación de los episodios 2 a 4, los estudiantes tenían que resolver el problema mediante un razonamiento basado en un sistema de dos ecuaciones dado. En el sistema de codificación definitivo, distinguimos entre estudiantes que no utilizaron ninguna de las ecuaciones en la descripción de su razonamiento (Nivel R0), estudiantes cuyo razonamiento hacía referencia solamente a una de las dos ecuaciones (Nivel R1) y estudiantes cuyo razonamiento aludía a ambas ecuaciones, combinando la información de ambas (Nivel R2). En los niveles R1 y R2, distinguimos además entre (1) estudiantes que no explicitaban cómo llegaban al resultado o qué estrategias utilizaron y (2) estudiantes que sí proporcionaban esta información. El sistema de codificación, con ejemplos de respuestas de estudiantes a cada tarea de evaluación y de cada nivel de razonamiento, se muestra en el Apéndice B.

Además, en cada episodio se evaluó la relación entre el nivel de razonamiento del estudiante y su tasa de éxito mediante un test de independencia chi cuadrado.

Para analizar la posible relación entre las potencialidades del aprendizaje corporizado y el desarrollo del razonamiento algebraico de los estudiantes (Pregunta de investigación 2), examinamos las estrategias algebraicas mostradas en cada episodio, analizando las tareas escritas de los estudiantes y las grabaciones de audio y video y buscando aquellos eventos en los que los estudiantes hicieron uso de estrategias algebraicas para resolver los problemas en la clase. De este modo, después pudimos relacionar el uso de estrategias por parte de los estudiantes con lo sucedido durante la lección en ese episodio concreto.

Resultados

Desarrollo del razonamiento algebraico de los estudiantes en un entorno de aprendizaje corporizado

En el transcurso de la secuencia de enseñanza, los estudiantes daban con más frecuencia respuestas correctas, como muestra el incremento de las tasas de éxito de las respectivas tareas de evaluación, desde el 44% en el episodio 2 al 57% en el episodio 3 y el 77% en el episodio 4. Además, el nivel de razonamiento algebraico de los estudiantes se incrementó con el tiempo, como muestra la Figura 2. El porcentaje de estudiantes cuyo razonamiento no hacía uso de las ecuaciones (Nivel R0) decreció, desde el 57% en el episodio 2 al 20% en el episodio 4. Los estudiantes que mostraron este tipo de razonamiento daban explicaciones como, por ejemplo, ‘sabía la respuesta’ y ofrecían una descripción general como ‘me fijé en el ejemplo’, sin indicar explícitamente qué datos utilizó para llegar a su respuesta, o no escribieron nada. El porcentaje de estudiantes que expresó un razonamiento que hacía uso de una sola ecuación (R1) se mantuvo más o menos estable, entre 23% y 28%. La respuesta de Julia en las tareas de evaluación del episodio 2 (véase Apéndice A, Figura A1) ilustra el tipo de razonamiento categorizado como Nivel R1. Julia asignó valores a las incógnitas teniendo en cuenta solo la segunda ecuación, haciendo caso omiso de la información ofrecida en la primera. Por último, el porcentaje de estudiantes que demostraron un razonamiento con alusiones a las dos ecuaciones (Nivel R2) se incrementó con el tiempo, del 17% en el episodio 2 al 52% en el episodio 4. El razonamiento de Julia en las tareas de evaluación de los episodios 3 y 4 (véase Apéndice A, Figuras A2 y A3) ilustra este nivel de razonamiento. Por ejemplo, en la tarea de evaluación del episodio 4 (véase Apéndice A, Figura A3), Julia transformó primero la ecuación 2M = 4L en M = 2L. A continuación, utilizó esta información para sustituir la incógnita M de la otra ecuación por 2L. De este modo, combinó la información de ambas ecuaciones para encontrar la respuesta, un proceso característico del nivel de razonamiento R2.

Figura 2. Porcentajes de estudiantes en cada nivel de razonamiento en los tres episodios (N_{Episodio 2} = 63; N_{Episodio 3} = 65; N_{Episodio 4} = 61).

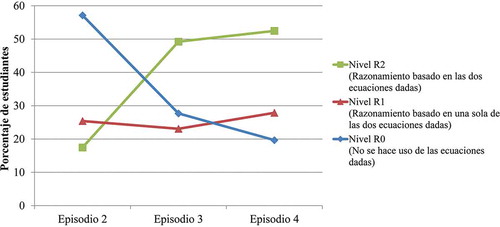
La relación entre el nivel de razonamiento de los estudiantes y su índice de respuestas correctas es diferente en los distintos episodios En el episodio 2 (χ² (2, n = 63) = 2.37, p = .306) y el episodio 3 (χ² (2, n = 65) = 5.97, p = .051), no había relación entre la obtención de una respuesta correcta y el nivel de razonamiento del estudiante, mientras que en el episodio 4 (χ² (2, n = 61) = 8.70 p = .013), se observó mayor frecuencia de respuestas correctas con un nivel elevado de razonamiento y de respuestas incorrectas con un nivel bajo de razonamiento.

También se analizó el desarrollo del nivel de razonamiento para cada estudiante de manera individual. Una estudiante quedó excluida de este análisis puesto que estuvo ausente en dos de las tres tareas de evaluación. En total, 31 estudiantes (48%) mostraron un patrón de razonamiento que mejoró al menos un nivel en el transcurso de la secuencia de enseñanza y no tuvo ningún descenso de nivel. Para cuatro estudiantes (6%), el nivel de razonamiento decreció. Catorce estudiantes (22%) mostraron el mismo nivel de razonamiento durante los tres episodios. Por último, los 15 estudiantes restantes (24%) mostraron un nivel de razonamiento variable, puesto que se incrementó y descendió durante la secuencia de enseñanza.

También observamos un incremento en el número de estudiantes que eran capaces de escribir cómo obtenían la respuesta y/o describir las estrategias que habían utilizado para resolver los problemas. Este fue el caso, en especial, de los estudiantes del nivel R2. Mientras que en el episodio 2, el 16% de los 63 estudiantes con nivel R2 describieron su razonamiento, este porcentaje ascendía al 42% entre los 61 estudiantes que participaron en el episodio 4. Para los estudiantes clasificados en el nivel R1, estos porcentajes oscilaron entre el 17% en el episodio 2 y el 12% en el episodio 4.

Relación entre las experiencias de los estudiantes en el entorno de aprendizaje y su uso de estrategias algebraicas

Episodio 1: experiencias físicas con la balanza

En el primer episodio, todos los estudiantes comenzaron con el mismo modelo, una balanza en equilibrio (véase Figura 1, episodio 1). No se les facilitó información sobre el tipo de relación entre las bolas. En la primera tarea, se les pidió que hiciesen cambios en la balanza de manera que fuese diferente del inicial pero siguiera manteniéndose en equilibrio, utilizando las mismas bolas. La reacción de los estudiantes fue probar distintas estrategias de reestructuración. Por ejemplo, Eva comentó a su compañero Jailey:

Table

Eva: Podemos hacer exactamente lo mismo, pero en el otro lado. Estas	[1]
[indica las bolas de la izquierda] las ponemos en el otro lado y estas [indica	[2]
las de la derecha] también todas al otro lado. O sea, ponemos todas estas bolas allí y	[3]
todas esas bolas también en el otro lado. Así, será diferente, pero seguirá igual	[4]
[risas].	[5]

Iris y Zara mostraron otra estrategia de reestructuración. Estas alumnas cambiaron el orden de las bolas en el brazo derecho de la balanza, agrupándolas por colores. Kees y Julia también reestructuraron la balanza, pero en lugar de cambiar todas las bolas de un lado a otro o agruparlas por colores, movieron tres bolas blancas al lado izquierdo de la balanza y, a cambio, llevaron una negra al lado derecho. Las diversas estrategias de reestructuración identificadas por las tres parejas de estudiantes en su primer encuentro con la balanza se corresponden con tres estrategias algebraicas importantes. La estrategia de Eva y Jailey de intercambiar todas las bolas de la balanza de un lado al otro se corresponde con la propiedad de simetría de las ecuaciones (a = b ≤> b = a). La estrategia de Iris y Zara, que cambiaron el orden de las bolas en un brazo de la balanza, refleja la ley conmutativa de la suma. Kees y Julia descubrieron la relación entre las bolas negras y las blancas y aplicaron la estrategia de sustitución en su reestructuración de la composición de la balanza. Este último tipo de reestructuración fue utilizado por la mayoría de los grupos de estudiantes en esta tarea.

Tras una breve discusión en grupo sobre las composiciones resultantes en las diversas balanzas después de las transformaciones, los estudiantes tenían que identificar todo lo que pudiera hacerse manteniendo la balanza en equilibrio, pero esta vez también podían añadir y quitar bolas. Esta conversación entre Kees y Julia ilustra el surgimiento de su uso y comprensión de la estrategia de aislamiento, retirando primero las incógnitas idénticas de ambos lados de la ecuación (líneas 6–7) y después retirando incógnitas distintas de ambos lados en función de su relación de equivalencia (líneas 9–10). Por otro lado, en la segunda parte de la interacción, durante la discusión con la profesora (T), se ejemplifica su uso de la estrategia de sustitución, que describen verbalmente (líneas 13–15) e ilustran sustituyendo físicamente las bolas en la balanza (líneas 24–5).

Table

Kees: Estas dos [señala las dos bolas rojas del lado izquierdo] son	[6]
lo mismo que estas dos [señala las dos bolas rojas del lado derecho]. Pesan lo mismo …	[7]
Julia: … entonces estas dos negras deben ser lo mismo que 1, 2, 3, 4, 5 …	[8]
6 [bolas blancas] [cuenta las bolas blancas del lado derecho de la balanza].	[9]
O sea, una [negra] equivale a tres [blancas]	[10]
Kees: ¡Sí!	[11]

Un poco después, los estudiantes habían creado una balanza equilibrada con dos bolas negras en el lado izquierdo y dos bolas blancas y dos rojas en el lado derecho.

Table

T: ¿Me podríais decir por qué la balanza está equilibrada?	[12]
Kees: Porque esta bola [señala una bola roja] cuenta como dos blancas [una	[13]
relación que habían descubierto antes]. Y tres blancas equivalen a una negra.	[14]
O sea que una roja y una blanca deben ser lo mismo que una negra.	[15]
T: [mira a Julia] ¿Estás de acuerdo?	[16]
Julia: ¡Sí!	[17]
T: O sea, estás diciendo que si sustituyera esta [señala una bola roja] por dos	[18]
blancas …	[19]
Kees: … ¡es exactamente lo mismo!	[20]
T: ¿Sí? ¿Estás seguro?	[21]
Kees: [asiente]	[22]
T: ¡Vamos a probar!	[23]
Kees: [sustituye una bola roja por dos blancas y observa cómo la balanza se	[24]
reequilibra de nuevo, véase la Figura 3] ¡Mira!	[25]

Figura 3. Kees y Julia sustituyen una bola roja por dos blancas y ven que la balanza recobra el equilibrio (Episodio 1).

En estas actividades, mantener el equilibrio de la balanza representa mantener la igualdad de una ecuación. Las interacciones ilustran claramente que los estudiantes aplicaron distintas estrategias algebraicas, con las que obtuvieron experiencias motoras y sensoriales. Al transformar la balanza cambiando todas las bolas de un lado al otro, los estudiantes pueden experimentar físicamente que ambos lados de la ecuación son intercambiables y que cambiar el orden de las bolas de un lado no altera el equilibrio. Además, quitando bolas iguales de ambos lados, los estudiantes pueden experimentar físicamente la posibilidad de simplificar elementos idénticos en ambos lados, una estrategia que puede utilizarse para aislar incógnitas específicas. La tercera estrategia, la de sustitución, permitió a los estudiantes simplificar la composición de la balanza, acercándoles a identificar todas las relaciones de equivalencia entre las bolas. Mediante la comprobación de los resultados en tiempo real gracias al movimiento del brazo de la balanza, los estudiantes podían verificar sus operaciones constantemente y ajustar su razonamiento si era necesario. Por ejemplo, Kees y Julia mostraron este comportamiento cuando cambiaron la bola roja por dos blancas (líneas 24–25).

Después del trabajo con la balanza en grupos reducidos, los estudiantes compartieron sus experiencias en una discusión general de la clase. Durante estas discusiones, se hizo evidente que la mayoría de los grupos había utilizado estrategias similares para mantener el equilibrio.

Episodio 2: combinación de la información obtenida en dos balanzas

A continuación, los estudiantes tenían que resolver una tarea en la que era necesario combinar la información de dos balanzas, con el objetivo de avanzar en el desarrollo de sus estrategias algebraicas, en particular, la estrategia de sustitución. La profesora presentó la tarea colocando tres balanzas ante la clase (véase Figura 4).

Figura 4. Tres balanzas colocadas ante la clase (Episodio 2).

En una de las clases, Florien alzó la mano cuando la profesora preguntó si sería posible combinar las dos balanzas (A y B) para formar la tercera (C).

Table

Florien: Si duplicas la bola roja,		[26]
se convierte en una amarilla [señala la balanza A].		[27]
Y si duplicas las bolas azules, tendrás cuatro bolas azules.		[28]
Así sabes que cuatro bolas azules son igual que una amarilla.		[29]

La estrategia de Florien era una de las estrategias que surgieron en el resto de las clases. En su caso, preparó la estrategia de sustitución modificando la primera ecuación (A), duplicando sus componentes. De este modo consiguió sustituir un lado completo de la ecuación (dos bolas rojas), haciendo uso de la información ofrecida por la segunda ecuación (B). Tras explicar su estrategia al resto de la clase, lo demostró utilizando las balanzas que había en la clase. A continuación surgió un segundo ejemplo de sustitución en el que, sobre la base de la información disponible en la primera balanza (A), los estudiantes sustituyeron una bola roja de la segunda ecuación (B) por dos azules. En este caso, en lugar de sustituir todo el lado de la ecuación de golpe, se sustituyó una incógnita (un elemento) de la ecuación por otra incógnita. La mayoría de los estudiantes utilizó esta estrategia. Por último, en lugar de sustituir unas incógnitas por otras, diversos estudiantes sustituyeron incógnitas por valores, como en el caso de Mats. Mats asignó el valor 1 a cada incógnita azul, el valor 2 a las rojas y el valor 4 a las incógnitas amarillas, con lo que obtuvo la misma suma en ambos lados de cada ecuación. Aunque no explicó cómo había llegado a esos valores, su elección de los valores mostró que tuvo en cuenta todas las ecuaciones.

Episodio 3: un nuevo context

En este episodio, los estudiantes se enfrentaron a problemas bastante distintos de los planteados en las balanzas, pero con los que seguían existiendo ciertas semejanzas. Dos grupos de animales participaban en el juego de la cuerda y la pregunta era qué grupo iba a ganar (véase Figura 5). También en este caso, la atención se centraba en la igualdad de los dos lados y en averiguar qué grupo es más fuerte, aplicando todo tipo de transformaciones al tiempo que se mantenía el equilibrio.

Figura 5. El problema del juego de la cuerda (Episodio 3).

Milan explicó al resto de la clase su estrategia para resolver el problema. En primer lugar, combinó ambas ecuaciones sumándolas, para crear una ecuación nueva (línea 30). A continuación, aplicó estrategias de aislamiento para resolver la ecuación, retirando primero un caballo de ambos lados (líneas 30–31), después una oveja de ambos lados (líneas 31–32) y después eliminando distintas incógnitas dividiendo ambos lados de la ecuación por dos (línea 33).

Table

Milan: He sumado la línea inferior a la superior. Después he podido quitar los dos	[30]
caballos. Entonces quedaban seis gallinas y una oveja en el lado derecho. Así que	[31]
podía quitar una oveja de cada [lado]. Entonces nos quedan seis [gallinas] y dos	[32]
ovejas. Si dividimos, quedan tres [gallinas].	[33]

Julia utilizó una estrategia distinta para resolver este problema. Primero convirtió el problema en dos ecuaciones con letras y escribió O + O + O | G + G + G + G + G + C y C | O + G. Entonces, sustituyó la C de la primera ecuación por una G y una O, con lo que obtuvo O + O + O | G + G + G + G + G + G + O. Entonces, para aislar las gallinas, tachó una O de ambos lados y por último tachó una O del lado izquierdo y tres G del derecho, quedando O | G + G + G. Julia reescribió esto como ‘1O = GGG3’. La tercera estrategia que algunos estudiantes utilizaron para resolver el problema fue asignar valores a las incógnitas, estrategia que ya fue descrita en el episodio 2.

En este episodio, los estudiantes se enfrentaron a problemas relacionados con las ecuaciones en un contexto nuevo y, una vez más, surgieron distintas estrategias para combinar la información de ambas ecuaciones. Milan (líneas 30–33), por ejemplo, sumó ambas ecuaciones para crear una ecuación nueva con algunas incógnitas idénticas en ambos lados que podía eliminar, para aislar una incógnita en una ecuación y expresarla en otra. No obstante, Milan fue uno de los pocos estudiantes que utilizó esta manera inteligente de combinar ambas ecuaciones para crear una nueva. La mayoría de sus compañeros utilizó la estrategia de sustitución para resolver la tarea. Esta estrategia también fue utilizada con frecuencia al trabajar con las balanzas. En el episodio 3, por ejemplo, esta fue la estrategia utilizada por Julia, que convirtió un tipo de incógnita (el caballo) en los otros dos tipos (la oveja y la gallina). También utilizó este proceso de sustitución de un tipo de incógnita por otros tipos en su trabajo con la balanza del episodio 1 (líneas 9–10).

Las estrategias utilizadas por los estudiantes en este episodio, para resolver el nuevo tipo de problemas relacionados con las ecuaciones, son equivalentes a las estrategias que desarrollaron cuando trabajaban con las balanzas. Al explicar sus respuestas, algunos estudiantes hacían referencias explícitas al trabajo con las balanzas, por ejemplo, utilizando expresiones como ‘el caballo podría considerarse como una bola verde’. En una de las clases, cuando la profesora se despistó un momento, los estudiantes recurrieron a las bolas de colores de la balanza, que no estaban siendo utilizadas entonces, para representar el contexto del juego de la cuerda sobre la mesa. Además, los estudiantes explicaron con frecuencia sus estrategias en términos de acciones, como ‘sustituyo el caballo por una oveja y una gallina y luego quito una oveja de cada lado y luego quito la mitad de cada lado’. La combinación del uso de estrategias similares por distintos estudiantes, que hacían referencia explícita al contexto de la balanza, y las explicaciones sobre la resolución de los problemas en términos de acciones sugiere que las experiencias de los estudiantes de trabajar con la balanza podrían haber constituido una base para la fase posterior de resolución de ecuaciones lineales en un nuevo contexto.

Episodio 4: resolución de un sistema de ecuaciones simbólicas

En el último episodio de la secuencia de enseñanza, los estudiantes tenían que resolver un sistema de dos ecuaciones lineales simbólicas con dos incógnitas. Como se ilustra en la Figura 6, Kees (véase también el episodio 1) consiguió resolver este problema mostrando que F = 6 y H = 12. Primero convirtió las ecuaciones en balanzas, anotando las incógnitas de manera expandida. Después, conectó las F de ambos lados de la balanza y señaló la presencia de elementos idénticos en ambos lados de la ecuación. A continuación, tachó estas incógnitas para evidenciar el proceso de cancelación, consiguiendo aislar una F a la derecha de la ecuación. De este modo, Kees pudo deducir el valor de esta incógnita resolviendo la operación 19 − __ = 13. Por último, sustituyendo la incógnita F por el valor 6 en la segunda balanza (representación de la segunda ecuación), consiguió calcular el valor de H.

Figura 6. Solución de Kees de un sistema de dos ecuaciones lineales simbólicas, en combinación con la respuesta F = 6 y H = 12 (Episodio 4).

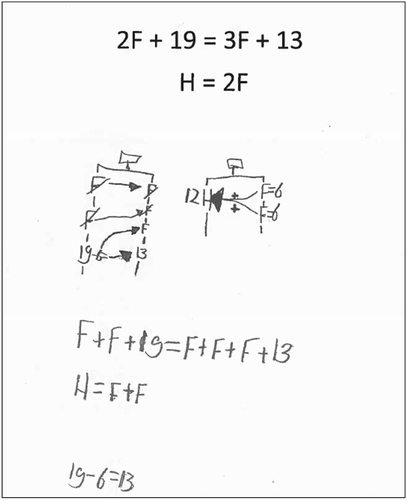
Como Kees, muchos estudiantes convirtieron primero las ecuaciones en balanzas antes de realizar la simplificación de términos idénticos. Otros estudiantes razonaron directamente sobre la ecuación representada simbólicamente. Por ejemplo, Kira repitió la primera ecuación simbólica y luego escribió ‘se añade 1F’, indicando que había percibido que en el lado izquierdo de la primera ecuación hay dos F, mientras que en el lado derecho hay tres. Entonces razonó que podía hacer la resta ‘19 – 13 = 6’ para llegar al valor de ‘1F = 6’. Por último, Kira utilizó este resultado para determinar el valor de H: ‘2F = 12’.

Este último episodio reveló que la mayoría de los estudiantes, que estaban aprendiendo a resolver ecuaciones lineales en un entorno de aprendizaje corporizado, fueron capaces de resolver sistemas de dos ecuaciones lineales simbólicas. La mayoría no tuvo dificultades para comprender la notación simbólica de las incógnitas. Kees, por ejemplo, mostró que comprendía que 2F es una forma abreviada de representar F + F. No obstante, no resolvió el problema de una forma simbólica formal, sino que, antes de aplicar la estrategia de aislamiento y después la estrategia de sustitución de valores, recurrió primero al modelo de la balanza. Este es un ejemplo que muestra que al menos algunos estudiantes experimentaron el modelo de la balanza como una potente herramienta que aplicaron para resolver ecuaciones lineales en el nivel formal. Otros estudiantes, como Kira, razonaron directamente utilizando las ecuaciones simbólicas.

Kees y Kira, por ejemplo, como la mayoría de los estudiantes que participaron en el estudio, no parecieron tener problemas con las ecuaciones que no estaban escritas de forma estándar (e.g., a + b = c), como, por ejemplo, ecuaciones que tenían incógnitas en ambos lados de la ecuación (e.g., 2F + 19 = 3F + 13 o H = 2F). Los estudiantes no aparentaron tener concepciones erróneas sobre el signo igual, en el sentido de que, en vez de interpretarlo como un signo que ‘después va la solución’, lo consideraron como un signo que refleja la igualdad de las expresiones a sus lados. Las actividades realizadas con las balanzas, en las que nuestro objetivo principal era que los estudiantes desarrollasen estrategias dirigidas a mantener la igualdad de las ecuaciones y, por tanto, facilitarles una base para resolver ecuaciones en el futuro, parecen haber contribuido a su comprensión del signo igual, incluso en las ecuaciones expresadas formalmente.

Discusión

En este estudio, investigamos el desarrollo del razonamiento algebraico de los estudiantes en un entorno de aprendizaje corporizado y la posible relación entre las características del entorno de aprendizaje y las estrategias algebraicas utilizadas por ellos. En los tres episodios consecutivos durante los que los estudiantes resolvieron problemas que incluían sistemas de dos ecuaciones lineales, se observó un progreso claro de su nivel de razonamiento y su índice de éxito. Al principio, más de la mitad de los 65 participantes mostraron formas de razonamiento que no usaban la información proporcionada por las ecuaciones dadas. Durante la secuencia de enseñanza, este porcentaje se redujo aproximadamente a un quinto de los estudiantes. Asimismo, mientras que, al principio, menos de un quinto de los estudiantes mostró el mayor nivel de razonamiento, combinando la información de las dos ecuaciones, después de la secuencia de enseñanza, más de la mitad de los estudiantes alcanzaron ese nivel de razonamiento. El progreso observado en el aprendizaje individual corrobora estos resultados. El razonamiento de la mayoría de los estudiantes mejoró con el tiempo sin mostrar ningún retroceso. En 14 estudiantes no se observó ningún cambio, 15 mostraron un patrón variable y solo cuatro mostraron un retroceso en su nivel de razonamiento. Un análisis posterior de las producciones escritas de los estudiantes en las tareas de evaluación reveló que también habían mejorado su habilidad para explicar su razonamiento y las estrategias que habían utilizado para resolver estas tareas.

Muchos estudiantes fueron reticentes a escribir sus razonamientos. En cada clase, durante la secuencia de enseñanza, observamos fluctuaciones en la predisposición de los estudiantes para escribir sus razonamientos. Esto podría explicar los patrones de razonamiento variable o decreciente de algunos de ellos. Otra explicación tiene que ver con las características de la tarea de evaluación del episodio 4. Mientras que, en las tareas de evaluación de los episodios 2 y 3, los estudiantes tenían que identificar relaciones entre las incógnitas, en la tarea de evaluación del episodio 4 tenían que hallar los valores de las incógnitas. Podría ser que pedirles que hallaran los valores de las incógnitas (comparado con pedirles que identificasen relaciones entre las incógnitas) hizo que les pareciese más sencillo encontrar una respuesta correcta y no escribieran su razonamiento. Como nuestra clasificación de los niveles de razonamiento de los estudiantes estaba basada en sus explicaciones escritas, tuvimos que asignar a estos estudiantes al nivel R0 (‘el estudiante no utiliza ninguna de las dos ecuaciones’) si no habían escrito nada. De los 19 estudiantes que mostraron un patrón variable o decreciente de razonamiento, 11 mostraron un retroceso en su nivel de razonamiento entre el episodio 3 y el 4, aunque que 10 de estos 11 estudiantes completaron correctamente la tarea de evaluación del episodio 4. Esto parece confirmar esta segunda explicación.

Hemos observado indicios de la existencia de una relación entre las características del entorno de aprendizaje corporizado y el razonamiento algebraico de los estudiantes. Ciertos tipos específicos de razonamiento, usos de estrategias y formas de notación podrían estar relacionados con sus experiencias (físicas) durante las actividades con las balanzas. La influencia de estas experiencias parecía evidente cuando se plantearon los problemas en contextos distintos. En estos casos, los estudiantes utilizaron frecuentemente estrategias similares a las que utilizaron con la balanza. Por tanto, parece que las estrategias que habían adquirido sentaron las bases para resolver nuevos problemas. Esto resultó más evidente cuando los estudiantes recurrieron a estrategias de restructuración, aislamiento y sustitución para resolver sistemas de dos ecuaciones lineales simbólicas. La balanza pareció convertirse en un modelo al que recurrir para resolver ecuaciones en un nivel formal. Un ejemplo de ello es el razonamiento mostrado por Kees en su resolución de la tarea de evaluación del episodio 4 (véase Figura 6), en la que claramente usó el modelo de la balanza para resolver un sistema de dos ecuaciones lineales escritas formalmente.

En línea con la teoría de la cognición corporizada (e.g., Wilson, 2002), asumimos que las experiencias motoras y sensoriales de los estudiantes con las balanzas podrían ser beneficiosas para sus habilidades de resolución de ecuaciones lineales. Durante la secuencia de enseñanza, los estudiantes podían percibir directamente cómo influían en el estado de equilibrio — que representa la igualdad de una ecuación lineal — sus manipulaciones de las bolas en la balanza. Esperábamos que esta combinación acción-percepción fundamentara la comprensión de los estudiantes sobre la igualdad, un concepto crucial en la resolución de ecuaciones lineales (e.g., Bush & Karp, 2013; Knuth et al., 2005; Li et al., 2008), en las experiencias corporizadas de mantenimiento del equilibrio. El resultado de esta posible combinación quedó patente en el razonamiento de los estudiantes en el episodio 3, cuando utilizaron estrategias algebraicas y dieron explicaciones en términos de acciones que podrían estar relacionadas con su actividad con la balanza. No obstante, el diseño de este estudio nos impide decidir a ciencia cierta la veracidad de nuestras suposiciones sobre los mecanismos que gobiernan el desarrollo del razonamiento algebraico de los estudiantes al interaccionar con la balanza física.

Además de los resultados referidos, cabe destacar que la mayoría de nuestros estudiantes, cuando tuvieron que resolver dos ecuaciones lineales, no parecían tener las dificultades que suelen mencionarse en otros estudios. Por ejemplo, no parecían carecer de comprensión relacional del signo igual (e.g., Behr et al., 1980; Carpenter et al., 2003). Los estudiantes mostraron esta comprensión relacional en las tareas de evaluación de los episodios 3 y 4, al interpretar correctamente el signo igual como una señal de equivalencia, en lugar de como una señal de ‘hacer’. Esto resulta llamativo, ya que, según el currículum de matemáticas, los estudiantes solo tienen experiencia del signo igual en tareas estándar (e.g., a + b = c). Otras tareas en formatos no estándares (e.g., c = a + b o a + b = c + d), que podrían fomentar una interpretación relacional del signo igual, apenas se abordan en el currículum. Obviamente, nuestro enfoque con la balanza, que se centra en el desarrollo de estrategias para mantener el equilibrio en las ecuaciones, ayudó a los estudiantes a adquirir una comprensión relacional del signo igual.

Además, los estudiantes de nuestro estudio tampoco mostraron dificultades con la notación simbólica formal de las ecuaciones (e.g., Koedinger & Nathan, 2004) ni con las operaciones con incógnitas (e.g., Filloy & Rojano, 1989; Herscovics & Linchevski, 1994). Ser competente en la resolución de este tipo de problemas significa que los estudiantes no solo tienen que comprender las ecuaciones dadas, sino que además tienen que ser capaces de manipularlas y combinarlas para utilizar esa nueva información recabada sobre las incógnitas para resolver los problemas. Para estudiantes de primaria, a quienes nunca se les ha enseñado a resolver ecuaciones lineales, es algo que realmente requiere un pensamiento de alto nivel. Así pues, los resultados de nuestro estudio corroboran claramente el consenso general existente sobre la necesidad (véase e.g., National Council of Teachers of Mathematics [NCTM], 2000) de crear las bases para un pensamiento de alto nivel ya en educación primaria.

Al interpretar los resultados de nuestro estudio, es importante tener en cuenta diversas limitaciones. En primer lugar, el carácter exploratorio del estudio nos permitió explorar el desarrollo del razonamiento algebraico de los estudiantes participantes. No obstante, existen ciertas limitaciones relacionadas con este diseño, como la ausencia de un grupo de control, por lo que los resultados deben ser interpretados con cautela. Es necesario, por tanto, llevar a cabo investigaciones adicionales de carácter experimental para analizar con mayor detalle la influencia que ejercen las experiencias en un entorno de aprendizaje corporizado, como el de las balanzas, sobre el razonamiento algebraico.

La segunda limitación está relacionada con el método de medición del razonamiento de los estudiantes. Nuestra clasificación del nivel de razonamiento de los estudiantes se basó en las respuestas escritas y no en protocolos de ‘pensar en voz alta’. Por tanto, es posible que no se haya capturado del todo su razonamiento y, en consecuencia, que se haya subestimado su nivel de razonamiento. Esto también lo sugiere la observación de que algunos estudiantes mostraran gran capacidad para explicar su razonamiento de manera verbal durante las lecciones pero no escribieran sus procesos de razonamiento con el mismo nivel de sofisticación en las tareas de evaluación. Otro aspecto digno de consideración es la evaluación repetida de la resolución de ecuaciones lineales, que podría haber ofrecido a los estudiantes más oportunidades para aprender a resolver estos problemas. Por tanto, es importante reconocer que, además del efecto de las experiencias con la balanza, el mero hecho de resolver las tareas de evaluación podría haber contribuido a mejorar el nivel de razonamiento de los estudiantes. Además, resolver las tareas de evaluación inmediatamente después de las actividades de aprendizaje, y que esas tareas se centrasen en el mismo contenido que el trabajado en las lecciones, podría haber influido en los resultados de los estudiantes en las tareas. Una evaluación más retrasada en el tiempo tal vez hubiese proporcionado una visión mejor de los beneficios obtenidos por los estudiantes en las lecciones.

Otra preocupación es que, aunque nuestro estudio se realizó en un contexto de clase ordinaria, la investigadora fue quien dirigió las lecciones. Esto quiere decir que podemos preguntarnos si este tipo de enseñanza algebraica con aparatos concretos puede llevarse a cabo en la práctica educativa habitual. Además, podemos preguntarnos si los profesores de educación primaria están preparados y se sienten seguros para enseñar este tipo de lecciones.

Una pregunta que tampoco hemos respondido es si la enseñanza de la resolución de ecuaciones lineales utilizando balanzas puede llevarse a cabo en la trayectoria más prolongada de enseñanza del álgebra. En nuestro estudio, la resolución de ecuaciones lineales se trató de manera bastante breve e incluyó solamente ecuaciones con números positivos y sumas. Es necesario investigar en mayor detalle si el uso de balanzas puede servir para otros tipos de ecuaciones que tengan números negativos o restas, que no pueden representarse utilizando este modelo particular. Como han destacado otros autores (e.g., Fyfe, McNeil, Son, & Goldstone, 2014), podría ser necesario un proceso de disminución de la concreción, comenzando con representaciones visuales y progresando gradualmente hacia símbolos abstractos.

A pesar de las limitaciones señaladas, nuestros resultados muestran que los estudiantes de quinto curso de primaria son capaces de aplicar correctamente estrategias algebraicas tales como la reestructuración, el aislamiento y la sustitución para la resolución de ecuaciones lineales. Por tanto, el entorno de aprendizaje corporizado de nuestro estudio parece haber constituido una base para el razonamiento algebraico en etapas posteriores, en las que se resuelven sistemas de ecuaciones lineales presentadas simbólicamente.

Acknowledgements / Agradecimientos

Research was conducted at the Faculty of Social and Behavioural Sciences, Utrecht University, Heidelberglaan 1, 3584 CS Utrecht, the Netherlands. This work was supported by the Netherlands Initiative for Educational Research [405-14-303].[c/e note: translation of this line TBC] / Esta investigación se llevó a cabo en la Facultad de Ciencias Sociales y del Comportamiento de la Universidad de Utrecht. Heidelberglaan 1. 3584 CS Utrecht, Holanda.

Disclosure statement

No potential conflict of interest was reported by the authors. / Los autores no han referido ningún potencial conflicto de interés en relación con este artículo.

Supplemental data

Supplemental data for this article can be accessed here.