Does the duration of professional development programs influence effects on instruction? An analysis of 174 lessons during a national-scale program

ABSTRACT

We examine the effects of a year-long national-scale professional development (PD) program on mathematics instructional quality. In contrast to previous studies examining the effects of this program on instruction by comparing before and after participation or participants and non-participants, we examine whether instructional quality changed during the program. More specifically, we conduct an analysis of 174 video-recorded mathematics lessons given by 52 teachers during their year of participation. Contrary to previous studies, the results demonstrate that the instructional quality did not improve over the course of the PD. We suggest that the explanations for the diverging results concern how, when, and to what extent instructional quality changes in PD programs. Specifically, we discuss how the explanations may illuminate the significance of PD duration for PD effects, and how these effects may be mediated by features concerning the PD content and the scale at which the program is implemented.

KEYWORDS:

• Classroom observations
• instructional quality
• mathematics instruction
• teacher professional development

Introduction

Teachers’ professional development (PD) is widely regarded as a key to improving student learning outcomes (e.g. Darling-Hammond, Hyler, and Gardner 2017; OECD 2018), and governments invest billions in teacher PD annually with the intention of enhancing teachers’ knowledge and instructional practice (e.g. Kraft, Blazar, and Hogan 2018). Correspondingly, scholars have put great effort into identifying PD features that may improve instructional practices and student results (e.g. Darling-Hammond, Hyler, and Gardner 2017; Desimone 2009). However, studies (Garet et al. 2016; Jacob, Hill, and Corey 2017; Lindvall et al. 2021) have shown it to be notoriously difficult to affect instructional practices and student achievement, even when the offered programs can be regarded as ‘state of the art’ in relation to such features. Thus, although the critical features may be important they are not sufficient on their own, and we need further studies with the potential to refine the critical feature conceptual frameworks (Kennedy 2016).

This study particularly addresses one of the critical features: duration – i.e. that the PD should include multiple sessions spread over a longer period of time. The reasons for emphasising this particular feature are twofold. First, even though review studies (e.g. Darling-Hammond, Hyler, and Gardner 2017; Kennedy 2016) have presented several examples of PD programs of sustained duration that have shown positive effects on instructional practices and/or student achievement, recent meta-analyses (e.g. Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019) show no significant effect of duration on changes in instructional quality. Second, one of the core arguments for the need of extended duration is that one-off workshops afford insufficient time for rigorous and cumulative learning, and merely help participants acquire discrete pieces of knowledge that are easily translated into practice (Darling-Hammond, Hyler, and Gardner 2017). However, although this may be true, it is unclear whether PD programs of extended duration succeed in developing deep knowledge. In fact, studies indicate that PD programs emphasising discrete instructional behaviours have greater effects on student achievement than those advocating new approaches to teaching a particular curricular content (Desimone and Garet 2015). Thus, research has raised questions concerning whether, how, and in which circumstances duration influences PD outcomes, and there is a need for research on the role and significance of PD duration. Particularly in-depth studies that follow classroom practices over the course of the PD, rather than just at the beginning and the end, have been called for (Garrett, Citkowicz, and Williams 2019).

In this study, we aim to contribute to the understanding of the role and significance of PD duration for changes in instructional quality. We do this by investigating the case of Boost for Mathematics (BfM), a Swedish state-coordinated PD program with a participation rate of nearly 80% of all school mathematics teachers in Sweden (about 35,000 teachers) and that corresponds well with the quality criteria in established frameworks for high-quality PD. More precisely, by conducting an analysis of 174 video-recorded lessons given by BfM participants during their year of PD participation, we examine if, when, and what changes in instructional quality occurred over the course of the PD.

Background

It has been argued that all PD programs aiming to improve student achievement rest on at least two, sometimes implicit, theories (Wayne et al. 2008). The first concerns how the changed instructional practices will lead to improvements in student achievement. We will call this a theory of instruction. The second concerns the program’s underlying assumptions about what causes increases in teachers’ knowledge and/or instructional practices and how this comes about. We will call this a theory of instructional change as we focus on changes in instructional quality. Studies of impacts of teacher PD need to consider both these theories; otherwise, it is impossible to identify the causes of effects or lack of effects.

PD programs’ theories of instruction

What constitutes high-quality mathematics instruction has been debated (cf. Hmelo-Silver, Duncan, and Chinn 2007) and will likely remain controversial. However, one element that has been widely included in visions of high-quality mathematics instruction in the past two decades is the importance of attending to students’ mathematical thinking (Jacobs and Spangler 2017). This is also an important foundation in recent work on ambitious instruction by leading scholars in the field of mathematics education (e.g. Cobb et al. 2018; Schoenfeld et al. 2019). Ambitious mathematics instruction entails, among other things, core instructional practices such as teachers’ orchestration of classroom discussions, noticing students’ mathematical thinking, and establishing equitable learning environments. Teachers may, for example, support students in solving cognitively demanding tasks, press them to provide evidence for their reasoning, and use assessment to solicit student thinking and modify subsequent instruction to respond to these ideas.

Even though there seems to be high agreement among researchers regarding high-quality mathematics instruction, PD programs carried out in practice have been shown to differ in their theories of instruction (Munter, Cobb, and Shekell 2016). For example, programs differ in their goals for students’ learning. While some focus on memorisation and the smooth execution of procedures in order to arrive at the correct answer, others emphasise conceptual understanding of central mathematical ideas. Programs also differ in their assumptions of how instruction should be organised to support learning. While some focus on students’ development of procedural fluency prior to their application in problem-solving situations, others emphasise that procedural fluency develops along with (or as a result of) the development of conceptual understanding.

PD programs’ theories of instructional change

Scholars (e.g. Desimone 2009; Penuel et al. 2007) have argued that research is sufficiently unanimous to declare a consensus on five core critical features of high-quality teacher PD that are necessary to induce improved instruction: Content Focus means that the focus of PD programs should be subject matter and the learning and representation of that subject matter; Coherence suggests that PD programs should be consistent with policies on different levels and with teachers’ knowledge and beliefs; Active Learning implies that teachers need to engage in the analysis of teaching and learning, for example by observing teaching, or planning lessons; Collective Participation means that PD programs are directed at all teachers in a grade, school subject, or school; and finally, Duration implies that PD should take place regularly over an extended period of time.

However, in light of empirical findings, the list of core critical features cannot be seen as settled. First, reviews of effective PD have identified additional features associated with improved instruction and student achievement, such as individualised coaching and modelling of effective teaching (Darling-Hammond, Hyler, and Gardner 2017; Garrett, Citkowicz, and Williams 2019). Second, specifications of the original features have been suggested. For example, the results of a review (Desimone and Garet 2015) indicate that PD programs with a content focus emphasising specific teacher behaviours tend to have stronger positive effects than those aiming to improve teachers’ subject matter knowledge and/or to change more complex instructional behaviours. Third, some of the original features have even been questioned. For example, meta-analyses have found that programs including a content focus on specific subject matter do not induce greater effects on instruction and student achievement than those without (Kennedy 2016; Kraft, Blazar, and Hogan 2018). Moreover, as this article focuses on, PD programs of different durations seem to produce similar effects on instruction and student results (Basma and Savage 2018; Kennedy 2016; Kraft, Blazar, and Hogan 2018), sometimes even regardless of whether duration is measured as the total number of contact hours within the PD or the intensity with which these hours were distributed (Garrett, Citkowicz, and Williams 2019). In fact, some evidence suggests that short programs (<26–30 weeks) have greater impact than longer ones (Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019). Although these reviews were unable to identify why longer programs did not produce greater effects, some authors suggested likely causes. One such cause is that shorter interventions may be easier to conduct with high quality, which is more important than an extended duration (Basma and Savage 2018; Kraft, Blazar, and Hogan 2018). This claim is in line with a finding that programs of longer duration had more variability in their effects than shorter programs (Garrett, Citkowicz, and Williams 2019). It is also in line with Kennedy’s (2016) result that PD intensity was associated with weaker PD effects when the PD was mandatory and implemented at a larger scale. Other suggested causes for the lack of demonstrated duration effects are that shorter programs may focus on instructional strategies that are easier to implement (Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019), or that they may disrupt ordinary teaching less (Basma and Savage 2018).

The investigated PD program

BfM is a national-scale PD program initiated by the Swedish Government and run by the Swedish National Agency for Education (SNAE). Although participation is voluntary for municipalities and schools (but, notably, not for teachers, whose participation is determined by their employer), the level of participation in BfM has reached almost 80% of all Swedish mathematics teachers in Grades 1–9.¹ One explanation for this high participation rate is that the state provides financing for each partaking teacher on the condition that the PD realisation adheres to the instructions provided by the SNAE.

The program’s design is based on modules, each requiring one semester. The modules (with some exceptions) are structured around the core mathematical content in the national curriculum and grade levels (1–3, 4–6, and 7–9), for example Number Sense in Grades 1–3.² All modules include eight rounds consisting of four sessions each, in which teachers: (A) individually study PD materials (e.g. texts, video) available on a digital platform; (B) meet with a coach (ordinary teachers receiving specific training on the PD model and appropriate conversation techniques) and their teacher colleagues at the respective schools to reflect on the materials and plan a teaching activity; (C) carry out the activity with the class they normally teach; and (D) meet again with the coach and their colleagues to discuss their experiences from the teaching activity.

BfM’s theory of instruction

Because the BfM modules differ in their mathematical content and were developed by different groups of researchers and teachers at Swedish universities, BfM contains elements from several theories of instruction. However, common to all modules is the inclusion of four didactical perspectives that were obligatory content. To ensure that modules adhered to this obligation, each module was reviewed in several iterative cycles by employees at the SNAE and at least two external advisers (often mathematics didactic researchers with their own experience of module development).

The first didactical perspective, Assessment for teaching and learning, focuses on teachers’ use of formative assessment practices, often referring to frameworks such as Wiliam’s (2007). The second perspective, Socio-mathematical norms, emphasises issues concerning student agency and authority. The theoretical basis mentioned in the modules is typically Yackel and Cobb’s (1996) paper on socio-mathematical norms, or Brousseau’s (1997) concept of didactical contract. The third perspective, Teacher routines for interaction in the classroom, is broader and the content in the modules reflecting this varies. However, frequently occurring themes are teacher questioning in the classroom and how to orchestrate productive mathematical discussions (cf. Smith and Stein 2011). The fourth perspective, Teaching in accordance with the mathematical competencies, concerns instruction designed to foster the five mathematical competencies mentioned in the national curriculum, for example the formulation and solving of mathematical problems, and the application of mathematical reasoning.

Overall, the four didactical perspectives that constitute the basis of BfM’s theory on instruction are in line with the previously discussed features of ambitious mathematics instruction. However, results from observations of nearly 200 elementary school teachers have demonstrated that such instructional practices differ from the typical teaching in Swedish classrooms (Boesen et al. 2014). According to these observations, Swedish mathematical lessons mostly offer students opportunities to develop procedural competency, whereas opportunities to practice other mathematical competencies (e.g. problem-solving, mathematical reasoning) arise more rarely.

BfM’s theory of instructional change

An analysis of the official reports motivating and suggesting the design of BfM revealed that, even though the design principles are not always explicitly formulated in the documentation, they largely conform to established research frameworks for teacher PD (Boesen, Helenius, and Johansson 2015). For example, BfM corresponds well with the five core critical features of effective PD. First, in terms of Content Focus, BfM emphasises specific subject matter in mathematics instruction, as well as how students learn this content and how it should preferably be taught. Second, rather than passively attending lectures, teachers in BfM are engaged in Active Learning activities, such as designing, trying out, and evaluating instructional practices. Third, BfM entails Collective Participation, with all mathematics teachers at participating schools expected to partake in the program and jointly discuss the PD content during coach-led sessions. Fourth, the PD sessions comprise around 60 hours of work (excluding the lessons in which the planned teaching activities are enacted) evenly spread out over the year (Duration). Finally, Coherence with policy and teacher’s priorities is ascertained, in that the modules are required to emphasise teaching in accordance with the mathematical competencies in the national curriculum, and the PD materials are tried out with practicing teachers before inclusion in the publicly available BfM material.

It can also be noted that BfM corresponds with additional features of high-quality PD in the literature, at least at a surface level. For example, the PD content is explicitly linked to classroom practices (Desimone and Garet 2015), although this is realised by asking teachers to plan lessons which they carry out in their classes, rather than that adapting the program to the mathematical content they are currently teaching. Moreover, BfM provides external support (Darling-Hammond, Hyler, and Gardner 2017) in the form of trained coaches. However, rather than guiding teachers based on the coaches’ expertise in mathematics didactics, their role is primarily to serve as conversation leaders during the collegial meetings (Kirsten and Carlbaum 2020).

Previous studies of BfM

A few studies have emphasised BfM’s effects on instruction and student achievement, and shown somewhat contrasting results. Firstly, Lindvall, Helenius, and Wiberg (2018) used a mathematical test closely aligned to the PD module used by investigated teacher groups and found a small but positive impact on students’ mathematics achievement in the upper grades of elementary school (Grades 8 and 9), but no impact in Grades 2–7. Secondly, Lindvall et al. (2021), on the other hand, found no effect on student mathematics achievement as measured in TIMSS results when comparing students whose teachers did and did not participate in BfM. However, the study demonstrated a small but statistically significant effect on instructional change as measured through teachers’ and students’ questionnaire responses. Thirdly, a national evaluation (Österholm et al. 2016) was based on observations of around 50 elementary school teachers’ mathematics lessons. The observations were carried out twice for each teacher at one-year intervals, either before and during or during and after participation in BfM. By analysing the classroom observations in relation to each of BfM’s four didactical perspectives, a score was calculated at each point of data collection. Statistical analyses demonstrated significant differences in the mean score before and during participation in BfM for the three didactical perspectives Teaching in accordance with the mathematical competencies, Teacher routines for interaction in the classroom, and Assessment for teaching and learning. For the interval during and after participation in BfM, no statistically significant difference was found for any of the didactical perspectives, which indicates that the instructional changes remained a year after teachers’ participation in the program.

In summary, previous studies have shown statistically significant effects on instruction, but limited or no effects on student achievement. We seek to shed further light on these findings and complement previous studies by using new datasets and methods for data collection and analyses. As we will elaborate on in the Discussion section, there may be methodological reasons for the contrasting results, but the discrepancies may also illuminate how critical features such as duration influenced PD effects.

Materials and methods

Empirical material

The data used in this study comes from a larger research project in which 52 teachers were followed over the course of a year of participation in BfM. The teachers worked in three municipalities across Sweden, and the 19 schools where they taught were located in both urban and rural areas as well as in areas with different socioeconomic conditions (see Appendix A). To capture the variation in socioeconomic status (SES) in the statistical analyses, we used the proportion of students at the school who have a parent with a tertiary education, which ranged from 21 to 89% (M = 53.8%).

The dataset for this study consists of 174 video-recorded lessons: 84 in Grades 1–3, 61 in Grades 4–6, and 29 in Grades 7–9. The lessons were evenly spread, and recorded, during the year in which the participating teachers took part in BfM with financial support (between 4 September 2015 and 2 June 2016). Each teacher was recorded an average of 3–4 times while participating in BfM (for more detailed information, see Appendix A). According to the Swedish law (2003: 460) on ethical review of research concerning people, no institutional ethical review or approval was necessary for the kind of data used in this study. The teachers and students (including their caregivers), participating in the video-recorded lessons were informed, and approved, that the collected data would be used to contribute to research on teacher PD and that their participation in the research project was completely voluntary.

The video-recorded lessons were those in which teachers enacted teaching activities suggested by the BfM modules, for example asking students to formulate their own mathematical problems or conducting a lesson focusing on the use of letters in algebra. Thus, the enactment of these teaching activities often interrupted the ordinary lesson sequence, which was often visible in the video-recordings. For example, some teachers started these lessons by stating that it was going to be a ‘BfM lesson’.

Observation instrument

The UTeach Observation Protocol (UTOP) (Marder et al. 2010) was used to code the instructional quality in the video-recorded lessons. The reasons for choosing UTOP were several. First of all, a strength of the UTOP is that there is psychometric data on its reliability and validity (e.g. Kane and Staiger 2012; Walkington and Marder 2018). However, the evidence supporting validity arguments may be sensitive to the contexts surrounding test implementation, and the interpretation of scores intended by researchers may require modification in specific contexts. Therefore, in the following sections we will discuss validity issues of particular importance for this study (e.g. consistency in scoring, connections to valued aspects of instructional quality).³

A second reason for choosing UTOP was that, compared to other well-established observation instruments, UTOP shows higher correlation between observation overall score and student achievement (Kane and Staiger 2012). Our analysis was based on a version of the UTOP protocol containing 22 indicators that have also been used in the Measures of Effective Teaching (MET) study (Kane and Staiger 2012). However, three indicators were excluded from our analysis. The Lesson Reflection indicator was excluded because it is based on data from teacher interviews rather than teacher observations, while the Classroom Interaction and Content Abstraction indicators were excluded as they did not apply to several lessons in our dataset, because many lessons did not include group work or elements of mathematical abstraction.

A third reason for choosing UTOP was that it rests on theories of instruction which largely correspond with features of the ambitious mathematics instruction that is typical of recent research-based large-scale teacher PD programs (Cobb et al. 2018; Schoenfeld et al. 2019). More specifically, the UTOP indicators rest on theories regarding ambitious instruction that can be summarised into six fundamental foci (cf. Walkington and Marder 2018). Effective communication of STEM content connects to teachers’ pedagogical content knowledge and includes practices such as exploring student misconceptions, and giving clear explanations. Problem-based and discovery learning emphasises student agency for developing methods for solving mathematical problems, rather than being given ready-to-use procedures to use in routine tasks. Facilitating intellectual engagement includes teacher strategies that support students in deeply engaging in the mathematical content, for example by providing just enough scaffolding to allow them to struggle with the important mathematics. Classroom management concerns how to establish order in the classroom and includes issues related to setting classroom rules effectively, and facilitating a high time-on-task. Lesson structuring and assessment emphasises a well-organised lesson with a clear sequence to build conceptual understanding of important mathematical ideas, and assessment practices connected to both formative and summative measures of student learning. Finally, Equity, diversity, and access involves instructional practices aimed at involving all students, irrespective of characteristics such as SES.

A fourth reason for choosing the UTOP was that the UTOP indicators and the six fundamental foci on which they rest correspond in several ways with BfM’s four didactical perspectives. The UTOP indicators corresponding with BfM’s didactical perspectives are summarised in Table 1.

Table 1. UTOP Indicators.

UTOP indicators corresponding with BfM’s didactical perspectives
1. The teacher used formative assessment effectively to be aware of the progress of all students, and modified the lesson appropriately when formative assessment demonstrated that students did not understand.
2. The classroom environment facilitated by the teacher encouraged students to generate ideas, questions, conjectures, and/or propositions that reflected engagement with or exploration of important mathematics and science concepts.
3. The teacher used questioning strategies to encourage participation, check on skill development, and facilitate intellectual engagement and productive interaction with students about important science and mathematics content and concepts.
4. The teacher involved all students in the lesson (calling on non-volunteers, facilitating student-student interaction, checking in with hesitant learners, etc.).
5. The structure of the lesson allowed students to engage with and/or explore important concepts in mathematics or science (instead of focusing on techniques that may only be useful on exams).
6. The lesson included an investigative or problem-based approach to important concepts in mathematics or science.

However, the UTOP also captures several aspects of instruction that BfM does not explicitly aim to influence. Examples of UTOP indicators not corresponding with BfM’s four didactical perspectives are ‘The majority of students were on task throughout the class’ and ‘Appropriate connections were made to other areas of mathematics or science and/or to other disciplines’. Note that some of these UTOP indicators may be treated in particular BfM modules. However, only those corresponding with the four didactical perspectives are valid for all BfM modules.

Data coding

Each UTOP indicator is rated on a five-point Likert scale. The rating scale for most items corresponds with two descriptors: one that measures the frequency of the indicator’s occurrence (e.g. observed rarely, observed often), and one that captures the quality of the implementation of that indicator (e.g. demonstrated poorly, demonstrated well). In the coding guide, each indicator is described with a general rubric that is associated with each rating score (1–5). For example, Figure 1 demonstrates the general rubric and description of indicator and rating scores for Indicator 4 in Table 1.

Figure 1. Description of an UTOP Indicator and Rating Scores (Marder et al. 2010, 29–30).

The indicator concerns teachers’ questioning of techniques, and raters are instructed to take into account both the number, function, and quality of the teacher’s questions. During the coding process, observers rate each item and write down supporting evidence justifying their indicator ratings, typically referring to the guidelines in the general rubrics. For instance, in relation to the coding of Indicator 4 (see Figure 1) in one of the video-recorded lessons in this study, one of the authors wrote:

The teacher regularly asked factual questions about the mathematics content. However, she rarely challenged students with questions that promoted deeper understanding and explored misconceptions, even though misconceptions were apparent in the lesson. This corresponds with the description of a rating score of 3.

The lesson ratings in this study were conducted by the first and fourth authors. Approximately 30% of the lessons were rated by both authors to control for inter-rater reliability in terms of Cohen’s kappa. The inter-rater agreement score was .74 (corresponding with 81% agreement), which is interpreted as well above substantial agreement. This holds true when the value is compared both to standard values of inter-rater agreement (Landis and Koch 1977) and to previous studies in which the UTOP has been used (e.g. Walkington and Marder 2018). After calculating the inter-rater reliability score, both coders discussed the non-compliant items based on their notes for their respective ratings until consensus was reached.

Data analysis

Based on the UTOP ratings, we computed two scores for each of the 174 lessons. The UTOP Sum Score was calculated as the sum of the 19 items (theoretical range 19 to 95). Based on a subset of six of these 19 items (theoretical range 6 to 30) deemed as those corresponding with BfM’s four didactical perspectives (see Table 1), we also calculated a UTOP BfM Score. As the latter variable is more proximal to the PD objectives, the PD effects on this variable should be greater (Ruiz‐primo et al. 2002). The internal consistency, measured using Cronbach’s alpha, for both variables (UTOP Sum Score=.90; UTOP BfM Score=.81) was high.

The objective of our analysis is to examine how instructional quality changed over time, using repeated measures of instruction for each teacher. To account for variation in the baseline instructional practice across teachers, we use a mixed-effects model with a random intercept at teacher level. An alternative analysis would involve subtracting each teacher’s initial instructional score from subsequent scores; this alternative analysis yields results that are qualitatively similar to those reported below. The key predictor is the variable Time, defined as the number of days since the first lesson was recorded on 4 September 2015. Because instructional practice may vary across educational stages, we included controls in the form of dummy variables for Grades 4–6 and 7–9 (i.e. Grades 1–3 serve as reference level). Because instructional practice may vary according to student composition, we also included a control for the SES of the student groups (the percentage of students at the school who had at least one parent with a higher education). This analysis assumes that the effect of time on instruction is similar across teachers. This assumption can be relaxed by including a random slope at teacher level. The results from this alternative analysis are similar to those reported below.

Results

The UTOP sum score

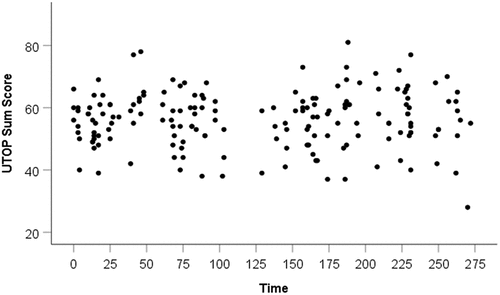
Across the 174 lessons, the UTOP Sum Score ranged between 28 and 81 (M = 56.21, SD = 8.98). Figure 2 shows the UTOP Sum Score of all lessons plotted against time. The gap at time 100–125 corresponds with Christmas break. The image shown in the scatter plot is simplified in that several important features of each data point are not shown (teacher, SES, educational stage). Nonetheless, the figure illustrates a remarkable lack of any discernible trend of UTOP Sum Score over time.

Figure 2. The UTOP Sum Score for 174 Lessons Plotted Against Time During the BfM Year .

In multi-level data, the intraclass correlation coefficient, ICC(1), can be used to describe the proportion of the total variance that can be attributed to variation at the higher level (Bliese, Maltarich, and Hendricks 2018). In our dataset, ICC(1) = 0.51, which means that slightly more than half of the variance in UTOP scores across lessons can be attributed to variation between teachers. Table 2 reports the results of the mixed-effects model, showing that 30% of the variation between teachers could be accounted for by the SES and educational stage of the student group. The effect of SES is notable: The estimate of 0.19 means that lessons in a class where all students have at least one parent with a higher education are expected to have a 19-point higher UTOP score than lessons in a class where no students have a parent with a higher education. Our main interest, however, is the effect of time on UTOP scores. As shown in Table 2, the effect of time was negligible and statistically non-significant.

Table 2. Estimated Fixed Effects on UTOP Sum Score.

	Fixed effect estimate	95% confidence interval
Intercept	43.95	[38.57, 49.33]
Time	0.003	[−0.010, 0.015]
SES	0.19	[0.10, 0.28]
Middle school	5.37	[1.42, 9.33]
High school	0.86	[−3.90, 5.63]
Proportion of variance explained
at the lesson level	0.05
at the teacher level	0.30

The UTOP BfM score

The UTOP BfM Score ranged between 8 and 27 (M = 18.83, SD = 3.24) across the 174 lessons, with ICC(1) = 0.42, which means that somewhat less than half of the variance in UTOP BfM scores across lessons can be attributed to variation between teachers. As reported in Table 3, the results of the mixed-effects model were similar to those reported for the UTOP Sum Score (taking into account that unstandardised effects will only be a third as large as only a third of the items are used for the BfM score). Thus, the effect of time was negligible and statistically non-significant, while there was a substantial effect of SES.

Table 3. Estimated Fixed Effects on UTOP BfM Score.

	Fixed effect estimate	95% confidence interval
Intercept	14.81	[12.93, 16.69]
Time	−0.000	[−0.005, 0.004]
SES	0.06	[0.03, 0.10]
Middle school	1.63	[0.23, 3.02]
High school	0.07	[−1.62, 1.77]
Proportion of variance explained
at the lesson level	0.04
at the teacher level	0.28

Discussion

The results of this study show that the quality of instruction did not increase over the course of BfM as measured in overall UTOP score. Even when we restricted the analysis to the theory of instruction explicitly advocated by BfM, we detected no change in instructional quality over time. We discuss these results in three sections. First, we recognise that the results must be interpreted in light of its limitations. Secondly, we note that our results stand in contrast to those presented in previous studies (Lindvall et al. 2021; Österholm et al. 2016). This does not necessary imply contradictions in results but may instead reflect study limitations and differences in when data was collected. As the various studies of BfM have their respective limitations and strengths, a comparison between them has the potential to provide a more complete picture of the program’s effects. Thirdly, the combined results from this and previous studies of our case of a large-scale PD program contribute to a more profound understanding of the core critical feature frameworks, especially with regard to the critical feature duration.

Limitations

One possible limitation of this study is our choice to use the six-item subset UTOP BfM Score, as it is not a part of the original UTOP structure. Particularly, there is a need to address the risk that the null effect on the BfM Sum Score is caused by increasing scores on some items and decreasing scores on others. The fact that the BfM Sum Score has good internal consistency (Cronbach’s alpha=.81) should alleviate this concern. Moreover, we found that if the mixed-effects analysis is performed on each separate item score instead of on the sum scores, there is no item for which time in the PD program has a statistically significant positive effect.

An additional limitation of this study is that the empirical material was not a random sample of the total population of BfM participants. Therefore, the results of the statistical analyses cannot be generalised to all BfM participants. However, the inclusion of control variables in the statistical analyses showed that PD duration had no statistically significant effects on instructional quality at particular educational stages or at particular levels of school SES. Also, our background knowledge of the participating schools indicated that their realisation of BfM was in line with how teachers worked nationally, as described in official evaluations of BfM. Finally, the fact that the 52 studied teachers volunteered to participate in the study should typically bias the results positively (e.g. Kennedy 2016) rather than yielding the lack of effect we found. Together, this indicates that a randomised sample would not have produced greater effects on instructional quality.

Moreover, we study the effect of PD duration and find that, on average and across participating teachers, the effect of duration is negligible. It is possible that this average result hides a systematic variation among teachers, such that the effect could be positive for more experienced teachers and negative for less experienced teachers. For example, empirical results indicate that PD affects mathematics instruction differently depending on teacher characteristics, such as their visions of high-quality instruction (Munter and Correnti 2017), contextual factors, such as the grades in which instruction is carried out (Britt, Irwin, and Ritchie 2001), and the socioeconomic status (SES) of the students (Roschelle et al. 2010). It is, however, out of the scope of this article to include analyses on between-teacher differences. However, future studies are encouraged to examine the between-teacher differences in what teachers change in their instruction throughout PD participation.

In addition to the limitations described above, the next section will also touch upon some limitations involving differences in the methodology between the present and previous BfM studies.

Comparison with the results of previous BfM studies

This study documents another mathematics teacher PD program incorporating established features of high-quality PD that still showed limited or no effects (cf. Garet et al. 2016; Jacob, Hill, and Corey 2017). However, in the case of BfM, this result contradicts previous studies’ findings that instruction changed in line with BfM’s objectives (Lindvall et al. 2021; Österholm et al., 2016). As the divergence between the studies’ results may be an effect of differences in empirical material and analytical instruments, or reveal significant aspects of how BfM’s program features influence instructional practices, we will compare the studies’ methodology, limitations, and results. Thus, we elaborate on three possible explanations for the diverging results among the studies.

First, a possible explanation for the differences in results between the three BfM studies is the choice of analytical instruments. Both 2016) and Lindvall et al. (2021) used scales created to capture aspects of instruction that BfM intended to influence. The present study used two scales: the broader UTOP Sum Score; and the narrower UTOP BfM Score, which was limited to items concerning BfM’s four didactical dimensions. Evidently, instruments may be more or less sensitive to certain instructional changes. For example, a broad measure like the UTOP Sum Score may fail to detect instructional change despite the fact that it happened. However, PD effects should reasonably be larger when gauged in a narrower measure, such as the UTOP BfM Score, which they were not. Thus, although we cannot exclude the possibility that the two UTOP scales are less sensitive to instructional changes than the instruments used by Österholm et al. (2016) and Lindvall et al. (2021), the similarity of the fixed effects for the UTOP Sum Score and the UTOP BfM Score provides no substantial support for this explanation of the diverging results among the studies.

Second, a methodological difference that may explain the diverging results among the three studies concerns the fact that BfM instructed participants to enact particular teaching activities in their ordinary classes. This means that the lessons in which the instructed teaching activities were enacted likely differed from the teachers’ typical instruction. In the Österholm et al. (2016) study, while both ordinary teaching and lessons with BfM teaching activities were observed, the study did not differentiate effects based on lesson type. In Lindvall et al. (2021), teachers and students were asked about the instructional practices in mathematics at large rather than in particular BfM lessons. In the present study, however, only lessons with BfM teaching activities were observed. Accordingly, one potential explanation for the lack of discernible effect in the present study is that the BfM teaching activities caused teachers to appear as beginners as they enacted new instructional methods at all observed lessons. In their ordinary lessons, though, it is possible that the teachers successively learned to master the new instructional approaches.

A third explanation for the diverging results concerns the timing of the observations. Österholm et al. (2016) observed teachers before and during or during and after BfM, and Lindvall et al. (2021) compared the instructional practices of BfM participants with those of a control group. In contrast, the present study included several observations of teachers during their participation in BfM, but neither before nor after the program. Thus, one explanation for the fact that Österholm et al. (2016) found statistically significant effects on changes in instructional quality between observations conducted before and during (but not between during and after) BfM, whereas the present study did not, may be that the quality of instruction improved very early in the PD program. If changes in instructional quality happened before the first observation in the present study but not since then, these changes would go undetected. This would also explain the differences in results between the present study and Lindvall et al. (2021), as the latter showed that the differences in instruction between BfM participants and non-participants were constant regardless of whether participation was ongoing or completed. Future studies of when instructional changes occur during PD programs would be valuable, to guide PD design and to understand the drivers and barriers to instructional change during PD.

In summary, the results reported by Österholm et al. (2016) and Lindvall et al. (2021) indicate that changes in instructional quality took place as a result of BfM participation. Although these findings diverge from the results in the present study, we do not discard their conclusions. Based on the above comparison, we suggest that the two most likely explanations for the diverging results are that changes took place in ordinary lessons rather than in BfM lessons, or that changes happened very early in the PD program.

Does duration matter?

The results from this study and the two most likely explanations for the diverging results compared to previous studies concern how, when, and to what extent change in instructional quality happens in PD programs. Specifically, the explanations may illuminate the significance of PD duration for PD effects, as well as how the effects of duration may be mediated by other PD features.

The present study and the comparison with previous BfM studies support the conclusion in reviews (Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019; Kennedy 2016; Kraft, Blazar, and Hogan 2018) that PD duration alone is not systematically linked to improved instruction and/or student achievement. Although earlier studies of BfM found small effects on instruction, the effects were not greater for teachers who had completed the program than for ongoing participants (Lindvall et al. 2021; Österholm et al. 2016). Along with the fact that the present study found no effect of PD duration, this indicates that the program could be shortened from a year to a few weeks without decreasing its effects on instructional quality. This raises questions about how teachers learn in the course of PD programs, and casts doubt on some existing claims.

Most existing frameworks of high-quality PD contend that programs should focus on the teaching of particular curricular content (e.g. Darling-Hammond, Hyler, and Gardner 2017; Desimone 2009). However, studies have failed to detect effects on student achievement from content-focused PD (Garet et al. 2016), or have found no difference in effects between programs with and without a content focus (Kraft, Blazar, and Hogan 2018). Indeed, the argument that mastering new ways of teaching subject matter requires substantial amounts of time and iterated opportunities for enactment and reflection (Darling-Hammond, Hyler, and Gardner 2017) can also be inverted to serve as an explanation for the lack of effect of PD duration. Thus, changing from typical mathematics instruction to ambitious mathematics instruction of adequate quality may be so complex that most teachers do not succeed or even neglect to attempt to do this. In fact, studies indicate that effects on student achievement are more likely when programs aspire to change procedural classroom behaviour than when they introduce complex teaching approaches (Desimone and Garet 2015). This argument is valid for BfM, as it advocated teaching approaches in line with ambitious mathematics instruction. If BfM initially inspired teachers to make superficial changes in their instruction but failed to bring about more profound changes over time, this would explain the demonstrated effects on instruction and the lack of discernable effects of duration.

Scholars have also attributed the lack of duration effects to difficulties in maintaining PD quality in long programs (Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019). The large scale at which the studied PD program was enacted likely further challenged the PD quality. In such programs it is difficult to achieve a high degree of competence among PD facilitators, content that is well-adapted to the target population, and satisfactory levels of motivation among participants (Murchan, Loxley, and Johnston 2009; Kraft, Blazar, and Hogan 2018). The standardised design of the BfM modules (including the teaching activities teachers were asked to enact) and the program’s use of local teachers as PD coaches exemplify this tendency.

In summary, the results of this study support claims in reviews that a broad and ambitious PD focus and inadequate PD quality may explain the absence of effects of PD duration (e.g. Basma and Savage 2018; Garrett, Citkowicz, and Williams 2019). In line with these claims, though, it is also possible that duration may increase PD effects in certain circumstances. Studies comparing PD programs, or variations of PD programs, for example, might investigate whether PD quality mediates the effects of duration in a substantial way. Studies could also investigate whether duration is important in certain forms of PD, such as programs in which teachers reflect on their practice using instructional quality guidelines (cf. Schoenfeld et al. 2019). Furthermore, although studies have indicated that PD advocating complex instructional strategies shows weaker effects (Basma and Savage 2018; Desimone and Garet 2015; Garrett, Citkowicz, and Williams 2019), there may exist methods for developing such instructional strategies. For example, the results from a recent study of a large-scale mathematics teacher PD program (O’meara and Faulkner 2022) suggest that PD workshops with concrete examples of pedagogical practices for mathematics teachers to conduct in the classroom led to significant improvements in mathematics teaching efficacy among participating teachers. Moreover, a review study (Kennedy 2016), as well as case studies of BfM (Insulander, Brehmer, and Ryve 2019; Van Steenbrugge et al. 2018), suggest that more prescriptive PD materials (e.g. suggesting certain teacher actions) to a greater extent support teachers’ in reflecting about and/or change their instructional practices than PD materials which rely on teachers drawing on their previous knowledge and making independent judgements. Perhaps ambitious mathematics instruction is best stimulated by providing teachers with detailed lesson plans that span over several weeks, so that the enactment of prescribed activities can be routinised into new habits? Until research has elucidated such questions, it may be wise for policymakers to carefully consider whether resources and teachers’ time are more effectively spent on ambitious and long-term PD programs, or on programs with narrow focal areas and shorter duration.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work was supported by the Swedish Research Council [Grant number 2014-2008].

Notes on contributors

Jannika Lindvall

Jannika Lindvall is a senior lecturer of mathematics education at Mälardalen University where she gained her doctorate in 2018. Her main research interest lies in teachers’ professional development and how to improve mathematics instruction at scale. ORCIDid: 0000-0003-2964-6297

Nils Kirsten

Nils Kirsten is a senior lecturer in special education at Stockholm University and also holds a position as researcher at Mälardalen University. His research interests include teachers’ professional development, teacher professionalism and educational governance. ORCIDid: 0000-0002-0218-3854

Kimmo Eriksson

Kimmo Eriksson is a professor of mathematics at Mälardalen University. He has a PhD in mathematics from the Royal Institute of Technology and a second PhD in social psychology from the University of Kent. His current research institutes include social norms, public opinion, and quantitative methodology in social science. ORCIDid: 0000-0002-7164-0924

Daniel Brehmer

Daniel Brehmer has a PhD in mathematics education and work as senior lecturer at Mälardalen university. His main research interests are educative curriculum materials and professional development for mathematics teachers. ORCIDid: 0000-0001-5259-2712

Andreas Ryve

Andreas Ryve is a professor of mathematics education at Mälardalen University and Östfold University College. The focus of his research is how to improve mathematics education at scale. ORCIDid: 0000-0002-3329-0177

Notes

1. While BfM also includes PD for principals and teachers in preschool and adult education, this study focuses on the PD program provided to teachers in Grades 1–9.

2. For descriptions and analysis of the PD materials, see Lindvall, Helenius, and Wiberg (2018).

3. For a full validity argument, we refer the reader to Appendix B.