Effect of Number of Locules, Loading Position, and Compression Speed on the Mechanical Behaviors of Tomato Fruits

Abstract

The mechanical properties of three or four half-ripe locular tomato fruits were characterized by compression testing at 0.5, 1.5, 2.5, 3.5 mm s⁻¹ to a final deformation of 4% using three loading positions. There was no significant dependence of any of the mechanical parameters on the loading position for these relatively low deformations. However, their dependence on the number of locules and compression speed was highly significant. It is clear that internal structural characteristics and the speed of compression need to be considered in investigations of tomato fruit mechanical behavior.

Keywords:

• Tomato fruit
• Number of locules
• Loading position
• Compression speed
• Mechanical behavior

INTRODUCTION

More than 150 million tons of tomatoes are produced annually.^[1] However, mechanical damage during harvesting, packaging, and transport represents a serious hazard to quality and has the potential to significantly reduce the value of the product.^[2] Mechanical damage can occur due to compression, impact, or puncture through fruit to fruit or fruit to equipment contact, the extent depends on the severity of the contact^[3] and the mechanical properties of the fruit.^[4] Therefore, some understanding of the latter is of great importance in food safety.

Arazuri et al.^[3] summarized the various mechanical tests to which tomato fruits might be subjected. These include compression tests, possibly to destruction of the fruit,^[5−10] puncture tests,^[11,12] impact tests, including drop tests,^[13−20] and hardness tests.^[3,21] In the present work, only compression testing was considered, which has particular relevance to robotic handling of fruit.^[8,22] Previous studies have assumed “quasistatic loading” in which inertial effects are presumed negligible and therefore, compressions were performed with only one compression speed (Arazuri et al.,^[3] 1 or 2 mm s⁻¹; Li et al.,^[6] 0.5 mm s⁻¹_; Li et al.,^[7,8] 1.5 mm s⁻¹; Albaloushi et al.,^[5] 1.5 mm s⁻¹). The compression speed during robotic harvesting is about 1.5 mm s⁻¹ or higher for harvesting efficiency.

In investigating the effects of compression speed on the mechanical behavior of tomato fruits, it is important to note that they have internal structure with three to eight locules.^[23,24] Therefore, three and four locule fruits were chosen respectively, representing fruits with an odd number of locules and an asymmetric internal structure and fruits having an even number of locules and a symmetric internal structure. In brief, the objective of this study was to understand the effect of number of locules, loading position, and compression speed on the mechanical behavior of tomato fruits.

MATERIALS AND METHODS

Material

Fenguan906 tomato fruits were grown at the Ruijing Vegetable Research Institute of Zhenjiang, China. Forty-three-locular tomatoes and 84-locular fruits were hand harvested in November 2010 at the light red ripening (half-ripe) stage according to USDA standards.^[25] Extremely large or small fruits were excluded at this stage. After being carefully transported within 3 h to the Key Laboratory of Modern Agricultural Equipment and Technology at Jiangsu University, China, the fruits were inspected to ensure that they were not damaged and not infected by worms. They were then placed randomly into 12 groups (60 samples) for subsequent experiments. The longitudinal height, maximum transverse diameter, and minimum transverse diameter of each fruit were measured with an electronic digital caliper to an accuracy of 0.01 mm and the geometric mean diameter, sphericity, and arithmetic mean diameter were calculated by the method given by Li et al.^[6] The fresh mass of each fruit was measured by an electronic balance to an accuracy of 0.01 g.

Compression Testing

Loading-unloading tests were performed by means of an electric vertical single column test stand (model AEL, Ali Instrument Co., Ltd., ZJ, China) equipped with a 100 mm diameter flat plate probe to compress a fruit against the base plate, as shown in Fig. 1. The initial distance between probe and the top point of a fruit was 10 mm and the final deformation was 4% of the original diameter in all experiments, which is typical of the deformations found using robot harvesting. Li et al.^[6] used deformations up to 20% but only at one speed.^[6] The time taken for loading to 4% final deformation was approximately 0.8 to 5.6 s.

FIGURE 1 Single column test stand (model AEL, Ali Instrument Co., Ltd., ZJ, China) equipped with a 100 mm diameter top plate to compress a fruit against a large base plate. The initial distance between the top plate and the top point of a fruit d was 10 mm. The figure indicates how three locular tomato fruits would be loaded by the top plate at position 1.

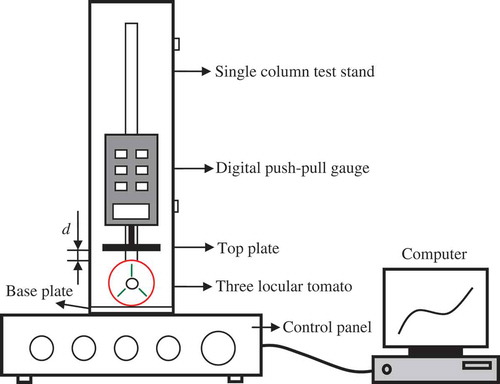
All compressions were across the equator of the fruit, each at one of three loading positions on the fruit surface, as shown in Fig. 2.^[7] Position 1 was with the top plate located over a cross wall of a three locule fruit. This was designated as T × CW but the three-fold symmetry of the internal structure implies that top plate compression at a cross wall requires locular tissue compression by the base plate, as can be seen in Fig. 2a. Position 2 was with compression by both plates over locular tissues of four locule fruits (F × L); and position 3 was with both plates compressing at cross-walls, also of four locule fruits (F × CW). A cross-wall could be identified visually by the valley position between two adjacent fruit shoulders.^[7] Four compression (loading) speeds (0.5, 1.5, 2.5, 3.5 mm s⁻¹) were used and 60 tomatoes (5 tomatoes × 4 compression speeds × 3 loading positions) were tested in a full factorial design experiment. Unloading was at the same speed as loading. An example force-displacement curve can be seen in Fig. 3a. The compression energy E_c, peak force F_max, and loading slope r_k were extracted from such curves using the method give by Li et al.^[6] Compression energy in this context is the internal stored energy of tomato throughout its volume as external loading deforms the fruit;^[26] the peak force is the maximum contact force between the plate probe and the fruit during compression; and the loading slope reflects the resistance of the fruit before its structure is broken down under compression. All compression tests were conducted at room temperature (15 ± 1°C: 63–65% relative humidity) within 24 h of arrival at the Key Laboratory of Modern Agricultural Equipment and Technology.

FIGURE 2 Three and four locular tomato fruits, (a) Three locular tomato fruit and its simplified equatorial section; (b) Four locular tomato fruit and its simplified equatorial section. Numbers 1, 2, and 3 represent loading positions 1, 2, and 3, respectively.

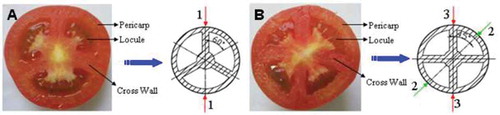
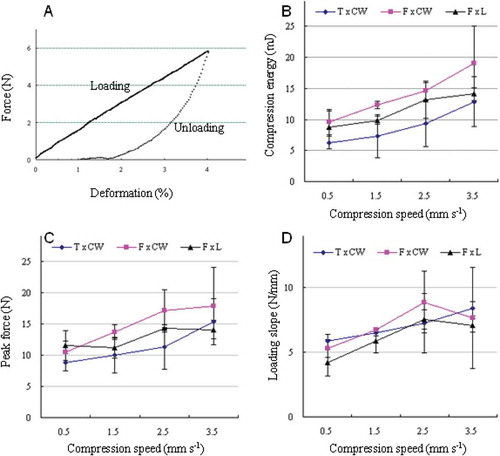
FIGURE 3 (a) Typical loading-unloading curve for compression of a three locular tomato fruits to 4% final deformation at a compression speed of 1.5 mm s⁻¹; (b) compression energy of tomato fruits at different loading positions for each compression speed; (c) peak force of tomato fruits at different loading positions for each compression speed; (d) loading slope of tomato fruits at different loading positions for each compression speed. T × CW: loading position over a cross wall of three locule fruits; F × L: loading position over locular tissue of four locule fruits; F × CW: loading position over a cross wall of four locule fruits. The error bars represent 95% confidence limits.

STATISTICAL ANALYSIS

Analysis of variance (ANOVA), simple correlation analysis, and multiple linear regression analysis were performed using SAS software, version 9.1.3 (SAS Institute Inc., Cary, NC, USA). The significance level was set at 0.05.

Multiple Linear Regressions

In multiple linear regressions, the compression energy E_c, peak force F_max, and loading slope r_k (the mechanical parameters) were considered as variables possibly dependent on the number locules (“locular number”), top loading position, compression speed, and the fruit geometry and mass. In the regressions, a dummy variable (LN) was used to express the locular number with three locule fruits coded as LN = 0 and four locule fruits as LN = 1. Because the loading positions were from fruits with different numbers of locules, it was not safe to include the position in the regressions, even as a dummy variable, so the effects of this variable were considered separately.

Regression Diagnostics

After multiple linear regressions, diagnostics were performed on the outcomes. A tolerance of 0.1 or less would indicate severe multicollinearity, i.e., the dependence of one of the presumed independent variables on any other. A white chi-squared test was used to detect any heteroscedasticity. A probability of less than 0.05 would indicate that the homoscedasticity assumption of the regressions was not met. A value of the Durbin-Watson D statistic of about two was used to indicate no significant first-order autocorrelation in the prediction errors from the regressions, which would mean the statistical tests on correlations might not be valid. After regression models had been established, correlations between the mechanical parameters were sought using a Pearson product-moment correlation coefficient matrix.

RESULTS

Loading-Unloading Test

Figure 3a shows that loading produced an essentially linear response of force to percentage deformation. Unloading showed that there was significant hysteresis and fruits did not return to their original height when the force was no longer applied. The implication is that structural damage had occurred during compression, which can also be observed directly.

Mechanical Behavior of Tomato Fruits

Fruit geometry and mass

The size, shape, and mass data are presented in Table 1, subdivided by compression speed, i.e., 15 tomatoes per speed. There were no significant differences between the means at the P = 0.05 level according to multivariate ANOVA which illustrates that the original four fruit groups were well-balanced. The size, shape, and mass of the fruits were not included in subsequent regression models.

Locular number, loading position, and compression speed

Figure 3b--d compares mean values of the mechanical parameters between locular number and loading position at each compression speed. Despite the apparent differences between F × CW and F × L, particularly for compression energy, no significant differences were found between the means at the P = 0.05 level. It could not be shown that loading position was a determinant of the mechanical parameters and therefore it was omitted from the subsequent regression analysis.

Regression models for dependence of the compression energy, peak force, and loading slope on locular number and compression speed, designated models 1 to 3, respectively, are presented in Table 2. The diagnostics showed homoscedasticity and no significant autocorrelation nor multicollinearity, and therefore, it was appropriate to evaluate the models overall by F tests and by t tests of the significance of each independent variable. The adjusted coefficients of determination R² were high suggesting all three models fitted the data well and it was concluded from F tests that the overall fits were significant. t tests showed that compression energy and peak force were dependent on locular number but the latter had no significant effect on the loading slope. Locular number was therefore excluded from the regression analysis for loading slope, while being included for the other mechanical properties.

TABLE 1 Size, shape, and mass of tomato fruits (mean value ± 95% confidence limits)

	Loading speed (mm s^−1)
	0.5	1.5	2.5	3.5	Overall
Number of fruits	15	15	15	15	60
Φ	0.87 ± 0.04	0.88 ± 0.02	0.83 ± 0.04	0.88 ± 0.03	0.87 ± 0.03
Dg (mm)	68.28 ± 2.69	68.16 ± 2.66	69.58 ± 5.31	71.71 ± 5.54	69.43 ± 4.05
Da (mm)	68.67 ± 2.76	68.44 ± 2.69	70.19 ± 5.31	70.05 ± 5.61	69.34 ± 4.09
M (g)	187.87 ± 22.77	179.47 ± 24.56	199.27 ± 21.04	192.52 ± 22.31	189.78 ± 22.67

Φ-sphericity, D_g-geometric mean diameter, D_a-arithmetic mean diameter, M-mass.

TABLE 2 Model 1, 2, and 3 with E_c, F_max, r_k as the dependent variable, respectively

Variable	Parameter estimate	t value	Probability > |t|	Tolerance
Model 1: Ec = β + α1 × CS + α2 × LN. Analysis of variance: F value: 25, Pr.: 0.0002, = 0.82
Intercept	β = 4.2	3.78	0.004
CS (mm s^−1)	α1 = 2.4	5.86	0.0002	1.00
LN	α2 = 3.9	4.09	0.003	1.00
Regression diagnostics: Chi-squared test: 4.07, Pr.: 0.40, Durbin-Watson D value: 2.15
Model 2: Fmax = β + α1 × CS + α2 × LN. Analysis of variance: F value: 21, Pr.: 0.0004, = 0.78
Intercept	β = 7.4	7.57	<0.0001
CS (mm s^−1)	α1 = 2.0	5.69	0.0003	1.00
LN	α2 = 2.5	3.05	0.01	1.00
Regression diagnostics: Chi-squared test: 3.70, Pr.: 0.45, Durbin-Watson D value: 2.183
Model 3: rk = β + α1 × CS. Analysis of variance: F value: 20, Pr.: 0.001, = 0.63
Intercept	β = 5.0	10.47	<0.0001
CS (mm s^−1)	α1 = 0.9	4.46	0.001	1.00
Regression diagnostics: Chi-squared test: 0.18, Pr.: 0.91, Durbin-Watson D value: 1.959

E_c: compression energy (mJ); F_max: peak force (N); r_k: loading slope (N m⁻¹); CS: compression speed (mm s⁻¹); LN: dummy variable for locular number was set at 0 for a three locule fruits and at 1 for a four locule fruits.

Correlations Between Mechanical Parameters

A Pearson correlation coefficient matrix between the mechanical parameters is presented in Table 3. This shows that there was a high positive linear correlation between experimental values of E_c and F_max (all fruits) but only a moderate correlation between E_c and r_k, and between F_max and r_k. Similar results were found by Sirisomboon et al. for tomato fruits,^[27] Polat et al. for nectarine fruit,^[28] and by Ahmadi for kiwi fruits.^[13] The implication of this is that compression energy (which is quite difficult to measure) could be predicted from the peak force (i.e., the force at 4% deformation) but not the loading slope.

TABLE 3 Pearson correlation coefficient matrix for the mechanical parameters

	Ec	Fmax	rk
Ec	1
Fmax	0.9541 (Probability < 0.0001)	1
rk	0.6436 (Probability = 0.024)	0.7366 (Probability = 0.0063)	1

E_c: compression energy (mJ); F_max: peak force (N); r_k: loading slope (N m⁻¹).

DISCUSSION

Effect of Loading Position, Locular Number, and Compression Speed

Top loading position

In this compression test, there was no significant dependence of any of the mechanical parameters on the loading position for a final deformation of 4%. Although such deformations might be considered relatively low, they are typical of those used in robot harvesting. In contrast, it is known that loading position is important when the compression level is relatively high and that tomato fruits are susceptible to rupture when the compression level is more than 12%.^[6] Therefore, Li^[9] proposed that the rupture probability of four locule tomato fruits was highest when they were loaded at the cross-wall tissues, and the odds of being ruptured were 14.5 times higher for four locule tomato fruits loaded at the cross-wall tissues compared to the locular tissues, when all other variables were constant. For impact studies on tomato fruits, Van Linden et al.^[18] proposed that impact energy was the most important explanatory variable for the incidence of bruise damage but also that the second explanatory variable was impact position (without considering the number of locules). Possibly the number of locules masks changes due to loading position. More extensive studies demonstrate loading position effects. Actually this variable is controllable by computer vision under field conditions, especially in robot harvesting, therefore, this knowledge could affect harvesting practices.

Locular number

According to the regression models (Table 2), the compression energy and peak force increased significantly between four and three locule tomato fruits (all compression speeds) although no effect on loading slope could be demonstrated. In general, these results show that the internal structure of the fruit is important in compression testing and should be taken into account in testing protocols. The resistance to deformation (and therefore, the compression energy and peak force) would appear to be a combined effect of structural and local deformations. This is supported by the typical data in Fig. 3a which shows some elastic recovery on unloading, which would be expected if there were structural deformations. The differences between three and four locule fruits may reflect a more generic difference between fruits with odd and even numbers of locules but this was not tested directly here.

It should be noted that compression energies are not intrinsic mechanical properties of fruits as they depend on the final deformation. Nevertheless, they are useful for comparisons between cultivars and a final deformation of 4% is appropriate for robotic harvesting. The values found in this work were much lower than the rupture energies of similar cultivars found by Li et al.^[8] This is unsurprising as the deformations in that work were about 15%, causing severe damage to the fruit structure. It has been shown that the peak force is important in determining mechanical damage of fruit. For example, relationships between bruise volume of apple and pear fruits and peak force have been shown by Van Zeebroeck et al.^[20] and Wu et al.^[29] Again regression analysis (Table 2) showed a highly significant dependence of peak force on the internal structure of the fruits.

Compression speed

According to the regression models (Table 2), the compression energy and peak force increased on average by 3.9 mJ and 2.5 N, respectively, when four locule tomato fruits were compared with those with three locules (all compression speeds). Compression speed also had a significant effect on the compression energy, peak force and loading slope with these increasing on average by 2.4 mJ, 2.0 N, and 0.9 N mm⁻¹, respectively, for each 1 mm s⁻¹ speed increase. The changes with either or both locular number and compression speed were large compared to the values at any given speed. For example, with three locule fruits and a compression speed of 1.5 mm s⁻¹, the mean values were 7 ± 3 mJ, 10 ± 3 N, and 6.5 ± 0.2 N mm⁻¹, respectively (five tomato fruits in each case).

Similar increases in these mechanical parameters with increasing compression speed have been found by Bajema et al. and Aregawi et al. on apple fruits,^[30,31] Kilickan and Guner on olive fruits,^[32] and Altuntas and Erkol on walnut cultivars.^[2] These results suggest that the quasistatic assumption may not be valid for such compression tests, which occur over timescales of seconds. It is not clear which time-dependent effects are most important, although some researchers have proposed that fruits and their tissues are viscoelastic.^[31,33] In any case, it is clear that the speed of compression tests needs to be standardized in investigations of tomato fruit mechanical behavior. As the compression energy and peak force increase with compression speed, it may be worthwhile to reconsider the speed at which fruits are grasped during robotic handling, in order to reduce any damage.

CONCLUSIONS

The mechanical behavior of three and four locular tomato fruits at the light red ripening stage has been investigated under different compression speeds and at three loading positions (cross-walls of three locule fruits, locular tissues, and cross-walls of four locule fruits). The mechanical parameters depended significantly on both the locular number and the compression speed. The latter undermines the usual quasistatic assumption and suggests lower speed grasping during robot harvesting may be effective in reducing damage to the fruits. No significant dependence of the compression energy, peak force, and loading slope on the loading position could be demonstrated. The compression energy and peak force increased on average by 3.9 mJ and 2.5 N, respectively, when four locule tomato fruits were compared with those with three locules. For each 1 mm s⁻¹ speed increase, the compression energy, peak force, and loading slope increased on average by 2.4 mJ, 2.0 N, and 0.9 N mm⁻¹, respectively. These changes were large compared to the values at any given speed. It is clear that the internal structural characteristic of fruit and the speed of a compression test need to be considered in investigations of tomato fruit mechanical behavior and there might be implications for fruit handling and texture assessment.

FUNDING

This work was supported by a Marie Curie International Incoming Fellowship within the 7th European Community Framework Program (326847 and 912847) and the National Natural Science Foundation of China (U1204107 and 11310101008).

Additional information

Funding

This work was supported by a Marie Curie International Incoming Fellowship within the 7th European Community Framework Program (326847 and 912847) and the National Natural Science Foundation of China (U1204107 and 11310101008).