Between expert and student perspectives: on the intersection of affect and heuristic-didactic discourse in the undergraduate classroom

ABSTRACT

This paper explores student emotion and learning experiences fostered by lecturing-style instruction in Real-Analysis problem-centered lessons. We focus on two lessons that were taught by two reputable instructors and involved challenging, mathematically-related problems the students did not understand. Nonetheless, one lesson evoked negative emotional reactions, while the other positive emotional reactions – a phenomenon we aimed at explaining. The main data comprise the filmed lessons and subsequent stimulated-recall interviews with nine students. The analysis draws on conceptual tools from three perspectives: mathematical discourse, variation theory, and a recently developed construct of key memorable events (KMEs) that offers an affective-cognitive lens for investigating the interrelation between teaching and learning. The findings indicate that the positively-perceived lesson contained instances of what we call heuristic-didactic discourse: a meta-level discourse that presents heuristics monitored from an expert’s perspective, yet derived from a student’s perspective. Implications for research and practice are drawn.

KEYWORDS:

• Affect
• emotions
• key memorable events
• meta-level discourse
• learning affordances
• real analysis
• undergraduate mathematics education
• double Riemann integral

Introduction

In recent years, undergraduate mathematics education has become an emerging field in mathematics education research, necessitating the development of theoretical and practical perspectives to address the teaching and learning of tertiary mathematics (Nardi & Winsløw, 2018; Viirman, 2015). In this paper, we report on part of a wider study (Marmur, 2017, 2019; Marmur & Koichu, 2016) aimed at investigating the instructor’s role in shaping undergraduate-students’ learning of problem solving in a large-size classroom environment (see also Lester, 2013). Our research approach is in line with a growing body of studies that do not make a dichotomous separation between teaching and learning, but rather put emphasis on the communicational and social setting of the mathematics classroom, and examine the learning in the context of the teaching that takes place (Nardi et al., 2014).

Within this approach, we utilize mathematical affect as our lens, and examine undergraduate teaching and learning while considering students’ experienced mathematics-related emotions. Emotions have long been recognized to take an integral part in mathematics learning, especially during non-routine problem solving and when situated in a social context of a classroom environment (e.g., McLeod & Adams, 1989; Op’t Eynde et al., 2006; Zan et al., 2006). However, as Hannula (2012) remarks, studies on students’ emotional or motivational states tend to focus on individuals, while less research has been done on affective states and their relation to learning in the context of a classroom. While this observation regards all levels of education, we note that even less is known on the role of emotions in student learning during undergraduate mathematics lessons (Marmur, 2019; Martínez-Sierra & García-González, 2016).

Accordingly, our study aims at shedding light on the complex relationship between student emotion and learning as shaped by lecture-based instruction in large-size undergraduate mathematics lessons. More specifically – and considering the dominant role of the instructor as the leader of discourse in the undergraduate classroom – we aim to gain a better understanding of how affective experiences of students are shaped by the instructor’s discursive acts, and what learning affordances are associated with these affective experiences. The suggested interrelationship between discourse and emotion has been recently acknowledged in mathematics education research, where studies stemming from sociocultural perspectives have conceptualized emotions as socially organized phenomena that are rooted in discourse (e.g., Evans et al., 2006; Heyd-Metzuyanim & Sfard, 2012; Sinclair & Heyd-Metzuyanim, 2014; Turner et al., 2002). Therefore, we believe that examining students’ mathematics-related emotions in particular relation to the instructor’s mathematical discourse can provide insight into students’ learning processes in the lecture-based classroom.

In this paper, we focus on two Real-Analysis lessons involving challenging, mathematically-related problems that the participating students claimed they did not understand when asked in follow-up interviews – yet the learning experience in each lesson was consistently described by the students in opposite emotional terms. In one of these lessons (henceforth referred to as Lesson-N), the students’ lack of understanding of the solution was accompanied by negative emotions of anger and frustration, whereas the other lesson – and initially much to our surprise – was regarded by students as a positive learning experience (henceforth referred to as Lesson-P).¹ Juxtaposing the two lessons, we were wondering what underlying reasons could account for the positive lesson descriptions given by the students of Lesson-P, who nonetheless described key parts of the proof as incomprehensible and showed disbelief in their ability to solve such a problem on their own. To inquire into this phenomenon, we examine not only Lesson-P but also Lesson-N as a contrastive background providing a supporting angle to the interpretation of the findings. Our analysis utilized a discursive perspective on the teaching and learning of mathematics, as well as a recently developed construct of key memorable events (KMEs) that offers an affective-cognitive lens for investigating the interrelation between teaching and learning (Marmur, 2019).² The findings indicate that the students in Lesson-P highly valued a certain kind of meta-level discourse initiated by the instructor, which in the Discussion section we conceptualize as heuristic-didactic discourse.

Theoretical underpinnings

Instructor discourse and learning affordances in the lecture-based classroom

In many universities worldwide, including the one where this research took place, undergraduate mathematics courses continue to be taught in a lecture style. This common teaching style has been heavily criticized due to the one-directional, non-responsive mode of communication and interaction it promotes (e.g., Alsina, 2002; Cooper & Robinson, 2000). It has been argued that the lecture method is focused on transmitting information (Biggs & Tang, 2011), does not allow significant student feedback, and does not promote independent thought (Bligh, 1972). Nonetheless, there have also been claims made on the advantages of lecturing in the context of undergraduate studies (e.g., Bergsten, 2007; Rodd, 2003; Sfard, 2014). For example, there is evidence this teaching method can be effective in modeling mathematical reasoning for students, particularly when exposing the struggle that precedes the reaching of a solution (Pritchard, 2010). It is not our intention to either support or oppose these claims. Rather, we take a pragmatic approach and recognize this traditional teaching method remains to be widespread, not prone to change, and will most likely not disappear in the near future (Cooper & Robinson, 2000; Nardi et al., 2005; Yoon et al., 2011). Accordingly, we argue for research efforts to be put into understanding and improving the existing university system of teaching from within, both theoretically and practically.

Considering the relatively passive role of students during undergraduate lectures (Cooper & Robinson, 2000), one may wonder what or how students manage to learn in such lessons. Indeed, research into learning that occurs during undergraduate-mathematics lecture-based lessons entails both practical and theoretical difficulties. From a practical perspective, the lecturing style of undergraduate lessons typically implies the instructor to talk most of the time, whilst the students are writing in their notebooks and occasionally engage in asking questions. Without being able to read students’ minds, the observation of university mathematics lessons provides very few indicators of how students construct meaning, develop understanding, and advance their proving and problem-solving skills during such lessons. From a theoretical perspective, a substantial part of the learning may not even be expected to occur in real-time during a lesson. High-level complex mathematics at university requires a lengthy and continual process of self-engagement with the material in order to successfully and deeply construct meaning and reasoning, a process that can ultimately only occur when a student works independently “in the quiet of her room” (Sfard, 2014, p. 202). Therefore, the university lecture-based lesson serves as a necessary, yet only initial stage of the learning process.

Consequently, when studying learning in undergraduate mathematics lessons in the context of our research, we borrow ideas from variation theory (e.g., Marton & Booth, 1997; Runesson, 2005); and rather than attempting to determine what is learned, we examine what is possible to be learned – that is, the affordances for student learning the classroom situation provides. To elaborate, variation theory approaches the general question “what do students learn?” through three complementary angles: a) what is intended to be learned? (referred to as the intended object of learning); b) what is possible to learn? (the enacted object of learning); and c) what is learned? (the lived object of learning) (Runesson, 2005). Based on the aforementioned practical and theoretical considerations on how to investigate real-time classroom learning, we focus on the enacted object of learning and attend to the learning affordances available to the students in a particular classroom setting. This is in line with our approach of examining learning in the context of the situation in which it occurs, as the enacted object of learning is “co-constituted in the interaction between learners and the teacher or between the learners themselves” (Runesson, 2005, p. 70).

Furthermore, considering that learning is shaped through communication even in a lecture-based classroom setting, we utilize here a discursive perspective to examine what affordances for student learning might exist. In accord with Sfard and Kieran (2001), we use the notion discourse as “any specific instance of communicating, whether diachronic or synchronic, whether with others or with oneself, whether predominantly verbal or with the help of any other symbolic system” (p. 47). Recognizing the situational interrelation between cognition and affect during mathematics learning (Zan et al., 2006), we regard mathematical discourse as incorporating emotional, social, and pedagogical aspects of the discourse held within the mathematics classroom; and in line with Heyd-Metzuyanim and Sfard (2012), we view “cognition, affect and social matters as aspects of the discourse that takes place when people learn mathematics” (p. 129).

When examining classroom discourse, we may attend to the discourse between instructor and students as a whole, the discourse of students only, or the discursive acts of the instructor. Considering the lecture-based norms of the undergraduate classroom, where the instructor serves as the leader of mathematical discourse and student oral-participation is minimal, we concentrate on the instructor’s discourse and how it may shape students’ learning. The focus on the instructor’s discursive acts finds support in studies from recent years (e.g., Park, 2015; Pinto, 2019; Viirman, 2015), which analyze the discourse of university mathematics teaching utilizing constructs offered by Sfard’s (2008) commognition theory. Indeed, the commognition approach to discourse offers an (almost) synonymous view on the concepts of thinking and (self) discourse, which is pertinent when analyzing the instructor’s predominant role in the lecture-based classroom. If we regard “thinking” as “private discourse” (see also Harré & Gillett, 1994), then we may treat the monologic nature of the instructor’s discourse as a public enactment of her private thinking process. This “uncovering” of the instructor’s thinking process consequently offers an affordance for student learning. Sfard (2014) suggests that as formal undergraduate mathematics requires a shift in students’ mathematical way of thinking (see similar claims made by Tall, 1992), a preliminary condition for undergraduate mathematics learning is a student’s exposure to a discourse held by an expert-mathematician.

As our study is situated in undergraduate mathematics lessons involving problem-solving activities, we note that the discourse of problem solving may shift between a “straightforward” discourse-mode focused on the mathematical objects involved in the problem; and what could be referred to as a “meta-level discourse,” which reflects on the approaches and strategies taken to deal with the problem. The notion of a meta-level discourse can be found in varying forms in the work of different researchers. Cobb et al. (1997) established the term reflective discourse as a discourse “in which mathematic activity is objectified and becomes an explicit topic of conversation” (p. 258). Similarly, Rogalski (2000) focused on the meta-discourse of the teacher as a means to evoke a reflexive mode of thinking in students on their mathematical activity. Sfard (2008) referred to a meta-level discourse as a “discourse about another (object-level) discourse” (p. 299). Considering learning as a change in discourse, Sfard further distinguished between object-level learning, which expands the existing discourse (in what Sfard refers to as words, routines, and endorsed narratives); and meta-level learning, which involves a change in the meta-rules of the discourse. Meta-rules of a discourse “speak about the actions of the discursants, not about the behavior of mathematical objects” (Sfard, 2008, p. 201); that is, they define patterns in the discursants’ activity when engaging in object-level discourse. In relation to our study, a change in the meta-rules of the discourse might mean that a familiar task such as solving a problem, will now be done in a new and unfamiliar way.

As opposed to discursive approaches that require the meta-level discourse which objectifies another mathematical discourse to be made explicit to students (e.g., Cobb et al., 1997), this is not a defining prerequisite according to Sfard’s framework (e.g., as demonstrated in the work of Güçler, 2013, 2016). This implies that also when the meta-rules of the discourse remain implicit, the instructors’ “recurrent actions and their comments about their actions, provide glimpses into their mathematical discourse and its underlying meta-rules” (Pinto, 2019, p. 4). Accordingly, since a change in the meta-rules of the discourse is not likely to be initiated by students (Sfard, 2008), the instructor’s mathematical discourse serves a crucial role in creating affordances for students’ meta-level learning.

Linking this back to our previous discussion on variation theory and the considerations involved in investigating learning that occurs during undergraduate lessons, we recall that rather than inquiring into the lived object of learning, we focus on the enacted object of learning, meaning, the learning affordances available to the students through the instructor’s discourse. Accordingly, we combine notions from different theoretical frameworks and in this study attend to meta-level learning affordances (and object-level learning affordances) that are shaped by the instructor’s discursive acts. That is, building on the concepts “object of learning” from variation theory (Marton & Booth, 1997; Runesson, 2005) and “discursive meta-rule” from a discourse perspective (Sfard, 2008), the term “meta-level learning affordance” views the enacted object of learning as a change in the meta-rules of the discourse.

The next section presents an additional theoretical framework for examining students’ learning processes, which stems from an affective-cognitive representational perspective (Goldin, 2000; Marmur, 2019). We acknowledge that the act of taking elements from different theoretical frameworks and combining them together could present a risk to the theoretical compatibility and coherence, particularly in regard to the nature of mathematical thought. According to the representational perspective, mathematical thinking is conceptualized in terms of internal systems of representation, where affect is one such system; each system is here regarded as encoding meaning for the individual, where this meaning may be externalized when communicating with others (DeBellis & Goldin, 2006). Contrastingly, according to a discursive perspective, discourse is not regarded as an external representation, but rather as synonymous to the thinking itself; rather than inferring the invisible (e.g., cognition) from the observable (e.g., speech), discourse research attempts to directly examine the discursants’ patterns of communication and how these develop over time (Kieran, 2001; Sfard, 2008).

Nonetheless, as our study is situated at the intersection of several interrelationships (i.e., teaching-learning-discourse-emotion), combining theoretical approaches as suggested by Prediger et al. (2008) may offer ways to bridge between these multi-faceted interrelationships. Accordingly, we suggest that some theoretical incompatibility is perhaps not only inevitable, but may also contribute and lead to new insights. As argued by Prediger et al. (2008): “Combining theoretical approaches does not necessitate the complementarity or even the complete coherence of the theoretical approaches in view. Even theories with conflicting basic assumptions can be combined in order to get a multi-faceted insight into the empirical phenomenon in view” (p. 173). Specifically, in this paper we examine the instructors’ discursive rules from the students’ affective perspective. As will later be demonstrated, it is through the combining of the three theoretical perspectives (i.e., discourse, affect, and variation theory) that we were able to observe and identify a discursive-affective phenomenon associated with meta-level affordances for learning (which we later refer to as “heuristic-didactic discourse”).

Students’ emotional states in the lecture-based classroom

One of the criticisms of university lectures is that this teaching style promotes the treatment of students as a “non-emotional audience” (Alsina, 2002, p. 6), while granting them no room for personality differences, individual problems, or emotional difficulties. Nonetheless, studies have shown it is possible to attend to students’ affective needs in lectures as well, and have characterized this as part of what high-quality university-teaching entails (e.g., Bergsten, 2007; Jaworski, 2002; Marmur & Koichu, 2016; Movshovitz-Hadar & Hazzan, 2004). This observation requires follow-up research that examines in depth the ways in which students’ emotions play a role in their learning processes during mathematics lectures.

In the past several decades, research in mathematics education has increasingly examined the role of affect in mathematics learning, such as the impact of students’ beliefs and attitudes toward the subject on their mathematical achievements (e.g., Hannula, 2015; McLeod, 1992), or the role of students’ self-regulation of emotions in attempting to solve challenging problems (e.g., Goldin, 2000; Hannula, 2006). However, relatively little research has addressed the role affect plays in the undergraduate mathematics classroom (Marmur, 2019; Martínez-Sierra & García-González, 2016). Moreover, within research on mathematical affect in tertiary studies, more attention has been given to the steady traits of students’ beliefs and attitudes toward mathematics (e.g., Alcock & Simpson, 2004; Hernandez-Martinez et al., 2011; Szydlik, 2000), while relatively little has been reported on students’ real-time emotions and the ways in which these relate to their learning during a lesson (e.g., Goldin, 2014).

Students’ experienced emotions during problem-solving activities may vary substantially. These might include, for example, feelings of frustration, anxiety, anger, relief, happiness, pleasure, curiosity, puzzlement, or perplexity (Goldin, 2000; Gómez-Chacón, 2017; Op’t Eynde et al., 2006). Such in-the-moment emotions accompany a range of problem-solving heuristics and at different times might be experienced by any student: both by students who possess negative beliefs and attitudes toward mathematics, as well as by those who possess positive ones. Especially during challenging problem-solving activities, all students, regardless of their mathematical inclinations, may experience negative emotions such as anger, fear, and threat to their self-efficacy. However, students’ self-regulation of emotions when engaged in such activities can play a defining role in how successful they ultimately are in their attempts to solve a problem (Goldin, 2000; Hannula, 2006; Malmivuori, 2006).

Concerning student emotions in undergraduate mathematics lessons, the relatively few studies on this subject have highlighted the influence of situational conditions on students’ experienced emotions. For example, Martínez-Sierra and García-González’s (2016) study inquired into students’ emotional experiences in Linear Algebra courses, which included emotions of satisfaction, though also emotions of disappointment, distress, and self-reproach. Utilizing appraisal theories of emotion (e.g., Moors et al., 2013), the study showed how students’ emotions were triggered by the students’ appraisal of different classroom situations (e.g., asking questions or solving problems on the board) in terms of specific achievement goals. In another study, Marmur and Koichu (2016) illustrated how the same Real-Analysis problem elicited vastly different student emotions, depending on the way in which it was taught. Whereas early iterations of how the problem was taught evoked emotions of anger and threat to students’ self-efficacy, later iterations of the lesson succeeded in evoking the opposite: emotions of enjoyment, excitement, and rise in self-confidence.

In order to theoretically address students’ learning experiences during undergraduate lessons in the context of this paper, we utilize the notion of key memorable events (Marmur, 2019), which has been developed as an expansion of Goldin’s (2000, 2014) framework of local affect. Goldin (2000) views local affect as contextually-rooted emotions that take part while engaging in mathematical problem-solving activities; and defines emotional states as “the rapidly changing (and possibly very subtle) states of feeling that occur during problem solving” (p. 210). While attitudes and beliefs are relatively stable attributes of affect, emotions, referred to by Goldin as “emotional states,” are not. Rather, they are constantly changing, context dependent, local states, that may range from mild to intense, as well as be conscious or subconscious (DeBellis & Goldin, 2006). Emphasizing this differentiation from a complementary perspective, Goldin et al. (2011) distinguish between students’ traits and states, where traits are longer-term and more stable characteristics of individuals, and states (i.e., emotional states) are changing emotions relating to in-the-moment mathematical behavior.

Acknowledging the changing and evolving nature of student emotions during mathematical activity, Goldin (2000) refers to a sequence of emotional states as an affective pathway. These pathways are not set and regarded solely in the affective domain, but are linked to mathematical cognition and heuristic processes students utilize at different stages of mathematical problem solving. Accordingly, emotional states on their own are neither “good” nor “bad,” as their meaning depends on the role they play within an affective pathway of a problem-solving activity. For instance, an emotional state of frustration may play a crucial role in a student’s affective pathway, leading to either negative or positive outcomes: frustration coming from not knowing how to progress in a solution may be perceived as anticipation of failure, leading to subsequent anxiety and despair; however, when frustration is followed by success (even partial), it may lead to enhanced feelings of encouragement and self-pride of managing to overcome a challenging mathematical task (Goldin, 2000; Goldin et al., 2011). The above example additionally points to a more general phenomenon: not all emotional states in affective pathways are of equal significance, and some may be more meaningful than others (Marmur, 2019). Indeed, recent studies have illustrated the presence of “key moments” in students’ learning pathways; for example, by providing evidence that even a single strongly positive mathematical experience may have a considerable effect on a student’s success, engagement with the material, and attitude toward the subject (e.g., Liljedahl, 2005; Marmur & Koichu, 2016; Weber, 2008).

Addressing the above phenomenon, Marmur (2019) has pointed to the widely-acknowledged interconnection between memory, emotion, and learning (e.g., Hinton et al., 2008; LaBar & Cabeza, 2006; Wolfe, 2006), and accordingly suggested focusing on the memorability aspect of experienced emotions and the associated events that triggered those. Marmur regards memorable events “not merely as events that can be recalled from memory upon request, but as events that additionally hold significance and meaning for a person who experienced them” (p. 4). However, an event that is memorable to one student, may not be memorable nor significant to another. Consequently, Marmur defines Key Memorable Events (KMEs) as those events that are “perceived by many students in class as memorable and meaningful in support of their learning, and are typically accompanied by strong emotions, either positive or negative” (p. 1).³ In other words, KMEs, which are events of both affective and cognitive nature, are situated in the social domain as memorable experiences with shared meaning.

Due to the complexity of emotions involved in classroom mathematical activities, we suggest the learning affordances that students are able to experience in a lesson are influenced by their emotional states during the course of the lesson. For example, one may imagine that when a student is feeling mathematically frustrated or insecure when attempting to understand a problem, then he or she may be less “open” to gain any possible learning affordances that are available to him/her at that moment in time. Accordingly, attending to the affective dimension of student learning provides insight into what is possible to be learned in a particular teaching-learning interaction (see also Heyd-Metzuyanim & Sfard, 2012).

In this paper, we use the concept of KMEs as a lens through which to focus on meaningful classroom events and their role in student learning. In particular, we suggest that students’ emotionally-loaded experiences shaped by an instructor’s discourse, may point toward affordances for a discourse change, which accordingly provides affordances for learning.

Utilizing the above framework, we have taken a student-centered approach in our study and formulated the following research questions to guide our investigation:

• What are undergraduate Real-Analysis lesson-events that serve as KMEs for students, and how are these events shaped by the instructor’s discourse according to the student perspective?

• What are the enacted and/or missed learning affordances associated with the instructor’s discourse during these KMEs according to the student perspective?

Method

Context, participants, and problems of interest

The research took place in a first-year undergraduate Real-Analysis course attended by computer-science and electrical-engineering students in a highly-ranked research university in Israel. The course comprised both theory-centered lectures where the lecturer presented definitions, theorems, and proofs, as well as problem-centered lessons in which the instructors presented and solved problems in a traditional lecturing style. The main data were collected in regard to eight problem-centered lessons and consist of 36 stimulated-recall interviews with individual students who volunteered to be included in the study (Marmur, 2017). For this paper, we focus on two lessons, each involving a similarly challenging and related problem that the participating students did not understand, yet responded to with opposite emotional reactions. The lessons will be referred to as Lesson-P and Lesson-N for ease of reading, corresponding to the student accounts of their positive/negative learning experiences. While our main focus is on Lesson-P, we utilize the juxtaposition with the related Lesson-N to which students responded oppositely, to help us discern and analyze those aspects in the instructors’ discourse leading to different learning experiences of students.

Lesson-N and Lesson-P refer to two different two-hour problem-centered lessons attended by approximately 50 students each. The lessons were part of a Real-Analysis 2 course and were taught by two different instructors during the same semester. The problem of interest in each lesson was based on the “popcorn function” (also known as Thomae’s function⁴). Both problems required the use of the definition of a Riemann-integrable function – Lesson-N addressed the one-variable case and Lesson-P the two-variable case. The problems are presented below according to the chronological order in which they appeared in the semester. Both instructors (henceforth referred to as Instructor-N and Instructor-P) had more than ten years of teaching experience in Calculus and Real-Analysis courses and a reputation among peers and students for being excellent instructors (including multiple teaching awards). In choosing the problems for our study, we informed the instructors of our intent to inquire into the interrelationship between affect and learning. Accordingly, they suggested the aforementioned problems based on the “popcorn function” as they regarded these problems as exceptionally challenging and suspected these would likely evoke strong emotional responses in students.

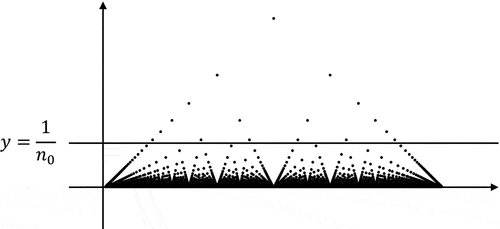
In Lesson-N, which took place during the first half of the semester, the problem of interest was to prove that the “popcorn function” (see also Figure 1)

$f\left(x\right)=\left\{\begin{array}{cc}\frac{1}{q}& x=\frac{p}{q}\in \mathbb{Q},\frac{p}{q}\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{s},q>0\\ 0& x\notin \mathbb{Q}\end{array}\right.$

Figure 1. The graph of the popcorn function on (0,1).⁵

is Riemann integrable on $\left[0,1\right]$ (and the value of the integral is 0).

In Lesson-P, which took place during the second half of the semester, the students were asked to prove that the function

$f\left(x,y\right)=\left\{\begin{array}{cc}\frac{1}{q}& x\in \mathbb{Q}\mathrm{a}\mathrm{n}\mathrm{d}y=\frac{p}{q}\in \mathbb{Q},\frac{p}{q}\mathrm{i}\mathrm{n}\mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{s},q>0\\ 0& x\notin \mathbb{Q}\mathrm{o}\mathrm{r}y\notin \mathbb{Q}\end{array}\right.$

is Riemann integrable in two variables on $\left[0,1\left]\times \right[0,1\right]$ (and the value of the integral is 0).

Similar to Instructor-N, Instructor-P had also taught the problem with the one-variable popcorn function earlier in the semester. In the current lesson, Instructor-P planned the above follow-up two-variable version of the popcorn function.

Data collection

The data collection consisted of filming the lessons, observing them in real-time (whilst taking observation notes), and conducting individual stimulated-recall interviews with volunteering students in the immediate days following the lessons. Additionally, we held recorded conversations with the instructors providing context for the lessons, and made photocopies of the lesson-notes that were taken by the interviewed students during the lessons. The stimulated-recall methodology was chosen as the main source of data collection as it aids students in reexperiencing a lesson and consequently provides insight into the students’ thought-process during its course (Calderhead, 1981; Pirie, 1996).

The stimulated-recall interviews on Lesson-P and Lesson-N were conducted with nine volunteering students: five students from Lesson-P and four from Lesson-N, where each student participated in only one of the two lessons. At the beginning of the interview, the students were given explanations on its general goal (i.e., an inquiry into student learning during problem-centered lessons), how it would be conducted, and what lesson and problem it would focus on. This provided the students an opportunity to unsolicitedly share their memories, thoughts, and emotions regarding the problem or entire lesson, if they so chose to, as was typically the case.

Subsequently, the students were presented with a 20-minute filmed excerpt of the lesson containing the problem of interest, which they watched with their lesson-notes in front of them to anchor their recollection of the events (see Weinberg et al., 2014, for a similar approach to stimulated-recall interviews on mathematics lectures). The students were asked to stop the playback whenever they recalled what they thought or felt at that moment, and were told that if they did not stop the playback for an extended period of time, the interviewer (the first author of this paper) might stop it occasionally and ask them whether they had any recollections on that specific moment (in practice, there was barely any need to implement this type of intervention). When students stopped the video to share their memory of an event, they were often asked clarifying questions, mainly in the form of: “can you explain why you thought/felt this way at that moment?” At the end of the interview, the students were asked follow-up questions regarding themes that came up during earlier stages of the interview, as well as questions about their attitude toward the lesson and the subject in general.

Considering the planned interview structure as described above, we had decided to follow Shkedi’s (2003) methodological recommendation to care for the participants’ well-being by limiting the length of the interviews so these would hopefully not be too lengthy and tedious for the participants. Accordingly, we confined the viewing of the videos to 20-minute excerpts that included most of the discussion of the problems, as we believed this was sufficiently long to enable the students to recall details from their classroom experience (see Appendices A and B for a detailed description of the parts of the lessons that were shown to the students). The interviews ranged in length from 40 to 65 minutes, depending on the level of detail shared by the student. The interviews were audio-recorded and transcribed in their original language (Hebrew), and parts of these transcriptions were subsequently translated into English for presenting the data in this paper.

Data analysis

During the analysis process we utilized a general inductive approach (Thomas, 2006), as this methodology supports the coordination of extensive data into a brief summary that addresses the “underlying structure of experiences or processes” (p. 238) most apparent in the data. The analysis consisted of the following stages: (a) Dividing each filmed lesson into a list of consecutive events over time, based on observable actions (e.g., a student asks a question, the instructor provides an answer, the instructor writes the explanation on the board), and continuously refining the list based on the students’ accounts; (b) Identifying memorable events for each student based on unsolicited details provided on thoughts or feelings in regard to an event; and (c) Identifying key memorable events (KMEs) and examining their associated learning affordances. In the identification process of KMEs, we first concentrated on those events that were addressed with a common theme by all interviewed students, with the exception of one at most. Within these, we looked for those events where strong student emotion could be inferred (e.g., statements such as “I loved/hated this,” “it was beautiful/horrible”). Additionally, we looked for the students’ use of intensifying adverbs (e.g., “I really loved it”) and repeated unsolicited statements on the event throughout the interview (e.g., before, during, and after watching the event).

Subsequently, we examined how the identified KMEs shaped the students’ learning experience in class, as well as the enacted/missed learning affordances associated with the instructor’s discourse during these events. In line with our student-centered approach, rather than directly investigating the instructors’ discourse, we inquired into the students’ perspective on their instructor’s discursive meta-rules (i.e., the patterns and regularities in the instructor’s discursive acts). In certain cases, the identification of the discursive meta-rules was based on students explicitly referring to utterances made by their instructor, while providing the meaning they attributed to these. In other cases – since instructors do not usually discuss the meta-rules of their discourse in an explicit manner in class (Pinto, 2019) – the identification of the discursive meta-rules was made in a more indirect manner through the students’ interpretations of their instructor’s comments and actions. Especially in such cases, we looked for additional perspectives in the data in support of the students’ interpretation, such as pre- and post-communications with the instructors, or observations we made of instructor utterances. If the students expressed positive emotions alongside learning affordances in regard to their instructor’s discursive acts, we interpreted this as a discursive meta-rule the students wished to retain; or in our terminology, an enacted meta-level learning affordance. Alternatively, if the students expressed strong dissatisfaction alongside what they wished to have learned, we interpreted this as a discursive meta-rule the students wanted to change; or in other words, a missed meta-level learning affordance. While the student-centered analysis mainly pointed toward enacted/missed affordances for meta-level learning, a similar approach was used regarding affordances for object-level learning.

Regarding the analysis process of identifying KMEs, it is important to acknowledge a potential discrepancy between the small number of interviews on each lesson and the idea of a KME as a memorable experience with shared meaning for many students in class. We suggest that the inferences made regarding events with the potential to also be memorable and meaningful to other students could be reasonably supported when considering the following. First, we noticed a phenomenon where already after 1–2 interviews in regard to each of the eight lessons (see Section “Context, participants, and problems of interest”), we were able to anticipate which lesson events would also be mentioned as meaningful in the subsequent interviews – even concerning classroom events we had not originally suspected students to speak of. We were able to do so based on the strong emotions in the students’ descriptions of these events, accompanied by a shared meaning. We suggest that it is also the shared emotional intensity and meaning associated with the identified KMEs (as illustrated in the Findings section) that supports the perceived significance of these events not only for the interviewed students, but also for the other students in each respective class. Secondly, the events that emerged as KMEs in Lesson-P and Lesson-N and their associated learning affordances were validated by additional collected data (Yin, 2011; see also Section “Data collection”), as well as by similar themes expressed by students who participated in our wider research project (which to recall, included 36 stimulated-recall interviews in relation to eight filmed lessons).

Findings

The initial analysis stage (stage (a) in Section “Data analysis”) resulted in a division of each lesson into a list of consecutive events: 20 events for Lesson-P and 24 events for Lesson-N (see Appendices A and B). We note that some events were as short as several seconds, such as events consisting of only one spoken sentence by the instructor. Subsequently, the main analysis process (stages (b) and (c) in Section “Data analysis”) resulted in the identification of two events in Lesson-P and three events in Lesson-N, associated with a shared meaning by the interviewed students. Out of these, one particular event in each lesson was repeatedly addressed by the students in strong affective terms and consequently identified as a key memorable event (KME). Both KMEs occurred in early stages of the solution process, and the student interviews suggest these events shaped the learning experience for the remainder of the solution. The following sections discuss the details of these events, their context in the lesson, the students’ perspective on them, and the associated affordances for learning.

Key memorable events in the lessons

The key memorable event in Lesson-P

In Lesson-P, a particular event, repeatedly addressed by the students and referred to as meaningful, was identified as a KME (event no. 3; see Figure 2 and Appendix A). The identification of the KME was based on student accounts that shared a common theme as to why the event was memorable (as opposed to event no. 2, for example, where no common theme could be found), as well as the affective nature of the event as experienced by the students and expressed throughout the interviews. The KME regarded the instructor’s decision not to begin solving the problem immediately after it had been written on the board, but rather to first guide the students through two mathematical “observations” (as termed by the instructor). These “observations” were initiated by the instructor’s statement:

“Let’s first try to understand what’s going on here. I want us to make some observations.”

Figure 2. Part of the table-of-events of Lesson-P (“x” denoting the event was memorable for Student-P#; Event 3 identified as a KME).

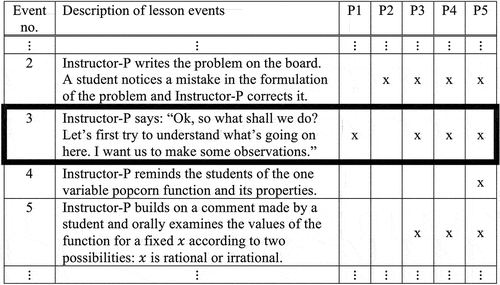
The mathematical content of these “observations” was presented and discussed over approximately 10 minutes (events no. 4–12), and included a step-by-step analysis of how the function behaves, theorems that could potentially be used to solve the problem, and possible student misconceptions and mistakes. However, it was the instructor’s “declaration of intent” to discuss the thought process of how to approach the challenging problem, that was identified as a KME of strong positive nature for the students.

To provide mathematical context for the KME, the first “observation” entailed that for a fixed $x$ we get $\underset{0}{\overset{1}{\int }}f\left(x,y\right)dy=0$ and therefore the iterated integral $\underset{0}{\overset{1}{\int }}\left(\underset{0}{\overset{1}{\int }}f\left(x,y\right)dy\right)dx$ equals zero. After having written the title “Observation no. 2,” Instructor-P asked the students: “What happens if I fix $y$?” The students participated in the discussion regarding a fixed $y\notin \mathbb{Q}$ and a fixed $y\in \mathbb{Q}$, the latter giving the Dirichlet function $D\left(x\right)=\left\{\begin{array}{cc}\frac{1}{q}& x\in \mathbb{Q}\\ 0& x\notin \mathbb{Q}\end{array}\right.$. This led the class to the conclusion that the integral $\underset{0}{\overset{1}{\int }}f\left(x,y\right)dx$ does not exist (according to Riemann’s definition), and therefore it is impossible to calculate the opposite-direction iterated integral $\underset{0}{\overset{1}{\int }}\left(\underset{0}{\overset{1}{\int }}f\left(x,y\right)dx\right)dy$.

The “observations” part of the lesson concluded with two corollaries regarding the function: 1) its double integral exists, yet the iterated integral (in one of the directions) does not; and 2) it demonstrates the importance of the continuity assumption in Fubini’s theorem which enables the calculation of the double integral $\int \underset{D}{\int }f\left(x,y\right)dxdy,D=\left[0,1\left]\times \right[0,1\right]$ as the iterated integral $\underset{0}{\overset{1}{\int }}\left(\underset{0}{\overset{1}{\int }}f\left(x,y\right)dx\right)dy$. It was only then that the instructor admitted that everything discussed so far “does not yet answer our problem.” He subsequently wrote on the board: “So how do we solve [the problem]?,” and then proposed: “In such a case we need to follow the definition.”

The students’ accounts of Lesson-P and its KME

The students’ attitude toward the lesson segment dealing with the problem of interest was identified as positive in the following manner. At different levels of explicitness, all students reported that this lesson and its teaching were good, while unsolicitedly focusing on the “popcorn-function” problem specifically – typically even prior to any explanations from the interviewer. For example, even before being informed what the interview would be about and on which problem it would focus, Student-P1 had begun talking about the “popcorn-function” problem:

“You came to a very special lesson […] The instructor chose a non-standard problem [subsequently clarified as the “popcorn-function” problem by the student] to convey his messages. I really loved it. It really breaks the routine. It feels like the instructor is investing in your learning process rather than acting in a routine way.”

Student-P2 asserted: “You came to a good lesson, really!,” and referred to the discussed problem as “The problem” of the lesson (emphasis in intonation). Student-P3 said: “The lesson was interesting. […] The first function [the problem of interest] was different and new.” Students P1, P3, and P4 called the problem “beautiful.” We note that these evaluations of the lesson and problem are not self-evident, especially when considering the students’ accompanying report of not understanding the solution to the problem (see Section “Learning affordances in Lesson-P”).

Moreover, it is toward the “observations” part of the lesson (events no. 3–12) that the students explicitly provided positive descriptions of what had happened. The students referred to the observations as “extremely important” and “indispensable,” and as Student-P3 stated: “with the two observations he [the instructor] gave me exactly what I wanted.”⁶ Furthermore, the instructor’s statement in event no. 3, declaring the approach toward the problem by first making observations, was identified as a KME based on the interviews of all students except Student-P2 (who during the lesson was sure that the “observations” part was the actual solution, which led her to later confusion). A repetitive statement in the students’ interviews was that through the observations the instructor revealed the thought process of how to approach the problem. This is exemplified below in several excerpts from the student interviews.

Student-P1 stopped the video when the instructor declared his intent of “making observations,” and said:

“I really love it when they [instructors] write a problem and immediately afterwards talk to the class with the following approach: ok, I’m a student now, I got this problem, how do I approach it? […] Where do I begin? Like, let’s start playing with it, let’s see what’s going on here. I really appreciate it when a teacher doesn’t immediately ‘toss’ the solution on the board because it’s clear to him […] but rather puts himself through our eyes when looking at the problem.”

The interviewed students emphasized that the initiation of the observations was essential for their learning, as these helped them understand not only what needed to be done, but also the reasons behind it, as illustrated by the words of Student-P3:

“If he [the instructor] had begun directly from the solution, then it would have been a solution that was dropped on me […] [If this had been the case] I would have understood this was what you should do, but wouldn’t have known why.”

We suggest that the above student statements stand out when considering that the solution itself does not require any direct use of the gained knowledge from the “observations” part of the lesson. Furthermore, we note that as suggested in all student interviews, the students regarded the discourse presented by their instructor in the “observations” part as a discourse that takes their needs into account, as it reveals a mathematical thought process that acknowledges a student perspective.

The key memorable event in Lesson-N

Similarly to Lesson-P, also in the case of Lesson-N the interviewed students consistently referred to a single event that occurred soon after the problem had been presented on the board. After having drawn the graph of the function, written what needs to be proven according to the “epsilon-delta” definition, and described general principles for the solution, Instructor-N told the students the following (event no. 7 out of 24; see Figure 3 and Appendix B):

“In the beginning you may experience some lack of understanding. Once we reach the end, you’ll understand where I took the numbers from, that initially might look a bit weird.”

Figure 3. Part of the table-of-events of Lesson-N (“x” denoting the event was memorable for Student-N#; Events 7 and 8 identified as a combined KME).⁷

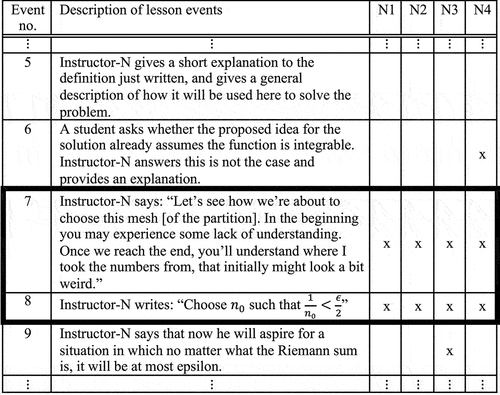
Subsequent to this meta-level statement, the instructor wrote the following on the board (event no. 8):

Choose $n_0$ such that $\frac{1}{n_0}\hspace{0.17em}<\frac{\in }{2}$

The consecutive events no. 7 and 8 were originally considered as two separate events since students referred to them separately. However, we decided to treat these events as a single (combined) KME due to the common theme found in the student interviews, as well as their proximity in time. We suggest that the fact that the students decided to stop the video twice in a row in a short time segment whilst repeatedly expressing similar emotions of strong dissatisfaction, gives further support to our identification of this episode as a KME (see Appendix C for an overview of the solution to the problem, which could provide the reader further mathematical context for the identified KME).

The students’ accounts of Lesson-N and its KME

The students in Lesson-N expressed negative emotions toward the lesson – particularly toward the part of the lesson that dealt with the problem of interest. Similar to Lesson-P, also the students here had unsolicitedly begun discussing the “popcorn-function” problem even before watching the video. Similar conveyed thoughts and feelings toward this problem that repeated in the different interviews included strong statements such as being “totally lost,” “super confused,” and “it was really hard for me to follow.” Student-N1, for example, sighed loudly, referred to the problem as “the most un-understood problem,” and subsequently said:

“I did not enjoy this lesson at all. All the time I felt lost in every possible direction. I came out more frustrated than I came in.”

A similar perspective on the problem given by Student-N4 was:

“I thought the problem was delusional, I didn’t understand what’s going on there.”

The data suggest that the overall student attitude toward the entire lesson was rooted in the identified KME. It was the instructor’s choice of $n_0$ that served as a key event in the lesson where all four interviewed students stopped the video and expressed similar feelings of strong dissatisfaction. The main criticism they conveyed was that the instructor did not explain the logic behind his choice, nor reveal his thought process leading to it. Without these as a support for the learning process, the students felt uncertain of their own abilities to independently solve such a challenging problem.

For example, Student-N1 expressed feelings of strong anger during the identified KME:

“He’s saying a sentence: ‘I’ll give you numbers now, at the end you’ll understand where they’re coming from.’ […] And you say to yourself: I wouldn’t have known how to get to that if you hadn’t shown it to me. […] It really pissed me off. He pulls the answer out of a hat, and I don’t know how he got to it.”

Student-N2 shared similar thoughts in a rather cynical and annoyed tone of voice:

“If I’m being told a fact, then cool. But how will I get to that fact later on? […] As far as I remember, he also didn’t explain it later, how he got to it. I just saw it worked out. Fine.”

Also Student-N3 shared a similar feeling of frustration:

“I remember I kind of got stuck on it. […] Because he decided, and then said ‘we’ll see later’. And every time I’m being told ‘later’, it’s really hard for me. Like, come on, why don’t you say it before for a second? And where did you think of bringing this $\frac{1}{n_0}$ from? And what’s its goal, like, what is its role in the story? So this is how I felt back then. And this is also how it feels to me right now.”

Later in the interview, Student-N3 returned to talk about the choice of $n_0$ and added the following:

“Never in my life would I have come up with this $\frac{1}{n_0}$ and what it means.”

The above students’ statements convey similar thoughts on what was perceived by them as a frustrating learning experience, which was rooted in the single identified KME. The students’ reports reveal they would have wished to be included in a discourse on how to approach and think about the problem. Moreover, the data suggest that the level of emotional intensity in Lesson-N was triggered by a promise for such a discourse to take place, which was ultimately left unfulfilled.

Enacted and/or missed learning affordances associated with the instructors’ discourse

Learning affordances in Lesson-P

As has been made evident in Section “The students’ accounts of Lesson-P and its KME,” the students perceived Lesson-P as special and good, primarily pointing at the problem of interest, and more specifically referring to the instructor’s mathematical discourse initiated in the KME. However, all students additionally reported the problem to be very challenging, and the unexpected impression we got was that the students did not fully understand the solution, nor express confidence in their abilities to solve similar problems independently. For example, Student-P1 admitted that a key line in the solution seemed to him like “gibberish”; Student-P3 found the same line to be full of incomprehensible transitions which she referred to as “jumps”; and Student-P2 referred to the same line with: “What??? Well, he said it, so it’s probably true,” and later in the interview admitted: “If this problem were to be in the exam, I wouldn’t succeed in solving it.” In our theoretical terminology, the students’ self-reported lack of understanding of the solution can be viewed as a missed object-level learning affordance.

Nevertheless, and initially as a surprise to us, the aforementioned students’ statements were not accompanied by any explicit expressions conveying negative emotions. Additionally, such statements barely appeared in other parts of the interviews, and did not even appear at all when the students were explicitly asked what they were displeased with during the lesson. Considering this, it is important to ask whether the students managed to learn something in this lesson, and if so, what could this be? We suggest this could be reasonably answered if we examine whether and how the KME played a supporting role in students’ learning – that is, what affordances for learning did exist according to the students’ perspective.

As evident in the students’ interviews, the learning affordances in Lesson-P related specifically to the identified KME and the subsequent “observations” part. It is interesting to note that even though the discourse in this part of the lesson was not directly utilized in the subsequent discourse on the solution, it was nonetheless perceived as an essential and indispensable part of the lesson (see also Section “The students’ accounts of Lesson-P and its KME”). Indeed, in the interviews the students addressed different enacted learning affordances they associated with this part of the lesson.

In terms of object-level learning affordances (i.e., the expansion of the students’ existing mathematical discourse on Riemann integrability), the students referred to two mathematical conclusions made by their instructor that were new to them:

“Along the way he [the instructor] ties up lots of loose ends that we less knew about, because all these integration theorems have unambiguous conditions that are very easily confusable.” [Student-P4]

In particular, the first conclusion regarded the “popcorn function” as a counterexample to the statement “The existence of a double integral implies the existence of both iterated integrals”; as illustrated by Student-P3:

“He [the instructor] used the observations to show that the “popcorn function” is a counter-example to all sorts of things. That even if in the end we’ll show that it’s integrable and its integral equals zero, then it doesn’t have to be that its iterated integrals exist.”

The second conclusion emphasized the importance of the continuity condition in Fubini’s theorem – that it is not enough to require the function to be integrable; as, for example, shared by Student-P5: “That’s strange! I was sure the condition was for the function to be integrable […] in order to be able to convert the double integral into iterated integrals.” A repeating theme here was that the students seemed to be surprised and puzzled by this conclusion, and wanted to double-check the theorem conditions in the notes they had taken during the preceding lecture (that is, whether the requirement was for an integrable or continuous function). In this regard, we suggest the students’ responses provide an empirical illustration to our focus on enacted rather than lived objects of learning (see Section “Theoretical underpinnings”) – since at the time of the interview (which was soon after the lesson), the students had not yet endorsed the new mathematical narrative (see Sfard, 2008).

The findings above illustrate that while the discourse on the solution was perceived as a missed object-learning affordance, the students were provided with alternative object-level learning affordances earlier in the lesson, which might have served to neutralize potential negative emotions toward not understanding the solution. While this explanation might serve as an initial conjecture to make sense of the students’ positive attitude toward the lesson, we note that the positive emotions the students expressed in regard to the lesson were not pointed toward the object-level learning affordances above, but rather toward what we interpret as meta-level learning affordances stemming from the identified KME. We recall that it was the instructor’s declaration of “Let’s first try to understand what’s going on here, I want us to make some observations,” that was identified as a KME of positive affective nature. Accordingly, based on the students’ statements that the lesson was special and non-routine (see Section “The students’ accounts of Lesson-P and its KME”), while portraying strong positive emotions specifically in regard to the KME of initiating “observations,” we suggest that this KME initiated a change in the meta-rules of the discourse the students were pleased with; or in other words, that the act of solving the problem was now done in a different way that provided new learning affordances to the students.

According to the students’ interviews, the act of solving the problem by the instructor incorporated a student perspective in his discourse. To recall (see Section “The students’ accounts of Lesson-P and its KME”), Student-P1 said that Instructor-P talked to the class with the approach of “I’m a student now” while “put[ting] himself through our eyes when looking at the problem.” Another illustration comes from Student-P4, who described the way in which the instructor led the discourse as incorporating a student perspective:

“Only now I see how structured he is. When you’re in the lesson, you think he didn’t plan what he did. […] And it’s good, because it really allows you to think along with the problem. […] When he did it in the lesson I understood: Wow, [name of Instructor-P], you’re a genius! You did it really elegantly! […] He tries to give you the feeling that he’s solving it with you. He says: ‘Let’s think, people, I really don’t know how to do it. […] Now we’re thinking.’ And then you believe he’s not fooling you, so you start thinking yourself, because you don’t tell yourself: ‘He already thought about it, so he should just tell me [the solution] already’.”

The above quote suggests that the instructor’s discourse allowed the students to think along with him, by having the instructor look at the problem as a student himself who is trying to solve it for the first time. Another aspect of a student perspective that existed in the instructor’s discourse was given by Student-P2, who shared that the instructor’s acts in the “observations” part of the lesson were most likely what she would have done had she attempted to solve the problem independently: “Probably, it’s a mistake students had done in the past. Probably it’s what I would have done: calculate an [iterated] integral, freeze $x$, […], and then say: ‘Ok, cool, it’s zero’.”

In addition to the students’ explanations to their interpretation of a student-perspective in their instructor’s discourse, we identified instructor utterances such as “hmm” and “very weird” regarding mathematical conclusions that were unlikely “weird” for the instructor; these were noticed by us not only while re-watching the lesson, but also in the observation-notes taken during the lesson itself. Further supporting evidence was found in the post-communication with the instructor, who shared that he chose to include this problem in the lesson based on mathematical struggles he had experienced with the “popcorn function” as an undergraduate student himself.

Nonetheless, the interviewed students additionally acknowledged a complementary dimension in the instructor’s discourse, which was not only about incorporating a student approach, but also revealing the thought processes and problem-solving heuristics of an expert problem-solver. To recall (see Section “The students’ accounts of Lesson-P and its KME”), Student-P3 claimed that the “observations” part revealed the why behind the instructor’s approach for the solution. Similar ideas were also conveyed by the other students, as, for example, illustrated in the following excerpt from Student-P5’s interview:

“It’s the whole thinking process. Without the observations, we wouldn’t have been able to move forward. They’re things you need to pay attention to: examine the known information, try to understand what you’re being asked, analyze, construct.”

One such heuristic in the instructor’s thinking process regarded a systematic use of fixing one variable at a time in order to visualize a graph of a two-variable function; as for example, stated by Student-P3: “This was the moment I started to understand the function. As soon as he told me to do this observation, […], that you just divide it into rows and columns,⁸ I understood what’s happening with the function […] and could visualize it.” Another heuristic was to try solving the problem in a new way in case an initial attempt for a solution fails; as shared by Student-P2: “And then he said: ‘Oops, we’re stuck’. This tells you that if you try one method, there’s another one to try. If you get stuck, it’s ok, you should go back to basics and use the definition, or try other theorems” (we note that according to Marmur & Koichu, 2016, this discursive rule is not a norm in the undergraduate classroom). Furthermore, the instructor’s discourse revealed a problem-solving heuristic of “mathematical play” (Featherstone, 2000), which, as explained by Sinclair (2004), is a strategy mathematicians use to frame an area of exploration. According to Student-P1, this was the strategy used by the instructor with the initiation of the “observations”:

“You get a scary problem like this one. […] First thing you say: ok, what can it be? I’ll start playing with it. Just let your imagination fly regarding what you can do with it. Not even with an approach of how do I solve it, but how do I play with it. Where can I bring this to, regardless of the solution? So this is what [name of Instructor-P] did here at the beginning.”

Learning affordances in Lesson-N

Overall, the students of Lesson-N found the solution presented by the instructor to be incomprehensible, while using expressions such as “the most un-understood problem,” “the whole problem was unclear,” and “I was totally lost.” Additionally, during the interviews they expressed negative emotions toward the lesson, while heavily criticizing the instructor’s discourse in class. This is particularly intriguing in light of the fact that, from our perspective, Instructor-N made reasonable and decent efforts in explaining the solution. When examining our constructed list of the lesson events (see Appendix B), we found that the instructor presented the solution in a logical order without any mistakes (indicating being prepared for class); answered student questions when they arose (events no. 6,15,18); at different occasions had explained in advance the mathematical ideas that were about to be used (events no. 3,5,11,15,20,23); and at different times explained mathematical claims that had just been made (events no. 5,11,13,16,18,22). Therefore, when considering the students’ opinion of the lesson, we may ask ourselves how and why all this “went wrong” when considered from a student perspective. This question is of particular relevance when recalling that also the students of Lesson-P described the solution in terms such as “gibberish” and “full of jumps,” though ultimately chose to put forward an opposite experience.

In addition to statements presented earlier on the difficulties experienced by the students of Lesson-N (see Section “The students’ accounts of Lesson-N and its KME”), Student-N3 and Student-N4 shared their recalled puzzlement of not understanding why it made sense for the integral to equal zero to begin with (prior to a formal proof). Another mathematical difficulty was expressed by student-N1, who claimed she did not understand why the Dirichlet function was not integrable, yet the popcorn function was. Student-N1 additionally attempted to independently deal with the problem and its solution after the lesson, yet ultimately claimed:

“Till today I don’t know how to reach it [the solution]. […] He [Instructor-N] makes steps that in the end will be combined to a big picture, but he doesn’t explain to us why he wants you to do these steps, and what they will contribute in the end.”

Consequently, as it is difficult to speak of what the students might have learned according to their interviews, we may speak instead of what they shared they wished to have learned. This addresses a student perspective on the affordance for learning – that is, what the students themselves thought and believed was possible to be learned in class.

When describing their recalled thoughts and feelings experienced during the KME, the students stated they would have liked to be shared with the thought process of how to reach the solution to the problem. For example, as expressed by Student-N1:

“It’s just that it really bothers me that he presents the solution by the order of the proof and not by the order of how you think about the proof. […] Like wait a minute, where did you get them [the numbers] from? In the end it all works out. But it doesn’t help me with how to solve a problem.”

Student-N2 raised her voice and stated assertively:

“He should explain why it has to be that $\frac{1}{n_0}\hspace{0.17em}<\frac{\in }{2}$, like, where does it come from?! As far as I remember, he didn’t do that. It just ‘worked out’.”

In this regard, the students repeatedly referred to the unfulfilled promise made by the instructor to later in the lesson explain where the “weird numbers” came from; as illustrated in the following excerpt taken from the interview of Student-N4 (also see other excerpts in Section “The students’ accounts of Lesson-N and its KME”):

“He [the instructor] said: ‘let’s choose $n_0$ such that $\frac{1}{n_0}\hspace{0.17em}<\frac{\in }{2}$’. So he said: ‘you’ll see, now you don’t understand why, but it will work out’. So I said ok, let’s move on, but, hmm … But it didn’t work out for me.”

Furthermore, in the case of Lesson-N there were two other events the students referred to (events no. 3 and 11), which “echoed” the same ideas the students expressed about the KME. While the KME surrounding the choice of $n_0$ was referred to by students most strongly and emotionally, having two additional classroom events students conveyed similar thoughts about, gives further support for the validity of the suggested findings. For example, as shared by Student-N1 regarding event no. 11:

“You see that he first writes […] what you do, and then explains. But really, how was I supposed to come up with it if he didn’t show me how he came up with it? Like, he told me this is how it’s done, [and] explained why. But this is specific to this problem. It won’t be [relevant/applicable] now for any other problem.”

The above statements indicate that the students in Lesson-N wanted the mathematical discourse in class to address and reveal the instructor’s thought process on the one hand, whilst taking into account a student perspective on the other hand. In other words, we suggest that the students wished for the learning affordances to originate from a meta-level discourse that reveals the instructor’s approach in a way that the students would be able to generalize the underlying ideas for future problems.

Discussion

In line with current approaches in mathematics education research, in this paper we have focused on the communicational setting of the undergraduate mathematics classroom, and examined affordances for learning in a Real-Analysis lesson in the context of the teaching that took place. In particular, to address the teaching-learning interaction, we have used a discursive lens for the teaching and an affective lens for the learning, considering the recognized interrelationship between discourse and emotion (e.g., Evans et al., 2006; Heyd-Metzuyanim & Sfard, 2012). In the following discussion, we first provide a summary of the findings leading to our suggested notion of heuristic-didactic discourse; and subsequently highlight theoretical and practical contributions regarding discursive and affective perspectives on the teaching and learning of undergraduate mathematics.

Summary of findings

In this paper we have presented a case of two lessons in the same course. Both lessons were taught by experienced and reputable instructors; both lessons dealt with challenging, mathematically-related problems; in both lessons we identified reasonable efforts made by the instructors to explain the solution; and in both lessons the students reported a significant lack of understanding of the presented solution. However, even though the students in both lessons reported feelings of “being lost” during the solution presentation, the accounts they chose to share of how they experienced the overall learning process in class were opposite in nature. Taking an affective perspective, we utilized the construct of Key Memorable Events (KMEs; Marmur, 2019) to identify classroom events that could elucidate the difference in the students’ reactions. The KMEs that seemed to have shaped the students’ learning experience in each lesson were characterized by the kind of discourse led by the instructor.

In particular, we suggest that the students’ emotionally-loaded responses to the KMEs point toward a change in the meta-rules of the discourse that the students wished to either retain, in the case of Lesson-P, or to have changed, in the case of Lesson-N. While the meta-rules of instructors’ discourse are not typically made explicit to students (Pinto, 2019), the data show that for the participating students in these two lessons, the discursive acts of the instructors became objectified, thus creating a meta-level discourse about the object-level discourse of solving the problem (see Cobb et al., 1997; Rogalski, 2000; Sfard, 2008). In the case of Lesson-P, the positive emotional reactions further suggest that the meta-level discourse led by Instructor-P succeeded in balancing both expert and student perspectives, an act which we interpret as attending to students’ both cognitive and affective needs. We call a meta-level discourse that presents heuristics monitored from an expert’s point of view, yet derived from a student’s point of view – heuristic-didactic discourse.

The value undergraduate students attribute to this kind of discourse as indicated by this study is emphasized when contrasting the findings from Lesson-P to those of Lesson-N. In Lesson-P, the single identified KME regarded a heuristic-didactic discourse the students were pleased with, and the data suggest this event shaped the students’ positive attitude toward the lesson. In the case of Lesson-N, however, the single KME pointed toward a heuristic-didactic discourse the students wished took place, yet was missing, and it seems this KME shaped the students’ overall negative attitude. Sfard (2008) regards meta-rules of discourse as rules that “speak about the actions of the discursants, not about the behavior of mathematical objects” (p. 201). As is evident by the data presented earlier, all interviewed students of Lesson-N were missing the meta-level regarding why Instructor-N was acting mathematically the way he did. Additionally, whereas the students of Lesson-P recognized a student perspective in their instructor’s discourse, the students’ statements on Lesson-N revealed that they did not feel the discourse on the problem addressed how they would approach it themselves.

It is important to note that the difference in the students’ learning experiences in the two lessons may also stem from alternative explanations. It might be that the students of Lesson-P generally possessed a more positive attitude toward mathematics and/or the course compared to the students of Lesson-N, and this might have shaped real-time emotional states experienced during the lessons. However, observing the data, we could not find evidence of a connection between the students’ attitude toward the subject and how they felt during the lesson. As an example to the contrary, Student-N1, who felt frustrated during the solution in class and admitted she “did not enjoy this lesson at all,” shared the following: “I have always loved mathematics. […] I wanted to study mathematics [as a major] […] Last semester Real Analysis was my favorite subject.”

Another possibility is that the students’ experiences in the lessons were influenced by when in the semester the lesson took place. It could be reasonable to conjecture that the students in Lesson-P were more familiar with the general concepts and ideas of the course, as well as more used to their instructor’s style of teaching, as it occurred later during the semester. However, it could be equally reasonable to expect Lesson-P to be accompanied by students’ affective responses to the contrary, as the concepts of two-variable functions and their associated double integrals have been shown to be more complex and challenging for students compared to their one-variable counterparts (e.g., Martínez-Planell & Gaisman, 2012; McGee & Martínez-Planell, 2014).⁹ While learning and affect are complex phenomena often shaped not by a single factor but a multitude of situational circumstances, we argue that any alternative interpretations of the context should first and foremost not contradict the student perspective central to this study. In other words, it would be presumptuous to negate the students’ experience of Lesson-P when they explicitly claim that they experienced positive emotions because of the instructor’s discourse. Accordingly, our intention is not to claim that the instructors’ discourse was the sole contributing factor shaping the students’ experience, but rather acknowledge the significance of this discourse as emerging from the student-centered data – and more generally, the value such a student-centered perspective may offer to mathematics education research. We highlight that the students in our study did not raise any of the alternative explanations hypothesized above; rather, both in Lesson-P and Lesson-N, they linked their experienced affective states during the lesson to the type of discourse led by their instructor as shown in the findings – a phenomenon we conceptualize as “heuristic-didactic discourse.” In what follows, we elaborate on the meaning we attribute to this concept according to our two theoretical lenses: discourse and affect.

On undergraduate mathematics teaching and instructors’ heuristic-didactic discourse

The focus on the instructor as the leader of discourse sheds light on a built-in tension in the teaching of problem solving in the lecture-based classroom. On the one hand, high-quality instruction should be sensitive to students’ cognitive and affective needs, and take into account the students’ own ways of thinking when approaching a challenging problem (e.g., Jaworski, 2002; Simon, 1995). On the other hand, the undergraduate instructor needs to support a shift in students’ mathematical thinking from secondary-school mathematical thinking with a strong intuitive basis, to a more advanced mathematical thinking based on formal definitions and logical deductions (Tall, 1992). From a discursive perspective, this transition involves a change toward a new mathematical discourse incommensurable with the former one, gradually occurring through the exposure of students to the instructor’s discourse (Sfard, 2014).

To recall, we defined heuristic-didactic discourse earlier as a meta-level discourse that presents heuristics monitored from an expert’s point of view, yet derived from a student’s point of view. The first part of this definition, which focuses on a discourse that reveals an expert’s perspective, resonates with previous mathematics education research. For example, Mason (2002) suggested undergraduate instructors should expose their “inner monologues” when teaching. This would enable students to learn from their instructors’ inner thoughts, see how masters of the discipline approach mathematical problems, and even realize that also mathematicians make mistakes. Other studies (e.g., Fukawa-Connelly, 2012; Viirman, 2015) identified that instructor discourse involving rhetorical questions could be used to model mathematical thinking by an expert in the field. As explained by Fukawa-Connelly (2012), these questions “can be understood as the internal dialog that a mathematician might engage in when approaching a proving task” (p. 342). And as also discussed earlier in the paper, Sfard (2014) argued that a student’s exposure to the instructor’s discourse, while attempting to comprehend how the expert would approach various situations, is a fundamental condition for undergraduate learning.

However, when examining the education literature, we note that the balancing of expert and student perspectives in undergraduate teaching – which is at the basis of our suggested notion of heuristic-didactic discourse – has been proven to be pedagogically challenging and therefore requires further research. For example, Fukawa-Connelly (2012) reported on an instructor with pedagogical expertise who placed emphasis on developing her students’ proof-writing abilities. The instructor’s discourse incorporated many rhetorical questions that modeled her mathematical thinking, as well as promoted significant student participation, which on the surface may seem student-centered. Nonetheless, the student engagement regarded only trivial facts, whereas the instructor answered all difficult questions herself – thus developing only limited student responsibility for learning. In another study, Kontorovich et al. (2019) illustrated that even when a student perspective is taken in the discourse, this is not always conducive to students’ learning, since students’ discourses do not necessarily map systematically onto a parallel expert discourse. Consequently, “[e]ven with pedagogical intervention, students can juggle discourses at their reach to substantiate the [mathematical] narratives that they created” (p. 73).

The current study indicates that students recognize affordances for meta-level learning when the instructor not only verbalizes her own inner thoughts, but also serves as the voice of the students’ inner discourse, which under the norms of the lecture-based classroom remains silent. According to Sfard (2008), meta-level learning (i.e., a change in the meta-level rules of the discourse) is dependent on students’ experience of a commognitive conflict – which occurs when “different discursants are acting according to different metarules” (p. 256). In the undergraduate classroom, such a conflict may arise as a result of the incommensurable discourses of the instructor and students. Based on our findings, it seems students would like their instructors to hold two (possibly) incommensurable discourses simultaneously. Utilizing Sfard’s terms, we suggest that a heuristic-didactic discourse, which incorporates both expert and student perspectives, might require the instructor to enact, and thus expose, the commognitive conflict students are ultimately expected to experience themselves.

We acknowledge that our theoretically-driven conceptualization of instructors’ heuristic-didactic discourse as balancing two potentially incommensurable discourses simultaneously would require further empirical investigation and operationalization in future studies. However, we additionally note that even with such research endeavors, the results of mathematics education studies stemming from a discursive perspective are often not easily translatable into specific implications for teaching. It seems that the products of such studies – an account of nuanced discursive patterns in development – are generally complex and context-dependent, and accordingly may not be immediately appealing to mathematics teachers and instructors who are in search of explicit overarching guidelines for teaching (Koichu, 2019).

Accordingly, we suggest that the additional theoretical lens we have used here, which stems from an affective-cognitive representational perspective (e.g., Goldin, 2000; Marmur, 2019), may offer an entry point for bridging the discussion between subtle discursive patterns and teaching guidelines, by considering the surrounding pre-conditions for heuristic-didactic discourse to take place. While we can imagine undergraduate mathematics instructors to be able to represent an expert perspective when teaching, how might they be able to incorporate a student/novice perspective in their discourse? We propose this might require instructors to engage in a continual process of reflection, while drawing on their past experience as students themselves (e.g., to recall, Instructor-P chose the problem based on struggles he had experienced with the “popcorn function” as an undergraduate student himself); prior teaching experience (e.g., recalling students’ questions and struggles from previous years); knowledge of their current students in both the cognitive and affective domains (e.g., which problem-solving heuristics are their students familiar with, but also how may the students’ attitude toward mathematics support or hinder their engagement with certain problem-solving heuristics?); and lastly, plausible pre-conjecturing of how their students might engage with a specific mathematical problem during the lesson planning stage. Nonetheless, we note that such efforts in search of a novice perspective might not be sufficient on their own, as the instructor’s actual discourse would still need to resonate with the students themselves – requiring a subsequent inquiry into and verification of the students’ perception of the actual discursive events (which, as illustrated in this study and further discussed in the following section, is not always self-evident).

On undergraduate mathematics learning and students’ emotions in the classroom

Considering an affective perspective on learning, it is widely acknowledged that students report satisfaction when they are able to make sense of the mathematics they are learning, and that understanding in turn serves as one of the greatest motivators for learning (e.g., Hannula, 2006; Schukajlow et al., 2017). However, the case of Lesson-P illustrates that a lack of understanding can nevertheless be accompanied by positive student emotions. We argue this phenomenon is not self-evident, and propose an explanation based on what we have identified as heuristic-didactic discourse.

We suggest that the students in Lesson-P were not only appreciative of the heuristic-didactic discourse and the learning affordances it provided, but that this discourse may have also had a neutralizing effect on the potential negative emotions related to not understanding the solution. Appraisal theories of emotions propose that emotions are triggered by an evaluation (appraisal) of an event in regard to its significance to one’s motivations and goals (e.g., Moors et al., 2013). This implies that students’ regulation process of motivations and goals is capable of shaping or altering the emotional states they experience (Hannula, 2006). In these terms, it could be argued that the KME of heuristic-didactic discourse played a role in the students’ goal regulation during the lesson and consequently in their emotional evaluation of the lesson. This by managing to create a shift from an initial normative goal of “I want to understand the solution” (or “I want to be able to solve such a problem in the exam”; see also Marmur & Koichu, 2016), to a new goal of “I wish to understand how to approach such problems even more than I wish to understand how to solve this one” – a need that was addressed through the instructor’s heuristic-didactic discourse.

Furthermore, the findings herein provide further empirical evidence for the theoretical notion of a KME (Marmur, 2019), that is, how a single emotionally-loaded state during students’ affective pathways (Goldin, 2000) may have a strong impact on their subsequent learning process and longer-term affect. For example, Weber (2008) demonstrated how one strongly positive experience of success had had a considerable effect on a student’s overall success in a Real Analysis course, by altering the student’s attitude and type of engagement with the material for the continuation of the course. In another study, Liljedahl (2005) suggested that a single “Aha!” moment, experienced by undergraduate mathematics students during a problem-solving activity, substantially impacted their attitudes and beliefs toward the subject. Such findings are also supported in the neuroscientific domain, where it has been shown that brain activity in the amygdala during an “Aha!” experience is associated with solutions that will remain in long-term memory (Ludmer et al., 2011).

In our study, the findings pointed toward a KME in each lesson, as a memorable experience with shared meaning of affective and cognitive nature. We suggest a distinction whether the strong emotions associated with the KME were actually experienced during the lesson or intensified afterward, is of low importance – as ultimately what the students recalled and remembered indicates the significance they attributed to the event, which they carry with them into their future. As noted by Ellsworth and Scherer (2003), “Usually, people’s emotions arise from their perceptions of their circumstances – immediate, imagined, or remembered” (p. 572). In this regard, we find it rather remarkable that out of two 2-hour lessons, the participating students unsolicitedly and repeatedly referred to a single event in each lesson surrounding a common theme. As such, and considering the positive nature attributed to the KME in Lesson-P, we suggest it is likely the students in this lesson would be emotionally “open” to continue their learning process independently at home, and in particular to reexamine and try to understand the uncomprehended solution (see also Example 1 in Marmur, 2019, for similar student behavior).

In the mathematics education literature, it has been recognized that emotions are integral to the learning process, and that the inseparable connection between cognition and affect mediates the interactions between teachers and students (e.g., Roth & Radford, 2011). As Radford (2015) remarks: “Emotions and thinking are not separate entities. They are fused together. We cannot think without emotions.” (p. 45). In relation to our study, we suggest the identified student need for heuristic-didactic discourse is of both cognitive and affective nature, providing us with insight into the ways in which students’ thoughts and emotions are “fused together” when learning mathematics in the undergraduate classroom.

In particular, and as suggested by this study, the undergraduate-student need for heuristic-didactic discourse implies a student preference toward learning via problem solving (Schroeder & Lester, 1989), which is concentrated on thought-processes and knowledge that could be generalized for future problems; this rather than merely the typical learning for problem solving (Schroeder & Lester, 1989), which is focused on a solution-oriented end-result. Moreover, the findings demonstrate that learning-via-problem-solving may even occur in circumstances where learning-for-problem-solving is not achieved. We do not wish to imply that instructional efforts should consequently be directed solely or mainly toward those aspects generalizable to other problems, rather than the comprehension of the solution. However, we do suggest that especially in cases that involve exceedingly challenging solutions that might not be understood in real-time (such as in our reported lessons), it would be advisable for instructors to focus their students’ attention toward the meta-level dimension of the mathematical discourse on the problem. If done carefully, while attending to students’ self-regulation of emotions and meta-affect (see Goldin, 2014), such problems could promote meta-level learning, as well as legitimate struggles and even failures as an integral part of what mathematical problem-solving entails.

Contribution and concluding remarks

In conclusion, this paper offers several contributions to research and practice that are situated at the intersection of affective and discursive perspectives in mathematics education research. From an affective perspective, we note that studies on students’ emotions that are situated in a social classroom setting are relatively rare, particularly at the undergraduate mathematics level (Marmur, 2019; Martínez-Sierra & García-González, 2016); and especially when the learning of advanced mathematics during lectures is in focus, undergraduate mathematics research tends to utilize a purely cognitive perspective (e.g., Lew et al., 2016; Weinberg et al., 2014). Considering this, the study presented herein provides a step toward a better understanding of the interplay between cognition and emotion during students’ learning processes in the advanced-mathematics lecture-based classroom. Moreover, our analysis of the findings provides further support for the utility of the notion of Key Memorable Events (KMEs; Marmur, 2019) – both as a theoretical construct that intertwines cognition and affect (an objective widely pursued by affect researchers), as well as a methodological tool to investigate the interrelation between undergraduate teaching and learning. In particular, KMEs can be used to indicate affordances for a discourse change, which in turn indicates affordances for learning.

From a discursive perspective, the paper provides a contribution to theory by putting forward a new construct termed heuristic-didactic discourse, as a meta-level discourse that integrates expert and novice discourses. While certain aspects of such a discourse have been acknowledged in prior research (e.g., Mason, 2002; Viirman, 2015), we have situated this discourse in a unified manner as addressing students’ both cognitive and affective needs. Furthermore, we believe that the contextualization of the construct of heuristic-didactic discourse in relation to Sfard’s (2008) commognition theory provides a promising avenue for future theoretical and empirical research. In particular, while this study examined the instructors’ discourse indirectly through the students’ perspective, future studies would need to directly analyze the discourse and examine in finer detail how instructors may succeed in conducting two incommensurable discourses simultaneously.

Lastly, the presented study offers practical implications for the improvement of undergraduate mathematics teaching, which could additionally be of relevance to other levels of mathematics education. The student need for heuristic-didactic discourse as indicated by the findings, suggests a shift in the typical undergraduate lecture-based discourse, alongside more emphasis on teaching-via-problem-solving (Schroeder & Lester, 1989) that focuses on generalizable thought processes. As possible longer-term learning-opportunities afforded by heuristic-didactic discourse, we note that according to Sfard (2008), learning is regarded as a lasting change in discourse; and that a change in the meta-rules of the discourse (i.e., meta-level learning) is not likely to be initiated by students on their own. Accordingly, heuristic-didactic discourse in the undergraduate mathematics classroom may serve as an initial point of aid for students to continue a meta-level learning process at home. This implies that undergraduate instructors should put didactic effort in aiding students with how to come up with solutions and proofs, and, as suggested by Güçler (2016), additionally make this an explicit topic of reflection in support of student learning. The findings herein demonstrate this learning opportunity may also be implemented in the common lecture-based classroom, and could provide valuable tools for the learning process the students are required to continue independently outside of class.

We believe that the case-study methodology used in this study, enabled a focused, in-depth inquiry into the complex interrelationship between affect, discourse, and learning, while facilitating conceptual and theoretical development through a process of analytic generalization (Hodkinson & Hodkinson, 2001; Schwandt, 2007; Yin, 2003). In particular, we have attempted to justify our conclusions and their generalizability by focusing on emotionally-loaded events reported to be significant to students’ learning, and contextualizing these within the theoretical approaches in use. Additionally, we note that when returning to our wider corpus of data after having analyzed Lesson-P and Lesson-N (see Method section), we identified the need for and appreciation of heuristic-didactic discourse as a repetitive theme in other student interviews as well, thus strengthening the validity of our findings. Nonetheless, we recognize the need for additional research in order to both further conceptualize the notion of heuristic-didactic discourse, as well as to characterize its potential affordances for student learning in both cognitive and affective terms.

Acknowledgments

We wish to convey our great appreciation for both instructors, who invited us to lessons involving problems they suspected would be highly challenging for students, whilst still being in the middle of a process of searching how to better teach the problems. We are also extremely grateful to the anonymous reviewers and Ronald Boersen for their constructive critiques and insightful suggestions that helped us improve our paper.

Additional information

Notes on contributors

Ofer Marmur

Ofer Marmur is a lecturer/assistant professor of mathematics education in the Department of Mathematics at the University of Auckland, New Zealand. His research focuses on the interrelationship between the cognitive, affective, and social dimensions of student learning, specifically in the context of undergraduate mathematics and teacher education. He was a postdoctoral research fellow in the Faculty of Education at Simon Fraser University, Canada, after having completed his doctoral studies in the Faculty of Education in Science and Technology at the Technion – Israel Institute of Technology.

Boris Koichu

Boris Koichu was a school teacher for eight years prior to switching to an academic career. He is currently a faculty at the Department of Science Teaching of the Weizmann Institute of Science in Israel. His research is in the area of teaching and learning mathematics through problem solving and problem posing, from middle school to university.

Notes

1. The labels “Lesson-P” and “Lesson-N” are here used for ease of reading in comparison to non-descriptive titles such as “Lesson-1” and “Lesson-2”, and should be treated as only indicative of the lesson experience as reported by the participating students. A detailed account of the students’ affective descriptions of the lessons is presented in the Findings section.

2. We note that while the case of the two lessons was briefly presented in Marmur (2019), it was used there merely as a short illustration for the theoretical construct of KMEs suggested in that paper. In the current paper, however, our focus lies in the detailed, full analysis of the lessons, aiming to provide a contribution that is situated at the intersection of affective and discursive perspectives in mathematics education research.

3. We note that Marmur (2019) distinguishes between a theoretical and operational interpretation of the term “many students”, and suggests that upon explicit methodological justification, inferences from a small group of students may be generalized to a whole classroom. For further detail regarding the current study, see Section “Method”.

4. In this paper we refer to this function as the “popcorn function” since this was the name that was predominantly used by the instructors and students in the discussed lessons.

5. Figures 1 and 4 are adapted from “Wikipedia, the free encyclopedia,” by Smithers888, 2008 (https://en.wikipedia.org/wiki/File:Thomae%20function%20(0,1).svg). In the public domain.

6. We note that similar to the other students, also Student-P3 later admitted she did not understand the solution to the problem.

7. Some of the event descriptions have been shortened in Figure 3; see Appendix B for a full account.

8. We interpret “rows and columns” as the student’s way of explaining the idea of fixing one variable at a time in the $xy$ plane.

9. In fact, we heard both opposing conjectures from different researchers in our field during oral presentations of the data.

Appendix A.

List of events in Lesson-P

1. Instructor-P asks: “What is the first problem we solved when we discussed the Riemann integral?” After a student answered this was the “popcorn function” Instructor-P asks: “Does everybody remember it?” Noticing student responses, he asks: “What? Are you bummed out by it?” A student answers: “We’re traumatized.” Instructor-P says: “We’ll go back to it today. Don’t get scared.”

2. Instructor-P writes the problem on the board. A student notices a mistake in the formulation of the problem and Instructor-P corrects it.

3. Instructor-P says: “Ok, so what shall we do? Let’s first try to understand what’s going on here. I want us to make some observations.”

4. Instructor-P reminds the students of the one variable Popcorn function and its properties.

5. Instructor-P builds on a comment made by a student and orally examines the values of the function for a fixed $x$ according to two possibilities: $x$ is rational or irrational.

6. Instructor-P writes the title “Observation” on the board. Then he continues with oral and written explanations that end with the conclusion that regardless of whether $x$ is rational or irrational we get: ${\int }_0^{1}f\left(x,y\right)dy=0$

7. Instructor-P reaches the following conclusion which he writes on the board: ${\int }_0^1\left({\int }_0^{1}f\left(x,y\right)dy\right)dx=0$. He then explains it again to the request of a student, and concludes this only regards the calculation of the iterated integral and does not yet mean that the function is Riemann-integrable in two variables.

8. A student asks whether this calculation would serve as a proper explanation for the value of the integral being 0 according to Fubini’s theorem, if they were to prove the function is indeed Riemann integrable. Instructor-P gives a negative answer since the function is not continuous, which is a necessary condition in the theorem.

9. Instructor-P writes “Observation no. 2” and then examines the value of the function for a fixed $y$ according to two cases: $y$ is irrational or rational. In the case of a rational $y$, Instructor-P asks the students what they think, and student participation continues for a while.

10. A student answered that for a fixed $y\in \mathbb{Q}$, what is obtained is “sort of a Dirichlet function”. Instructor-P explains this to the class and then reminds them of the Dirichlet function and that it is not Riemann integrable in one variable.

11. Some students speak between themselves. Instructor-P overhears this and asks the students: “Did someone here say Lebesgues?” A student admits it was him and says that Instructor-P mentioned the existence of something called “Lebesgues integrable” in the past.

12. Instructor-P explains the conclusion that the iterated integral ${\int }_0^1\left({\int }_0^{1}f\left(x,y\right)dx\right)dy$ does not exist, and then also writes it down.

13. Instructor-P says: “This does not yet answer our problem. It means we have a serious problem.”

14. Students ask questions regarding the relation to Fubini’s theorem. For example: “Isn’t there a version of Fubini’s theorem that requires the function to be only integrable and not continuous?” Instructor-P answers that the current Popcorn function is a counterexample for that.

15. A student asks if Riemann’s function was indeed invented by Riemann. Instructor-P answers he is actually not sure if this is true, and then gives a short description of Riemann’s mathematical activity.

16. Instructor-P writes: “So how do we solve [the problem]?” He then says: “In such a case we need to follow the definition.”

17. Instructor-P explains that they will use what they know from the one-variable Riemann function, and that it is going to be much simpler here.

18. Instructor-P starts the real solution by taking an arbitrary partition $P$ of $\left[0,1\left]\times \right[0,1\right]$ and subsequently an induced partition $Q_P$ of $P$ on the y-axis.

19. Instructor-P evaluates $M_{ij}=\underset{\genfrac{}{}{0ex}{}{x_{i-1}\le x\le x_i}{y_{j-1}\le y\le y_j}}{sup}f\left(x,y\right)$ and explains the supremum is obtained at any rational $x_0$ in the segment, meaning: $M_{ij}=\underset{y_{j-1}\le y\le y_j}{sup}f\left(x_0,y\right)$

20. A student asks a series of questions regarding the explanations just given, yet does not always wait until Instructor-P finishes his answer before asking additional questions.

Appendix B.

List of events in Lesson-N

1. Instructor-N explains that, like all proofs to these kinds of problems, we need to take an arbitrary epsilon in order to show that the sum is as small as we would like it to be, meaning smaller than epsilon.

2. Instructor-N writes on the board: “Let $\in \hspace{0.17em}>0$”.

3. Instructor-N explains that in any problem of this kind, where there is an infinite or finite number of points in which the value of the function is rather big, the principle for the solution is to play with the partition – take narrow rectangles around those points that provide a small contribution to the Riemann sum.

4. Instructor-N writes what needs to be proven according to the definition of a Riemann integrable function (involving Riemann sums).

5. Instructor-N gives a short explanation to the definition just written and provides a general description of how it will be used here to solve the problem (there is an infinite set of points greater than zero, however only a finite set of “problematic” points that will contribute large values; around these “problematic” points it is possible to choose a partition with “narrow segments”, and the rest will contribute 0 or small values).

6. A student asks whether the proposed idea for the solution already assumes the function is integrable. Instructor-N answers this is not the case and provides an explanation.

7. Instructor-N says: “Let’s see how we are about to choose this mesh [of the partition]. In the beginning you may experience some lack of understanding. Once we reach the end, you’ll understand where I took the numbers from, that initially might look a bit weird.”

8. Instructor-N writes: “Choose $n_0$ such that $\frac{1}{n_0}<\frac{\in }{2}$”.

9. Instructor-N says that now he will aspire for a situation in which no matter what the Riemann sum is, it will be at most epsilon. He then says that now we will understand what the relation between $n_0$ and our partitions is, as a result of which we would be able to find a suitable mesh for the partition.

10. Instructor-N writes a claim asserting that in the interval [0,1] there is a finite set of rational numbers $\frac{p_1}{q_1},\frac{p_2}{q_2},\dots ,\frac{p_N}{q_N}$ whose denominator is smaller than $n_0$.

11. Instructor-N explains why the last claim is true and why it is needed for the solution (these are the “bad points” which give large values to the function).

12. Instructor-N writes: “Except for these N ‘bad’ points, for every $c\in \left[0,1\right]$: $0\le f\left(c\right)\le \frac{1}{n_0}<\frac{\in }{2}$”.

13. Instructor-N explains why the last claim is true.

14. Instructor-N writes: “Let us look at an arbitrary Riemann sum” (and also writes the sum explicitly on the board).

15. Instructor-N explains that in any such Riemann sum we have at most N points whose function value is greater than $\frac{\in }{2}$, and in the rest of the points the function value is smaller than $\frac{\in }{2}$. Therefore, we will split the Riemann sum into two sums: one containing the “problematic” points, and one with all other points. Subsequently, a student asks for clarification and Instructor-N provides an additional explanation.

16. Instructor-N writes that there are at most N points such that $0\le f\left(c\right)<M$ where $M=max\left\{f\left(\frac{p_1}{q_1}\right),f\left(\frac{p_2}{q_2}\right),\dots ,f\left(\frac{p_N}{q_N}\right)\right\}=max\left\{\frac{1}{q_1},\frac{1}{q_2},\dots ,\frac{1}{q_N}\right\}$. This is followed by a short explanation of that which has just been written.

17. Instructor-N writes that for all other points: $0\le f\left(c\right)\le \frac{\in }{2}$

18. A student asks for clarification on what has been written in events 16 + 17 and Instructor-N answers.

19. Instructor-N writes: “If we denote by ${\sigma }_1$ the Riemann sum of the problematic points, then: $0\le {\sigma }_1\le N\cdot M\cdot \lambda \left(P\right)$”.

20. Instructor-N says: “What can we control here? N and M are determined by epsilon, right? What I can control here is $\lambda$. It’s obvious we can take $\lambda$ to be so small that I could make this (pointing at ${\sigma }_1$) as small as I want. Now let’s see how small we need to make it in order for the entire Riemann sum to be smaller than epsilon.”

21. Instructor-N writes: “If we denote by ${\sigma }_2$ the Riemann sum for the rest of the points, then: $0\le {\sigma }_2\le \mathrm{\Sigma }{\mathrm{\Delta }}_i\frac{\in }{2}$”.

22. Instructor-N asks the students: “Why can I now write the following?”, and subsequently adds “$<\frac{\in }{2}$” at the end of the line written in event 21. A student answers correctly, to which Instructor-N replies “very good!”, and then explains the answer to the entire class.

23. Instructor-N explains that if we also make ${\sigma }_1$ to be smaller than $\frac{\in }{2}$, than the entire sum which is constructed of ${\sigma }_1+{\sigma }_2$ will be smaller than $\in$.

24. Instructor-N writes: “Meaning, if $N\cdot M\cdot \lambda \left(P\right)<\frac{\in }{2}$, or in other words $\lambda \left(P\right)<\frac{\in }{2NM}$, then: $\sigma ={\sigma }_1+{\sigma }_2<\frac{\in }{2}+\frac{\in }{2}=\in$”.

Appendix C.

Mathematical context for the KME in Lesson-N

We provide here an overview of the ideas needed for understanding the solution as it was presented in class. According to the Riemann definition for an integrable function, we need to prove that for all $\in >0$, there exists $\delta >0$ such that for any tagged partition $P$ whose mesh $\lambda \left(P\right)$ is less than $\delta$, we get that the Riemann sum $\sigma =\sum _{i=1}^{n}f\left(t_i\right)\mathrm{\Delta }{x}_i<\in$.

The solution required to split the sum into $\sigma ={\sigma }_1+{\sigma }_2$, each smaller than $\frac{\in }{2}$. If we make sure $f\left(t_i\right)$ is “small” in ${\sigma }_1$, meaning, $f\left(t_i\right)<\frac{\in }{2}$, then ${\sigma }_1=\hspace{0.17em}\sum f\left(t_i\right)\mathrm{\Delta }{x}_i\hspace{0.17em}<\frac{\in }{2}\sum \mathrm{\Delta }{x}_i\le \frac{\in }{2}\cdot 1=\frac{\in }{2}$. On the other hand, in ${\sigma }_2$ where $f\left(t_i\right)$ might be “big,” we require that $\mathrm{\Delta }{x}_i$ be “small.” How “small” we need $\mathrm{\Delta }{x}_i$ to be, will ultimately determine the choice of $\delta$.

Accordingly, we need to know for which $x$’s we obtain “big” or “small” values of $f\left(x\right)$. Given that $f\left(x\right)$ is either zero or a fraction in the form of one over a natural number, it is easier to compare its values to a fraction $\frac{1}{n}$ rather than the desired $\frac{\in }{2}$. Subsequently, if we choose $n_0$ such that $\frac{1}{n_0}<\frac{\in }{2}$, then we can evaluate $f\left(x\right)$ in relation to $\frac{1}{n_0}$. An analysis of this leads to the conclusion that for all $x$, except for a finite set of points, we have $f\left(x\right)\le \frac{1}{n_0}<\frac{\in }{2}$ (see Figure 4). While this is not a complete proof, we hope the explanation provides sufficient context for the identified KME.

Figure 4. A finite set of values larger than $\frac{1}{n_0}$.