Studying the role of human agency in school mathematics

Abstract

Mathematical discourse is often described as abstract and devoid of human presence, yet many school curricula espouse an aim to develop active, creative mathematical problem posers and solvers. The project The Evolution of the Discourse of School Mathematics(EDSM) developed an analytic scheme to investigate the nature of school mathematics discourse through the lens of high-stakes examinations in England. Following an overview of the scheme, this article ‘zooms in’ on the development of the sub-component addressing the question of how the origin of mathematical knowledge is construed, allowing investigation of the potential for students to see a role for themselves as active, creative agents in mathematical practices. Analytical tools operationalising this component are presented and their application illustrated. Results of analysis of examinations over a period of three decades suggest some increase in human agency, though some other aspects characteristic of higher-level mathematics may have reduced.

KEYWORDS:

• Examinations
• mathematical discourse
• discourse analysis
• agency

1. Introduction

In recent years, reforms to mathematics curricula and pedagogic approaches have tended to include statements of principles and practices that suggest philosophies of mathematics and mathematics education consistent with what Ernest (1991) styles a social constructivist theory of mathematics, “identifying mathematics as a social institution, resulting from human problem posing and solving” (p.281). For example, the National Curriculum for England starts by declaring:

Mathematics is a creative and highly inter-connected discipline that has been developed over centuries, providing the solution to some of history’s most intriguing problems. … A high-quality mathematics education therefore provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject. (Department for Education, 2013)

The Hong Kong curriculum states an aim to develop in students:

… the ability to think critically and creatively, to conceptualise, inquire and reason mathematically, and to use mathematics to formulate and solve problems in daily life as well as in mathematical contexts and other disciplines. (Hong Kong Special Administrative Region Government, 2015)

while the curriculum in the Australian state of Queensland encourages teachers:

 …  to help students become self-motivated, confident learners through inquiry and active participation in challenging and engaging experiences. (Queensland Studies Authority, 2013)

Values ascribed in curriculum documents to student characteristics such as creativity and curiosity and to activities such as inquiry and active participation seem aligned both with the idea that mathematics is a creative human activity rather than an autonomous, pre-existing set of facts and with the suggestion that students themselves should engage actively in a range of mathematical processes including decision-making, conjecturing, problem posing and other forms of reasoning.

Such statements, however, do not stand alone, but appear alongside further curriculum aims that suggest alternative perspectives on mathematics and on the types of activities expected of students. For example, pupils in England are also expected to develop “the ability to recall and apply knowledge rapidly and accurately” (Department for Education, 2013). “Knowledge” appears here as an independent entity to be recalled and applied rather than created and value is ascribed to reproduction of facts and procedures rather than to reasoning and creativity. Of course, aims that value reproduction of existing knowledge are not incompatible with aims that value creativity and it is reasonable to propose that they can be accommodated within a single curriculum. However, they reflect different aspects of mathematical activity and propose different roles for students as reproducers of pre-established knowledge and as active, curious and creative agents in mathematical problem posing and solving.

This article addresses the question of the extent to which school mathematics allows a place for human agency in the creation of mathematical knowledge. Of course, ‘school mathematics’ is a very broad construct, encompassing an enormous variety of contexts. I do not attempt to provide a definitive answer to the question but to discuss the development of a set of analytic tools for interrogating school mathematics texts and to illustrate the application of these tools to a single context: examinations at the end of compulsory schooling in England. I draw upon the discursive approach adopted and developed in the project The Evolution of the Discourse of School Mathematics (EDSM), which sought to investigate changes over time in the kind of engagement in mathematics expected of school students in England. In the next section I outline this approach and discuss how it conceptualises the issues involved in studying human agency in mathematics. I then present an account of the development of tools for its analysis in school mathematics texts and illustrate how these tools allow us to characterise single texts as well as the potential they allow for investigating differences across time.

2. Mathematics and school mathematics as discursive practices: where is human agency?

The EDSM project was founded in a theoretical conceptualisation of mathematics as a discursive practice (see Sfard, 2008). In other words, participating in mathematics consists of engaging in distinctively mathematical forms of communication, whether with others or in internalised communication with oneself. Fundamentally, this conceptualisation makes no distinction between content and form: there is no independent mathematical ‘content’ or ‘thought’ that is ‘expressed’ in language. Rather, communicating using mathematical language and other modes of communication such as algebraic notation, graphs and diagrams constitutes thinking mathematically and doing mathematics. Similarly, learning mathematics is conceived as developing ways of speaking and writing that are recognised as mathematical.

I have used the phrase ‘recognised as mathematical’ advisedly, indicating that mathematical practices are diverse and socially situated. Recognition may vary between contexts and according to the location of the authority to say that a form of communication is mathematical. The mathematical discourse encountered in a primary school is different from that in a secondary school classroom and this is different again from that engaged in by research mathematicians. Indeed, even these broad categories do not reflect the extent of variation. As Richards (1991) points out, research mathematicians participate at different times in discourses with distinct modes of argument. In much of their spoken mathematics they will speak “Research Math”, employing a “logic of discovery” that construes mathematical reasoning as a human activity, taking place over time. On the other hand, in most published writing they will make use of the discourse of “Journal Math”, depending on ‘reconstructed logic’ that construes mathematics as an autonomous and timeless structure of axioms, theorems and proofs. This oral/written distinction has changed over time, as shown by Solomon and O’Neill’s (1998) analysis of texts by the nineteenth-century mathematician Hamilton.

Solomon and O’Neill distinguish what they call “the mathematical text”, consisting of agentless statements of mathematical properties and relationships, from “a personal narrative” of the author’s process of mathematical discovery. However, this distinction reflects a view of the nature of mathematics that can be contested. I would argue that ‘mathematics’, understood as a discursive practice, includes not only the product of mathematical activity but also the processes that give rise to it and the values of the practice (Morgan, 2001). These processes of mathematical production may be construed as the autonomous action of mathematical objects (usually in the atemporal present tense), as in:

The functors H and K induce a duality … (research paper, anonymously cited in Burton and Morgan, 2000)

as agentless relationships or actions in which the agency is obscured, as in:

AB is the perpendicular bisector of OX

or

A perpendicular is dropped from A to OX

or as human material or mental actions as in:

Thus we introduce the non-dimensional coordinates and velocities (r, θ, z) … (research paper, anonymously cited in Morgan, 2001)

Who has the authority to recognise a given text or way of communicating as mathematical is dependent on the particular practice in which it is located and on the relationship of this practice to others and to wider social structures. Arguments about the school curriculum may often be understood as power struggles to assert authority over what may be considered ‘real’ mathematics. Examples of such struggles include the “Math Wars” in the US (see Schoenfeld, 2004) and critique of the use of ‘investigations’ in English schools in the 1990s (e.g. Wells, 1993). In both these cases, academic mathematicians challenged the types of student activity proposed by mathematics educators who were drawing on broadly social constructivist perspectives. The mathematicians used their authority within the discipline of academic mathematics as a means of challenging and attempting to devalue the expertise of mathematics educators.

The question of the origin of mathematics has long been a contentious issue within the philosophy of mathematics and among mathematicians themselves. In particular, Hersh (1997) characterises a dichotomy between formalist perspectives (adopted by philosophers such as Frege and Russell), which focus on axiomatics and logical deduction as the foundation of mathematics, and perspectives that see problem posing and human intuition as fundamental forces in the development of mathematics (Hersh’s own point of view). As noted earlier, the scholarly mathematical discourse that dominates the public practices of academic mathematics (Richard’s “Journal Math”) is characterised by the “reconstructed logic” of definition and deduction, consistent with a formalist perspective. This form of discourse proposes mathematical objects themselves and the relationships between them as the agents in the generation of new knowledge. However, just as in philosophical debates about the nature of mathematical discovery, the presentation of mathematical objects as the sole agents of mathematical development is not uncontested even in academic mathematics publications. Although modern research journal articles do not provide the kind of personal narrative found in Hamilton’s letters, human agency in narratives about the development of mathematics is also evident even in texts produced within the mainstream practice of academic publication of research mathematics. Burton and Morgan’s (2000) analysis of articles by research mathematicians revealed variation: while definition and deduction were clearly important constructs used in the construction and substantiation of narratives, other sources were also sometimes used. These included reference to the authors’ own expectations, problem posing or decision-making processes, sometimes explicitly based on analogies or intuitions, consistent with Hersh’s characterisation of mathematical processes. There were also articles that construed a human role in the formation of new mathematical arguments and theorems, arising from the author’s choice to use, or even devise, a particular form of definition and symbolism. Without devaluing the critical importance of the role of deduction in the construction of knowledge, these research mathematics articles also construed a space for human agency, especially in initiating and guiding the direction of enquiry.

Given the variation and contestation about the origin of mathematics and the role of human agency in its construction or discovery, together with the range of expectations for student mathematical activity expressed in curriculum documents, it is of interest to consider how the role of human beings in mathematics is construed in school mathematics texts. In this article, I am not concerned with the pedagogic roles and relationships construed for students and teachers (as seen in Herbel-Eisenmann and Wagner’s [2007] framework for examining student positioning in mathematics textbooks). Rather I am concerned with the extent to which mathematical facts and procedures are construed as products of human agency or as independently existing and self-generating.

There is nevertheless a pedagogical motive behind this interest. I am concerned with how students may relate to mathematics as a discipline and, in particular, whether they are able to see it as a human practice in which they may one day participate in an agentive, independent manner. The affective aspects of student participation, traditionally expressed in terms of ‘attitudes towards’ and ‘beliefs about’ mathematics, have long been a focus of research in mathematical education. Researchers have tried to find connections between attitudes and beliefs, on the one hand, and student achievement, on the other. A number of studies have focused on the phenomenon of disaffection, disengagement and alienation from mathematics (e.g. Lewis, 2013; Nardi & Steward, 2003). In recent years, this concern has been taken up by researchers working from discursive and postmodern perspectives who have focused on student identities in relation to mathematics (e.g. Heyd-Metzuyanim & Sfard, 2012; Klein, 2012; Solomon, 2012). In general, however, attitudes and identities have been related to pedagogic issues – styles of teaching and learning – and to public perceptions of mathematics, for example as a gendered activity (see Mendick, 2005), and not much attention has been paid in this context to the specific characteristics of the mathematical discourse in which students have been expected to participate. As mathematical discourse construes ways for human beings to relate to mathematical objects and processes, students may find it more or less possible to accommodate themselves to these relationships. In particular, the lasting experience of being a passive follower of other people or of an objectified discipline rather than an agentive participant in mathematical discourse may be a source of student disaffection.

3. Developing tools to characterise school mathematics discourse

In the previous section I asked whether the mathematics in which school students are expected to engage might be seen as a human practice in which students may (one day) participate in an agentive, independent manner. This question could be addressed by studying a wide range of sources, including classroom interactions and the many written texts used and produced by students. In the EDSM project we chose to investigate the examinations taken by students in England at the end of compulsory schooling. These examinations are used for public accountability purposes and have high stakes for students, teachers and schools. They thus have a strong influence on classroom practice and taking them as data provided us with a window onto the forms of mathematical discourse with which students in England were expected to engage, not only in the present day but also over a period of several decades.

We drew on Sfard’s (2008) communicational approach and on Halliday’s (1978, 1985) social semiotics and systemic functional linguistics (SFL) in order to develop textual indicators to interrogate the mathematics examination texts. Both these approaches are based upon an assumption that language does not represent some independent reality but is functional in constituting our experience of the world. In Halliday’s terms, our use of language performs ideational, interpersonal and textual metafunctions, realising (in the sense of ‘making real’) the field, tenor and mode of discourse. That is, the language we use construes the nature of the aspect of the world about which we are communicating, the social environment and relationships in which we are positioned and the type of communication and its role within the context. The grammar of SFL (Halliday, 1985) offers a comprehensive account of how lexicogrammatical characteristics of text serve these functions. (See Morgan (2006) for a discussion of the application of these constructs within mathematics education.) In developing a means of analysing mathematical text, we have used grammatical tools drawn from SFL alongside Sfard’s (2008) characterisation of mathematical discourse. SFL tools have been used previously in mathematics education to analyse various kinds of school mathematics texts by a number of researchers (including, for example, Chapman, 2003; Herbel-Eisenmann & Wagner, 2007; Morgan, 1998, 2005; O’Halloran, 2004; O’Keeffe, 2013). Although developed independently, the linguistic features that Sfard identifies are broadly compatible with SFL and offer the advantage of directing attention specifically to how they function in mathematical thinking (Tabach & Nachlieli, 2011). A fuller account of the theoretical and methodological basis of the EDSM project is given by Morgan and Sfard (this issue). In this article, I discuss the development of analytical tools to characterise the role of human agency in mathematics, starting with a broad overview of the structure of the analytic scheme developed in the EDSM project to characterise the discourse of school mathematics and then zooming in on those aspects of the scheme that address the issue of the origin of mathematical knowledge and the role of human agency within this. I will illustrate the evolution and application of the analytic approach with examples taken from the EDSM data set.

3.1. Structuring the analytic scheme

As a starting point, we identified two overarching aspects of the discourse of the examinations that interested us within the EDSM project as a whole. First, we wanted to characterise the forms of mathematical discourse that the examinations expected students to engage with, both as readers of the questions and as producers of acceptable answers. We also noticed at an early exploratory stage that examinations appeared to vary on another dimension: the amount of guidance provided to structure the student’s response or the amount of freedom they appeared to have to decide their approach to their answers. A second aspect of concern for our analysis was thus identified as the ways in which students were positioned in relation to the mathematics and the examination. In particular, we asked to what extent students were construed as independent decision-makers. Our analytic scheme thus needed to be structured according to these two aspects:

1. The forms of mathematical discourse in which students are expected to participate

2. Student relationships to mathematics and to the examination.

Under each of these headings, we developed more specific subsidiary research questions and, in interaction with our data, identified textual indicators that would enable us to have a systematic and reliable means of answering the questions.

The development of the subsidiary questions and textual indicators was an iterative process. Examples of examination questions from within our data set were inspected, allowing us to develop an informal sense of differences between them. This initial informal characterisation of differences was informed by knowledge of discursive characteristics identified in existing literature in linguistics and in mathematics education and led to drafting an initial set of questions about the text and textual indicators to enable us to answer each question. The indicators were then applied to further examples and the results scrutinised to see if they were successful in characterising distinctive features of the mathematical discourse of each question. This process in turn resulted in a refined set of indicators.

In this article, I provide a detailed account of the process of development of one part of the eventual analytic scheme. This account outlines the sources in linguistics and mathematics education research that informed this development and illustrates the iterative process of development of analytic tools in interaction with the data. The full analytic scheme is too extensive to address in full in this article so I zoom in on just one component, starting with the first aspect identified above, the forms of mathematical discourse in which students are expected to participate, identifying its components and illustrating the construction and refinement of textual indicators to characterise one element of this, namely the construal of the origin of mathematical knowledge. In considering the origin of mathematical knowledge, I am concerned with whether the generation of mathematical knowledge appears as dependent or independent of human action, thus opening up or closing down the potential space for human agency in school mathematics discourse. (Sfard [2008] identifies alienation, the discursive moves that obscure human involvement in mathematical activity, as a common and mathematically productive feature of mathematical discourse.)

This illustration offers a detailed exemplification of the process of development and of the structure of the scheme as a whole. The developed sub-set of analytic tools also provides a research tool that may have application beyond the EDSM project for addressing the issue of how the origin of mathematical knowledge is construed in school mathematics texts.

3.2. Zooming in on ‘the form of mathematical discourse’

The forms of the mathematical discourse in which students are expected to participate include both the texts that they are given to read and those that they are expected to produce as legitimate responses (either in the written examination situation that we were studying or in written and spoken texts produced in classrooms). A starting point for elaborating an analytic scheme was Sfard's (2008) characterisation of mathematical discourse consisting of four major components:

• Vocabulary and syntax – the words and the ways of combining them;

• Visual mediators – non-verbal modes of communication, including algebraic notation, graphs, diagrams, etc.;

• Routines – repeated patterns of discursive actions (e.g. steps in solving a type of problem);

• Endorsed narratives – those sequences of utterances that are taken to be true.

This characterisation of components of mathematical discourse is consistent with Halliday’s (1974) definition of the notion of mathematics register, consisting not only of vocabulary and grammatical structures but also of specialised forms of reasoning and argumentation. It is particularly well-suited to our purpose as it is specifically designed to answer the needs of an analysis of mathematical discourse, though we have also drawn on other sources, including those of SFL, to provide detailed textual indicators with which to interrogate the texts.

Taking these four components of mathematical discourse as an organising principle, we identified specific characteristics of the components, based on existing characterisations of mathematical discourse and on relevant issues in mathematics education found in the literature. For example, within the component ‘vocabulary and syntax’ we identified the following properties of mathematical vocabulary:

• Specialisation –the use of words that are either unique to mathematics or used in distinctive ways in mathematical contexts. This is one of the most easily recognisable characteristics of mathematical text. Pimm (1987), drawing on Halliday’s notion of a mathematics register, provides a comprehensive discussion of various types of specialised words, pointing out that it is often how a word is used that makes it mathematical rather than the word itself.

• Objectification – the naming of objects to enable a focus on properties of objects and relationships between them rather than on processes. Halliday (1993a) identifies this as a feature of much scientific discourse, while Sfard (2000) also discusses how it contributes to the formation of mathematical objects.

and of syntax:

• Grammatical complexity – grammatical devices such as complex nominal groups and repetitive or recursive use of subordinate clauses. Such constructions enable a lot of information to be packed into a single statement and are characteristic of much academic scientific writing (Halliday, 1993a)

• Logical complexity – explicit expression of logical relationships within and between statements. As well as using logical connectives such as if in specialised ways, as discussed by Pimm (1987), the dominance of reconstructed logic in Richard’s “Journal Math” discourse can be reflected in texts that are structured as arguments, like the following sequence taken from a research article, cited in Morgan (1998, p.17):

  But by (4), … . Hence, by (16), B = C. Then, by (4), (15) A = C (j²−j) = C. Hence … 

These properties of the discourse are related to subsidiary research questions contributing towards the overall research question about the properties of the mathematical discourse in which students are expected to participate. A summary of the discourse characteristics and subsidiary research questions is given in Table 1. This set of properties and questions is clearly not exhaustive. Researchers with different interests might identify a different set of properties and questions.

Table 1. Summary characteristics of the form of mathematical discourse.

Discourse properties	Subsidiary research questions to guide the analysis
Vocabulary
a. specialisation	To what extent is specialised mathematical language used?
b. objectification of the discourse	To what extent does the discourse speak of properties of objects and relations between them rather than of processes?
Syntax
c. grammatical complexity	How much ‘unpacking’ is needed to identify the mathematical information involved?
d. logical complexity	What kinds of logical relationships are present and how explicit are they?
Visual mediators
e. the presence of multiple modes of representation	To what extent does the discourse make use of specialised mathematical modes?
f. transitions between modes of representation	What transformations need to be made between different modes and are these provided or to be produced by the student?
Routines
g. the types of action demanded of students	What areas of mathematics are involved and what is the form of student engagement in these areas?
Endorsed narratives
h. the origin of mathematical knowledge	What is the degree of alienation of the discourse? To what extent is mathematics presented as a human activity?
i. the status of mathematical knowledge as absolute or contingent	To what extent does the text indicate that decisions or choices are possible during mathematical activity?

To provide an effective analytical tool, such broad categories and questions must be operationalised. In other words, we need to define indicators that allow us reliably to develop descriptions of our textual data. In the next section the development of the tool is illustrated as I turn to focus in detail on one aspect: the issue of the origin of mathematical knowledge.

4. How does a text construe the origin of mathematical knowledge?

The initial questions related to the origin of mathematical knowledge with which we addressed the data were:

	What is the degree of alienation of the discourse?
	To what extent is mathematics presented as a human activity?

These appear in the section of Table 1 under the heading “Endorsed narratives”, in this case addressing the kinds of statements that can legitimately be made about how mathematics is generated. In this section I elaborate and distinguish between these questions and identify and illustrate the textual indicators used to apply them to mathematical texts. Further questions and indicators arose during the analytic process. These are also discussed and illustrated, demonstrating how they led to refinement of the analytic scheme. Finally, I present the refined version of the scheme for investigating the origin of mathematical knowledge.

4.1. Alienated discourse

Sfard claims that alienation is a feature of mathematical discourse. She defines this term as the presentation of phenomena “in an impersonal way, as if they were occurring of themselves, without the participation of human beings” (Sfard, 2008, p. 295). Clearly, the degree of alienation found in a text contributes to the way it construes the role of human agency in the origin of mathematical knowledge. One discursive move identified by Sfard as contributing to alienation is the reification of mathematical processes and the use of the consequent reified objects as actors in subsequent processes. This not only transforms talk about processes into talk about objects but also discursively creates new objects that were not previously available to think about. More generally, ascribing agency to mathematical objects or to representational objects such as tables, graphs or diagrams rather than to human beings contributes to alienation.

The transformation of processes into objects is characteristic not only of mathematics but more generally of academic scientific discourse (Halliday, 1993a). It is not an arbitrary feature but is functional in that it enables complex phenomena to be assigned properties and to be put into relationships with one another. For example, by transforming a statement about a process such as the gradient of the function is changing into an object the change in the gradient of the function, we are able to produce further new objects such as the rate of change in the gradient of the function, and to say things about these objects such as the rate of change in the gradient of the function is positive (or increases as x increases or is given by the second derivative of the function, etc.) Linguistically, reification may be achieved by nominalisation (a grammatical metaphor that transforms a process such as rotate into an object rotation) or by coining new object terms that encapsulate mathematical processes. An example offered by Sfard (2008) is the object basic quadratic function, which she argues encapsulates the process of squaring.

A second linguistic source of alienation is the use of grammatical devices such as non-finite forms (infinitives, participles, gerunds) and passive voice that, while preserving a focus on processes as a part of mathematical discourse, obscure agency in those processes.

In summary, indicators of alienation in mathematical text, identified a priori before the start of data analysis were:

• Presence of reified mathematical objects;

• Objects as agents;

• Non-finite verb forms;

• Passive voice.

The example shown in Figure 1 illustrates several ways in which a high degree of alienation is achieved, summarised in Table 2.

Figure 1. East Anglian Examinations Board, London Regional Examining Board, University of London Examinations Board, Joint O Level/ CSE Examination, Mathematics Paper 4, June 1987.

Table 2. Discursive forms found in Figure 1 that contribute to alienation.

discursive form	how it contributes to alienation
Figure 2 shows	The figure itself is an agent, independent of any human creator. The presentation of representational objects such as figures, tables or graphs as agents in such communicative processes is a common phenomenon in the examination questions.
a tangent AT touching the circle The bisector of angle BAT meets the circle BP produced meets AT	The mathematical objects tangent, bisector, and BP are agents in material processes (touching, meets). Not only the objects themselves but also the relationships between them occur without human intervention.
BP produced meets AT	The non-finite form produced obscures the agency in the process. It is not apparent who or what decided to produce BP or carried out the material act.
Given also that AP = AQ	Again a non-finite form Given obscures agency, this time in the formation of the argument. Who or what ‘gives’ this information?

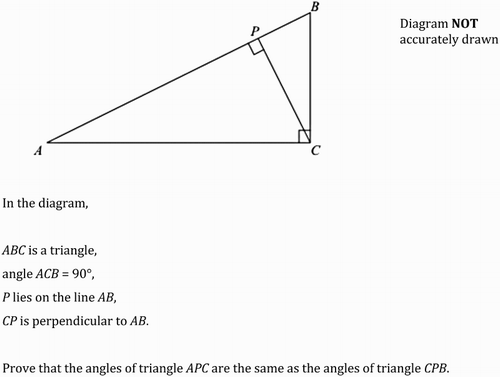
As we engaged with further examples within the EDSM data set, we noticed some questions that also seemed to obscure any human agency but which did so in a way that was not identified by our initial set of indicators. Through examining these questions, another discursive form emerged as a significant contributor to alienation: the extensive use of statements involving only relational processes – that is, statements about the properties and identities of objects rather than about actions (often involving use of the verbs to be or to have). Again taking an example from the domain of geometry, the question in Figure 2 presents a sequence of such statements.

Figure 2. Edexcel, GCSE Mathematics (Linear) 1380/3H, June 2011.

In Figure 1, the mathematical objects were involved in material processes – that is statements about doing (touching, meeting, producing) – construing mathematics as an active process, taking place in time. In contrast, in this case, the relational statements are atemporal. Mathematical objects and their properties just exist:

CP is perpendicular

angles of triangle APC are the same as … (emphases added).

The extensive use of relational processes is characteristic of much scientific writing and plays an important role in enabling some forms of scientific and mathematical reasoning. At the same time, however, it serves to conceal the activity that generates mathematics, construing “a world made out of things, rather than the world of happening – events with things taking part in them – that we were accustomed to” (Halliday, 1993b, p. 82).

It is interesting to consider how the information provided in Figure 2 might be written differently using forms similar to those used in Figure 1, for example:

The diagram shows a right-angled triangle ABC with the right angle formed at C. A perpendicular dropped from C meets AB at P.

Here a process of construction of the figure is evident – the right angle has been formed and a perpendicular has been dropped. While still an alienated form of discourse, the implications with regard to the nature and sources of mathematical objects are different in each of these two examples.

We thus chose to refine the subsidiary research questions guiding our analysis in order to make this distinction, asking not only:

What is the degree of alienation?

but also:

To what extent is mathematics construed as involving material processes or as atemporal objects and their properties?

This question may be addressed by investigating the categories of processes, focusing particularly on material (doing) and relational (identifying or attributing) processes. As exemplified in the question shown in Figure 1, representational objects such as tables, graphs and diagrams appear frequently as actors in verbal processes (such as show, indicate) – an indicator of alienation already identified in the analytic scheme. Mental and behavioural processes (such as consider, decide) can only be performed by sentient beings (though, in cases of metaphorical anthropomorphism, they may be ascribed to computers or other inanimate objects) and thus, unlike the other forms discussed in this section, immediately construe a role for human beings. See Halliday (1985) for full definitions and grammatical characteristics of process types.

4.2. Human activity

The notion of alienation is defined by absence or obscuring of human participation. In assessing the degree of alienation it is necessary to consider its opposite – the presence of an active human agent. A further question to guide our analysis is thus:

To what extent is mathematics presented as a human activity?

An obvious textual indicator of human activity is the presence of people, identified by a proper name, role descriptor (e.g. an architect or a student) or pronoun. Human activity is also implicitly present in questions or imperative instructions that indicate what students should do. The question posed here is at a general level, concerning the place of human beings in general, including, but not exclusively, students. The EDSM project data that provide the examples illustrating this article included very few instances of first or second person pronouns.¹ In applying the analytic tools to texts such as textbooks or classroom interactions, they would be likely to play a much more significant role (see Pimm’s (1984) discussion of the use of we).

In the question shown in Figure 3, for example, we may see involvement of the named Richard as well as of the student-examinee who is expected to draw, mark a point and respond to the question in part (iii). In this case, however, Richard’s participation is in a non-mathematical activity, even though a mathematical gaze is imposed onto his route (cf. Dowling, 1998). While the use of extra-mathematical contexts in the examination questions is of interest to us in the EDSM project, it is dealt with in another section of the analysis where we consider the extent to which the examinations use specialised mathematical discourse. Some results of the analysis of specialised mathematical discourse are presented in Morgan and Tang (this issue). In considering the component of the analytic scheme under discussion here, Richard’s presence does not contribute to presenting mathematics itself as a human activity.

Figure 3. OCR, GCSE Mathematics Syllabus A, Paper 4 (Higher Tier), June 2010.

It is possible to construe the student’s proposed activity as mathematical: constructing a diagram to represent a mathematisation of Richard’s journey. In the first and final parts of the question, however, the student is allowed some apparent freedom to choose how to determine the answers. Although the objects concerned (bearing, angle PXS) are specialised mathematical objects, the processes are left undefined. Here the nature of human involvement in mathematics is construed as focusing on “finding” answers without any indication of the mathematical processes that might enable this.

As shown in the case of the question in Figure 3, interaction with our data made it clear that simply identifying human participants in the text was not sufficient to distinguish them as mathematical actors. Moreover, even where human participants were identified as actors in mathematical processes, the nature of their mathematical activity emerged as a further factor of interest.

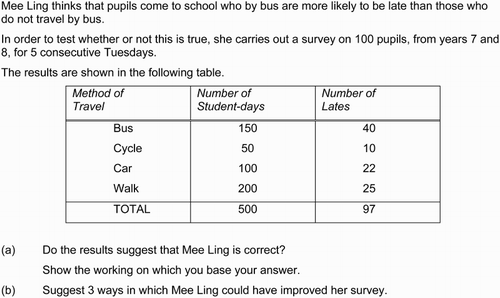
For example, the question shown in Figure 4 presents a human actor, “Imran”, in the mathematical processes of using a formula, calculating and estimating. These are examples of what Rotman (1988) styles “scribbling”, manipulation of symbols without any reflective or decision-making – “thinking” – activity. In this example, the student is also instructed to engage in “scribbling” activities: write down; work out the estimate; use your calculator. Rotman argues that thinking, as well as scribbling, is essential to the activity of a human mathematician, suggesting, therefore, that this example construes an incomplete version of human mathematical activity. Students are expected to engage in recalling and applying rather than constructing or creating knowledge.

Figure 4. London Examinations, GCSE Mathematics A/B – 1385/1386, Paper 6 (Higher Tier), June 1999.

Apart from very occasional instructions to students to “prove” or “explain”, the data set contains few references to human actors engaged in or directed toward processes that might be considered as mathematical “thinking”. The requirement to demonstrate reasoning as part of the examination process thus appears separate from the general construal of mathematical activity. Figure 5 shows one of the few exceptions. It is in the domain of statistics, a domain that our wider analysis suggests differs from others in several ways. Here, as in the previous example, the question starts by introducing a human actor, “Mee Ling”. On this occasion, Mee Ling thinks and acts to test her idea. By using the non-specialised term thinks instead of, say, conjectures, her engagement in a statistical investigation is construed, at least in part, as an everyday activity. Nevertheless, both Mee Ling and the student are construed as actors in “thinking” activities (think; test; base your answer; suggest) as well as “scribbling” (carry out a survey; show your working), thus construing a form of activity that conforms more to that of Rotman’s mathematician.

Figure 5. Midland Examining Group, GCSE Mathematics (without coursework), Paper 3 (Further Tier), June 1995.

4.3. Summary of analytic scheme for the origin of mathematical knowledge

In the previous sections I have illustrated how we developed the analytical tools for investigating how the origin of mathematical knowledge is construed in examination texts. Taking the subsidiary research questions identified at the beginning of the study (listed in Table 1) as our starting point, we looked in detail at a sub-sample of examination questions. This enabled us to refine the questions and to define specific indicators in the text. The fully developed section of the scheme is shown in Table 3. The complete scheme is presented in Morgan and Sfard (this issue).

Table 3. Complete analytic tool for characterising how a text construes the origin of mathematical knowledge.

Discourse property	Subsidiary research questions guiding the analysis	Textual indicators
the origin of mathematical knowledge	What is the degree of alienation of the discourse?	mathematical objects as agents in processes agency obscured by: non-finite verb forms passive voice
	To what extent is mathematics construed as involving material action or as atemporal objects and their properties?	mathematical objects involved in: material processes relational processes
	To what extent is mathematics presented as a human activity?	human agents in mathematical processes thinking scribbling

5. Example of analysis: identifying human agency in mathematical activity

In this section, I illustrate the application of the part of the analytic scheme developed above in order to begin to address the question posed in the EDSM project of how the mathematical discourse in which students in England are expected to engage has varied over the past decades of curriculum and examination reform. The analytic scheme may be used to produce detailed qualitative analysis of individual questions as illustrated earlier in this article. However, a principal aim of the EDSM project was to characterise variation over time, which cannot be determined by comparisons at the level of individual questions. A data set was thus constructed, comprising sets of examination papers from eight years from 1980 to 2011; the years were chosen purposefully in an attempt to capture variations that may have arisen from curriculum and policy changes. The principles for constructing the data set are presented in fuller detail by Morgan and Sfard (this issue). The complete text of all the examinations (excluding initial rubrics) was coded (assisted by nVivo software) using the textual indicators in the analytic scheme, enabling quantitative analysis of discursive properties of examinations set in each year. Further details of the coding procedure and results of analysis focusing on the degree of mathematical specialisation of the discourse are presented in Morgan and Tang (this issue). In what follows, I use the scheme presented in Table 3 in order to explore possible variation over time in how the mathematical discourse experienced by students taking the examinations construes the origin of mathematical knowledge. First, I examine the degree of alienation of the discourse, considering the presence of reified mathematical objects and the extent to which agency may have been ascribed to human beings or to objects. I then examine whether the examinations have construed mathematics as being about actions or about properties and relationships by looking at the proportions of material and relational processes.

Presence of reified mathematical objects. The details of the analysis of reification are reported in Morgan and Tang (this issue) as this indicator is also included in the part of the analytic scheme addressing the degree of specialisation of the discourse (as mathematical rather than colloquial). To summarise the results, we found that, while students were expected to engage with similar numbers of reified mathematical objects throughout the time period of the EDSM data set, there was a decreasing trend in their density within the text: examination papers from the more recent years contained fewer reified mathematical objects per question.

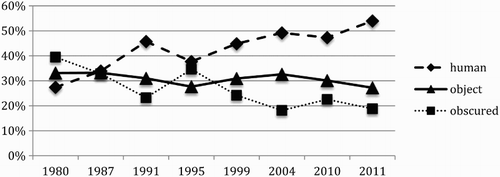
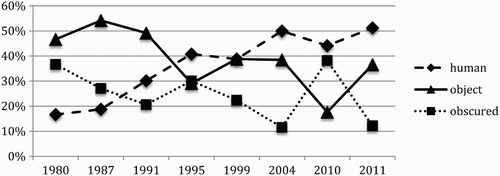
Agency: human/object/obscured. Each non-relational process was coded according to the type of agency ascribed to it: was the agent a human actor, was it an object or was agency obscured by the use of a non-finite verb form or passive voice? The proportions of each type of agency across the years of the EDSM data set are shown in Figure 6. There seems to be an increase in the proportion of human agency, suggesting a reduction in alienation. Comparisons of proportions of human agency in Table 4 show that 1980, 1987 and 1995 were significantly lower than most of the later years. We wondered whether this might be accounted for by the increase in questions involving non-mathematical contexts with human actors as agents in non-mathematical processes (like Richard in the question in Figure 4). Further analysis was therefore done, examining agents in specialised mathematical processes only. The results are shown in Figure 7 and Table 5. Interestingly the upward trend in human agency appears more marked when we look only at specialised mathematical processes, with a strong disparity between 1980 and 1987 and later years. When we consider only specialised processes, the proportion of these with human agents in 1995 no longer stands out as significantly lower than later years. These figures do not include imperatives instructing students to perform processes, suggesting that there may be an increase in questions that include narratives of human beings engaged in mathematical activity, like Mee Ling’s survey in Figure 5 above. Informal scrutiny of a selection of such questions suggests that a high proportion of them, like Figure 5, involve statistics or probability. Further analysis is required to investigate whether the apparent increase in human agency in mathematical processes is associated mainly with the increasing curricular emphasis on handling data in England over the time period studied or whether it is also evident across other topic areas.

Figure 6. Types of agency in processes found in examination papers.

Figure 7. Types of agency in specialised school mathematics processes.

Table 4. Proportions of all processes having human agency.

	% of all processes having human agency (%)	Z-scores
		1987	1991	1995	1999	2004	2010	2011
1980	27	-1.4147	-3.7544**	-2.2672*	-3.3675**	-4.1262**	-3.7836**	-5.0546**
1987	34		-2.8640**	-1.0009	-2.4236*	-3.3263**	-2.9209**	-4.4273**
1991	46			2.0306*	0.1946	-0.7252	-0.3276	-1.7653
1995	38				-1.6324	-2.5828**	-2.1601*	-3.7243**
1999	45					-0.8510	-0.4822	-1.8136
2004	49						0.3645	-0.9391
2010	47							-1.3087
2011	54

Two-tailed Z-test, *p < 0.01, **p < 0.05.

Table 5. Proportions of specialised mathematical processes having human agency.

	% of specialised processes having human agency (%)	Z-scores
		1987	1991	1995	1999	2004	2010	2011
1980	17	-0.3299	-1.7620	-3.1851**	-2.7638**	-3.7671**	-2.8943**	-3.6973**
1987	19		-1.6652	-3.3834**	-2.8380**	-3.9708**	-2.9207**	-3.8567**
1991	30			-1.3770	-1.0357	-2.1699*	-1.3748	-1.3748
1995	41				0.2563	-1.0926	-0.3427	-1.1400
1999	39					-1.2211	-0.5137	-1.2628
2004	50						0.5340	-0.1168
2010	44							-0.6128
2011	51

Two-tailed Z-test, *p < 0.01, **p < 0.05.

Material and relational processes. Proportions of statements involving material (doing) processes and those involving relational processes, ascribing properties or asserting identities, remained fairly stable across the time period with no discernible trend. Material processes varied between 54% and 61% of all processes, while relational processes varied between 17% and 25%. This suggests that, in each of the years studied, students were expected to engage with a varied mathematical discourse, involving both material actions by and on mathematical objects and statements about the properties of objects and relationships between them. The difference identified above between the two geometry questions in Figure 1 and Figure 2 suggested to us that there might be changes in the discourse within specific topic areas. Analysis of just the questions within the Shape and Space area of the curriculum again showed no discernible trend in the proportions of material and relational processes, with material processes varying between 47% and 57% of all processes, while relational processes varied between 21% and 33%. It may be that there are differences between specific topics within this curriculum area (e.g. circle theorems or transformation geometry). However, at this level of specificity, the number of questions on each topic is too small (generally no more than two or three questions per topic per year) to be able to draw conclusions using the EDSM data set.

6. Conclusion

My focus in this article has been on studying the extent to which school mathematics discourse includes a role for human agents in doing mathematics. This focus attends to the onto-epistemological aspects of the discourse – considering the nature of mathematical objects, mathematical knowledge and its origins in general, rather than the specific roles that the discourse may propose for students as participants in school mathematics. The set of analytical tools developed, discussed and utilised here thus excludes those that have a direct interpersonal function, construing student roles in mathematical activity and their relationships to mathematics, to the examination and to the examiners, such as uses of imperatives, personal pronouns and positive or negative modality. Having said this, it was argued at the beginning of this article that general narratives about the origin of mathematical knowledge and the nature of mathematical activity also make available possible ways for students to relate to mathematics. If mathematical discourse lacks involvement of human agents and is highly alienated, involving statements about properties of objects and relationships between objects rather than about material or mental processes, it is likely to be harder for students to construe a present or future role for themselves within that discourse as active and creative participants.

The quantitative analysis of examination papers over a period of three decades suggests an increase in the incidence of some of the textual indicators for human agency. In particular, the degree of reification has decreased and the proportion of human agency in all processes, including specialised mathematical processes, has increased. On the other hand, there has been no discernible quantitative change in the use of relational statements that might serve to construe mathematics as being about properties of mathematical objects and relationships between them rather than about material actions. These results suggest that there has been some movement in the discourse of school mathematics examinations towards operationalising the kinds of aims evident in the curriculum extracts cited at the beginning of this article: providing a space for students to construe a role for themselves as human participants in mathematical activity.

When considering change, it is important to consider not only what may have been gained (in this case, alignment with a particular set of curricular aims) but also what may have been lost (cf. Kress, 2005). As discussed above, conventional academic mathematics discourse, especially the high status “Journal Math” (Richards, 1991), is highly alienated. Even when human agency is afforded a role within academic mathematics texts, as in some of the texts studied by Burton and Morgan (2000), the discourse also involves reified mathematical objects, their properties, and relationships between them. Indeed, through reification, new mathematics is generated: new kinds of statements about new mathematical objects, new properties and relationships become possible (Sfard, 2008). If changes to school mathematics discourse increase human participation at the expense of a reduction in reification there is a risk that students will be less well prepared to progress to higher level study of mathematics. The results of the EDSM project are inconclusive on this point. They indicate that the gross number of reified objects that students are expected to engage with in examinations has not changed although the number of distinct such objects within single questions has fallen (Morgan and Tang, this issue). Possible effects of this change on student preparedness have yet to be investigated.

As is often the case, the results presented in this article raise further questions. It seems possible that some of the changes in school mathematics discourse as reflected in examinations are related to changes in the topics included in the curriculum rather than reflecting a more general change in its onto-epistemological orientation. In particular, the increased emphasis on data handling in the curriculum in England since 1988 may be related to increased measures of human agency; examination questions in this topic may be more likely to involve narratives about people doing statistical investigations. The tools provided by the EDSM analytic scheme would enable a study of differences between various areas of the curriculum but this would require a different kind of data set, allowing the researcher to zoom in on more substantial sub-sets for specific topics. The EDSM project chose to use examinations as a window onto school mathematics discourse because this allowed us to construct a data set to investigate change over time. While I have argued that the view through this window gives an important insight into the mathematical discourse that school students are expected to engage with, it is also evidently a restricted and partial view.

In this article, I have presented some of the results of the EDSM analysis of school mathematics examinations but have also provided an account of the development of one part of the analytic scheme. This scheme makes use of tools from SFL that may be applied to any text and, by also drawing on Sfard’s characterisation of mathematical discourse, is designed to highlight features that are particularly significant in mathematical texts. As described here, the scheme was developed in interaction with our data set. This enabled us not only to ensure that textual indicators were defined clearly enough to be operationalisable but also to observe, define and add to the scheme further textual characteristics that seemed interesting and relevant to our study. The analytic scheme presented in this article (and in full in Morgan and Sfard, this issue) may thus be seen only as a starting point for further studies of school mathematics discourse. Further study of the role of human agency in school mathematics would be enhanced by using a wider range of data sources, including for example textbooks and digital resources, enabling a fuller picture of the mathematical discourse that students are expected to participate in. Interaction with different types of text may well lead to adaptation or augmentation of the analytic scheme to take account of such different genres.

Acknowledgements

The examination questions shown in Figures 1, 2 and 4 are included by kind permission of Pearson Education Ltd.

The examination questions shown in Figures 3 and 5 included by kind permission of Oxford Cambridge and RSA (OCR) Examinations.

Additional information

Funding

The EDSM project was funded by the Economic and Social Research Council [grant number ES/1007311/1].

Notes

1. The pronoun you was found in general rubrics instructing students how to engage with the examination process (e.g. You must show all your working) but these parts of the examination texts were excluded from the analysis of the form of mathematical discourse.