The positioning of GCSE and Functional Skills in Further Education: how do vocational students make sense of post-16 mathematics pathways?

ABSTRACT

Continuing to study mathematics is currently a requirement for low attaining 16- to 18-year olds in Further Education, as part of an ongoing drive to raise basic numeracy skills in England. However, these students, widely regarded as demotivated, often fail to make any progress in mathematics over the two years. This research explores how students make sense of the complex relationship between the two main post-16 qualifications, GCSE and Functional Skills, and its effect on students’ opportunities to succeed in mathematics. The study was conducted with vocational students (N = 187) at one Further Education college in the academic year 2018–19, using both a questionnaire and examination results. Findings suggest multiple dimensions that students valued in mathematics qualifications, while GCSE and Functional Skills were viewed either as a single linear progression or as two divergent pathways. Success was linked to features of the qualification taken, raising questions about inequality of opportunity.

KEYWORDS:

• Post-16 mathematics
• vocational mathematics
• use and exchange value

Introduction

This paper addresses the pressing question of how to provide appropriate pathways for vocational students learning mathematics. While adding, reforming, and repurposing qualifications is usually seen as unproblematic, this paper argues that the relative positioning of mathematics qualifications is central both to students’ experiences and to their opportunities for success. In developing this argument, I will first outline the current policy situation for vocational students in English Further Education (FE) colleges, exploring the ways in which variations on a “journey” metaphor are used to explain the somewhat confusing maze of pathways through qualifications. Secondly, the research approach is discussed, focusing on how students understand and explain the relationship between post-16 mathematics qualifications. The third section presents the research findings in the form of an alternative set of journey metaphors intended to capture the perspectives of students studying Functional Skills and GCSE mathematics alongside their main vocational qualifications, and hence to shed light on the metaphors used by policy makers and practitioners. The fourth and final section discusses the implications of these different perspectives, concluding by drawing together some important considerations for future policy shifts and qualifications reform.

Context

Despite the widely varying structures and forms taken by vocational education in different countries (Bakker, 2014) the issue of what mathematics vocational students should learn, and in particular the tension between workplace and academic mathematics, is a matter of concern internationally (e.g. FitzSimons, 2014; Lindberg & Grevholm, 2013). In his 2004 report, Smith sought to resolve this tension by calling for the joining up of UK mathematics qualifications into “a highly flexible set of interlinking pathways that provide motivation, challenge and worthwhile attainment across the whole spectrum of abilities and motivations” (p. 8). The need for such a set of pathways is more pressing than ever, given the current political drive towards young people studying mathematics for longer, alongside increased participation in education to 18 (Department for Education [DfE], 2016). A key study by Hodgen, Pepper, Sturman, and Ruddock (2010) described the UK as “out on a limb” as one of the few nations where mathematics was entirely optional for 16- to 18-year olds. The most common approach among the 24 countries studied was for the mathematics requirement to be dependent on the type of education (general or vocational). However, the UK has since adopted a model comparable to New Zealand’s minimum numeracy requirement, placing the focus on ensuring a minimum level of basic skills. The new condition of funding for England, introduced in 2015, requires 16- to 18-year olds remaining in education to continue to study mathematics unless (and until) they have achieved at least a grade 4 (or old grade C) in GCSE mathematics (Education & Skills Funding Agency [ESFA], 2014–2020). This affects just over a third of the cohort each year (Office of Qualifications and Examinations Regulation [Ofqual], 2014). While the policy is not aimed specifically at vocational education, this is where the greatest impact is felt. These lower-attaining students predominantly go on to study vocational qualifications at the age of 16 rather than the more academically demanding A-levels, and attend FE colleges rather than sixth forms (Smith, 2017).

The question of what mathematics these low-attainers should study remains underexplored. As FitzSimons (2014) notes, “there appears to be a tendency for many official documents to use terms such as basic mathematics without elaboration, on the assumption that there is a shared and unambiguous meaning” (p. 297). Without getting into the details of specific mathematical topics, one approach is to describe mathematics in terms of its use value and exchange value (Williams, 2012). That is, the mathematical skills and competencies which will be of practical use in the future, compared to the mathematical qualifications which can be “exchanged” for future benefits such as access to higher education and jobs. While on the one hand there have been attempts to strengthen links between mathematics curricula and genuine workplace practice (Wake, 2014), at the same time attempts to formalise informal vocational knowledge via qualifications have the tendency to lead to “academic drift” (Muller, 2009). Indeed, Pais (2013) argues that perhaps mathematics is important “not because of its characteristics – problem-solving, utility, beauty, cultural possibilities, etc. – but because of the sociopolitical importance assigned to it” (p. 16), aligning with the Bourdieusian view of mathematics as a form of cultural capital (Williams, 2012). From this point of view, the contents of the mathematics curriculum are relatively inconsequential compared to the weight attached to the title of “mathematics”.

In the context of Further Education in England, the tension between use and exchange values is evident in the relationship between the two main qualifications available to students: the General Certificate of Secondary Education (GCSE) and Functional Skills (FS). In the recently completed Mathematics in Further Education Colleges Project (Noyes & Dalby, 2020) students generally viewed GCSE as having high exchange value but low usefulness in terms of the mathematics learned, in particular not providing “vocationally-related skills” (p. 31). GCSE was also a means to be “released” from having to take mathematics again in the future. In contrast, in her substantial work with students taking FS, Dalby (2012, 2013, 2015) has consistently found evidence for the effectiveness of the functional curriculum in motivating and engaging students through presenting “a new image of mathematics as a useful ‘tool for life’” (Dalby, 2015, p. 3), although this sits in tension with the lower perceived exchange value of FS as a qualification. Thus, while the Education & Training Foundation (ETF) has highlighted the need for students “to understand the relevance, purpose and importance of the maths … they are studying” (2015, p. 13), it appears to be difficult in practice to achieve all of these goals within one post-16 qualification.

In addition, the current condition of funding has resulted in both a repurposing and repositioning of these mathematics qualifications. The current use of GCSE diverges from its intended purpose as a single qualification to be taken by all students at age 16, allowing the full ability range to be measured against a common framework (Butterfield, 1998). GCSE grade C had already been increasingly viewed as a “gold standard” (Dalby, 2015) and the devaluing of lower grades was consolidated under the reformed GCSE introduced in 2017, with the new grade 4 (aligned with the old grade C) labelled a “standard pass” (DfE, 2019), implying that grades 3 and below constitute a fail. As a result, the grade 4 boundary is now, to use Bourdieu’s (1998) words, “a true magical threshold separating the last candidate to have passed from the first to have failed, instituting a difference in kind” (p. 21). This difference in kind is evident in the greater educational and employment options available to students who narrowly pass their GCSE compared to those who narrowly fail, a difference of only a few marks (Machin, McNally, & Ruiz-Valenzuela, 2018). However, passing this threshold appears unobtainable for many resit students, who have already failed once at age 16. For the most recent cohort, only 29% went on to achieve level 2 (i.e. GCSE or equivalent) by the age of 19 (DfE, 2020a) and, on average, students finish with a lower grade score than they started with (Groot, Sanders, Rogers, & Bloomenthal, 2017). Thus, since the repositioning of GCSE as a post-16 qualification as well as a secondary certificate, the devaluing of the lower GCSE grades has left a gap for a meaningful qualification for the lowest attaining students.

This is where Functional Skills comes in. Originally intended as an “alternative route” to learning mathematics, FS was designed for vocational students and is centred around practical applications in real-world scenarios (ETF, 2015). Instead of grades, students are entered at one of five levels (from low to high: entry 1/2/3, level 1/2), corresponding to UK qualification levels (Gov.UK, n.d.). A pass at FS level 1 is notionally equivalent in difficulty to GCSE grades 1 to 3, and FS level 2 equivalent to GCSE grades 4 to 9. This is borne out in their assessments, with FS level 2 papers being of comparable difficulty to higher tier GCSE questions (Barmby & Wheadon, 2019), although with reduced content. However, under the compulsory mathematics requirement introduced in 2015, students with a GCSE grade 2 (E) or below can take FS as a “stepping stone” to GCSE (ESFA, 2014–2020). This repositioning of FS as a lower qualification, rather than an alternative pathway, appears to repeat and reinforce the historically low status of vocational education compared to academic routes (Dalby & Noyes, 2016).

Changes to policy and curriculum since the study took place have not clarified the relative positions of GCSE and FS. On one hand, since September 2019 students achieving FS level 2 can also stop studying mathematics (ESFA, 2014–2020). This move reinstates FS as an alternative route to GCSE at least in terms of the condition of funding, although it remains to be seen whether this will lead to its greater acceptance as equivalent in exchange value, for example for university entrance. At the same time, FS qualifications have been reformed to be more closely aligned to the academic GCSE, for example through the introduction of a non-calculator element (DfE, 2018), reinforcing the linear view of FS as preparation for GCSE.

As a result, there appear to be two persistent and conflicting versions of a journey metaphor (Noyes, 2006) used to describe post-16 mathematics – the linear “stepping stone” metaphor and the parallel “alternative routes”. Both have been used by practitioners and policy-makers to explain the mathematics pathways available to low-attainers. This research, however, seeks to explore how students themselves explain and make sense of these qualifications. Examination outcomes are included as being a core part of students’ experiences, as well as critical to the next steps in their “journey”. In addition, this study aims to shed light on what students value in the qualifications themselves, beyond how this is currently organised and structured. This research therefore addresses the following three questions:

1. How do vocational students understand the relationship between GCSE and FS?

2. How do students’ experiences of success and failure in mathematics relate to these understandings?

3. What do students value in post-16 mathematics qualifications?

In the next section, I will discuss the approach taken to address these research questions within one particular FE college, not as a representation of all colleges but in order to illustrate how qualification positioning can impact on the ways in which students navigate through vocational mathematics.

The research

This study was conducted within a large, multi-site FE college in the South West of England. College sites differed in the numbers of students and the types of vocational courses offered but were centrally managed. The data were collected on the largest of these sites, which offered a wide variety of vocational courses across levels 1–3. In the academic year 2018–19 when these data were collected, there were around 1000 students enrolled on mandatory 16–18 mathematics courses (either GCSE or FS) across the whole college, although the exact number is hard to pin down due to students dropping out, and sometimes enrolling, mid-year. Included in the study were students aged 19–25 with an Education, Health and Care Plan (EHCP) recognising their learning difficulties or disabilities, who were subject to the same compulsory mathematics requirement as 16- to 18-year olds. A-level mathematics and adult classes comprising students aged 19 and above who enrolled voluntarily were not included. For students on compulsory courses, the qualification taken was determined by their prior attainment and, for some students, an externally produced diagnostic mathematics test known as bksb. Those in GCSE classes had either a prior grade 3 (or D) at GCSE or had passed FS level 2. All other students were entered for FS, with their level of entry being decided either by their attainment on previous FS courses or, for new students, their scores on the diagnostic assessment. There was, however, some flexibility, as students could be moved between levels during the course of the year based on teacher recommendations.

Questionnaires were conducted in all mathematics classes timetabled at the central college site across three days during February and March 2019, resulting in a total sample of 187 students (roughly 20% of the college cohort) all of whom explicitly consented to the use of their data for research purposes. Of these, 133 also agreed to the use of their end-of-year examination results. Conducting questionnaires in the classroom resulted in a high response rate, although it also introduced potential bias by only including students that were present on that day. Each class was only visited once in order to minimise disruption to learning and because additional visits would likely have resulted in only a few additional participants. Amongst many possible reasons for students being absent, some may have deliberately opted out of mathematics by not attending the lesson and hence some of the more negative student perspectives may be missing from the data. Addressing this bias would have required specific targeting of non-attending, and potentially truanting, students, which is clearly a highly sensitive area and beyond the scope of this study.

In addition to demographic questions (gender and age), students were asked to rate their current course on a 5-point Likert scale for four attributes: appropriate level of difficulty, relevance to their main vocational qualification, usefulness for everyday life, and importance for their future career, these being potential reasons for post-16 mathematics study suggested by the literature. Student outcomes for GCSE and FS were recorded as both a numerical mark and a binary pass or fail outcome. FS are not graded, with students receiving a pass/ fail result at the level for which they had been entered (in this case: entry 3, level 1 or level 2). GCSE grades 4 and above were counted as a pass and grades 3 and below as a fail, in line with the condition of funding. Given the limitations of the sample, exploration of the quantitative data focused on frequency analysis.

Participants were also asked to describe the main differences between GCSE and FS, state which qualification they would prefer to study, and give reasons for their choice. While this “choice” is unavoidably hypothetical, it serves to expose the aspects of GCSE and FS most important to students. As questionnaire data were only collected at one time point, they provide a snapshot, rather than a complete, long-term picture, which nevertheless gives some valuable insights into students’ perspectives midway through their one-year long mathematics courses.

These qualitative responses were analysed thematically, using metaphor as an analysis tool that “demands the interpreter becomes actively involved in searching for meaning” (Ashton, 1994, as cited in Noyes, 2006, p. 900). Thus, where previous mathematics education studies have asked participants to generate metaphors (Noyes, 2006; Schinck, Neale, Pugalee, & Cifarelli, 2008), here the production of metaphors was part of the analysis. Data were coded openly and grouped into themes, and then metaphors sought to capture these themes. Clearly, other metaphors could have been used, just as different themes could have been highlighted. It is hoped that the use of metaphor here draws attention to the subjective and personal nature of qualitative analysis, as well as enabling comparison with the journey metaphors already widely used for post-16 qualifications.

Findings

Student characteristics, attitudes, and outcomes

Among questionnaire respondents (N = 187), the largest age group was 17-year olds (31%) and almost 3 in 5 participants were female (58%), as shown in Table 1. Just over half of students (51%) were currently studying GCSE mathematics, while those on FS were predominantly taking one of the lower levels: either entry 3 (16%) or level 1 (20%).

Table 1. Student characteristics.

		Number	%
Gender	Male	66	35.3
	Female	108	57.8
	Other/ not specified	13	6.9
Age	16	42	22.5
	17	58	31.0
	18	47	25.1
	19+	32	17.1
	Not specified	8	4.3
Current maths qualification	Functional Skills Entry 3	30	16.0
	Functional Skills Level 1	37	19.8
	Functional Skills Level 2	19	10.2
	GCSE	95	50.8
	Not specified	6	3.2
	Total	187	100.0%

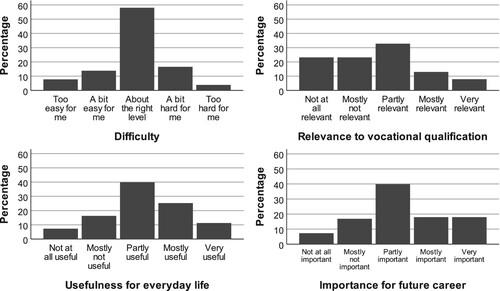
Based on the Likert scale questions, shown in Figure 1, students generally viewed their current qualification as being about the right level of difficulty. The majority described studying mathematics as at least partly useful and important, but generally not as relevant to their vocational course.

Figure 1. Attributes of mathematics qualifications (all qualifications).

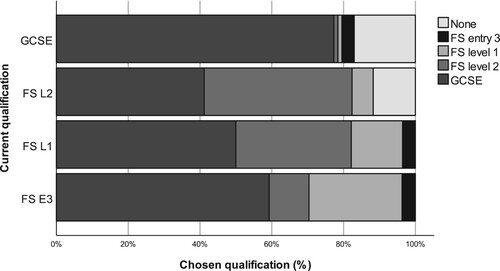
In addition, students were asked which qualification they would prefer to take, if given the choice. There was a notable preference for GCSE (58%) over Functional Skills (all levels – 21%) and an overall trend towards choosing higher qualifications (see Figure 2). Students on FS entry 3 were more likely to choose GCSE than those on the higher levels of FS. GCSE students were very likely to choose GCSE, whereas those on FS level 2 were equally divided between GCSE and FS level 2. Those on higher qualifications were most likely to say they would prefer not to study mathematics at all, although this was only 9% of the sample.

Figure 2. Students’ current and chosen qualifications.

Of the students who agreed to the use of their examination data (N = 133), 45% passed their mathematics qualification by the end of the academic year. The GCSE pass rate within the sample (32%) was slightly lower than that of the college (38%), as shown in Table 2. This suggests that excluding students absent from class on a particular day did not bias the sample as much as might be imagined, since it would be reasonable to expect that persistently absent students would be less likely to pass, reducing the overall pass rate. Both the college and sample GCSE pass rates were an improvement on the national data for GCSE resits (17%). This may have been due in part to differing policies on which students are entered for GCSE within FE colleges, for example some colleges enter students with a previous grade 2 as well as those with grade 3.

Table 2. Examination pass rates by qualification.

Mathematics qualification	FS E3	FS L1	FS L2	GCSE
Sample pass rate, 2019	95.0%	50.0%	33.3%	31.9%
College pass rate, 2019	–	–	–	38.3%
National pass rate, 2019	94.0%	65.0%	56.7%	17.3%

Note: National data from DfE (2020a, 2020b). Dashes represent unavailable data.

The relationship between GCSE and FS

While students did not have a unified view of post-16 mathematics qualifications, there was a clear sense of moving through and between qualifications over time, suggesting the continuing relevance of the overall journey metaphor. In particular, three metaphors are proposed as illustrating the distinctions between students’ perceptions – a race, a fork in the road, and a non-journey. These viewpoints are not presented as static, but as positions which students move between and may even sometimes hold simultaneously.

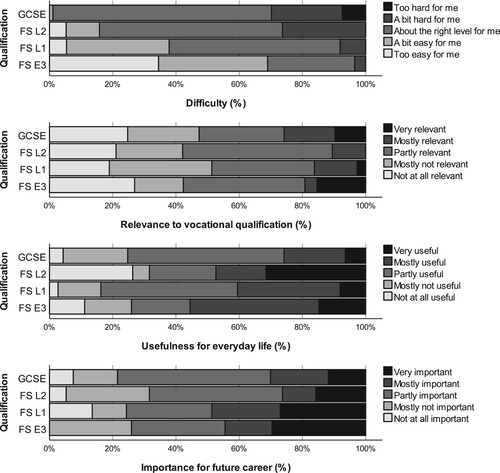
The first metaphor of a race describes a linear relationship where the journey is not only about progressing from one level of mathematics qualification to the next, from FS to GCSE, but also reaching the finish line in the shortest possible time. Students frequently described the differences between qualifications in terms of either difficulty (harder/ easier) or level (higher/lower), or sometimes both. While most students saw their current course as being about the right level, this varied between qualifications, as shown in Figure 3. Although students were placed on qualifications based on their prior attainment, it appears that they did not always agree with these assessments of the right level for them to take, with FS entry 3 students, in particular, seeing their course as too easy. The increasing difficulty was linked to a sense of chronological order, with “Functional Skills first” (Female, 17, GCSE). While some students were prepared to take on the challenge of higher/ harder levels straight away, others were aware of the need to prepare for GCSE.

There are some basic aspects of maths that I struggle to understand but I feel as though I am capable of GCSE. (Female, 16, FS E3)

It [FS L2] is the level that I am on so that I am ready and prepared for GCSE maths. (Female, 18, FS L2)

Figure 3. Attributes of mathematics courses by qualification.

Passing GCSE was seen as the finish line after which you no longer had to study mathematics, with the consequence that FS students had a greater distance to travel. This could explain why FS entry 3 students tended to prefer GCSE (see Figure 2), as they had the longest race ahead of them.

With Functional Skills, you have to do the subject the next year whether you passed or not. GCSE gives you the chance to not do it next year. (Male, 17, GCSE)

I want to be done with it for once. (Male, 18, FS E3)

In contrast, in the second metaphor there is no direct progression between FS and GCSE and no universal finish line. Instead, the relationship is divergent, comparable to a fork in the road where you must choose between different routes (mathematical content) leading to different destinations (the value of the qualification). The mathematical content of FS was acknowledged to be useful for everyday life, whereas the GCSE curriculum was seen as either not useful at all or as only useful for certain careers and certain areas of further study (including science and A-level mathematics). GCSE was less likely than all three levels of FS to be rated “very” or “mostly” useful for everyday life (see Figure 3). However, there was also a smaller proportion of students than for, say, FS level 2 who rated GCSE as “not at all useful”. It could be that the ideas of “usefulness for life” and “usefulness for certain jobs” had become conflated in these scores. Similarly, it is interesting that FS level 1 and entry 3 students tended to describe their course as more important than those on FS level 2 or GCSE courses, perhaps because they felt that having a grasp of basic mathematics would be important in any job whereas higher-level topics such as algebra are only needed for certain careers. Fortunately, the distinction is clearer in students’ written responses.

Functional Skills teaches you maths that helps you live in the real world and be independent. Whereas GCSE maths is topics that will help you if you want to pursue a maths based career. (17, GCSE)

GCSE maths is mainly based through remembering a list of different formulas, equations and a lot of other related factors but I'm guessing Functional Skills is not any easier but maybe teaches more appropriate matters used within day to day. (Female, 18, GCSE)

Whereas the value of FS was day to day utility, GCSE was overwhelmingly seen as opening future opportunities. For some students this was quite a general idea of GCSE being respected and recognised, particularly by universities and employers, while others had specific goals in mind, such as being able to progress from level 2 to level 3 of their vocational course.

Because it [GCSE] will look better on my CV and make it easier to get a job in the future. (Male, 18, FS L2)

If I take GCSE it would be easier to choose options for various universities and I will not be laughed at. (Female, 18, FS L1)

Notably, these two routes were seen as mutually exclusive alternatives; no one suggested that taking first FS and then GCSE might be a means of achieving the benefits of both.

A third view was that GCSE and FS are indistinguishable for all practical purposes, that is, “they are the same qualifications – there is no difference” (Male, 18, FS L2). The journey metaphor appears to fall down here as for these students there was a feeling of immobility, with no clear sense of progress over time or of a destination. Both GCSE and FS were “mathematics” and “required”, with these qualities outweighing any distinctions between them. Seeing mathematics as a separate subject could explain the perception, across all qualifications, that mathematics had little relevance to students’ main vocational courses (see Figure 3). While for some students, a qualification being required was sufficient reason for them to take it, others disliked or placed a low value on mathematics as a subject and so were not interested in the mathematics journey.

I don’t think it’s helpful in a society to bring up young adults to think they can’t thrive or be successful if you don’t have a “maths brain”. I don’t think maths should be held up in higher esteem than any other subject. I think there is too much pressure on people to be clever in the “right way”. (17, GCSE)

While not a majority view, this third perspective is perhaps a reminder that the features of mathematics qualifications are not everything, and that students’ relationship with mathematics as a subject is also key.

Success and failure

Passing and failing were central to students’ experiences, both in relation to past examinations and to the consequences of success or failure in their current qualifications.

I failed it twice before and I want to pass it. (Male, 17, GCSE)

I’m scared if I fail it I will be stuck on the same qualification. (Male, 17, FS L1)

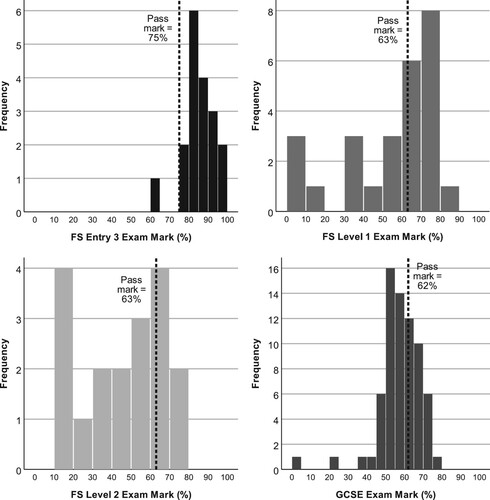
As already seen in Table 2, there is some support for the linear view of qualifications from students’ examination results since pass rates decrease dramatically with the difficulty of the qualification. However, it also appears that progression through the levels does not happen at a consistent rate, so that it becomes harder to progress the further on you get. The pass rates for FS level 2 and GCSE were very similar, which perhaps supports rather the divergent view of these two qualifications as equally difficult alternatives. In contrast, the much lower GCSE pass rate (and higher FS level 2 pass rate) in the national data is perhaps an indication of how different college policies about who takes which qualification can impact on students’ opportunity to succeed. Of the whole sample (N = 133), less than one in five students (17%) reached the finish line by achieving GCSE grade 4 or above and so would have no further requirement to study mathematics. A further 29% of students passed their current level so would progress to the next level in the following academic year, while the majority (55%) would remain on their current level and effectively repeat the year, as far as their mathematics qualification is concerned.

In addition to the level of difficulty, the number and type of examinations also have an impact on students’ success, for example “FS can be retaken whereas GCSE you only have one try” (Female, 18, FS L1). FS have on-demand assessments which students can re-take multiple times within the same academic year, whereas GCSE has a maximum of two attempts. This affects the mark distributions, shown in Figure 4, and in particular the distribution on either side of the pass mark of students who scored close to this boundary. For all levels of FS, more students narrowly passed than narrowly failed, whereas the opposite is true for GCSE. Hence it appears that having additional opportunities to take the exam enables a greater proportion of FS students to get across the line by achieving the pass mark at least once.

Figure 4. Examination mark distributions for FS and GCSE qualifications.

What matters in a mathematics qualification?

Having considered the relationship between FS and GCSE, this section looks at three aspects of these qualifications which were important to students: alignment of purpose, opportunity to achieve, and familiarity.

As already seen, students assigned a range of purposes to mathematics qualifications, whether learning useful skills, gaining a respected qualification, or being allowed to stop studying mathematics. However, where these purposes did not align with students’ own goals this led to frustration and sometimes a desire to opt out completely.

I feel like maths is unnecessary as we don’t need much more than to know how to add, take away, subtract and divide as that’s used in everyday life, but we are forced to learn things that are irrelevant … I’m wasting my time learning something I don’t need in life. (Female, 17, GCSE)

I hate having multiple lessons I'd rather focus on one main [vocational] course. (Male, 17, GCSE)

Alignment of purpose is certainly a major factor in the popularity of GCSE over FS (see Figure 2), since the function of GCSE as both a gatekeeper and exit qualification aligned with many students’ aspirations.

I want to get my GCSE maths qualification to get on level 3 on my main course. (Female, 18, FS E3)

The university application on a nursing degree requires at least a 4 and I’d need to do a year of science which requires a 4 also for me to attend. (Female, 18, GCSE)

I want to get it over and done with! (Female, 17, GCSE)

A second consideration is the opportunity to achieve something of value that is “doable but challenging” (Male, 16, GCSE). Hence courses that were too easy were seen as not worthwhile and one student questioned whether a single diagnostic test was sufficient to set the right level of challenge for the year:

It’s proven I found Entry 3 really easy. I don’t think a small maths test at the start of college is fair enough to judge what class people should be in. (Male, 17, FS E3)

Many students wanted the opportunity to understand mathematics better, as well as the satisfaction of being able to improve on a previous grade.

To prove to myself that I can pass maths and prove to my family I can. (Male, 16, FS L1)

A third, rather unexpected, theme was the value of familiarity. Students appreciated having time to become comfortable with the way a qualification works, including not only content but also the modes of assessment. Having been used to GCSE at secondary school, some FS students would have preferred the chance to retake the same course rather than being moved on to something different.

I just came out of doing my GCSE so I think it would be fair to redo and learn more GCSE questions. (Female, 16, FS E3)

I have been learning GCSE maths since year 10 [age 14] and I have gotten used to the way and layout of GCSE. (Female, 17, GCSE)

Discussion

This study aimed to answer three questions: (1) How do vocational students understand the relationship between GCSE and FS? (2) How do students’ experiences of success and failure in mathematics relate to these understandings? (3) What do students value in post-16 mathematics qualifications? Regarding the first question, there is evidence for three distinct perspectives of post-16 qualifications, described here as a race, as a fork in the road, and as a non-journey. Each of these perspectives has consequences for the kinds of issues that students experience in navigating the post-16 mathematics “journey”, including how they view success and failure, and which values are prioritised. All three research questions will therefore be discussed in light of each of these metaphors.

Firstly, the linear perspective reflects the policy language of FS as a “stepping stone” to GCSE but with the additional elements of time pressure and a fixed end point, making it more like a race. For students taking this perspective, the key value is having the opportunity to succeed through being on the right level of course, with those on the lower levels potentially feeling that they are prevented from moving on and having the chance to reach the finish line. This mirrors the findings of Boaler, Wiliam, and Brown (2000) around ability grouping in schools, where placing students on the foundation tier not only restricted their access to curriculum but, at that time, also denied them the opportunity to gain the crucial GCSE grade C, resulting in disaffection and demotivation. In the same way, students entered for FS at college may be demotivated by not having the opportunity to improve their GCSE grade. Cornish (2017) describes similar FE policies as exclusionary, citing cases where only having access to low level mathematics qualifications prevented students from progressing to higher-level vocational courses. Likewise, Dalby and Noyes (2018) assert that “the numbers taking high-level qualifications are restricted, not by the students’ abilities, but by college policies that are highly influenced by financial and performance concerns” (p. 574). There is therefore a need to reconsider how these financial and performance levers can be used to expand rather than restrict students’ access to higher-level mathematics.

Within this perspective, examination success is crucial to being able to progress towards the finish line of achieving a GCSE grade 4, but students’ chances of success appear to be affected by differences in how FS and GCSE assessments are conducted. Students are aware of some of these differences, such as the greater number of retakes allowed for FS. However, there are also hidden differences. For example, FS assessments have a fixed pass mark with no limits on how many students can pass, whereas GCSE grade boundaries are set using “statistical predictions” to ensure consistent levels of difficulty from year to year, resulting in approximately 37% of candidates being awarded a grade 3 or below (Ofqual, 2014). It could therefore be said that some thresholds are more “magical” than others, since not all post-16 qualifications provide students with an equal chance to succeed. This goes beyond the single dimension of “level”, being a weighing up of risks rather than a mechanical process; the risk of failure is balanced against the risk of holding students back from progressing. As Biesta (2013) argues, “education always involves a risk” (p. 1). Notably, there is a risk involved for colleges as well as for students, since pass rates affect the college’s Ofsted grading¹, which in turn affects levels of external monitoring and access to funding. Differences in how these competing risks are assessed could explain why differences exist between college policies for placing students on post-16 courses, and further research is needed to assess whether some of these policies have more equitable outcomes than others. It also appears that students frequently have a different assessment to that of the college; in this case, almost a third of students were prepared to gamble on a higher qualification than the one they were placed on. This raises questions about how to involve students in risky decisions that directly affect their educational futures, and moreover how this flexibility can be enabled and incentivised through changes to policy levers.

The second perspective, where the relationship between GCSE and FS is seen as a fork in the road, relates to practitioners’ view of the two qualifications as “alternative routes” (ETF, 2015) but with the nuance that these routes are divergent not parallel. That is, they are mutually exclusive pathways leading to entirely different destinations, not alternative means to get to the same place. From this perspective, the risk for students is that of missing out; they can either have the benefit of the greater use value of FS or the greater exchange value of GCSE but not both. The important thing for students then is that the destination is aligned with their own purposes for studying mathematics. Indeed, the Association of Colleges has called for increased flexibility in FE funding so that students can pursue the qualification most appropriate to them (Sezen, 2019). This would also require much greater student involvement in the decision-making process, with potential benefits in increasing student autonomy, which according to the self-determination theory literature can improve motivation, independence, and even attainment (e.g. Guay, Ratelle, & Chanal, 2008; Middleton & Spanias, 1999). However, the flip side is that, where none of the available qualifications align with students’ purposes, a natural response is to opt out altogether, as in the current study where a small minority (9%) of students did not want to study any form of mathematics. Indeed, to some extent students may already make these decisions for themselves, as they always have the choice of whether to attend lessons (Head, 2016) and whether to engage in the lesson once there (Duffy & Elwood, 2013). It is therefore worth bearing in mind that for some students, neither use nor exchange value is sufficient reason to study mathematics qualifications, at least in their current forms. Success and failure in this divergent model are likewise relative. For a student whose primary purpose is the utility of mathematics, then passing an examination becomes irrelevant as long as they have gained the necessary skills. In contrast, passing is crucial for those whose objective is the exchange value of a qualification, since it is only by passing that you have something to (metaphorically) exchange.

The idea of these alternative routes as divergent rather than parallel perhaps helps to explain why it has proved so difficult in practice to implement one qualification that encompasses both use and exchange value. This goes beyond England, with many countries having to balance the competing political priorities of “either international league tables (through abstract maths) or economic development (through functional maths)” (ETF, 2014, p. 13). One suggestion mooted by employers and FE teachers in the UK is the introduction of FS level 3, although it is acknowledged that “it would only have currency if there were recognition of its value by employers” (ETF, 2015, p. 15) and, I would add, by universities. This sticking point seems hard to overcome, with the low status of FS being one of the reasons for the introduction of GCSE resits in the first place (Wolf, 2011). An alternative solution is the proposed new post-16 GCSE which aims to increase the vocational relevance of the mathematics curriculum while benefitting from the status and credibility of the “GCSE brand” (Davies, Dudciz, Lee, Newton, & Stripp, 2020). While this seems to resolve the use or exchange value dilemma, it raises questions about how the new qualification would be positioned in relation to the existing GCSE. Since they would presumably be equivalent in terms of level, there would need to be not only a re-valuing of the lower GCSE grades but also careful consideration of what counts as progress. For example, would a student who achieves grade 3 at age 16 and then grade 3 in the post-16 GCSE be considered to have made progress or not? There are parallels with the positioning of the Core Maths qualifications, which were recently introduced as an “alternative pathway” to the well-established mathematics A-level but which both students and staff frequently view in terms of a vertical, hierarchical relationship, for example, students who do not do well on the A-level course can “drop down” onto Core Maths (Mathieson, Homer, Tasara, & Banner, 2020). Hence it is not only the content and level of new qualifications that are important but also their positioning, a consideration that has relevance beyond the current context.

For a small minority, the answer to the question “How do vocational students understand the relationship between GCSE and FS?” is that they do not. In terms of the journey metaphor, this is a kind of non-journey or immobility. From this perspective, FS and GCSE are either indistinguishable or any differences between them are irrelevant, with students perhaps seeing both as shorthand for mathematics in general. This is understandable, since in their prior schooling there is likely to have only been one option. However, the small numbers taking this perspective, and indeed the small proportion of students who stated they did not want to study any form of mathematics (9%), suggests that the presence of two competing qualifications has for most students served to expand their ideas of what constitutes mathematics. For comparison, previous studies (Bellamy, 2017; Noyes & Adkins, 2016) found overwhelming opposition to compulsory mathematics in contexts where only one qualification was on offer (GCSE and A-level mathematics, respectively), meaning that the concepts of mathematics and the specific qualification may well have been conflated. Or it may simply be that students are more willing to choose mathematics when they have a clear idea of the form it will take.

Perhaps connected to this is the value of familiarity, which is less about the connection between GCSE and FS and more about the relationship of both to secondary education. While Dalby and Noyes (2020) have recognised the importance to FE teachers and managers of qualification “stability over time”, the value of stability to students has been overlooked. Looking at the secondary-to-tertiary transition in mathematics, Clark and Lovric (2009) proposed a transition model based on the anthropological concept of a rite of passage, arguing that transition takes time and involves facing the “shock of the new” (p. 763). In FE, where the focus is on relatively short, one-year courses, students are given less time to adapt to new expectations and ways of working than in other phases of education. Whereas GCSE resit students will already be familiar with the qualification, those on FS will be likely to experience the “shock of the new” not only when they first arrive at college but also as they progress through the levels of FS, each with a slightly different set of expectations. Those who move from FS level 2 back to GCSE could even encounter something akin to reverse culture shock. Hence, there is also a need for further investigation of these mathematical transitions at the school-to-FE boundary.

Conclusion

Future qualifications development and reform is inevitable, both in the UK and internationally as countries seek to equip their young people with basic mathematics skills in a changing world. Employers and higher education institutions are both to some extent end-users of this mathematics education and are rightly viewed as stakeholders both in the implementation of current qualifications and development of new ones. However, students also have their own goals and purposes for their post-16 mathematics education. In the inflexible English system, there is currently little scope for students to influence their own directions. However, this research provides encouragement that many students would engage thoughtfully and positively, were such opportunities made available to them. If greater flexibility is to happen in practice, there must be a deliberate shift in the funding and inspection mechanisms used to direct what happens in FE colleges.

Students’ understandings of GCSE and Functional Skills qualifications go beyond the metaphors used in policy documents and thereby expose some of the unintended consequences of those policies. The metaphor of “alternative routes” is translated by students into mutually exclusive pathways in which you are required to miss out on either the use or the exchange value of mathematics. Likewise, the “stepping stones” metaphor, conjuring up images of pleasant strolls by woodland streams, is instead interpreted as a gruelling race to a far-off finish line. While the qualities of opportunity to succeed, alignment of purpose, and familiarity are all important to students, perhaps even more crucial is the positioning of new qualifications in relation to those that come before, after, and alongside.

Acknowledgements

I am very grateful to the teachers who allowed me into their mathematics lessons and the students who willingly cooperated in the study, as well as to the college for their support of this project.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Notes

1 The Office for Standards in Education, Children’s Services and Skills (Ofsted) is the UK government department responsible for inspecting educational institutions. Ofsted awards grades to institutions from 1 (outstanding) to 4 (inadequate).