Fostering a Student’s Abstraction of the Relationship Between Parallelogram and Trapezoid Within Quadrilateral Hierarchy

ABSTRACT

This article provides an analysis of a data set coming from a two-phase qualitative study that focused on fostering primary students’ abstraction of interrelations among quadrilaterals (squares, rectangles, parallelograms, rhombuses, trapezoids). The pilot study consisted of work with eight primary students operating at van Hiele level 2 (e.g., understanding quadrilaterals without interrelations). We benefitted from the teaching experiment methodology to develop a task sequence applied in a dynamic geometry environment and a paper-pencil environment to help each participant develop quadrilateral hierarchy at van Hiele level 3 (e.g., understanding quadrilaterals with their interrelations). The main study used a case study approach to investigate two primary students’ progress (Efe and Ayla, age 10). After the pre-interviews, each participant was taught the developed task sequence individually during seven up-to-one-hour teaching sessions, followed by a post-interview. This article only details Efe’s case as he worked on developing the relationship between parallelogram and trapezoid. We analyzed Efe’s data (from the pre-interview, Teaching Session-7, and the post-interview) to describe how the different parts of the task sequence fostered his abstraction of the interrelation between parallelogram and trapezoid as he moved from van Hiele Level 2 to 3. This article provides initial evidence for the classification process.

KEYWORDS:

• Interrelations of quadrilaterals
• abstraction of interrelations
• dynamic geometry environments
• affordance-constraint dichotomy
• van Hiele levels
• independent Scholar

Quadrilaterals and their interrelations are an essential part of primary school mathematics curricula. From early primary grades, students should describe and classify two-dimensional objects and understand their interrelationships (e.g., National Council of Teachers of Mathematics, 2010; Turkish Ministry of National Education, 2018; UK Department for Education, 2013). Such understanding is vital as it is transferable to different mathematical areas like measurement (e.g., Craine & Rubenstein, 1993) in later stages of schooling. For example, a student conceptualizing parallelogram as a particular type of trapezoid¹ (because it has a subset of geometric properties of the trapezoid) can also understand that the trapezoid area formula should work for finding parallelogram area. However, current practice in schools and textbooks encourages learners to treat quadrilaterals as images with a collection of disconnected definitions (Cannizzaro & Menghini, 2006; Edwards & Harper, 2010; Öztoprakçı, 2014). Our experience also suggests that students are often encouraged to memorize the relationships among quadrilaterals (e.g., a square is a rectangle). The research in this area falls short of providing ways to change such practices and curriculum design efforts. Therefore, this article details how a task sequence promotes a primary student’s understanding of interrelations among quadrilaterals in a dynamic geometry environment (DGE), the Geometer’s Sketchpad (GSP), with support from a paper-pencil environment. The research question we pursued in this case study is: How does a carefully designed task sequence foster a student’s abstraction of the interrelations of parallelograms and trapezoids as he engages in that sequence within DGE and paper-pencil environments?

Quadrilateral hierarchy is a difficult-to-grasp area. Students stay at van Hiele Level 2 (knowing shapes with certain properties without establishing any relations to other shapes) even at the secondary school level (Senk, 1989). The researchers who have worked in this area (e.g., Erez & Yerushalmy, 2006; Fujita & Jones, 2007; Molitoris Miller, 2013) give us clues about understanding quadrilaterals. An effective way to foster students’ understanding of quadrilaterals is to provide them with opportunities to develop the hierarchical structure of quadrilaterals (Craine & Rubenstein, 1993; Davison, 2003; De Villiers, 1994; Fujita & Jones, 2007). The use of DGE may positively affect students’ understanding of quadrilateral hierarchy (e.g., Lai & White, 2012). It may also help students focus on the properties of figures, think deductively, and develop better models for quadrilaterals (Erez & Yerushalmy, 2006; Jones, 2000). For understanding inclusion, Markman (1989, p. 140) highlighted the criticality of understanding asymmetry² and transitivity³ of the relations among quadrilaterals. Molitoris Miller (2013) also pointed to the importance of noticing “inherent attributes common to both the subset and superset in a hierarchical relationship” (p.273). This study details how a single student established the inclusion relation between parallelograms and trapezoids within the quadrilateral hierarchy.

Teachers have a particular role in fostering student understanding in DGE. Free experimentation with tasks given in DGE is ineffective as there is a genuine need for teacher guidance (Erez & Yerushalmy, 2006), reflection, and experimentation (Battista, 2008). DGE provides opportunities for students to explore and reflect on the (inter)relations of shape families (Hollebrands, 2007). Research (e.g., Kaur, 2015) also highlights the importance of not being limited to DGE or physical environments during teaching. Dynamic (e.g., DGE) and static (e.g., paper-pencil, manipulatives) environments should not replace but complement each other (Kokol-Voljc, 2007) as they make different contributions to students’ understanding (Komatsu & Jones, 2020) and reasoning (Zembat, 2008). Research is scarce on combining two environments (Komatsu & Jones, 2020; Maschietto & Soury Lavergne, 2013). Such investigations may give us insight into the better integration of DGE into teaching. Although we heavily used DGE, we also benefitted from paper-pencil tasks in our design.

Based on their analysis of the studies published in the International Group for the Psychology of Mathematics Education, Jones and Tzekaki (2016) highlighted the importance of systematically investigating the teaching tasks in DGE. Although we get clues from the literature about the importance of using DGE and effective instruction and teacher moves, the research is scarce in articulating appropriate curricula or tasks, especially for fostering quadrilaterals with their interrelations in geometry. For example, Komatsu and Jones (2019) focused on tasks on proofs, Forsythe (2015) investigated the use of animations to teach about the relation between kite and rhombus, Sinclair et al. (2011) examined the task development process for dilation, ratio, and proportion in GSP environment, Prusak et al. (2013) explored the promotion of area concept with specific tasks, and Trocki and Hollebrands (2018) developed a framework to evaluate the quality of tasks based on student mathematical activity in DGE. These efforts need to be supported with further research to understand better how to foster an understanding of the interrelations of quadrilaterals. Our study aims to contribute to this research area. As Komatsu and Jones (2019) did for a different purpose, we developed tasks and empirically tested them to better understand quadrilaterals’ abstraction with their interrelations. Very few research-based sources inform us about teaching and learning quadrilateral hierarchy. Next, we present three studies focusing on task sequences to teach quadrilaterals.

To help learners understand parallelograms and their interrelations with squares, rhombus, and rectangles by bypassing van Hiele Level 3 thinking, Gal and Lew (2008) designed a task sequence to improve secondary school students’ concept images of parallelograms. They used physical strips and hinges in the sequence to make dynamic parallelograms that allowed slow and continuous shape changes from a parallelogram to a square, rhombus, and rectangle. This method proved promising at the secondary school level but needs further development, especially at the primary level.

Another effort we located in the literature was about using the animation-in-demand feature in a DGE in Smart Board, “a dual delivery of geometric concepts by texts, narrations and words accompanied by pictures, illustrations and animations” (Leung, 2008, p. 1007), to teach primary students about inclusion and transitivity among quadrilaterals like square, rhombus, and parallelogram. They found this approach effective and promising; however, the particulars of the shifts in student reasoning need further clarification.

One final resource, Shape Makers⁴ (Battista, 2012), consists of computer-assisted lessons to teach students about quadrilaterals and their interrelationships. Battista (2012), in those lessons, used a representative figure for each type of quadrilateral to represent all figures of this type and called it a shape maker – for a square, it is called a square maker – and all lessons were designed to have students work on different shape makers. However, as Battista (2012) acknowledges, parts of the given tasks were hard for some students and fell short in promoting thinking about quadrilateral interrelations leading to a hierarchy.

The commonality of all this research (e.g., Battista, 2012; Gal & Lew, 2008; Leung, 2008) is that the researchers benefitted from van Hiele Theory and used dynamic contexts (i.e., movable strips with hinges, animations, DGE) to help learners develop their understanding of quadrilaterals and/or their interrelations to some extent. What is yet to be further explored at the primary level is shifts in the geometric reasoning of students and how those shifts are fostered. Our research attempts to contribute to this research genre at the primary level by analyzing what it means to foster a learner’s thinking about property-based abstractions that pave the way to hierarchical thinking and overcoming common difficulties. We revised the Shape Makers curriculum and created our design to foster an abstraction of quadrilaterals.

Conceptual Framework

In characterizing students’ levels of learning, we benefitted from several constructs and descriptions highlighted by Battista (2008) and van Hiele Theory (Pegg, 2014; Van Hiele, 1986). We used Battista’s interpretation of constructivism as an orienting framework: “mathematics learning comes about as individuals recursively cycle through phases of action (physical and mental), reflection, and abstraction in a way that enables them to develop ever more sophisticated […] reasoning” (p.136). We consider actions in this definition as students’ mental or physical acts as they engage in the given tasks. Dragging a vertex of a rectangle (physical) and comparing its opposing side lengths (mental) can be considered examples of actions. On the other hand, reflection is consciously thinking about actions, the components of those actions, and their results (Battista, 2008), as well as identifying commonalities among them (Glasersfeld, 1995). For instance, an example of reflection is deeply thinking about the connection or the difference between a quadrilateral having at least one pair of parallel sides and a quadrilateral with exactly two pairs of parallel sides. Finally, as an essential construct in constructivism, abstraction is the mechanism leading to learning and defined as understanding the logical necessity of an observed pattern (Simon et al., 2010). For example, in addition to other common properties, rectangles have the affordance of having two pairs of congruent sides (which can be observed as a pattern by a learner in a DGE), which allows one to understand why rectangles include squares (the necessity of four-congruent-sides property satisfying the property of two-pairs-of-equal-sides) – such an understanding can be considered as an abstraction.⁵

van Hiele Theory characterizes learners’ geometric thinking with different but hierarchical levels of abstraction, which is informative in investigating learners’ progress. These levels are detailed below using original and most recent literature (Battista, 2008; Pegg, 2014; Van Hiele, 1986).

Table

Level 0 (VH0)	Learners pay attention to the part of a shape’s visual characteristics but cannot identify common shapes.
Level 1 (VH1)	Learners recognize geometric figures by their appearance as visual wholes and ignore their properties. Visual perception and prototypes dominate learners’ thinking when identifying geometric figures. For these learners, for example, a rectangle is a rectangle because it looks like a window, or parallelograms are not rectangles because they are slanted.
Level 2 (VH2)	Learners identify and characterize geometric figures by their geometric properties and spatial relations between their parts. At this level, visual appearance is overshadowed by geometric properties. Students’ relational conceptualizations may range from visual informal reasoning (e.g., a square has four sides) to formal property-based reasoning (e.g., all sides and angles are equal on a square). The properties of geometric figures and the figure classes are independent. For VH2 thinkers, a square is a square because it has four equal sides and four right angles, not because it looks like a picture or is an item previously labeled as a square, as in VH1. Again, for these thinkers, a rectangle has two pairs of congruent sides with right angles, but it differs from a square.
Level 3 (VH3)	Learners understand that the properties of geometric figures are interrelated, and so are the classes of geometric figures. They can now classify figures hierarchically and justify that hierarchy. For this level thinker, a square is a rectangle because the property of ‘two pairs of congruent sides’ includes the property of ‘four congruent sides.’ Note that VH3 can be at the empirical level (e.g., empirically concluding “if a shape has one property it has another” (Battista, 2008, p. 852)), at the componential analysis level (e.g., a quadrilateral with four right angles must have equal opposite sides), at the logical inference level (e.g., mentally operating on property statements rather than images via logical inferences), or at the hierarchical classification level (e.g., justifying hierarchy through logical inferences).
Level 4 (VH4)	Learners can develop proofs using necessary and sufficient conditions and understand deduction.
Level 5 (VH5)	Learners can explore different geometries (e.g., spherical, Euclidean) and compare different deductive systems.

These components of action, reflection, and abstraction guided us in designing the tasks, as detailed in the following section. The tasks were embedded mostly in DGE and, to some extent, in a paper-pencil environment that allowed students to actively participate (a feature of constructivist theory (Erez & Yerushalmy, 2006)) and use dragging to investigate invariant relations among quadrilaterals. In making sense of participants’ developing abstractions and how they engaged in the designed activities, we used van Hiele Theory.

We benefitted from two other task design and data analysis constructs: affordances and constraints. Based on the past literature (e.g., Gibson, 1986; Greeno, 1998), Kennewell (2001) describes the affordances as “the attributes of the setting which provide the potential for action” (p.106) and the constraints as the “conditions and relationships amongst attributes which provide structure and guidance for the course of actions” (p.106). In task design and during the teaching, as part of the intervention, we tried to help participants reflect on the constraints and affordances of the properties of the quadrilaterals. For example, when comparing a trapezoid with a parallelogram, an affordance of a trapezoid is that it can have different side lengths. In contrast, a parallelogram has two pairs of equal sides, a constraint. Another example is that a parallelogram has two pairs of parallel sides, which is a constraint compared to a trapezoid because a trapezoid has at least one pair of parallel sides (an affordance of a trapezoid when compared to a parallelogram).

Finally, we used the language of shape family (Forsythe, 2015) for each type of quadrilateral during the study. For example, when a previously constructed parallelogram on a GSP screen is dragged from one of its vertices, one can get parallelograms with different sizes, shapes, and orientations but with preserved mathematical properties. We used shape family to refer to, for example, the collection of all these parallelograms.

Method

This article analyzes a partial data set from a two-phase qualitative study (the pilot and the main study phases) where each used a particular qualitative method feeding the other. We used the pilot phase, a teaching experiment, to test ideas for possible tasks to foster abstractions of quadrilateral interrelations and inform our instructional and research decisions. We then used the main study, a case study approach, to investigate the process contributing to students’ different abstractions. The details of each phase regarding participants, methods of data collection, and data analysis procedures are in subsequent sections below. Note that this article only details a single student’s work (Efe’s) from the main study.

Pilot Study Data and Analysis Procedure

Participants

We approached 12 primary school student volunteers via convenience sampling and conducted pre-interviews (see for further evidence). As a result of the pre-interviews, eight students were recruited for the pilot study, and two were recruited for the main study. The remaining two students were eliminated since they were not at the VH2 level.

Method

We benefitted from the teaching experiment methodology (Steffe & Thompson, 2000) in designing the teaching sessions to investigate how certain parts of the task design and teacher moves fostered students’ abstractions of quadrilateral interrelations. We revised certain parts of Shape Makers (Battista, 2012) as needed and piloted them on these eight VH2-level thinkers. The pilot phase took about two months in total. A detailed description of Shape Makers and our adaptation is given later in the article.

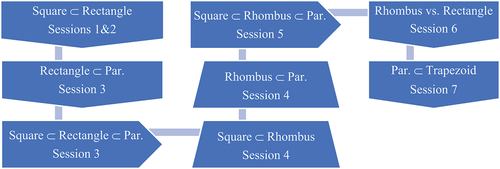
The second author was the teacher-researcher throughout. Each participant was taught individually during the pilot phase to explore their ways of operating and mathematical realities as they engaged in the tasks and “the progress students make over extended periods” (Steffe & Thompson, 2000, p. 274). After each teaching session, the teacher-researcher met the first author to debrief and analyze students’ progress through van Hiele levels and the working or problematic parts of the developing task sequence. We initially considered the Shape Makers curriculum a rough instructional model and a guide to decide on a tentative progression of tasks. We applied the developing sequence to different participants, as detailed in Table 1. After each trial, we revised and applied the sequence in the subsequent trial. Such development led us to a sequence as in Table 2. Throughout this process, the pilot sessions for each participant were used to reflect on models of students’ thinking and learning, teaching moves, and task revisions which is briefly described in Table 1. In each trial, we developed hypotheses, tested them, and revised them for task sequence revisions. Each trial informed its successor (Simon et al., 2010; Steffe & Thompson, 2000) regarding student progress and task design. We repeated these trials five times until we were convinced that the task sequence worked mostly smoothly.

Table 1. Description of the task sequence development in the pilot study.

Pilot Trials	Tasks	Brief list of our reflections during task development
Trial 1 (Applied to Participant #1–1 session only)	1. Free experiment with shape makers – The student was given some shape makers (square, rectangle, trapezoid, deltoid, rhombus, parallelogram, a generic quadrangle that allows to make isosceles trapezoid) and was asked to do free experimentation using the dragging feature.	− Deemed useful in terms of helping the student use the dragging feature and learn about how to work with DGE − No focus on properties but some discussion about what shape makers make what part of the given picture. − Decided to consider Free Experiment and Warm-up Tasks as a single task based on student feedback and our analysis − Decided to drop deltoid from the list of shape makers since it was not in the national mathematics curriculum and was going to make things even more complicated.
	2. Warm-up Task – The student was given a picture of a shape collection and asked what parts could be made with square, rectangle, rhombus, parallelogram, trapezoid, deltoid, and quadrangle that allows isosceles trapezoid.
Trial 2 (Applied to Participant #2 and Participant #3–4 sessions per participant)	1. Warm-up Task – without deltoid	− The Guess-and-check Activity allowed students to investigate shape makers and their draggable features. Therefore, we decided to drop the Game. − Guess-and-check Activity fell short of helping the student understand that a given shape maker represented the whole class of shapes it could make. We decided to expand the set of shapes and design the Grouping Activity for the next trial.
	2. Guess-and-check Activity – Students were to guess whether the given drawings could be made by each of the given shape makers. The drawings had sets of square and rectangle; square-rhombus; square-rectangle-rhombus, and square-rectangle-rhombus-parallelogram, respectively.
	3. Game – Students were given a picture consisting of different shapes and asked which of the given shape makers could make which part of the given picture.
Trial 3 (Applied to Participant #4–5 sessions in total)	1. Warm-up Task – as in Trial 1 but without deltoid	− Guess-and-check Activity now includes square-rectangle-parallelogram, square-rhombus-parallelogram − Not including angle measures and side lengths caused problems and misled students. − We decided to engage students in an investigation of shapes followed by an investigation of certain measures (e.g., interior angles, side and diagonal lengths, angle between diagonals).
	2. Guess-and-check Activity – with square-rectangle; square-rhombus; square-rectangle-parallelogram, square-rhombus-parallelogram, and square-rectangle-rhombus-parallelogram.
	3. Grouping Activity – Students were asked to group the given shapes on paper (squares, rectangles, parallelograms with different sizes, shapes, and orientations) into three groups based on the properties they have seen so far.
	4. Naming relations as child-parent-grandparent
Trial 4 (Applied to Participant #5 and Participant #6–6 sessions per participant)	1. Warm-up Task as in Trial 3	− We realized that the rectangle maker used in Battista’s design gets bigger or smaller proportionally when dragged from some vertices, which misled students. So we decided to change the construction of the rectangle maker, so the dragging gave different size rectangles. − We integrated the “checking the groups on GSP” option into the Grouping Activity, but it led students to focus on what they saw on screen rather than making a property-based analysis. We then decided to drop the GSP-checking part of this activity. − Focusing students on interrelations using the child-parent-grandparent model seemed problematic as it did not foster property-based conjecturing and argumentation. We decided to remove it and focus students on affordances-constraints of shape families from the beginning (e.g., What constraints allow a parallelogram to be limited to a rectangle? What affordances allow a rectangle to become a parallelogram?). − Including a quadrangle that allowed drawing isosceles trapezoid confused students as it required them to return to the square and build up the hierarchy again. So, we reduced the number of quadrilaterals to five (square, rectangle, rhombus, parallelogram, trapezoid)
	2. Guess-and-check Activity as in Trial 3
	3. Shape makers with measures (side lengths, interior angles, diagonal lengths, angle between diagonals)
	4. Grouping Activity on paper + allowing students to check their groups on GSP
	5. Naming relations as child-parent-grandparent
Trial 5 (Applied to Participant #7 and Participant #8–7 sessions per participant)	1. Warm-up Task – with square, rectangle, rhombus, parallelogram, and trapezoid.	− Working with affordance-constraint dichotomy worked well in establishing the hierarchy − Grouping Activity seemed to push students back to VH2 rather than operating at VH3. We decided to drop Grouping Activity. − Guess-and-check Activity now includes rectangle-rhombus, square-rectangle-rhombus-parallelogram-trapezoid and worked well. − Task 3 needs to be supported with another activity to help students reflect on some properties satisfying the others. We decided to generate riddles in addition to Task 3. − When adding trapezoid to the hierarchy directly, students had difficulty conceptualizing it in relation to other shapes. We decided to have students investigate parallelogram-trapezoid relation and then make a connection to the hierarchy.
	2. Guess-and-check Activity – with square-rectangle; square-rhombus; square-rectangle-parallelogram, square-rhombus-parallelogram, rectangle-rhombus, square-rectangle-rhombus-parallelogram-trapezoid.
	Shape makers with measures (side lengths, interior angles, diagonal lengths, angle between diagonals) as in Section 3
	3. Grouping Activity on paper only
	4. Certain Questioning – (e.g., What constraints make a rectangle a square? What affordances make a square a rectangle? Can a square be part of the rectangle family? How so?) – very close to Task 3 in Table 2

Table 2. Description of the task sequence applied in the main study.

	Warm-Up Task: Students were initially given a collection of shape makers to drag and do a free investigation. The shape makers could be dragged from at least two of its vertices in all the tasks. Then students were given the same shape makers to fit in each picture as seen on the lower part of the left column. The purpose of the Warm-up Task was to have students investigate the shape makers and see how they could be dragged from the vertices to fit into the given picture made up of a combination of square, rhombus, and trapezoid. As students did these, they started to think about the given shape makers’ operating conditions. At this stage, there was no expectation on the students’ part to generalize common characteristics or think about the properties of the given geometric figures. These initial activities were designed to serve them in learning about the use of shape makers and the main features of GSP. This part is very similar to Battista’s design.
	Task 1: Students were given a single shape maker (e.g., square maker) and a collection of figures from the same family (e.g., squares of different sizes and orientations) and from a most immediate successor family (e.g., rectangles of different sizes and orientations) and then did the following: Predicted whether the first given shape maker (e.g., square maker) could make all the given geometric figures, Checked their predictions using the given shape maker (e.g., square maker) in GSP, Investigated why the given shape maker (e.g., square maker) could (not) make figures by focusing on the affordances or constraints of the shape maker using dragging, using the teacher’s guidance, and probing. Students were then given a second shape maker from a most immediate successor family (e.g., rectangle maker) and a collection of figures from the same family (e.g., rectangles of different sizes and orientations), and the subset family (e.g., squares of varying size and orientations). Students were then asked to go through the above steps for the second family in addition to: Focusing on the relationship between the two families (e.g., squares versus rectangles) based on constraints and affordances under the teacher’s guidance and probing. (Note that when comparing parallelograms to trapezoids, students were given both shape makers together and a collection of shapes from both families. This is because by the time students developed parallelograms, they only had trapezoid left in the sequence to investigate.) Once such a process was completed, students were engaged in Task 2 before exploring an immediate successor family. The purpose of Task 1 was to have students simultaneously (and tacitly) compare one quadrilateral to its immediate successor in a hierarchy as they focused on the spatial structure of the given quadrilateral. Such operation aimed to help students consider the affordances and constraints of the given quadrilateral and its successor based on their properties. Note that the students work under teacher guidance and probing throughout their engagement with this task.
	Task 2: Students were given previously investigated shape makers (e.g., square and rectangle makers) on separate screens. By dragging and considering the measurements revealed on the screen, they were asked to investigate the given family’s properties (e.g., squares and then rectangles, respectively) regarding side lengths, interior angles, diagonals, and parallelism and to make notes of those. They went through this process for each shape maker in order (e.g., first square maker and then rectangle maker). The purpose of Task 2 was to help students investigate the geometric properties of a quadrilateral set, and its immediate successor quadrilateral set considering measurements. Note that Task 2 is not treated in isolation from Task 1. Students’ engagement with and discussions of Task 2 were constantly related to the results of students’ experiences with Task 1. In this sense, Task 1 and Task 2 went together.
What constraints make a rectangle a square? What affordances make a square a rectangle? Can a square be part of the rectangle family? How so?	Task 3: Once students had enough experience with geometric properties of the quadrilaterals (e.g., squares and rectangles) given in both Task 1 and Task 2, they were then asked to compare the properties of two sets of quadrilaterals in tandem to decide which set of properties completely include the other. The purpose of Task 3 was to enable students to complete the geometric structuring of the affordances and constraints of the given quadrilateral set compared to its predecessor set based on their properties regarding side lengths, interior angles, diagonals, and parallelism. This is the stage in which students were encouraged to heavily reflect on their experience with Task 1 and Task 2 and on the interrelations, in the absence of DGE, on paper-pencil environment.
Riddles: My opposite sides are congruent (equal), but they can all be made congruent (equal) since I am flexible. When my vertices (corners) are dragged, my diagonals always stay congruent. Who am I? Please think of all the possibilities and color the appropriate shapes that fit this description!	Closing Task: Students were given some riddles about each quadrilateral set with or without a collection of figures (e.g., the riddle on the left column is intended for the rectangles set) and asked to identify the quadrilateral set that fits the description given in the riddles on paper-pencil environment. The purpose of the Closing Activity was two-fold: (1) to help them reflect on properties of quadrilateral sets at a higher level; (2) to assess their understanding of interrelationships to see a fit with VH3. This part is also very similar to Battista’s design.

Analysis

After each pilot trial, we analyzed the student data and the working or problematic parts of the tasks for revision and enhancement. We did an ongoing analysis of that trial by focusing on the questions like the following: (1) What, in the sequence, hampers or fosters students’ van Hiele levels? (2) To what extent the student focuses on and understands the interrelations? (3) Is the student still at VH2, or is there evidence of the student’s progress toward VH3? (4) How do the different tasks involved in the design contribute to the student’s progress from VH2 to VH3? (5) To what extent does the teacher lead the student or probe his thinking about the interrelations? (6) What teaching moves impact student development positively or negatively? (7) What modifications are needed to address problems? (8) What specific language did promote student thinking about the interrelationships among given quadrilaterals? Attending to such questions was vital since they helped us focus on the shifts in participants’ ways of operating for the geometric shapes under investigation and how task design features contributed to them. For example, in answering this last question, we compared the data revealing student reasoning when the language of “child, parent, grandparent” was used to describe the hierarchy among different quadrilaterals to the data showing student reasoning when the language of “square family is part of rectangle family” was used. Such a focus, for example, also helped us better understand the conditions (e.g., use of different language) under which each designed task fostered or hampered the participants’ development of quadrilaterals and interrelations. Such experiences guided us about the terminology we adopted during the teaching. Therefore, we used shape families (Forsythe, 2015) for each type of quadrilateral.

Main Study Data and Analysis Procedure

Participants

The main study participants were fourth graders transitioning to grade 5 in two schools; one boy (Efe, age 10) and one girl (Ayla, age 10), who did not go through the pilot study. They were average students in their classes who could express themselves well and liked to experiment with and learn new mathematical ideas. The names used in this paper are all pseudonyms.

Method

The pre-interviews (conducted one week before the teaching started) with the participants showed that they were operating at VH2 for quadrilaterals most of the time, had the basic knowledge of the names and shapes of targeted quadrilaterals (square, rectangle, parallelogram, rhombus, and trapezoid) and their most fundamental properties. Once the teaching sessions were completed, we also applied post-interviews (applied during the first week following the ending of teaching sessions – see for further evidence). The teaching sessions were 2–3 days apart from each other. The main study phase, including the interviews, took one month.

The second author used the piloted and close-to-final version of the task design (see Table 2) with these two participants. There was a total of seven up-to-one-hour-long sessions with each participant. Each student was taught individually to concentrate on their developing ideas just like other researchers did to develop different concepts (e.g., Engelhardt et al., 2004; Simon et al., 2010). A teaching session still fed its successor regarding students’ needs and developing ideas, but the task design needed minor modifications. The second author videotaped all interviews and teaching sessions and used screen capturing software, Freez Screen Video Capture (SmallVideoSoft, 2015), to record the participants’ works for ongoing and retrospective analyses. Once the sessions in the main study were completed, we analyzed the data retrospectively. We developed ways to articulate the participants’ development of inclusive relations and parts of the task design, as further described below. Pre-and post-interview analyses supported these efforts.

Analysis

Upon completion of the interview and teaching session video transcription process, we viewed them all together, took analytical notes (Cobb & Gravemeijer, 2008), and wrote memos (Corbin & Strauss, 2015) about our conjectures for main-study participants’ emerging abstractions and how those abstractions fit a van Hiele level. We then started analyzing the participants’ available and developing abstractions within or in between different van Hiele levels and the task features that seemed to foster those abstractions.

This article only details Efe’s case as he worked on developing the relationship between parallelograms and trapezoids. In explaining this case, we referred to Efe’s pre-interview data, the data from teaching session seven, and the post-interview data. Since we focused on how the tasks fostered an understanding of interrelationships and their application rather than the detailed learning trajectory, we share only one student’s case here. Similar data is also available for the second participant, Ayla, which does not fundamentally differ from Efe’s data. The task sequence worked similarly for both participants; however, their speeds for completing different tasks varied because of the variations in their prior knowledge. We also focus on one participant here because of space limitations. What follows details how we analyzed Efe’s case (like Ayla’s).

Our analysis focused on Efe’s developing understanding of shape families and their interrelations as he engaged in the task sequence (see Table 2). We aimed to provide an “in-depth description and analysis of a bounded system” (Merriam, 2015, p. 37), a typical VH2 level thinker, a fifth grader. As part of the case study approach, we used multiple sources of information (Merriam, 2015) for our analysis; the video recordings of the teaching sessions, transcriptions of these sessions, artifacts revealing the student’s computer work, and our observational notes. Our purpose was to build a characterization of the student’s progressing learning based on the data chunks we identified from these sources. During our analysis, we first identified data chunks where Efe engaged in the applied tasks that seemed to impact his thinking about the geometric figures and their properties. Each data chunk had a starting and an ending point. We considered the starting point as the moment when the evidence suggested that the student did not understand the common property that led to a targeted hierarchical relationship for two quadrilaterals under investigation. We considered the ending point when we had compelling evidence for Efe’s understanding of that property. This paper only provides analyses of chunks from Teaching Session 7, which is supported by Efe’s pre- and post-interview data.

These data chunks were either stand-alone chunks where we observed progress in Efe’s understanding or a combination of segments where we traced Efe’s development when individual data chunks showed us very little (conceptual) progress on the student’s part. In either case, we considered individual or several chunks at a time to build a characterization of the students’ shift from one van Hiele level to another. In so doing, we focused on changes in Efe’s use of language (e.g., both lines move vs. lines stay parallel), whether he commented after dragging given computer constructions or without any dragging, focused on the dragging he used (e.g., starting from a particular vertex or try different corners arbitrarily), and whether his focus was on the property or the dragging and its results appearing on the computer screen.

We also looked for evidence in those data chunks of whether the student identified commonality in his experiences or just noted empirical results from using dragging. By going through several analysis cycles for each data chunk or collection of data chunks, we characterized Efe’s changing thinking process concerning the properties he focused on, how one property implies the other, and how one shape family includes the other. We also checked whether a certain part of the given task (e.g., certain questions, dragging activities, guessing) contributed to Efe’s thinking about the shape families and associated inclusion relations. If the student’s language included property-based characterization of the given shape family and its inclusiveness and was stripped from individual dragging activities or examples, we considered his understanding to indicate VH3-level thinking. When the student considered properties of the shape families in isolation without focusing on whether one satisfied the other, we considered his thinking as operating at VH2.

The Task Sequences and Their Development for Pilot and Main Studies

Battista (2012) developed Shape Makers as an add-on to the Geometer’s Sketchpad (Jackiw, 1995). This microworld provides students with shape-making objects, and students are allowed to manipulate these objects. Students can transform these shape makers by changing their sizes and orientations using the dragging feature while keeping their most essential characteristics. For example, a square maker is a ready-made square that can be dragged from some vertices by preserving its squareness. Lopez-Real and Leung (2006) named this a “drag-to-fit” strategy and considered it a conceptual tool used in DGE.

We benefitted from the idea of Shape Makers in developing our tasks. We revised it by engaging in a continuous thought experiment and testing parts during the pilot study, as mentioned before and detailed in Table 1. The pilot study allowed us to make necessary revisions to the tasks and better understand how to foster students’ understanding from VH2 to VH3 using those tasks.

We had our close-to-final version of the task sequence at the end of the pilot study (Gürhan, 2015), and we used that version in the main study. Apart from the Warm-up activity for entry and Riddles for closure, we had three main tasks specific to each shape family that allowed students to work on geometric shapes, their properties, and interrelationships, as detailed in Table 2. We consider “task” as what the students are asked to do and “activity” as working on a task influencing the resulting learning (Christiansen & Walther, 1986).

As mentioned previously, during the implementation of Shape Makers, Battista pointed out the difficulty of fostering students’ understanding of the interrelations between quadrilaterals (VH3) when students already understand those quadrilaterals as disconnected (VH2). Therefore, we revised the Shape Makers curriculum as in Table 2 to help Efe understand those interrelations and operate with them more effectively. In developing our tasks, we ran into particular problems, but attending to these problems helped us facilitate his abstractions of these interrelations, as explained below.

The overall strategy used in the Shape Makers curriculum is that students are given different shape makers (e.g., square maker, rectangle maker, parallelogram maker, etc.) mostly all at once and asked to investigate which of the presented collection of shapes (e.g., square, rectangle, parallelogram, etc.) can be made with those shape makers. For example, in one of the earlier activities, “Student Sheet 7” (Battista, 2012, p. 159), students are given all shape makers (square, rectangle parallelogram, rhombus, trapezoid, kite, quadrilateral) with name tags replaced with letters and asked to investigate their properties and identify the correct shape maker names out of that investigation. In our pilot work, we realized that having all shapes and shape makers on the screen distracted the students and did not effectively support their understanding of the quadrilateral interrelations. We also realized that establishing interrelations was beyond physical experience with all quadrilaterals simultaneously (as was the case for Shape Makers).

In contrast to Shape Makers, we first focused the student’s attention on the quadrilateral pairs and their interrelations and then slowly expanded that list of inclusions. For example, we first had the student investigate square-rectangle pairs using all the tasks highlighted in Table 2 to help him learn about their most salient properties and (asymmetric) relationships to each other. We then moved on to having the student analyze the rectangle-parallelogram pair, go through the same cycle of tasks (as in Table 2) with this pair, and finally establish inclusion relations for square, rectangle, and parallelogram (using transitivity of relations). We followed the same pattern for other quadrilaterals, as in Figure 1. Note that Efe did the same tasks summarized in Table 2 for each cycle (except for the Warm-up Activity used at the beginning only).

Figure 1. The sequence in which the quadrilaterals were investigated (“Par.” means Parallelogram).

Another critical point we considered while designing the tasks was dealing with inclusion relations. Contrary to Shape Makers, while handling a quadrilateral set, we had Efe focus on the constraints and affordances and compare it with the successor quadrilateral set in the background. For example, in the context of square and rectangle (successor), although the task seemingly targeted examining only the square, the shape set on the screen consisted of squares and rectangles (e.g., Task 1 of Table 2). In addition, we asked why the square maker could not make other shapes and under what conditions it could make them both during the use of GSP and the reflection part in a paper-pencil environment. Therefore, the student had the chance to focus on the constraints of the square with “why can’t the square make it?” and focus on the affordances of the rectangle with “under what conditions (affordances) could it make it?” Such a design feature was intended to encourage the student to focus on the asymmetry relations between targeted quadrilateral sets. At this point, he was allowed to move to a successor set, rectangles, and compare the geometric properties of the rectangle with those of the square, even if that was not mentioned explicitly in the task. Although the given shapes on the screen were squares and rectangles, they intended to direct the student’s attention to the rectangles because he only worked with the rectangle maker. At this stage, he was given a chance to pay attention to the affordances of the rectangles with the question, “Why is it that the rectangle can produce all shapes?” and to the constraints of the squares by asking, “How can one constrain the rectangle so that it can produce the square?” (asymmetry of relations).

We also paid particular attention to the student’s investigation of the properties of quadrilaterals in detail (Task 2). This phase, in which the student examined the quadrilaterals regarding side lengths, angles, parallelism, and diagonal properties, allowed him to collect and interpret data about quadrilateral sets. We focused on these four properties and measures as these properties are representative and sufficient to investigate the quadrilateral sets’ spatial essence (Battista, 2008). Such focus also allowed the student to determine what properties were invariant in compared quadrilaterals. Table 3 summarizes the difference between our design and Shape Makers.

Table 3. Difference between Shape Makers and our task design.

Shape Makers	Our Design
The activities use all shape makers at once to investigate the properties of all shapes: “Which Shape Maker can make the least number of different types of shapes?” (Battista, 2012, p. 153)	The activities involve shape-family pairs or triplets sequentially rather than all at once (using a bottom-up approach to help them think about asymmetry and transitivity relations).
The focus is on properties in the following sense: 1. Can every shape made by the Square Maker also be made by the Rectangle maker? Explain why. 2. Can every shape made by the Rectangle Maker also be made by the Square Maker? Explain why. 3. Why can the Rectangle Maker be used to make squares? 4. What property or rule could be added to the Parallelogram Maker to make it a Rectangle Maker? (Battista, 2012, pp. 189–190)	Focusing on inclusion relations using affordance-constraint dichotomy for each shape-family pair and allowing students to think about shape families with the affordances and the constraints of their properties: “What affordance does the parallelogram family have that the rectangle family does not?”
Using language such as “every rectangle is also a parallelogram” or “every parallelogram is also a rectangle” (Battista, 2012, p. 193)	Using language such as “rectangle family is part of parallelogram family” or “parallelogram family includes rectangle family.”
Mixing spatial features and measurement Rectangle makers proportionally gets bigger/smaller from certain vertices in GSP	Moving from investigations with spatial features to measurement No proportional expansion of shape makers.

After this examination in DGE, the student was asked to compare quadrilateral sets based on geometric properties in a paper-pencil environment, which encouraged further reflection. While making this comparison, the student was encouraged to consider that the relevant feature of one quadrilateral type (e.g., all the sides of the square are equal) guarantees that of the other type (e.g., the opposite sides of the rectangle are equal) for the geometric properties he distinguished between the two sets (e.g., the side length property for squares and rectangles). The following section details how such an approach allowed Efe to make sense of inclusion relations.

Results

We share Efe’s development of the trapezoid and its relation to the parallelogram only in this section. We aim to analyze how the kind of abstraction each task fostered in investigating the inclusion relations between parallelogram and trapezoid. The data presented here comes from Session 7 of the main study and the interviews. Such limited focus is because the trapezoid was the most advanced quadrilateral used in the design. Our purpose in this paper is not to provide a complete learning trajectory for the entire quadrilateral hierarchy but to give evidence for how the tasks fostered abstractions. As uncovered in the pre-interview, Efe’s initial understanding is summarized next.

Summary of Efe’s Understanding as Revealed in Pre-Interviews

Efe considered square as follows: “its basic properties are, it has four corners, four sides […] all side lengths are equal, […] all angles are equal, 90 degrees.” He could label squares, differing in size and orientation, as squares, showing a VH2 level thinking. He considered a rectangle a figure with a “pair of opposite sides congruent; all angles 90 degrees just like a square.” Efe considered squares different from rectangles and rectangles different from parallelograms (“no because all angles of a rectangle are 90 degrees”), suggesting non-VH3 level thinking. For Efe, the parallelogram was a figure having “opposite sides parallel […] has four corners, […] angles are not equal.”

In contrast, a trapezoid was a figure with “four sides that are different […] that cannot be the same.” When it comes to the rhombus, Efe thought about it as “it looks more like square, its interior angles are not equal, it is a little more slanted than square, […] its opposite sides are equal.” He distinguished the rhombus from rectangle because “angles of a rhombus are not 90 degrees.” Rhombus was also different from trapezoid for Efe because “only opposite sides of a rhombus are equal, all sides are not different in length.” Finally, when questioned, he also considered square and trapezoid different since “all sides of the square are equal, and all interior angles are 90, but it is not like that in trapezoid, its sides are not equal.”

These initial understandings suggest that Efe could identify the salient geometric properties of quadrilaterals above in isolation without identifying interrelations or any hierarchy. In this sense, he was not operating at the VH3 level but carried the main characteristics of VH2 for the given quadrilaterals. However, his understanding of the trapezoid was quite limited.

Comparing Parallelogram and Trapezoid

The data chunk in Figure 2 concerns Efe’s establishment of the relationship between parallelogram and trapezoid. Before entering this dialogue, Efe could talk about the square, rectangle, parallelogram, and rhombus with their salient properties.

Figure 2. The relation between parallelogram and trapezoid – Data Chunk 1 (Task 1 – Time: 00:00–03:10 minutes).

Abstractions Fostered During Efe’s Engagement in TASK 1

Before Session 7, Efe worked on parallelograms and developed a square, rhombus, rectangle, and parallelogram hierarchy. Therefore, the teacher-student interaction illustrated in Figure 2 is about a comparison of parallelograms and trapezoids all on one screen. Upon entering Session 7, Efe understood parallelograms and trapezoids at VH2, though his understanding of trapezoids was limited, mainly at the empirical level. He could think of a parallelogram as a quadrilateral with two pairs of parallel and congruent sides and consider a trapezoid with a single pair of parallel but non-congruent sides (a limited view; visual-informal reasoning). In addition, he could talk about these families without being dependent on any specific images.

Efe was given the task (with a computer screen as in Figure 2) and asked to judge the given quadrilaterals by looking at the screen without using any feature of GSP (e.g., dragging, measuring) first. His initial reaction was to identify the shapes #2, #3, #4, and #6 as parallelograms (Line #2), perhaps by operating with his current understanding of parallelograms at VH2. However, when questioned about the other shapes on the screen, he separated them from the parallelogram family and labeled trapezoids “oblique shapes” (Line #4) as an exclusive family. His judgment was based on the visual, holistic, spatial features (“oblique”) of the given trapezoids rather than their geometric properties using formal property-based reasoning. In this sense, Efe initially considered parallelograms and trapezoids disconnected at VH2 as his comparison was based on the visual and spatial aspects rather than the geometric properties of the parallelograms or the trapezoids when comparing both sets of shapes (Lines #1–4).

When probed about the parallelogram’s constraints (Lines #5), Efe focused on both quadrilaterals’ geometric properties but isolated one shape family from the other. He considered parallelograms as having “opposite equal sides” (Line #6) whereas trapezoids as having “no equal sides” (Line #6) and considered the shapes #1, #5, #7, and #8 with different orientations as trapezoids. His treatment of trapezoids suggests that he operated from the spatial features of trapezoids apparent on the screen (visual informal reasoning). At this point, for Efe, the trapezoid was an “oblique shape” with “all sides unequal” (Line #10) and was not related to a parallelogram – an example of understanding at VH2. For Efe, the given trapezoid images on the screen (excluding parallelograms initially) could be considered a set of trapezoids without any affordances. They were, in a sense, rigid quadrilaterals having oblique and unequal sides – a limited, visual, holistic understanding of the trapezoid family, which we labeled as Abstraction #1 (A#1-VH2).

In the “checking” part of the activity, when allowed to drag the given trapezoid maker to check whether it could make parallelograms (Line #11), Efe dragged the corners of the trapezoid maker and fitted it on Shape #2. Without checking other shapes, he suddenly mentioned that “It can draw all the shapes” (Line #13), which suggests a shift in his thinking. Note that he dragged the trapezoid maker over to Shape #2 only and did not need to empirically check whether it fitted on the others (Line #13). This suggests that he thought about parallelograms as a whole family; in other words, for Efe, if a quadrilateral maker could make one member of a family (a parallelogram in this case), it could make all members in the family (all parallelograms in this case). However, such a shift seemed to depend on visual cues from the drag-to-fit strategy. Initially, he was operating from the visual-spatial features of trapezoids (A#1-VH2 as in Lines #1–10) and considering the sets of parallelograms and trapezoids disconnected, whereas he now suggested that all the given shapes could be regarded as trapezoids (Lines #11–13). He now considered the trapezoid a quadrilateral with more affordances than a parallelogram, indicating formal property-based reasoning at VH2. However, this needed to be further reflected upon and clarified.

The teacher then probed Efe by asking about the constraints of a trapezoid (Lines #14, #16) and affordances that would allow a parallelogram to make a trapezoid (Line #18). In both cases, Efe was able to identify changing angles and sides without any limitation (“can change … as we wish;” Line #15) as the affordances of trapezoids and consider the same properties as constraints of the parallelograms (“needed to change its sides and its angles,” Line #19). Hence, the properties of changing sides and angles without limitation served Efe as an affordance for trapezoids and simultaneously a constraint for parallelograms.

For Efe, the trapezoid now was a quadrilateral with affordances of changing sides and angles that could also include parallelograms because the affordances of the trapezoid maker (e.g., changing side lengths, changing angles) allowed it to make all the images (including parallelograms) on the screen – an example of formal property-based reasoning at VH2. We called this Abstraction #2 (A#2-VH2). This way of thinking might seem like a VH3 level thinking since Efe now considered trapezoids inclusive of parallelograms. However, trapezoids were more visually flexible and draggable quadrilaterals for Efe. He benefited from the affordances provided by the drag-to-fit strategy. He thought holistically about the images of trapezoids and parallelograms without paying much attention to the interrelationships among the geometric properties, so he lacked VH3-level thinking. We believe this is because of the limitation that Task 1 imposed on the student’s activity. The shift to A#2-VH2 was because “dragging,” and “fitting” were the main activities imposed by Task 1 as planned.

So far, the teacher supported Efe’s activity by asking him about the constraints of parallelogram and trapezoid and focusing on what shapes a quadrilateral maker could make and why it could not make other shapes. These questions were part of Task 1, which with access to the dragging feature of GSP, collectively allowed Efe to move from A#1-VH2 to A#2-VH2, as detailed above. However, such a shift was fragile and bounded by visual clues as it was limited to a drag-to-fit strategy.

Abstractions Fostered During Efe’s Engagement in TASK 2

Before Data Chunk 2, Efe investigated some geometric properties of trapezoids regarding diagonal lengths and angles between diagonals. Based on dragging and observing the given measures, Efe realized that diagonal lengths and angles between diagonals operate just as in a parallelogram. With such additional features, he moved into Data Chunk 2, presented in Figure 3.

Figure 3. Zooming in on the geometric properties – Data Chunk 2 (Task 2 – Time: 08:30–9:35 minutes).

Efe started Task 2 with A#2-VH2. In other words, he understood the trapezoid as a shape having the affordances of changing sides and angles. However, this understanding was developed due to engaging in Task 1 through dragging and reflection without actual measures. On the other hand, Task 2 and the teacher’s probing/leading brought in angle measures, side lengths, and parallelism on the table. As seen in Dialogue 2, his initial reaction to the question about the parallelism of one of the pairs of sides on the given screen was, “No, they are not parallel” (Line #2). However, he realized that parallelism was possible once he was allowed to drag the unparallel pair of sides (Lines #8–10). Therefore, there was a shift from “no parallelism” (Lines #2–6) to “possibility of parallelism” (Lines #7–10) for the second pair of sides when vertices were dragged. He also knew that one pair of sides must be parallel (“they are always parallel” – Line #12), whereas the parallelism for the other set is dependent on dragging (“but AD and BC are not always parallel” - Line #12). Efe’s interaction with the dragging tool and probing of the teacher allowed him to expand his understanding to a form that included parallelism property for trapezoids. For Efe, a trapezoid now had at least one pair of parallel sides (Line #8, Line #12) and affordances of changing sides and angles, including the changing angle between diagonals. We labeled this understanding as Abstraction #3 (A#3-VH2), which in a sense, was an expansion of A#2-VH2 and reflected formal property-based reasoning. Lines #15–16 of Dialogue 2 can suggest to the reader that the teacher was leading Efe because the teacher was verbalizing the conclusion and Efe only approved it by saying “yes.” From Efe’s post-interview data (Data Chunk 5), we will later see that this is his real understanding, not depending on that probing/leading.

Task 1 encouraged Efe to use the drag-to-fit strategy to focus on spatial aspects of given shapes with limited abstractions (A#1-VH2 and A#2-VH2). In contrast, Task 2, with dragging and teacher probing, allowed him to zoom in on the geometric properties of the trapezoid and expand his understanding of the trapezoid to include parallelism (A#3-VH2). However, all this depended on heavy use of dragging and teacher probing/leading, and it was all limited to a trapezoid context only.

Even though he made some progress, Efe operated at VH2 primarily from formal property-based reasoning. In other words, the participant still needed to establish the interrelation between trapezoid and parallelogram based on parallelism property. There was an upcoming opportunity to engage in deep property-based analysis, including parallelism, in Task 3, as detailed next.

Abstractions Fostered During Efe’s Engagement in TASK3

Even though Efe had property-based reasoning about trapezoid at VH2, this primarily depended on the work with the software’s dragging tool. His abstraction of trapezoid consisted of a quadrilateral with changing interior angle measures (including the angle between diagonals) and side lengths and having at least one pair of parallel sides. Although there were occasional talks about how these properties played out in other quadrilaterals (e.g., parallelogram), there was not a serious reflection made by Efe to fully abstract the interrelation between trapezoid and parallelogram yet. Task 3 was designed to allow for such reflection without DGE.

Right before Data Chunk 3, the researcher and Efe had the following exchange, which we consider part of Task 3 since it started cross-comparison between trapezoids and parallelograms based on their interrelations.

R: Okay then, can I say something like this for a trapezoid: a pair of sides must always be parallel for a trapezoid?

S_E: Yes.

R: How was it like for the parallelogram?

S_E: The parallelogram’s all sides were parallel because they did not intersect.

R: Then, can I say that two pairs of sides must be parallel for a parallelogram?

S_E: Yes.

At this point, there was not a solid abstraction of the interrelation, for the student, between parallelograms and trapezoids yet. Moreover, the above interaction might suggest further teacher leading too. On the contrary, we believe that there was a negotiation of language here (one pair “always parallel” and the other “not always parallel” versus “a pair of sides must always be parallel” (Data Chunk 2, Line #12); “all sides were parallel” versus “two pairs of sides must be parallel” – above dialogue). Next, this analysis is further developed using the data in Figure 4.

Figure 4. Considering parallelism as an affordance – Data Chunk 3 (Task 3 – Time: 16:00–18:40 minutes).

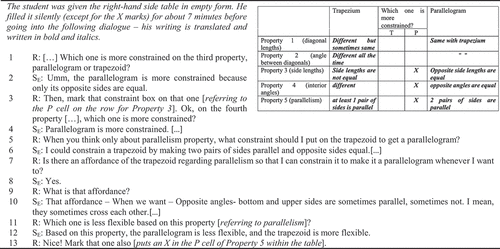
As mentioned previously, after manipulation of the given trapezoid maker in Task 2, Efe abstracted some crucial geometric properties of the trapezoid (having differing side lengths, differing interior angles, and having at least a pair of parallel sides), and he then shared them using the table given in Figure 4. At this point, he was to compare his developing understanding of a trapezoid with that of a parallelogram. The purpose was to foster property-based reasoning regarding the inclusiveness of trapezoid on Efe’s part. Upon completing the table silently, the dialog in Data Chunk 3 continued analyzing the geometric properties of both trapezoids and parallelograms. His written and follow-up verbal responses (as in Lines #1–4) suggested he abstracted that having congruent-opposite sides and congruent-opposite interior angles were constraints for a parallelogram when compared to a trapezoid. In contrast, a trapezoid had differing sides and interior angles, as seen in his work on the table and his responses (Lines #1–4).

By comparing the geometric properties, he could constrain a trapezoid to a parallelogram “by making two pairs of sides parallel and opposite sides equal” (Line #6). Such a focus continued with the researcher’s probing about the affordance of a trapezoid, simultaneously a constraint for the parallelogram. Note that “affordance” and “flexibility” are used interchangeably in Turkish. As a result, Efe highlighted the parallelism property of trapezoid as an affordance for trapezoid (Lines #7-#10), which made it less constrained than a parallelogram for him (Line #12). Efe now had an abstraction of the trapezoid at VH3, which we called Abstraction 4 (A#4-VH3), that included “parallelism as an affordance” that allowed the trapezoid to be constrained to a parallelogram. Based on this affordance, he could compare trapezoids and parallelograms, showing us traces of operating at the VH3 empirical level. His reflection on the constraints and affordances of both shape families and analyzing both shape families at the same time by referring to an argument like “ … is an affordance for trapezoid which is as well a constraint for parallelogram” allowed him to consider trapezoid as “more flexible” and parallelogram as “less flexible” (Line #12).

The researcher then probed Efe’s thinking about the inclusivity of the trapezoid, as illustrated in Figure 5. Data Chunk 4 reveals the further refinement of Efe’s abstraction of the trapezoid.

Figure 5. Inclusivity of trapezoid family – Data Chunk 4 (Task 3 – Time: 18:50–20:15 minutes).

Efe now abstracted the trapezoid as a structure, including the parallelogram. He did this using parallelism as an affordance for trapezoids and a constraint for parallelograms (Line #6). Efe now had an expanded understanding suggesting that the trapezoid family contained the parallelogram family because of its affordances of differing sides, angles, and at least one pair of parallel sides, which we called Abstraction 5 (A#5-VH3), suggesting operating at the VH3 level (at the componential analysis level).

Data Chunks 3 and 4 proved that Task 3 was quite promising in moving Efe to the VH3 level if the student’s attention was kept on property-based analysis of different quadrilaterals using the affordances-constraints dichotomy. In other words, Task 3, in a sense, allowed Efe to understand how an essential set of geometric properties of a quadrilateral (e.g., parallelogram) is part of or included in the geometric properties of another quadrilateral (e.g., trapezoid) in the context of affordances and constraints. Constant comparison of two quadrilaterals based on at least one pair of parallel sides versus two pairs of parallel sides properties in the context of constraints and affordances seemed to be the key that established the interrelation between trapezoids and parallelograms, paving the way to moving to VH3 level operating. Note that this came out in a paper-and-pencil environment (Task 3) following a goal-directed experience in a DGE (Task 2).

Traces of VH3 Level Thinking in the Post-Interview

During the first week following the completion of teaching sessions, we interviewed Efe to check his abstraction of quadrilateral interrelations. In the interview, Efe was given a sheet having some questions. Data Chunk 5 (see for further evidence) is a section from Efe’s post-interview. This long dialogue reveals Efe’s already established coordination of different abstractions at VH3, which can also be compared to Efe’s responses in the pre-interview.

Before the post-interview, Efe abstracted square, rhombus, rectangle, parallelogram, and trapezoid; however, we only shared his abstraction of the trapezoid and its relation to the parallelogram in this article. Data Chunk 5 provides further evidence about Efe’s abstractions at the VH3 level. Efe showed us that he had logically “organize[d] sets of properties” for different quadrilaterals so that these properties “can be meaningfully decomposed, analyzed, and applied to various shapes” (Battista, 2008, p. 139). For example, he had an abstraction of a square as having a set of properties (equal side lengths, 90-degree interior angles, two pairs of parallel sides), which were constraints for a square (Lines #4, #10, and #42 give evidence). He also had a VH3-level abstraction of a trapezoid as a quadrilateral with at least one pair of parallel sides, changing sides, changing angles (including the angle between diagonals), as well as knowing that parallelism was an affordance that allowed the inclusion of other quadrilaterals (Lines #4, #8 and #28 give additional evidence). Note that such sets of properties for squares and trapezoids operated as a totality for each quadrilateral type. Still, they could also be decomposed into individual properties to reason about interrelationships – namely, VH3 level work. By analyzing these properties through cross-comparison (Lines #4-#12), Efe could apply the “at least one pair of parallel sides” property to the square and consider it as a property that constrained a trapezoid to a square (Lines #8-#12). Such comparisons were also made for rectangle and parallelogram (Line #16), rhombus and rectangle (Lines #17–26), parallelogram and trapezoid (Lines #27–28, #35–36), rhombus and trapezoid (Lines #29–34), square, rectangle, and trapezoid (Lines #37–38), and square and parallelogram (Lines #39–44).

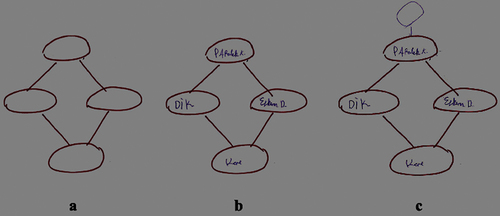
Efe’s analyses align with the hierarchical diagram he drew in the last teaching session. When asked to put these quadrilaterals into a hierarchy with a diagram as in Figure 6a, Efe placed square (at the bottom), rectangle (middle-left), rhombus (middle-right), and parallelogram (at the top) in the diagram as illustrated in Figure 6b. He finally mentioned that the trapezoid should be put on the top by drawing a different section (Figure 6c). The diagrams in Figure 6 do not include inclusively drawn sets but sets with a bottom-up hierarchy, which was the style used during the teaching sessions. This is also proof of Efe’s thinking at the VH3 level.

Figure 6. Efe’s representation of quadrilateral hierarchy (from Teaching Session 7 – Time: 25:30 minutes).

Discussion, Future Directions, and Implications

Giving students opportunities to understand the interrelations of quadrilaterals is important (Fujita & Jones, 2007). DGE (Lai & White, 2012) plays a particular role in focusing students’ attention on figure properties and better models of quadrilaterals (Erez & Yerushalmy, 2006). We revised Battista’s (2012) Shape Makers and developed a task sequence to foster a student’s abstractions of interrelations of quadrilaterals leading to a hierarchy. As detailed in the following three paragraphs, we created three sets of tasks and investigated how different parts of the task sequence fostered different abstractions.

Task 1 served Efe in helping him experiment with a drag-to-fit strategy to compare a quadrilateral (e.g., parallelogram) to its immediate successor (e.g., trapezium). Such limitation on Efe’s activity allowed him to benefit from the affordances of dragging in thinking holistically about the spatial properties rather than interrelationships between those quadrilaterals (VH2 thinking rather than VH3). Learners should understand dragging as preserving critical attributes of the preconstructed shapes (Erez & Yerushalmy, 2006). Task 1 was limited as it only encouraged Efe to focus holistically on properties and spatial aspects of given shapes with limited VH2 level thinking. In other words, Task 1 encouraged Efe to use a drag-to-fit strategy to focus on spatial aspects of given shapes with minimal property-based reasoning (A#1-VH2 and A#2-VH2). Task 1 lacked deeper reflection, experimentation (Battista, 2008), and effective teacher guidance. We also experienced that free experimentation with DGE tasks was ineffective (Erez & Yerushalmy, 2006).

Task 2 involved more teacher guidance and focused on the properties of quadrilaterals via measures. Task 2, with dragging and teacher probing, allowed Efe to zoom in on the geometric properties of the trapezoid and expand his abstraction of the trapezoid to include parallelism (A#3-VH2). However, all this depended on heavy use of dragging and teacher probing/leading and was all limited to trapezoids. Therefore, Efe could not establish interrelations leading to a hierarchy, limiting him to VH2-level operating. Asymmetry and transitivity of the relations among quadrilaterals are keys to understanding quadrilateral interrelations, as Markman (1989) pointed out, and we concur. Task 2, in this sense, was insufficient to help Efe establish the interrelations paving the way to a hierarchy, nor to help him move to VH3.

Establishing interrelations leading to a hierarchy required the student to understand “inherent attributes common to both the subset and superset in a hierarchical relationship” (Molitoris Miller, 2013, p. 273). Molitoris Miller (2013) also speculated the importance of recognizing the hierarchy among properties of shapes (stronger versus weaker properties) before abstracting the interrelations of shapes leading to a hierarchy. Our data justifies this speculation. Task 3 was quite promising in moving Efe to the VH3 level if the student’s attention was kept on property-based analysis of different quadrilaterals in the affordances-constraints dichotomy. In other words, Task 3, in a sense, allowed Efe to understand how an essential set of geometric properties parallelogram was part of or included in the geometric properties of the trapezoid in the context of affordances and constraints. Constant comparison of two quadrilaterals based on at least one pair of parallel sides versus two pairs of parallel sides properties in the context of constraints and affordances seemed to be the key that established the interrelation between trapezoid and parallelogram, paving the way to moving to VH3 level operating (A#4-VH3 and A#5-VH3). Note that this came out in a paper-and-pencil environment (Task 3) following a goal-directed experience in a DGE (Task 2). Efe’s work on Task 1 (use of drag-to-fit strategy) and Task 2 (focusing on measures) heavily depended on DGE and was insufficient to abstract interrelations at VH3. In contrast, his most sophisticated reasoning emerged during his scaffolded interactions with the teacher-researcher and paper-pencil environment (Task 3). Comparing quadrilaterals within different settings (e.g., DGE with Task 2 and, mostly, paper-pencil environment with Task 3) supported Efe’s abstraction of interrelations and moved him to the VH3 level. Therefore, we believe that it is useful to use dynamic (e.g., DGE) and static (e.g., paper-pencil) environments as complementary (Kaur, 2015; Kokol-Voljc, 2007; Komatsu & Jones, 2020). Moreover, Way (2011) highlights the affordances of digital resources as an advantage over non-digital resources. We found that these affordances might support student understanding if the teacher simultaneously encouraged the student to evaluate quadrilaterals’ affordances and constraints in DGE and paper-pencil environments.

Apart from the tasks and their sequence, the order in which we helped Efe investigate the shape families was also important. Studies about the development of quadrilaterals in a hierarchical manner either used or recommended task sequences that adopt a top-down approach (e.g., Craine & Rubenstein, 1993), starting teaching with trapezoid going down to the square. Battista (2012) also used all quadrilateral makers simultaneously in his designed tasks. In DGE, tracking the visual changes and attending to invariances among the geometric properties simultaneously is complex (Erez & Yerushalmy, 2006). Therefore, as detailed previously, we used a bottom-up approach (as shown in Table 2 and Figure 1), starting with squares and moving up in the hierarchy with one successor quadrilateral at a time. Such an approach allowed us to focus Efe’s attention on the constraints and affordances of the properties of each quadrilateral in a way that led to a hierarchy of relations and quadrilaterals, or VH3 level thinking. Efe’s understanding of trapezoids and their relation to parallelograms slowly evolved from VH2 abstractions (a trapezoid having oblique and unequal sides, a trapezoid with affordances of changing sides and angles, a trapezoid with changing sides/angles and at least a pair of parallel sides) to VH3 abstractions (parallelism as an affordance for trapezoid, a trapezoid with all its affordances). The developed task sequence consisted of a Guess-Check activity in DGE (Task 1), the investigation of shape families in DGE (without measures and with measures – Task 2), and the investigation of the same family properties on paper with teacher scaffolding (Task 3). In contrast to Shape Makers (Battista, 2012), our task design choices about a bottom-up approach focusing on two-three shape families at a time, continuous constraint-affordance focus, and constant attention to asymmetry and transitivity of properties for inclusion also contributed to such progress. Even though we provided a very limited picture from one student’s data for two quadrilaterals only, we believe this article provides initial evidence for the classification process (De Villiers, 1994) and the effect of such choices on Efe’s developing understanding from VH2 to VH3. In this sense, this study can inform future curriculum design efforts in geometry. Using such an ordered task sequence as a package effectively fostered a student’s abstraction of interrelations of quadrilaterals leading to a hierarchy at the VH3 level. The sequence used an approach aligned with constructivist principles (action, reflection, abstraction), which can also guide teachers in helping their students move from isolated quadrilaterals (VH2 level thinking) to ones having inclusion relations (VH3 level thinking).

Battista (2007, p. 867) mentioned, “In analyzing draggable drawings, students first notice movement constraints, then later, they might conceptualize these constraints in terms of regularities or invariants, and finally, and often only with great effort, these constraints are conceptualized as formal geometric properties.” We observed the same progression since Task 1 was about movement constraints, Task 2 was about regularities and invariants in geometry and measurement, and Task 3 was for conceptualizing constraints as formal geometric properties. We found such ordering compelling; however, we realized that abstracting interrelations was feasible when the student was constantly probed to think about asymmetry and transitivity of properties by referring to constraint-affordance dichotomy. Our design heavily used the constraint-affordance dichotomy as a task design element and comparison tool. Encouraging the student to focus on the constraints and affordances of a shape family and its successor simultaneously (as in Task 3) to compare two shape families based on asymmetry and transitivity properties was key in helping Efe move from VH2-level thinking to VH3-level thinking. Simultaneously paying attention to the constraints and affordances of two families in a successive hierarchy allowed Efe to focus on varying or invariant properties of those two families and establish a hierarchy at VH3. Such a method also helped the teacher-researcher to keep the student’s attention on property-based commonalities or differences of successive shape families. This is how our study deviated from others (e.g., Battista, 2012; Gal & Lew, 2008; Lai & White, 2012; Leung, 2008).

As mentioned previously, we only shared an example of what it means to develop the interrelation between parallelograms and trapezoids using a single student’s case in this article. We were also limited to using five quadrilaterals in our task design and to the teaching experiment of a single student. In this sense, our findings are limited and cannot be generalized. However, they can be used to inform future curriculum development efforts, as detailed previously. What is yet to be investigated is the task development for students entering the teaching at various van Hiele levels or primary school levels, the balance between the use of DGE and paper-pencil environments, and applications in actual classroom settings. Future research efforts without the abovementioned limitations would better inform our understanding of these issues.

Acknowledgement

The data provided in this paper comes from the master's dissertation study of the second author (Gürhan, 2015) supervised by the first author.

Disclosure statement

No potential conflict of interest was reported by the authors.

Supplementary Material

Supplemental data for this article can be accessed online at https://doi.org/10.1080/19477503.2023.2209430

Notes

¹ Note that throughout the paper, we consider an inclusive definition of trapezoid: a trapezoid is “a quadrilateral with at least one pair of parallel sides” (Usiskin & Griffin, 2008, p. 27).

² If all geometric properties of Class A fall into Class B, then Class B includes Class A but not vice versa.

³ If all the geometric properties of Class A are part of Class B and if all geometric properties of Class B are part of Class C, then Class A is included in Class C.

⁴ Note that we use capital letters when referring to Battista’s curriculum and lowercase when referring to the generic shapes used in the DGE.

⁵ Note that there are different types of abstraction defined in the literature. Piaget (2001) defined empirical, reflecting, and reflective abstractions, whereas Battista (2008) defined spatial (corresponding to van Hiele Level 1), geometric (corresponding to van Hiele Level 2), and logical structuring (corresponding to van Hiele Level 3) as different abstractions. In this paper, instead of highlighting those different types, we used the given abstraction definition as an orienting frame and focused on van Hiele levels as different levels of abstraction.

Appendix

Pre- and Post-Interview Questions

Table

Section 1	Section 2	Section 3
1. Which of the following shapes is/are square?	1. What is a square? What are its most basic properties?	1. Is a square a trapezium?
		2. Is a rhombus a rectangle?
2. Which of the following shapes is/are rectangle?	2. What is a rectangle? What are its properties?	3. Is a rhombus a trapezium?
		4. Is a rectangle a parallelogram?
3. Which of the following shapes is/are rhombus?	3. What is a rhombus? What are its properties?	We asked the following two additional questions in post-interview only: 5. Is a trapezium a parallelogram? 6. Is a parallelogram a square?
4. Which of the following shapes is/are parallelogram?	4. If you wanted to tell a friend about the parallelogram, how would you do it? What properties must a shape have for it to be a parallelogram?
5. Which of the following shapes is/are trapezium?	5. What is a trapezium? What are its properties?

Note that the students went through all the questions in Section 1, Section 2, and Section 3, respectively.