Event-triggered control for trajectory tracking of quadrotor unmanned aerial vehicle

Abstract

This paper studies the trajectory tracking problem of quadrotor unmanned aerial vehicle (QUAV) with model nonlinearities and external disturbances via event-triggered control technique. Dividing the QUAV system into position subsystem and attitude subsystem, an adaptive fuzzy control algorithm is designed in position subsystem to provide desired pitch and roll angles for the attitude subsystem. Then, by constructing an event-triggered mechanism, an event-triggered adaptive fuzzy control algorithm is presented in the attitude subsystem, where the control law and the fuzzy parameter adaptive law are updated in an aperiodic form. Based on Lyapunov stability theory, it is proved that all signals in the closed-loop system are uniformly ultimately bounded via the impulsive dynamical system tool, and the tracking errors converge to a small neighbourhood of the origin. Besides, it is proved that there is a positive lower bound between the intersample time to avoid Zeno behaviour. Finally, simulation results illustrate that the proposed control scheme can guarantee the trajectory tracking performance of the QUAV system, while it can reduce the update frequency of the controller and improve the resource utilization.

Keywords:

• Adaptive fuzzy control
• event-triggered control
• quadrotor unmanned aerial vehicle
• trajectory tracking

1. Introduction

Recently, QUAV has been widely applied in various fields, such as transportation, video surveillance, business performance and post-disaster rescue. In these areas, it is often required to achieve accurate tracking performance (Adlakha & Zheng, 2020). However, QUAV is an under-actuated and multi-input multi-output system with nonlinearities and strong coupling characteristics. The uncertain terms together with external disturbances have great affect on the tracking performance. Thus, it is more challenging to design the tracking control algorithms of QUAV (Özbek et al., 2015).

Numerous research results on the trajectory tracking of QUAV are available (Antonio-Toledo et al., 2018; Chen et al., 2016; Choi & Ahn, 2015; Emam & Fakharian, 2016; Liu et al., 2016). For example, a set point tracking control is presented for QUAV with known dynamics via the feedback linearization method in Choi and Ahn (2015). A sliding mode controller is designed for QUAV with uncertain parameters and external disturbances in Chen et al. (2016) and Antonio-Toledo et al. (2018). Robust compensation technique is introduced to restrain the model uncertainties and external disturbance in Liu et al. (2016). Hybrid robust H and $H_{\mathrm{\infty }}$ controllers are constructed to suppress the influence of measurement noise and external disturbances based on LMI method in Emam and Fakharian (2016). In addition, adaptive trajectory control algorithms are proposed to identify the upper bounds of unknown parameters and external disturbances in Zuo (2013), Antonelli et al. (2017) and Wang et al. (2017). State estimation technique is adopted to QUAV systems (Luo et al., 2021, 2020). In Zhang et al. (2020), Ai and Yu (2020) and Zhang, J. Q. et al. (2019), trajectory tracking control methods based on active disturbance rejection control are proposed by introducing disturbance observers and extended state observers.

The intelligent adaptive control based on fuzzy logic systems (FLSs) or neural networks (NNs) becomes an effective tool to solve the control problem of uncertain nonlinear systems (Li et al., 2010; Tong et al., 2014; Wang & Huang, 2005). An adaptive NN position tracking controller based on backstepping recursive technique is designed in Ariffanan and Basri (2018), where the time-varying external disturbances are approximated by NNs and the controller parameters are optimized by gravitational search algorithm. Using FLSs to approximate unknown external disturbances, an adaptive fuzzy position tracking control algorithm is presented in Xu et al. (2019). In the work (Zhou et al., 2018), an adaptive NN finite-time tracking control algorithm is proposed, which can effectively restrain the influence of input saturation on the control performance. By introducing a fuzzy state observer to estimate the system states, an adaptive fuzzy output feedback trajectory tracking control is designed in Mallavalli and Fekih (2020) and Wang and Wang (2018). Despite some effective control algorithms are developed for the trajectory tracking of QUAV, most of the aforementioned control algorithms are continuously updating, even though it has achieved satisfactory control performance.

In practical application, the control algorithm of QUAV is implemented by airborne embedded micro processing unit. Therefore, the continuous control algorithms or the fixed period updating control algorithms will increase the processor computation, which will further lead to the redundant communication and energy consumption. Note that event-triggered control (ETC) has been receiving increased attention and fruitful theoretical researches have been developed (Li, Alsaadi et al., 2020; Li, Wang et al., 2020; Li & &Yang, 2018; Postoyan et al., 2015; Xing et al., 2017). The ETC algorithm is updated in an aperiodic form according to the performance index while maintaining satisfied control performance. On the above basis, the trajectory tracking control problem of QUAV based on ETC is studied in Zhang, J. Q. et al. (2019), Wang et al. (2019) and Wang et al. (2020). In Zhang, M. et al. (2019), using weight multi-model method to model the nonlinear QUAV system, a position tracking controller is designed based on LMI technique, and an event-triggered mechanism is designed to determine the update instants of control signal. Robust sliding mode controllers are proposed both in the position and attitude loop to eliminate the external disturbances in Wang et al. (2019), where the attitude tracking controller is updated in an aperiodic form based on the event-triggered mechanism. In Wang et al. (2020), a robust adaptive attitude tracking controller based on ETC is proposed, where the upper bound of the external disturbance is estimated via the adaptive control technique. It is worth pointing out that the mentioned ETC based trajectory tracking control algorithms limit to QUAV with known dynamics. To our best knowledge, it is still an open problem for the intelligent adaptive ETC based on the trajectory tracking of QUAV with unknown dynamics and external disturbances, which motivates our research.

Based on the above research results, this paper proposes an adaptive fuzzy trajectory tracking control algorithm based on ETC technique for QUAV with model nonlinearities and external disturbances. In the control design, an adaptive fuzzy position tracking control is designed first. Then, an adaptive event-triggered mechanism is constructed in the attitude subsystem, and an event-triggered adaptive fuzzy attitude tracking control is developed. The contributions are summarized as follows.

1. In this article, an event-triggered mechanism is introduced in the attitude control loop to determine the instants of information transmission. Based on the designed event-triggered mechanism, the adaptive fuzzy attitude tracking controller is updated only when the prescribed error exceeds a given threshold, which is different from the continuously updating control algorithms given in Zuo (2013), Antonelli et al. (2017), Wang et al. (2017), Zhang et al. (2020), Ai and Yu (2020), Zhang, M. et al. (2019), Ariffanan and Basri (2018), Xu et al. (2019), Zhou et al. (2018), Mallavalli and Fekih (2020) and Wang and Wang (2018). Under the proposed control protocol, the QUAV system can achieve satisfactory control performance while the calculation cost and communication pressure are greatly reduced.

2. By utilizing FLSs to identify the lumped nonlinearities online, an event-triggered adaptive fuzzy tracking control is developed for QUAV with model nonlinearities and external disturbances. Note that the existing ETC algorithms in Zhang, M. et al. (2019), Wang et al. (2019) and Wang et al. (2020) require the precise model information of QUAV. Besides, an adaptive event-triggered mechanism is constructed based on measurement error and the fuzzy adaptive parameters in this article, and both the controller and the adaptive parameter in the attitude control loop are updated in an aperiodic form under the designed event-triggered mechanism, while the adaptive parameter is continuously updated under the event-triggered mechanism in Wanget al. (2020).

2. Problem description

2.1. The model of the QUAV

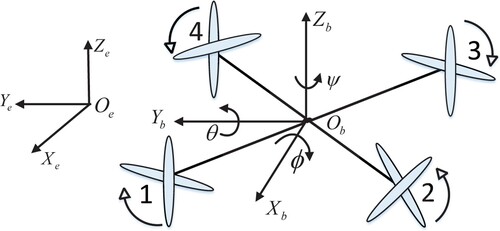
In Figure 1, take the four machine arms intersection $O_b$ as the coordinate centre, then the body coordinate of the ‘X’ type QUAV system $O_b{X}_b{Y}_b{Z}_b$ can be built, where $X_b$ axis is points to the forward direction of the nose, $Z_b$ axis is points to the opposite extension of the earth's centre and the positive direction of the $Y_b$ axis is determined by the right-hand rule.

Figure 1. The coordinate of the QUAV system.

Take the QUAV take-off position $O_e$ as the origin of the earth coordinate system $O_e{X}_e{Y}_e{Z}_e$, where the direction of the $X_e$ axis points to the East, the direction of the $X_e$ axis points to the reverse extension line of the $Z_e$ axis which pointing to the earth centre, and the direction of the $O_e$ axis is determined by the right-hand rule.

The position coordinate and the attitude coordinate of QUAV are established under the earth coordinate and the body coordinate, respectively. The two coordinates can be transformed through the rotation matrix. The position subsystem and the attitude subsystem of QUAV will be established respectively for analysis in this section.

The mathematical model of the QUAV position subsystem can be expressed as Wang et al. (2017) (1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) where (2) $\begin{array}{rl}{G}_2\left({\eta }_1,{\eta }_2,t\right)& =F_1\left({\eta }_2\right)+d_1\left({\eta }_1,{\eta }_2,t\right)\end{array}$(2) (3) $\begin{array}{rl}{U}_1\left({\eta }_3,{\tau }_1\right)& =\frac{{\tau }_1}{m}\left[\begin{array}{l}\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi \\ \cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi \\ \cos \varphi \cos \theta \end{array}\right]\end{array}$(3) (4) $\begin{array}{rl}{F}_1\left({\eta }_2\right)& =\left[\begin{array}{c}-k_f\dot{x}/m\\ -k_f\dot{y}/m\\ -k_f\dot{z}/m-g\end{array}\right]\end{array}$(4) ${\eta }_1={\left[x,y,z\right]}^T$ and ${\eta }_2={\left[\dot{x},\dot{y},\dot{z}\right]}^T$ denote the position vector and velocity vector of the QUAV. $U_1={\left[u_{11},u_{12},u_{13}\right]}^T$ is the input of the position subsystem, ${\tau }_1$ represents the sum of the lift generated by the four rotors. ${\eta }_3={\left[\psi ,\theta ,\varphi \right]}^T$ is the Euler angle vector, where ψ, θ, ϕ are the yaw, pitch and roll angle, which rotate around the Z, Y and X axes respectively. The nonlinear external disturbance is express as $d_1={\left[d_{11},d_{12},d_{13}\right]}^T$. Moreover, $k_f$, m, g are the air damping coefficient, the mass of the QUAV and the acceleration of the gravity.

The mathematical model of the QUAV attitude subsystem can be expressed as (5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) where (6) $\begin{array}{rl}{G}_4\left({\eta }_3,{\eta }_4,t\right)& =F_3\left({\eta }_4\right)+d_3\left({\eta }_3,{\eta }_4,t\right)\end{array}$(6) (7) $\begin{array}{rl}{F}_3\left({\eta }_4\right)& =\left[\begin{array}{l}{\displaystyle \frac{I_{xx}-I_{yy}}{I_{zz}}\dot{\theta }\dot{\varphi }}\\ {\displaystyle \frac{I_{zz}-I_{xx}}{I_{yy}}\dot{\psi }\dot{\varphi }}\\ {\displaystyle \frac{I_{yy}-I_{zz}}{I_{xx}}\dot{\psi }\dot{\theta }}\end{array}\right]\end{array}$(7) ${\eta }_4={\left[\dot{\psi },\dot{\theta },\dot{\varphi }\right]}^T$ and ${\text{U}}_3\text{ = }{\left[{\tau }_2,{\tau }_3,{\tau }_4\right]}^T$ denote the angular velocity vector and the input torque vector of the attitude subsystem. The nonlinear external disturbance is express as $d_3=[d_{31},d_{32},d_{33}{]}^T$. Moreover, $M_3=$diag$\{l/I_{zz},l/I_{yy},l/I_{xx}\}$ and l is the inertia matrix of the QUAV and the distance from one of the four motors to the centre of the QUAV.

2.2. Fuzzy logic system

An FLS consists of the knowledge base, the fuzzifier, the fuzzy inference engine and the defuzzifier. The fuzzy inference engine comprises a collection of the following if-then rules: $R^v:IF{x}_{1}is{E}_1^v\mathrm{and}\dots x_{n}is{E}_n^v,THENyis{J}^v$where $x=[x_1,\dots ,x_n{]}^T\in R^n$ and $y\in R$ are the FLS input and output, respectively. $E_h^v(h=1,\dots ,n)$ and $J^v$ represent fuzzy sets. $v=1,2,\dots ,N$, where N represents the number of the rules. Through singleton function, centre average defuzzification and product inference, the FLS can be expressed as (8) $\begin{array}{r}y\left(x\right)=\frac{{\sum }_{v=1}^N\underset{-}{y_v}\prod _{h=1}^n{\mu }_{E_h^v}(x_h)}{\sum {}_{v=1}^N\left[\prod _{h=1}^n{\mu }_{E_h^v}(x_h)\right]}\end{array}$(8) where ${\mu }_{E_h^v}(x_h)$ and ${\mu }_{J^v}(y)$ are the fuzzy functions of the $E_h^v$ and $J^v$, $\underset{-}{y_v}=\underset{y\in R}{max}{\mu }_{J^v}(y)$. Define the fuzzy basis function as (9) $\begin{array}{r}{\phi }_v=\frac{\prod _{h=1}^n{\mu }_{E_h^v}(x_h)}{\sum {}_{v=1}^N\left[\prod _{h=1}^n{\mu }_{E_h^v}(x_h)\right]}\end{array}$(9) By choosing $W={\left[\underset{-}{y_1},\underset{-}{y_2},\dots ,\underset{-}{y_N}\right]}^T$ and $\phi \left(x\right)=[{\rho }_1\left(x\right),{\rho }_2\left(x\right),\dots ,{\rho }_N\left(x\right){]}^T$, the FLS can be expressed as (10) $\begin{array}{r}y\left(x\right)=W^T\phi \left(x\right)\end{array}$(10)

Lemma 2.1

Let $f(x)$ be a continuous function defined on a compact set ${\mathrm{\Xi }}_f\in R^n$. Then for any constant $\epsilon >0$, there exists an FLS such as (11) $\begin{array}{r}\underset{x\in \mathrm{\Xi }}{sup}\left|f\left(x\right)-W^T\phi \left(x\right)\right|\le \epsilon \end{array}$(11)

According to Lemma 2.1, the unknown nonlinear part $G_2\left({\eta }_1,{\eta }_2,t\right)$ and $G_4\left({\eta }_3,{\eta }_4,t\right)$ of the position subsystem (1(1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) ) and the attitude subsystem (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ) can be approximated by an FLS as follows. (12) $\begin{array}{r}{G}_j=W_{G_j}^{\ast T}{\phi }_j\left(H_j\right)+{\epsilon }_{G_j},j=2,4\end{array}$(12) where $W_{G_j}^{\ast }$ and ${\phi }_j\left(H_j\right)=[{\rho }_{j1}\left(H_j\right),\dots ,{\rho }_{jN}\left(H_j\right){]}^T$ represent the optimal parameter vector and the fuzzy basis function vector. Moreover, the minimum fuzzy approximation errors ${\epsilon }_{G_j}$ satisfies the unequal formula $\Vert {\epsilon }_{G_j}\Vert \le {\delta }_{G_j}$, where ${\delta }_{G_j}$ are the arbitrary positive constants in the compact set ${\mathrm{\Xi }}_{\delta }$, and ${\mathrm{\Xi }}_W$ and ${\mathrm{\Xi }}_H$ are the compact sets of the $W_{G_j}$ and $H_{{}_j}$.

Assumption 2.1

The given desired trajectory ${\eta }_{1d}={\left[x_d,y_d,z_d\right]}^T$ and the desired yaw angle ${\psi }_d$ are known and their first and second derivatives are bounded.

Assumption 2.2

The fuzzy basis function vector ${\phi }_4\left({\mathrm{H}}_4\right)$ satisfies the global Lipschitz continuity condition, such that $\Vert {\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\Vert \le L_4\Vert {\mathrm{H}}_4-{\overline{\mathrm{H}}}_4\Vert$, where $L_4$ is the known constants.

Remark 2.1

Assumption 2.1 is a reasonable and mild assumption, since in the trajectory tracking of QUAV, the desired trajectory and yaw angle always change in a certain region. Assumption 2.2 indicates that the fuzzy basis function vector satisfies the local Lipschitz continuity condition. It is a common assumption in fuzzy or NN-based control design. Similar assumption can also be found in Tong et al. (2014).

3. Adaptive fuzzy position tracking control design

In this section, an adaptive fuzzy trajectory tracking control algorithm will be performed in the position loop based on backstepping control technique.

Step 3.1

Define the position tracking error vector for the subsystem (1(1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) ) as (13) $\begin{array}{r}{e}_1={\eta }_1-{\eta }_{1d}.\end{array}$(13) Differentiating (13(13) $\begin{array}{r}{e}_1={\eta }_1-{\eta }_{1d}.\end{array}$(13) ) along with (1(1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) ), we have (14) $\begin{array}{r}{\dot{e}}_1={\eta }_2-{\dot{\eta }}_{1d}.\end{array}$(14) The virtual control law is designed as (15) $\begin{array}{r}{\alpha }_1=-K_1{e}_1+{\dot{\eta }}_{1d},\end{array}$(15) where $K_1=\mathrm{diag}\left\{p_{11},p_{12},p_{13}\right\}>0$ is the gain matrix.

Let ${\alpha }_1$ pass through a first-order filter to obtain the filtered output ${\alpha }_{1f}$: (16) $\begin{array}{r}{\chi }_1{\dot{\alpha }}_{1f}+{\alpha }_{1f}={\alpha }_1,{\alpha }_{1f}(0)={\alpha }_1(0),\end{array}$(16) where ${\chi }_1$ is filter time constant. Then, the filter error is constructed as (17) $\begin{array}{r}{e}_f={\alpha }_{1f}-{\alpha }_1.\end{array}$(17) From (16(16) $\begin{array}{r}{\chi }_1{\dot{\alpha }}_{1f}+{\alpha }_{1f}={\alpha }_1,{\alpha }_{1f}(0)={\alpha }_1(0),\end{array}$(16) ) and (17(17) $\begin{array}{r}{e}_f={\alpha }_{1f}-{\alpha }_1.\end{array}$(17) ), we obtain (18) $\begin{array}{r}{\dot{e}}_f=-\frac{e_f}{{\chi }_1}-{\dot{\alpha }}_1.\end{array}$(18) Considering (15(15) $\begin{array}{r}{\alpha }_1=-K_1{e}_1+{\dot{\eta }}_{1d},\end{array}$(15) ) and (17(17) $\begin{array}{r}{e}_f={\alpha }_{1f}-{\alpha }_1.\end{array}$(17) ), (14(14) $\begin{array}{r}{\dot{e}}_1={\eta }_2-{\dot{\eta }}_{1d}.\end{array}$(14) ) can be rewritten as (19) $\begin{array}{r}{\dot{e}}_1=e_2+e_f+{\alpha }_1-{\dot{\eta }}_{1d},\end{array}$(19) where $e_2$ will be given in the next step.

Step 3.2

The error surface at this step is chosen as (20) $\begin{array}{r}{e}_2={\eta }_1-{\alpha }_{1f}.\end{array}$(20) Differentiating (20(20) $\begin{array}{r}{e}_2={\eta }_1-{\alpha }_{1f}.\end{array}$(20) ) along with (1(1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) ) and (12(12) $\begin{array}{r}{G}_j=W_{G_j}^{\ast T}{\phi }_j\left(H_j\right)+{\epsilon }_{G_j},j=2,4\end{array}$(12) ) yields (21) $\begin{array}{r}{\dot{e}}_2=W_{G_2}^{\ast T}{\phi }_2\left({\mathrm{H}}_2\right)+U_1+{\epsilon }_{G_2}-{\dot{\alpha }}_{1f},\end{array}$(21) where ${\mathrm{H}}_2=[{\eta }_1,{\eta }_2,d_1{]}^T$ is the fuzzy basis function vectors.

The actual control law $U_1$ is constructed as (22) $\begin{array}{r}{U}_1=-{\hat{W}}_{G_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-K_2{e}_2+{\dot{\alpha }}_{1f},\end{array}$(22) where $K_2=$diag$\left\{p_{21},p_{22},p_{23}\right\}>0$ is the gain matrix. ${\hat{W}}_{G_2}$ is the estimation of $W_{G_2}^{\ast }$.

The updated law of ${\hat{W}}_{G_2}$ is designed as (23) $\begin{array}{r}{\dot{\hat{W}}}_{G_2}={\mathrm{\Delta }}_2({e_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-a_2{\hat{W}}_{G_2}),\end{array}$(23) where ${\mathrm{\Delta }}_2>0$ and $a_2>0$ are design constants.

4. Event-triggered adaptive fuzzy attitude tracking control design

The adaptive fuzzy attitude tracking controller is updated only when an event occurs. Hence, zero-order hold (ZOH) is used to retain the last event-sampled state. The event-triggered error is defined as (24) $\begin{array}{r}{s}_i\left(t\right)={\eta }_i\left(t\right)-{\overline{\eta }}_i\left(t\right),i=3,4\end{array}$(24) where ${\eta }_i\left(t\right)(i=3,4)$ is the current measured state vector and ${\overline{\eta }}_i\left(t\right)$ is the state vector held by the ZOH.

The error between the current external disturbance $d_3$ and the external disturbance held by the ZOH ${\overline{d}}_3$ is defined as (25) $\begin{array}{r}{s}_{cs}\left(t\right)=d_3\left(t\right)-{\overline{d}}_3\left(t\right).\end{array}$(25) Let ${\left\{t_k\right\}}_{k=1}^{\mathrm{\infty }}$,($k\in Z^{+}$) be a monotonically increasing sequence of the triggering instants, and the first triggering instant occurs at $t_0=0$. Then, the state vectors ${\overline{\eta }}_i\left(t\right)$ held by the ZOH can be expressed as (26) $\begin{array}{r}\{\begin{array}{l}{\overline{\eta }}_i\left(t^{+}\right)={\eta }_i\left(t_k\right),\mathrm{t}={\mathrm{t}}_k\\ {\overline{\eta }}_i\left(t\right)={\eta }_i\left(t_k\right),{\mathrm{t}}_k\le \mathrm{t}<{\mathrm{t}}_{k+1}\end{array}\end{array}$(26) To proceeding to the design of the attitude tracking controller, considering (3(3) $\begin{array}{rl}{U}_1\left({\eta }_3,{\tau }_1\right)& =\frac{{\tau }_1}{m}\left[\begin{array}{l}\cos \varphi \sin \theta \cos \psi +\sin \varphi \sin \psi \\ \cos \varphi \sin \theta \sin \psi -\sin \varphi \cos \psi \\ \cos \varphi \cos \theta \end{array}\right]\end{array}$(3) ) and (22(22) $\begin{array}{r}{U}_1=-{\hat{W}}_{G_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-K_2{e}_2+{\dot{\alpha }}_{1f},\end{array}$(22) ), we obtain the sum of the QUAV lift force as (27) $\begin{array}{r}{\tau }_1=m\Vert U_1\Vert .\end{array}$(27) Then, the desired roll angle ${\varphi }_d$ and the desired pitch angle ${\theta }_d$ can be obtained by inverse solving (3) as (28) $\begin{array}{rl}{\varphi }_d& =\arcsin \left(\frac{m}{{\tau }_1}{u}_{11}\sin {\psi }_d-\frac{m}{{\tau }_1}{u}_{12}\cos {\psi }_d\right),\end{array}$(28) (29) $\begin{array}{rl}{\theta }_d& =\arcsin \left(\frac{\frac{m}{{\tau }_1}{u}_{11}-\sin {\varphi }_d\sin {\psi }_d}{\cos {\varphi }_d\cos {\psi }_d}\right).\end{array}$(29) Now, we are in the position of designing the attitude tracking controller.

Step 1. Define the attitude tracking error vector as (30) $\begin{array}{r}{e}_3={\eta }_3-{\eta }_{3d},\end{array}$(30) where ${\eta }_{3d}={\left[{\psi }_d,{\theta }_d,{\varphi }_d\right]}^T$.

Differentiating (30(30) $\begin{array}{r}{e}_3={\eta }_3-{\eta }_{3d},\end{array}$(30) ) along with (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ), we have (31) $\begin{array}{r}{\dot{e}}_3={\eta }_4-{\dot{\eta }}_{3d}.\end{array}$(31) The event-triggered virtual control law during $(t_k\le t<t_{k+1},k\in Z^{+})$ is constructed as (32) $\begin{array}{r}{\alpha }_2=-K_3{\overline{e}}_3,\end{array}$(32) where $K_3=\mathrm{diag}\left\{p_{31},p_{32},p_{33}\right\}>0$ is the gain matrix. Moreover, ${\overline{e}}_3={\overline{\eta }}_3-{\eta }_{3d}\left(t_k\right)$, so we obtain (33) $\begin{array}{r}{\dot{\overline{e}}}_3=0\end{array}$(33) Substituting (32(32) $\begin{array}{r}{\alpha }_2=-K_3{\overline{e}}_3,\end{array}$(32) ) into (31(31) $\begin{array}{r}{\dot{e}}_3={\eta }_4-{\dot{\eta }}_{3d}.\end{array}$(31) ) and considering (24(24) $\begin{array}{r}{s}_i\left(t\right)={\eta }_i\left(t\right)-{\overline{\eta }}_i\left(t\right),i=3,4\end{array}$(24) ) yields (34) $\begin{array}{r}{\dot{e}}_3=e_4+K_3{s}_3-K_3{e}_3+{\dot{\eta }}_{3d}+K_3({\eta }_{3d}-{\eta }_{3d}(t_k)),\end{array}$(34) where $e_4$ will be given in the next step.

Step 2. The error surface at this step is chosen as (35) $\begin{array}{r}{e}_4={\eta }_4-{\alpha }_2.\end{array}$(35) Differentiating (35(35) $\begin{array}{r}{e}_4={\eta }_4-{\alpha }_2.\end{array}$(35) ) along with (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ) and (12(12) $\begin{array}{r}{G}_j=W_{G_j}^{\ast T}{\phi }_j\left(H_j\right)+{\epsilon }_{G_j},j=2,4\end{array}$(12) ), we obtain (36) $\begin{array}{r}{\dot{e}}_4=W_{G_4}^{\ast T}{\phi }_4\left({\mathrm{H}}_4\right)+M_3{U}_3+{\epsilon }_{G_4},\end{array}$(36) where ${\mathrm{H}}_4=[{\eta }_3,{\eta }_4,d_3{]}^T$.

The event-triggered actual control law $U_3$ during $(t_k\le t<t_{k+1},k\in Z^{+})$ is constructed as (37) $\begin{array}{r}{U}_3=M_3^{-1}\left(-{\hat{W}}_{G_4}^T{\phi }_4\left({\overline{\mathrm{H}}}_4\right)-K_4{\overline{e}}_4\right),\end{array}$(37) where $K_4=\left\{p_{41},p_{42},p_{43}\right\}>0K_4=\left\{p_{41},p_{42},p_{43}\right\}>0$ is the gain matrix. ${\hat{W}}_{G_4}$ is the estimation of $W_{G_4}^{\ast }$. ${\overline{\mathrm{H}}}_4=[{\overline{\eta }}_3,{\overline{\eta }}_4,{\overline{d}}_3{]}^T$. ${\overline{e}}_4={\overline{\eta }}_4-{\alpha }_2$. Then, we have (38) $\begin{array}{r}{\dot{\overline{e}}}_4=0.\end{array}$(38) From (24(24) $\begin{array}{r}{s}_i\left(t\right)={\eta }_i\left(t\right)-{\overline{\eta }}_i\left(t\right),i=3,4\end{array}$(24) ) and (37(37) $\begin{array}{r}{U}_3=M_3^{-1}\left(-{\hat{W}}_{G_4}^T{\phi }_4\left({\overline{\mathrm{H}}}_4\right)-K_4{\overline{e}}_4\right),\end{array}$(37) ), (36(36) $\begin{array}{r}{\dot{e}}_4=W_{G_4}^{\ast T}{\phi }_4\left({\mathrm{H}}_4\right)+M_3{U}_3+{\epsilon }_{G_4},\end{array}$(36) ) is given by (39) $\begin{array}{rl}{\dot{e}}_4& =K_4{s}_4-K_4{e}_4\\ & +{\hat{W}}_{G_4}^T\left[{\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\right]+{\tilde{W}}_{G_4}^{{}^T}{\phi }_4\left({\mathrm{H}}_4\right)+{\epsilon }_{G_4},\end{array}$(39) where ${\tilde{W}}_{G_4}=W_{G_4}^{\ast }-{\hat{W}}_{G_4}$.

The updated law of fuzzy parameter vector ${\hat{W}}_{G_4}$ is designed as (40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) where ${\hat{W}}_{G_4}^{+}$ is the adaptive law at the triggering instants. $b_4>0c_4>0b_4>0c_4>0$, ${\kappa }_4>0$, ${\kappa }_4>0$ are the design parameters.

5. Stability analysis

In this section, the stability of the QUAV position subsystem is first provided. Then, the boundedness of parameter estimate error ${\tilde{W}}_{G_4}$ is analyse, and the stability of the QUAV attitude subsystem is given. Finally, the Zeno phenomenon is excluded under the proposed trajectory tracking control algorithm.

5.1. Stability analysis of the position loop

Theorem 5.1

Consider the nonlinear QUAV position model (1(1) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_1={\eta }_2\\ {\dot{\eta }}_2=G_2\left({\eta }_1,{\eta }_2,t\right)+U_1\left({\eta }_3,{\tau }_1\right)\end{array}\end{array}$(1) ) satisfying Assumption 2.1, the virtual control law (15(15) $\begin{array}{r}{\alpha }_1=-K_1{e}_1+{\dot{\eta }}_{1d},\end{array}$(15) ); the actual control law (22(22) $\begin{array}{r}{U}_1=-{\hat{W}}_{G_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-K_2{e}_2+{\dot{\alpha }}_{1f},\end{array}$(22) ), and the fuzzy parameter updating law (23(23) $\begin{array}{r}{\dot{\hat{W}}}_{G_2}={\mathrm{\Delta }}_2({e_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-a_2{\hat{W}}_{G_2}),\end{array}$(23) ). Then, the trajectory tracking errors are uniformly ultimately bounded.

Proof.

Defined the Lyapunov function of the position loop as (41) $\begin{array}{r}{V}_{pos}=\frac{1}{2}{e}_1^T{e}_1+\frac{1}{2}{e}_2^T{e}_2+\frac{1}{2}{e}_f^T{e}_f+\frac{1}{2{\mathrm{\Delta }}_2}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}\end{array}$(41) Differentiate (41(41) $\begin{array}{r}{V}_{pos}=\frac{1}{2}{e}_1^T{e}_1+\frac{1}{2}{e}_2^T{e}_2+\frac{1}{2}{e}_f^T{e}_f+\frac{1}{2{\mathrm{\Delta }}_2}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}\end{array}$(41) ) along with (19(19) $\begin{array}{r}{\dot{e}}_1=e_2+e_f+{\alpha }_1-{\dot{\eta }}_{1d},\end{array}$(19) ) and (21(21) $\begin{array}{r}{\dot{e}}_2=W_{G_2}^{\ast T}{\phi }_2\left({\mathrm{H}}_2\right)+U_1+{\epsilon }_{G_2}-{\dot{\alpha }}_{1f},\end{array}$(21) ) yields (42) $\begin{array}{rl}{\dot{V}}_{pos}& =e_1^T(e_2+e_f+{\alpha }_1-{\dot{\eta }}_{1d})+e_2^T[W_{G_2}^{\ast T}{\phi }_2\left({\mathrm{H}}_2\right)\\ & +U_1+{\epsilon }_{G_2}-{\dot{\alpha }}_{1f}]+e_f^T{\dot{e}}_f-\frac{1}{{\mathrm{\Delta }}_2}{\tilde{W}}_{G_2}^T{\dot{\hat{W}}}_{G_2}.\end{array}$(42) It follows from (18(18) $\begin{array}{r}{\dot{e}}_f=-\frac{e_f}{{\chi }_1}-{\dot{\alpha }}_1.\end{array}$(18) ) that (43) $\begin{array}{r}\Vert {\dot{e}}_f+\frac{e_f^{}}{{\chi }_1}\Vert =\Vert {\dot{\alpha }}_1\Vert =B_2(e_1,e_2,e_f,{\eta }_{1d},{\dot{\eta }}_{1d},{\ddot{\eta }}_{1d}).\end{array}$(43) For any $B_0>0$ and $B_1>0$, the sets ${\mathrm{\Pi }}_0:\{({\eta }_{1d},{\dot{\eta }}_{1d},{\ddot{\eta }}_{1d}):{\eta }_{1d}^2+{\dot{\eta }}_{1d}^2+{\ddot{\eta }}_{1d}^2\le B_0\}$ and the sets ${\mathrm{\Pi }}_1:=\{{e_1}^2+{e_2}^2+e_f^2+{\displaystyle \frac{1}{{\mathrm{\Delta }}_2^{}}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}\le 2B_1\}}$ are compact in $R^3$ and $R^4$, respectively. ${\mathrm{\Pi }}_0\times {\mathrm{\Pi }}_1$ is also compact in $R^7$. Therefore, $\Vert B_2\Vert$ has a maximum $B_m$ on ${\mathrm{\Pi }}_0\times {\mathrm{\Pi }}_1$.

Then, (43(43) $\begin{array}{r}\Vert {\dot{e}}_f+\frac{e_f^{}}{{\chi }_1}\Vert =\Vert {\dot{\alpha }}_1\Vert =B_2(e_1,e_2,e_f,{\eta }_{1d},{\dot{\eta }}_{1d},{\ddot{\eta }}_{1d}).\end{array}$(43) ) can be expressed by (44) $\begin{array}{r}{e}_f^T{\dot{e}}_f\le -\frac{e_f^T{e}_f}{{\chi }_1}+e_f^T{B}_m\le -\frac{e_f^T{e}_f}{{\chi }_1}+\frac{e_f^T{e}_f}{2}+\frac{B_m^2}{2}.\end{array}$(44) From (15(15) $\begin{array}{r}{\alpha }_1=-K_1{e}_1+{\dot{\eta }}_{1d},\end{array}$(15) ), (22(22) $\begin{array}{r}{U}_1=-{\hat{W}}_{G_2}^T{\phi }_2\left({\mathrm{H}}_2\right)-K_2{e}_2+{\dot{\alpha }}_{1f},\end{array}$(22) ), (44(44) $\begin{array}{r}{e}_f^T{\dot{e}}_f\le -\frac{e_f^T{e}_f}{{\chi }_1}+e_f^T{B}_m\le -\frac{e_f^T{e}_f}{{\chi }_1}+\frac{e_f^T{e}_f}{2}+\frac{B_m^2}{2}.\end{array}$(44) ), (42(42) $\begin{array}{rl}{\dot{V}}_{pos}& =e_1^T(e_2+e_f+{\alpha }_1-{\dot{\eta }}_{1d})+e_2^T[W_{G_2}^{\ast T}{\phi }_2\left({\mathrm{H}}_2\right)\\ & +U_1+{\epsilon }_{G_2}-{\dot{\alpha }}_{1f}]+e_f^T{\dot{e}}_f-\frac{1}{{\mathrm{\Delta }}_2}{\tilde{W}}_{G_2}^T{\dot{\hat{W}}}_{G_2}.\end{array}$(42) ) can be written as (45) $\begin{array}{rl}{\dot{V}}_{pos}& \le e_1^T(e_2+e_f-K_1{e}_1)+e_2^T({\tilde{W}}_{G_2}^T{\phi }_2(H_2)+{\epsilon }_{G_2}\\ & -K_2{e}_2)-\frac{e_f^T{e}_f}{{\chi }_1}+\frac{e_f^T{e}_f}{2}+\frac{B_m^2}{2}\\ & -e_2^T{\tilde{W}}_{G_2}^T{\phi }_2(H_2)+a_2{\tilde{W}}_{G_2}^T{\hat{W}}_{G_2}.\end{array}$(45) Using the Young's inequality, we get (46) $\begin{array}{r}\{\begin{array}{l}{e}_1^T{e}_2\le {\displaystyle \frac{e_1^T{e}_1}{2}+{\displaystyle \frac{e_2^T{e}_2}{2},}}\\ e_1^T{e}_f\le {\displaystyle \frac{e_1^T{e}_1}{2}+{\displaystyle \frac{e_f^T{e}_f}{2},}}\\ e_2^T{\epsilon }_{G_2}\le {\displaystyle \frac{e_2^T{e}_2}{2}+{\displaystyle \frac{{\epsilon }_{G_2}^T{\epsilon }_{G_2}}{2},}}\\ a_2{\tilde{W}}_{G_2}^T{\hat{W}}_{G_2}^{}\le {\displaystyle \frac{a_2{\Vert W_{G_2}^{\ast }\Vert }^2}{2}-{\displaystyle \frac{a_2}{2}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}}}\end{array}\end{array}$(46) Then, (45(45) $\begin{array}{rl}{\dot{V}}_{pos}& \le e_1^T(e_2+e_f-K_1{e}_1)+e_2^T({\tilde{W}}_{G_2}^T{\phi }_2(H_2)+{\epsilon }_{G_2}\\ & -K_2{e}_2)-\frac{e_f^T{e}_f}{{\chi }_1}+\frac{e_f^T{e}_f}{2}+\frac{B_m^2}{2}\\ & -e_2^T{\tilde{W}}_{G_2}^T{\phi }_2(H_2)+a_2{\tilde{W}}_{G_2}^T{\hat{W}}_{G_2}.\end{array}$(45) ) is further expressed as (47) $\begin{array}{rl}{\dot{V}}_{pos}& \le -e_1^T(K_1-\frac{1}{2}I)e_1-e_2^T(K_2-I)e_2\\ & -e_f^T(\frac{1}{{\chi }_1}-1)I{e}_f-\frac{a_2}{2}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}\\ & +\frac{B_m^2}{2}+\frac{{\epsilon }_{G_2}^T{\epsilon }_{G_2}}{2}+\frac{a_2{\Vert W_{G_2}^{\ast }\Vert }^2}{2}.\end{array}$(47) Choose $K_1\ge {\displaystyle \frac{\vartheta +1}{2}I,K_2\ge \frac{\vartheta +2}{2}I,\frac{1}{{\chi }_1}\ge \frac{\vartheta +2}{2}I,a_2\ge \frac{\vartheta }{{\mathrm{\Delta }}_2^{}}}$, where ϑ a positive constant. Then (47(47) $\begin{array}{rl}{\dot{V}}_{pos}& \le -e_1^T(K_1-\frac{1}{2}I)e_1-e_2^T(K_2-I)e_2\\ & -e_f^T(\frac{1}{{\chi }_1}-1)I{e}_f-\frac{a_2}{2}{\tilde{W}}_{G_2}^T{\tilde{W}}_{G_2}\\ & +\frac{B_m^2}{2}+\frac{{\epsilon }_{G_2}^T{\epsilon }_{G_2}}{2}+\frac{a_2{\Vert W_{G_2}^{\ast }\Vert }^2}{2}.\end{array}$(47) ) can be reexpressed as (48) $\begin{array}{r}{\dot{V}}_{pos}\le -\vartheta V_{pos}+C,\end{array}$(48) where $C={\displaystyle \frac{B_m^2}{2}+\frac{{\epsilon }_{G_2}^T{\epsilon }_{G_2}}{2}+\frac{a_2{\Vert W_{G_2}^{\ast }\Vert }^2}{2}}$.

Equation (48(48) $\begin{array}{r}{\dot{V}}_{pos}\le -\vartheta V_{pos}+C,\end{array}$(48) ) means that $V_{pos}$ is bounded eventually. Thus, all signals of the position close-loop system are uniformly ultimately bounded. Moreover, we can obtain that $e_1\le \sqrt{2(V_{pos}(0)+{\displaystyle \frac{C}{\vartheta })}}$. Thus, increasing the value of ϑ, the tracking error $e_1$ can be as small as possible.

5.2. Boundedness of fuzzy parameter estimate error

Theorem 5.2

Consider the nonlinear QUAV attitude model (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ) satisfying Assumptions 2.1 and 2.2, the virtual control law (32(32) $\begin{array}{r}{\alpha }_2=-K_3{\overline{e}}_3,\end{array}$(32) ); the actual control law (37(37) $\begin{array}{r}{U}_3=M_3^{-1}\left(-{\hat{W}}_{G_4}^T{\phi }_4\left({\overline{\mathrm{H}}}_4\right)-K_4{\overline{e}}_4\right),\end{array}$(37) ), and the fuzzy parameter updating law (40(40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) ). Then, the parameter estimate errors are uniformly ultimately bounded.

Proof.

The fuzzy parameter updating law is updated only when an event occurs, and remaining unchanged until the next event-sampled occurs. Thus, the proof can be divided into two cases.

Case 1: During the flow interval $(t_k\le t<t_{k+1},k\in Z^{+})$.

Consider the following Lyapunov function: (49) $\begin{array}{r}{V}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}\right].\end{array}$(49) The time derivative of $V_{{\tilde{W}}_{G_4}}$ along with (40(40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) ) yields (50) $\begin{array}{r}{\dot{V}}_{{\tilde{W}}_{G_4}}=0.\end{array}$(50) It follows from (50(50) $\begin{array}{r}{\dot{V}}_{{\tilde{W}}_{G_4}}=0.\end{array}$(50) ) that ${\tilde{W}}_{G_4}$ remains as a constant during the flow interval. Moreover, the value of the initial parameter estimation is ${\hat{W}}_{G_4}\left(0\right)=0$ and $W_{G_4}^{\ast }$ is bounded. Then, ${\tilde{W}}_{G_4}^{}\left(0\right)$ is bounded.

Case 2: At the triggering instant $(t=t_k,k\in Z^{+})$.

According to (49(49) $\begin{array}{r}{V}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}\right].\end{array}$(49) ), the first difference of $V_{{\tilde{W}}_{G_4}}$ is given by (51) $\begin{array}{r}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^{+T}{\tilde{W}}_{G_4}^{+}\right]-tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}\right]\end{array}$(51) Define ${\tilde{W}}_{G_4}^{+}=W_{G_4}^{\ast }-{\hat{W}}_{G_4}^{+}$, $\mathrm{\Delta }{\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-{\hat{W}}_{G_4}^{+}$. Then, from (40), we have (52) $\begin{array}{r}\{\begin{array}{l}{\tilde{W}}_{G_4}^{+}=\mathrm{\Delta }{\hat{W}}_{G_4}^{+}+{\tilde{W}}_{G_4},\\ \mathrm{\Delta }{\hat{W}}_{G_4}^{+}=b_4{\displaystyle \frac{s_4^{}}{c_4+s_4^T{s}_4^{}}{\phi }_4\left({\mathrm{H}}_4\right)+{\kappa }_4{\hat{W}}_{G_4}.}\end{array}\end{array}$(52) Considering (51(51) $\begin{array}{r}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^{+T}{\tilde{W}}_{G_4}^{+}\right]-tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}\right]\end{array}$(51) ) and (52(52) $\begin{array}{r}\{\begin{array}{l}{\tilde{W}}_{G_4}^{+}=\mathrm{\Delta }{\hat{W}}_{G_4}^{+}+{\tilde{W}}_{G_4},\\ \mathrm{\Delta }{\hat{W}}_{G_4}^{+}=b_4{\displaystyle \frac{s_4^{}}{c_4+s_4^T{s}_4^{}}{\phi }_4\left({\mathrm{H}}_4\right)+{\kappa }_4{\hat{W}}_{G_4}.}\end{array}\end{array}$(52) ), then substituting ${\tilde{W}}_{G_4}=W_{G_4}^{\ast }-{\hat{W}}_{G_4}$ yields (53) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}& =tr\{{\left[{\tilde{W}}_{G_4}+{\mathrm{b}}_4{\lambda }_4{\phi }_4\left({\mathrm{H}}_4\right)+{\kappa }_4{\hat{W}}_{G_4}^{}\right]}^T\\ & \times \left[{\tilde{W}}_{G_4}^{}+{\mathrm{b}}_4{\lambda }_4{\phi }_4\left({\mathrm{H}}_4\right)+{\kappa }_4{\hat{W}}_{G_4}^{}\right]\}\\ & -tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}\right],\\ & =b_4^2{\lambda }_4^{2}tr[{\phi }_4^T\left({\mathrm{H}}_4\right){\phi }_4\left({\mathrm{H}}_4\right)]\\ & +{\kappa }_4^{2}tr\left[{\left(W_{G_4}^{\ast }-{\tilde{W}}_{G_4}^{}\right)}^T\left(W_{G_4}^{\ast }-{\tilde{W}}_{G_4}^{}\right)\right]\\ & +2b_4{\lambda }_{4}tr[{\tilde{W}}_{G_4}^T{\phi }_4\left({\mathrm{H}}_4\right)]\\ & +2{\kappa }_{4}tr\left[{\tilde{W}}_{G_4}^T{W}_{G_4}^{\ast }\right]-2{\kappa }_{4}tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}^{}\right]\\ & +2b_4{\lambda }_4{\kappa }_{4}tr[{\phi }_4^T\left({\mathrm{H}}_4\right)W_{G_4}^{\ast }]\\ & -2b_4{\lambda }_4{\kappa }_{4}tr[{\phi }_4^T\left({\mathrm{H}}_4\right){\tilde{W}}_{G_4}^{}],\end{array}$(53) where ${\lambda }_4=s_4/(c_4+s_4^T{s}_4)$.

Using the Young's inequality, we have (54) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}^{}}& \le b_4^2{\lambda }_4^T{\lambda }_4^{}{\phi }_{4m}^2+2{\kappa }_4^2{\Vert W_{G_4}^{\ast }\Vert }^2+2{\kappa }_4^2{\Vert {\tilde{W}}_{G_4}\Vert }^2\\ & +2b_4{\phi }_{4m}^{}\Vert {\lambda }_4\Vert \Vert {\tilde{W}}_{G_4}\Vert \\ & +2{\kappa }_4\Vert {\tilde{W}}_{G_4}^{}\Vert \Vert W_{G_4}^{\ast }\Vert -2{\kappa }_4{\Vert {\tilde{W}}_{G_4}\Vert }^2\\ & +2b_4{\kappa }_4{\phi }_{4m}^{}\Vert {\lambda }_4\Vert \Vert W_{G_4}^{\ast }\Vert \\ & +2b_4{\kappa }_4{\phi }_{4m}\Vert {\lambda }_4\Vert \Vert {\tilde{W}}_{G_4}\Vert ,\end{array}$(54) where ${\phi }_{4m}$ is the boundary of ${\phi }_4$.

Choose a positive parameter $c_4$ satisfing $0\le \Vert {\lambda }_4^{}\Vert <1$. Then (54) can be written as (55) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}^{}}& \le b_4^2{\phi }_{4m}^2+2{\kappa }_4^2{\Vert W_{G_4}^{\ast }\Vert }^2+2{\kappa }_4^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\\ & +2b_4{\phi }_{4m}^{}\Vert {\tilde{W}}_{G_4}^{}\Vert +2{\kappa }_4\Vert {\tilde{W}}_{G_4}^{}\Vert \Vert W_{G_4}^{\ast }\Vert \\ & -2{\kappa }_4{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+2b_4{\kappa }_4{\phi }_{4m}^{}\Vert W_{G_4}^{\ast }\Vert \\ & +2b_4{\kappa }_4{\phi }_{4m}^{}\Vert {\tilde{W}}_{G_4}^{}\Vert ,\\ & \le 2b_4{\phi }_{4m}^{}\left(1+{\kappa }_4\right)\Vert {\tilde{W}}_{G_4}^{}\Vert \\ & -\left({\kappa }_4-2{\kappa }_4^2\right){\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+{\zeta }_4,\end{array}$(55) where ${\zeta }_4=b_4^2{\phi }_{4m}^2+\left({\kappa }_4+2{\kappa }_4^2\right){\Vert W_{G_{4m}}^{}\Vert }^2+2b_4{\kappa }_4{\phi }_{4m}^{}{W}_{G_{4m}}^{}$.

Let $l_{14}={\kappa }_4-2{\kappa }_4^2>0$, namely $0<{\kappa }_4<1/2$, and $l_{24}=2b_4{\phi }_{4m}^{}\left(1+{\kappa }_4\right)>0$, Then (55(55) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}^{}}& \le b_4^2{\phi }_{4m}^2+2{\kappa }_4^2{\Vert W_{G_4}^{\ast }\Vert }^2+2{\kappa }_4^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\\ & +2b_4{\phi }_{4m}^{}\Vert {\tilde{W}}_{G_4}^{}\Vert +2{\kappa }_4\Vert {\tilde{W}}_{G_4}^{}\Vert \Vert W_{G_4}^{\ast }\Vert \\ & -2{\kappa }_4{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+2b_4{\kappa }_4{\phi }_{4m}^{}\Vert W_{G_4}^{\ast }\Vert \\ & +2b_4{\kappa }_4{\phi }_{4m}^{}\Vert {\tilde{W}}_{G_4}^{}\Vert ,\\ & \le 2b_4{\phi }_{4m}^{}\left(1+{\kappa }_4\right)\Vert {\tilde{W}}_{G_4}^{}\Vert \\ & -\left({\kappa }_4-2{\kappa }_4^2\right){\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+{\zeta }_4,\end{array}$(55) ) can be further expressed as (56) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}& \le l_{24}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\\ & +{\zeta }_4\le \frac{1}{l_{14}}\left(l_{24}{l}_{14}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\right)+{\zeta }_4,\\ & \le \frac{1}{l_{14}}\left(\frac{l_{24}^2}{2}-\frac{l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}\right)\\ & +{\zeta }_4\le \frac{l_{24}^2}{2l_{14}}-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\zeta }_4,\\ & =-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\overline{\zeta }}_4,\end{array}$(56) where ${\overline{\zeta }}_4=l_{24}^2/2l_{14}+{\zeta }_4$.

It follows from (56(56) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}& \le l_{24}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\\ & +{\zeta }_4\le \frac{1}{l_{14}}\left(l_{24}{l}_{14}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\right)+{\zeta }_4,\\ & \le \frac{1}{l_{14}}\left(\frac{l_{24}^2}{2}-\frac{l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}\right)\\ & +{\zeta }_4\le \frac{l_{24}^2}{2l_{14}}-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\zeta }_4,\\ & =-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\overline{\zeta }}_4,\end{array}$(56) ) that $\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}<0$ as long as $\Vert {\tilde{W}}_{G_4}^{}\Vert >\sqrt{2{\overline{\zeta }}_4/l_{14}}$. Thus, ${\tilde{W}}_{G_4}$ is uniformly ultimately bounded.

From the above two cases, the fuzzy parameter estimate error ${\tilde{W}}_{G_4}$ remains as a constant during the flow interval, and bounded at the triggering instants. Therefore, ${\tilde{W}}_{G_4}$ is uniformly ultimately bounded.

5.3. Attitude closed-loop system stability

Theorem 5.3

Consider the nonlinear QUAV attitude model (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ) satisfying Assumptions 2.1 and 2.2, the virtual control law (32(32) $\begin{array}{r}{\alpha }_2=-K_3{\overline{e}}_3,\end{array}$(32) ), the actual control law (37(37) $\begin{array}{r}{U}_3=M_3^{-1}\left(-{\hat{W}}_{G_4}^T{\phi }_4\left({\overline{\mathrm{H}}}_4\right)-K_4{\overline{e}}_4\right),\end{array}$(37) ), and the fuzzy parameter updating law (40(40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) ). Then, for any bounded initial conditions, all signals of the closed-loop attitude systems are uniformly bounded, and the attitude tracking error converges to the neighbourhood of zero.

Proof.

The proof can be divided into two cases.

Case 1: During the flow interval $(t_k\le t<t_{k+1},k\in Z^{+})$.

Consider the following Lyapunov function: (57) $\begin{array}{r}V=V_e+V_{\overline{e}}+V_{{\tilde{W}}_{G_4}^{}},\end{array}$(57) where (58) $\{\begin{array}{rl}{V}_e=& {\displaystyle \frac{1}{2}\sum _{i=3}^4{\mathrm{e}}_i^T{\mathrm{e}}_i,}\\ V_{\overline{e}}=& {\displaystyle \frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^T{\overline{e}}_i,}\\ V_{{\tilde{W}}_{G_4}^{}}=& tr\left[{\tilde{W}}_{G_4}^T{\tilde{W}}_{G_4}^{}\right].\end{array}$(58)  The time derivative of $V_e$ along (34(34) $\begin{array}{r}{\dot{e}}_3=e_4+K_3{s}_3-K_3{e}_3+{\dot{\eta }}_{3d}+K_3({\eta }_{3d}-{\eta }_{3d}(t_k)),\end{array}$(34) ) and (39(39) $\begin{array}{rl}{\dot{e}}_4& =K_4{s}_4-K_4{e}_4\\ & +{\hat{W}}_{G_4}^T\left[{\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\right]+{\tilde{W}}_{G_4}^{{}^T}{\phi }_4\left({\mathrm{H}}_4\right)+{\epsilon }_{G_4},\end{array}$(39) ) can be written as (59) $\begin{array}{rl}{\dot{V}}_e& =-\sum _{i=3}^4{e}_i^T{K}_i{e}_i+e_3^T{K}_3{s}_3\\ & +e_4^T\{K_4{s}_4+{\hat{W}}_{G_4}^T\left[{\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\right]\}+e_3^T{\dot{\eta }}_{3d}\\ & +e_3^T{K}_3({\eta }_{3d}-{\eta }_{3d}(t_k))+e_3^T{e}_4+e_4^T[{\tilde{W}}_{G_4}^{{}^T}{\phi }_4\left({\mathrm{H}}_4\right)+{\epsilon }_{G_4}^{}]\end{array}$(59) Let $S_4={\mathrm{H}}_4-{\overline{\mathrm{H}}}_4={\left[s_3,s_4,s_{cs}\right]}^T$. From $0<{\phi }^T(\cdot )\phi (\cdot )<1$ and Assumption 2.2, we have 60 $\{\begin{array}{rl}& {\mathrm{e}}_4^T{\tilde{W}}_{G_4}^T{\phi }_4\left({\mathrm{H}}_4\right)\le {\displaystyle \frac{1}{4}{\mathrm{e}}_4^T{e}_4+{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2,}\\ & {\mathrm{e}}_4^T{\epsilon }_{G_4}^{}\le {\displaystyle \frac{1}{4}{\mathrm{e}}_4^T{e}_4+{\delta }_{G_4}^2,}\\ & {\mathrm{e}}_3^T{\dot{\eta }}_{3d}\le {\displaystyle \frac{1}{2}{\mathrm{e}}_3^T{e}_3+{\displaystyle \frac{1}{2}{\eta }_{3dm}^2,}}\\ & {\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\le L_4{S}_4.\end{array}$60 From (59(59) $\begin{array}{rl}{\dot{V}}_e& =-\sum _{i=3}^4{e}_i^T{K}_i{e}_i+e_3^T{K}_3{s}_3\\ & +e_4^T\{K_4{s}_4+{\hat{W}}_{G_4}^T\left[{\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\right]\}+e_3^T{\dot{\eta }}_{3d}\\ & +e_3^T{K}_3({\eta }_{3d}-{\eta }_{3d}(t_k))+e_3^T{e}_4+e_4^T[{\tilde{W}}_{G_4}^{{}^T}{\phi }_4\left({\mathrm{H}}_4\right)+{\epsilon }_{G_4}^{}]\end{array}$(59) ) and (6060 $\{\begin{array}{rl}& {\mathrm{e}}_4^T{\tilde{W}}_{G_4}^T{\phi }_4\left({\mathrm{H}}_4\right)\le {\displaystyle \frac{1}{4}{\mathrm{e}}_4^T{e}_4+{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2,}\\ & {\mathrm{e}}_4^T{\epsilon }_{G_4}^{}\le {\displaystyle \frac{1}{4}{\mathrm{e}}_4^T{e}_4+{\delta }_{G_4}^2,}\\ & {\mathrm{e}}_3^T{\dot{\eta }}_{3d}\le {\displaystyle \frac{1}{2}{\mathrm{e}}_3^T{e}_3+{\displaystyle \frac{1}{2}{\eta }_{3dm}^2,}}\\ & {\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\le L_4{S}_4.\end{array}$60 ), we obtain 61 $\begin{array}{rl}{\dot{V}}_e& \le -\sum _{i=3}^4{\mathrm{e}}_i^T\left({\mathrm{K}}_i-I\right){\mathrm{e}}_i+2\Vert {\mathrm{e}}_3^{}\Vert \Vert {\mathrm{K}}_3\Vert \Vert {\mathrm{s}}_3\Vert \\ & +\Vert e_4\Vert (\Vert K_4\Vert \Vert s_4\Vert +\Vert {\hat{W}}_{G_4}^{}\Vert L_4\Vert S_4\Vert )\\ & +{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+{\delta }_{G_4}^2+{\eta }_{3dm}^2.\end{array}$61 An adaptive event-triggered condition is designed as (62) $\Vert s{s}_i\Vert \le {\sigma }_i\Vert e_i\Vert ,$(62) where $s{s}_i=[\underset{-}{s_1},\dots ,\underset{-}{s_i}{]}^T$, $\underset{-}{s_3}\text{ = }{s}_3$, $\underset{-}{s_4}\text{ = [}{s}_3,s_4{\text{,s}}_{cs}^{}{\text{]}}^T$, ${\sigma }_3={\mathrm{\Gamma }}_3/(2\Vert K_3\Vert )$, ${\sigma }_4={\mathrm{\Gamma }}_4/\left(\Vert K_4\Vert +\Vert {\hat{W}}_{G_4}\Vert L_4\right)$.

The event-triggered condition can be expressed as (63) $\Vert ss\Vert \le \sigma \Vert e\Vert ,$(63) where $ss=[s{s}_3,s{s}_4{]}^T$, $e={\left[e_3,e_4\right]}^T$, $\sigma =\sqrt{{\sigma }_3^2+{\sigma }_4^2}$.

Substituting (62(62) $\Vert s{s}_i\Vert \le {\sigma }_i\Vert e_i\Vert ,$(62) ) into (6161 $\begin{array}{rl}{\dot{V}}_e& \le -\sum _{i=3}^4{\mathrm{e}}_i^T\left({\mathrm{K}}_i-I\right){\mathrm{e}}_i+2\Vert {\mathrm{e}}_3^{}\Vert \Vert {\mathrm{K}}_3\Vert \Vert {\mathrm{s}}_3\Vert \\ & +\Vert e_4\Vert (\Vert K_4\Vert \Vert s_4\Vert +\Vert {\hat{W}}_{G_4}^{}\Vert L_4\Vert S_4\Vert )\\ & +{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+{\delta }_{G_4}^2+{\eta }_{3dm}^2.\end{array}$61 ) yields (64) $\begin{array}{rl}{\dot{V}}_e\le & -\sum _{i=3}^4{\mathrm{e}}_i^T\left({\mathrm{K}}_i-I\right){\mathrm{e}}_i+2{\sigma }_3\Vert {\mathrm{K}}_3\Vert {\Vert {\mathrm{e}}_3^{}\Vert }^2\\ & ++{\sigma }_4{\Vert e_4\Vert }^2(\Vert K_4\Vert +\Vert {\hat{W}}_{G_4}^{}\Vert L_4)+\gamma \end{array}$(64) where $\gamma ={\Vert {\tilde{W}}_{G_4}^{}\Vert }^2+{\delta }_{G_4}^2+{\eta }_{3dm}^2>0$.

Then, (64(64) $\begin{array}{rl}{\dot{V}}_e\le & -\sum _{i=3}^4{\mathrm{e}}_i^T\left({\mathrm{K}}_i-I\right){\mathrm{e}}_i+2{\sigma }_3\Vert {\mathrm{K}}_3\Vert {\Vert {\mathrm{e}}_3^{}\Vert }^2\\ & ++{\sigma }_4{\Vert e_4\Vert }^2(\Vert K_4\Vert +\Vert {\hat{W}}_{G_4}^{}\Vert L_4)+\gamma \end{array}$(64) ) can be further expressed as (65) ${\dot{V}}_e\le -\sum _{i=3}^4{\mathrm{e}}_i^T\left[{\mathrm{K}}_i-\left(1+{\mathrm{\Gamma }}_i\right)I\right]{\mathrm{e}}_i+\gamma .$(65) The time derivative of $V_{\overline{e}}$ along (33(33) $\begin{array}{r}{\dot{\overline{e}}}_3=0\end{array}$(33) ) and (38(38) $\begin{array}{r}{\dot{\overline{e}}}_4=0.\end{array}$(38) ) can be described by (66) ${\dot{V}}_{\overline{e}}=\sum _{i=3}^4{\overline{e}}_i^T{\dot{\overline{e}}}_i=0.$(66) Considering $V_{{\tilde{W}}_{G_4}}$ and the first equation in (40(40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) ), we obtain (67) ${\dot{V}}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^T{\dot{\tilde{W}}}_{G_4}\right]=0.$(67) The derivative of V along (65(65) ${\dot{V}}_e\le -\sum _{i=3}^4{\mathrm{e}}_i^T\left[{\mathrm{K}}_i-\left(1+{\mathrm{\Gamma }}_i\right)I\right]{\mathrm{e}}_i+\gamma .$(65) )–(67(67) ${\dot{V}}_{{\tilde{W}}_{G_4}}=tr\left[{\tilde{W}}_{G_4}^T{\dot{\tilde{W}}}_{G_4}\right]=0.$(67) ) becomes (68) $\dot{V}\le -\sum _{i=3}^4{\mathrm{e}}_i^T\left[{\mathrm{K}}_i-\left(1+{\mathrm{\Gamma }}_i\right)I\right]{\mathrm{e}}_i+\gamma \le -N_e\sum _{i=3}^4{\Vert e_i\Vert }^2+\gamma ,$(68) where $N_e=min\{{\lambda }_{min}\left[{\mathrm{K}}_i-\left(1+{\mathrm{\Gamma }}_i\right)\mathrm{I}\right]\}$ and ${\lambda }_{min}(\cdot )$ is the minimum eigenvalue of the matrix. Choose positive matrixs $K_i$, such that (69) ${\lambda }_{min}({\mathrm{K}}_i)>1+{\mathrm{\Gamma }}_i.$(69) Then, it follows from (68(68) $\dot{V}\le -\sum _{i=3}^4{\mathrm{e}}_i^T\left[{\mathrm{K}}_i-\left(1+{\mathrm{\Gamma }}_i\right)I\right]{\mathrm{e}}_i+\gamma \le -N_e\sum _{i=3}^4{\Vert e_i\Vert }^2+\gamma ,$(68) ) that $\dot{V}<0$ as long as $\Vert e_i\Vert >\sqrt{\gamma /N_e}$. Therefore, $\Vert e_i\Vert <\sqrt{\gamma /N_e}\stackrel{\mathrm{\Delta }}{=}{\mathrm{D}}_1^e$, namely $e_i$ is bounded. During the flow interval $(t_k\le t<t_{(t_k\le t<t_{k+1},k\in Z^{+})k+1},k\in Z^{+})$, both ${\tilde{W}}_{G_4}$ and ${\overline{e}}_i$ are constants, it can be derived that ${\tilde{W}}_{G_4}$ and ${\overline{e}}_i$ are bounded.

Case 2: At the triggering instant $(t=t_k,k\in Z^{+})$.

The first difference of (57(57) $\begin{array}{r}V=V_e+V_{\overline{e}}+V_{{\tilde{W}}_{G_4}^{}},\end{array}$(57) ) yields (70) $\mathrm{\Delta }V=\mathrm{\Delta }{V}_e+\mathrm{\Delta }{V}_{\overline{e}}+\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}.$(70) Let state vectors ${\eta }_i^{+}={\eta }_i$ when the event-sampled occurs $(t=t_k)$. According to (30(30) $\begin{array}{r}{e}_3={\eta }_3-{\eta }_{3d},\end{array}$(30) ) and (35(35) $\begin{array}{r}{e}_4={\eta }_4-{\alpha }_2.\end{array}$(35) ), we have (71) $\{\begin{array}{rl}\mathrm{\Delta }{e}_i^{}=& e_i^{+}-e_i^{}=0,\\ \mathrm{\Delta }{\overline{e}}_i^{}=& {\overline{e}}_i^{+}-{\overline{e}}_i=e_i-{\overline{e}}_i^{}=s_i.\end{array}$(71) Substituting (71(71) $\{\begin{array}{rl}\mathrm{\Delta }{e}_i^{}=& e_i^{+}-e_i^{}=0,\\ \mathrm{\Delta }{\overline{e}}_i^{}=& {\overline{e}}_i^{+}-{\overline{e}}_i=e_i-{\overline{e}}_i^{}=s_i.\end{array}$(71) ) into (70(70) $\mathrm{\Delta }V=\mathrm{\Delta }{V}_e+\mathrm{\Delta }{V}_{\overline{e}}+\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}.$(70) ) yields (72) $\mathrm{\Delta }{V}_e=\frac{1}{2}\sum _{i=1}^4{e}_i^2\left(t^{+}\right)-\frac{1}{2}\sum _{i=1}^4{e}_i^2\left(t\right)=0.$(72) (73) $\begin{array}{rl}\mathrm{\Delta }{V}_{\overline{e}}& =\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t^{+}\right)-\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)\\ & =\frac{1}{2}\sum _{i=3}^4{e}_i^2\left(t\right)-\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)\le -\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)+D_1,\end{array}$(73) where ${\mathrm{D}}_1=\frac{1}{2}{\left({\mathrm{D}}_1^e\right)}^2$.

Considering (56(56) $\begin{array}{rl}\mathrm{\Delta }{V}_{{\tilde{W}}_{G_4}}& \le l_{24}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\\ & +{\zeta }_4\le \frac{1}{l_{14}}\left(l_{24}{l}_{14}\Vert {\tilde{W}}_{G_4}^{}\Vert -l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2\right)+{\zeta }_4,\\ & \le \frac{1}{l_{14}}\left(\frac{l_{24}^2}{2}-\frac{l_{14}^2{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}\right)\\ & +{\zeta }_4\le \frac{l_{24}^2}{2l_{14}}-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\zeta }_4,\\ & =-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+{\overline{\zeta }}_4,\end{array}$(56) ), (72(72) $\mathrm{\Delta }{V}_e=\frac{1}{2}\sum _{i=1}^4{e}_i^2\left(t^{+}\right)-\frac{1}{2}\sum _{i=1}^4{e}_i^2\left(t\right)=0.$(72) ) and (73(73) $\begin{array}{rl}\mathrm{\Delta }{V}_{\overline{e}}& =\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t^{+}\right)-\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)\\ & =\frac{1}{2}\sum _{i=3}^4{e}_i^2\left(t\right)-\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)\le -\frac{1}{2}\sum _{i=3}^4{\overline{e}}_i^2\left(t\right)+D_1,\end{array}$(73) ), we obtain (74) $\begin{array}{r}\mathrm{\Delta }V\le -\frac{1}{2}\sum _{i=3}^4{\Vert {\overline{e}}_i^{}\left(t\right)\Vert }^2-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+D,\end{array}$(74) where $D=D_1+{\overline{\zeta }}_4$.

From (74(74) $\begin{array}{r}\mathrm{\Delta }V\le -\frac{1}{2}\sum _{i=3}^4{\Vert {\overline{e}}_i^{}\left(t\right)\Vert }^2-\frac{l_{14}^{}{\Vert {\tilde{W}}_{G_4}^{}\Vert }^2}{2}+D,\end{array}$(74) ), we get $\mathrm{\Delta }V<0$ as long as $\Vert {\overline{e}}_i\Vert >\sqrt{2D}$ and $\Vert {\tilde{W}}_{G_4}^{}\Vert >\sqrt{2D/l_{14}}$. Therefore, $\Vert {\overline{e}}_i\Vert <\sqrt{2D}\stackrel{\mathrm{\Delta }}{=}{\mathrm{D}}_1^{\overline{e}}$ and $\Vert {\tilde{W}}_{G_4}^{}\Vert <\sqrt{2D/l_{14}}\stackrel{\mathrm{\Delta }}{=}{\mathrm{D}}_2^{{\tilde{W}}_{G_4}^{}}$ at the triggering instant $(t=t_k,k\in Z^{+})$.

From the above two cases, it is proved that all signals of the attitude closed-loop systems are uniformly and ultimately bounded, and the attitude tracking error can converge to the neighbourhood of zero by properly selecting the design parameters.

Remark 5.1

To improve the resource utilization, an event-triggered trajectory tracking algorithm is presented. The spirit of the presented algorithm is that the controller in the attitude subsystem is updated in a aperiodic form, and the triggered instants are determined by the event-triggered condition (63(63) $\Vert ss\Vert \le \sigma \Vert e\Vert ,$(63) ) related to the measurement errors (24(24) $\begin{array}{r}{s}_i\left(t\right)={\eta }_i\left(t\right)-{\overline{\eta }}_i\left(t\right),i=3,4\end{array}$(24) ) and (25(25) $\begin{array}{r}{s}_{cs}\left(t\right)=d_3\left(t\right)-{\overline{d}}_3\left(t\right).\end{array}$(25) ). If the event-trigger condition is violated, the measurement error exceeds a certain threshold, and the current attitude controller should be updated and transmitted; otherwise, the attitude controller remains unchange.

5.4. Minimum interevent time

Theorem 5.4

Consider the nonlinear QUAV attitude model (5(5) $\begin{array}{r}\{\begin{array}{l}{\dot{\eta }}_3={\eta }_4\\ {\dot{\eta }}_4=G_4\left({\eta }_3,{\eta }_4,t\right)+M_3{U}_3\end{array}\end{array}$(5) ), the virtual control law (32(32) $\begin{array}{r}{\alpha }_2=-K_3{\overline{e}}_3,\end{array}$(32) ), the actual control law (37(37) $\begin{array}{r}{U}_3=M_3^{-1}\left(-{\hat{W}}_{G_4}^T{\phi }_4\left({\overline{\mathrm{H}}}_4\right)-K_4{\overline{e}}_4\right),\end{array}$(37) ), and the fuzzy parameter updating law (40(40) $\begin{array}{r}\{\begin{array}{l}{\dot{\hat{W}}}_{G_4}=0,t_k\le t<t_{k+1}\\ {\hat{W}}_{G_4}^{+}={\hat{W}}_{G_4}-b_4\frac{{\displaystyle s_4}}{{\displaystyle c_4+s_4^T{s}_4^{}}}{\phi }_4\left({\mathrm{H}}_4\right)-{\kappa }_4{\hat{W}}_{G_4},t=t_k\end{array}\end{array}$(40) ) by the violation of event-triggered condition (63(63) $\Vert ss\Vert \le \sigma \Vert e\Vert ,$(63) ). Suppose Assumptions 2.1 to 2.2 hold. Then, the event-triggered minimum intersample time T is lower bounded by a nonzero positive constant. Namely, Zeno behaviour is completely excluded.

Proof.

Recalling the error dynamics (34(34) $\begin{array}{r}{\dot{e}}_3=e_4+K_3{s}_3-K_3{e}_3+{\dot{\eta }}_{3d}+K_3({\eta }_{3d}-{\eta }_{3d}(t_k)),\end{array}$(34) ) and (39(39) $\begin{array}{rl}{\dot{e}}_4& =K_4{s}_4-K_4{e}_4\\ & +{\hat{W}}_{G_4}^T\left[{\phi }_4\left({\mathrm{H}}_4\right)-{\phi }_4\left({\overline{\mathrm{H}}}_4\right)\right]+{\tilde{W}}_{G_4}^{{}^T}{\phi }_4\left({\mathrm{H}}_4\right)+{\epsilon }_{G_4},\end{array}$(39) ) for $(t_k\le t<t_{k+1},k\in Z^{+})$, it can be rewritten in the following form: (75) $\dot{e}=Ae+P$(75) where $\begin{array}{r}A=\left[\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 0& 0\end{array}\right],P=\left[\begin{array}{c}{f}_3\\ \begin{array}{l}{f}_4,\end{array}\end{array}\right]\end{array}$ $f_3$ and $f_4$ are nonlinear functions satisfying the following inequality (76) $\begin{array}{r}\{\begin{array}{l}\Vert f_3\Vert \le \Vert K_3\Vert \Vert {\overline{e}}_3\Vert ,\\ \Vert f_4\Vert \le \Vert K_4\Vert \Vert {\overline{e}}_4\Vert +2L_4{\phi }_{4m}\Vert {\hat{W}}_{G_4}^{}\Vert +{\phi }_{4m}\Vert {\tilde{W}}_{G_4}^{}\Vert +{\delta }_{G_4}.\end{array}\end{array}$(76) It follows from (75(75) $\dot{e}=Ae+P$(75) ) that (77) $\Vert \underset{-}{{\dot{e}}_i}\Vert ⩽\Vert A_i\Vert \Vert \underset{-}{e_i}\Vert +P_m,$(77) where $\underset{-}{e_i}={\left[e_1,\dots ,e_i\right]}^T$. $P_m=\underset{t_k\le t<t_{k+1}}{max}||f_i||(i=3,4)$.

Notice that (78) $\frac{d}{dt}\underset{-}{e_i}⩽\frac{d}{dt}{\left({\underset{-}{e_i}}^2\right)}^{1/2}⩽\frac{\Vert \underset{-}{e_i}\underset{-}{{\dot{e}}_i}\Vert }{\Vert \underset{-}{e_i}\Vert }⩽\Vert \underset{-}{{\dot{e}}_i}\Vert =\Vert \underset{-}{{\dot{s}}_i}\Vert .$(78) From (77(77) $\Vert \underset{-}{{\dot{e}}_i}\Vert ⩽\Vert A_i\Vert \Vert \underset{-}{e_i}\Vert +P_m,$(77) ) and (78(78) $\frac{d}{dt}\underset{-}{e_i}⩽\frac{d}{dt}{\left({\underset{-}{e_i}}^2\right)}^{1/2}⩽\frac{\Vert \underset{-}{e_i}\underset{-}{{\dot{e}}_i}\Vert }{\Vert \underset{-}{e_i}\Vert }⩽\Vert \underset{-}{{\dot{e}}_i}\Vert =\Vert \underset{-}{{\dot{s}}_i}\Vert .$(78) ), under the initial condition $\underset{-}{s_i}\left(t^{+}\right)=0$ for $t\text{ = }{t}_k$, we can obtain the solution of the above inequality for $(t_k\le t<t_{k+1},k\in Z^{+})$ (79) $\begin{array}{rl}\Vert \underset{-}{s_i}\Vert & ⩽{\int }_{t_k^{+}}^t\Vert P_m\Vert \exp \left(\Vert A_i\Vert \left(t-x\right)\right)dt,\\ & ⩽\frac{\Vert P_m\Vert }{\Vert A_i\Vert }\left[\exp \left(\Vert A_i\Vert \left(t-t_k\right)\right)-1\right],\\ & ⩽\frac{\Vert P_m\Vert }{\Vert A_i\Vert }\left[\exp \left(\Vert A_i\Vert \left(t_{k+1}-t_k\right)\right)-1\right].\end{array}$(79) According to the event-triggered condition and the errors boundary, we have (80) ${\sigma }_i{\mathrm{D}}_1^e\le \frac{\Vert P_m\Vert }{\Vert A_i\Vert }\left[\exp \left(\Vert A_i\Vert \left(t_{k+1}-t_k\right)\right)-1\right].$(80) Then, the event-triggered minimum intersample time T can be expressed as (81) $T=t_{k+1}-t_k=\frac{1}{\Vert A_i\Vert }\ln \left(\frac{\Vert A_i\Vert }{P_m}{\sigma }_i{\mathrm{D}}_1^e+1\right)>0.$(81) It follows from (81(81) $T=t_{k+1}-t_k=\frac{1}{\Vert A_i\Vert }\ln \left(\frac{\Vert A_i\Vert }{P_m}{\sigma }_i{\mathrm{D}}_1^e+1\right)>0.$(81) ) that during the event-triggered interevent time $(t_k\le t<t_{k+1},k\in Z^{+})$, the minimum intersample time T is bounded away from zero, namely, the Zeno phenomenon can be completely excluded.

6. Simulation studies

In this section, the effectiveness of the proposed adaptive fuzzy controller is demonstrated through the QUAV system. The system parameters of the QUAV with nonlinear external disturbances are shown in Table 1.

Table 1. The parameter value of the QUAV.

The parameter	The value
m	$1.2kg$
l	$0.2m$
g	$9.8m/s^2$
$k_f$	${10}^{-6}N(m/s{)}^{-2}$
$I_{xx}$	$0.015Nm{\cdot }^2/rad$
$I_{yy}$	$0.015Nm{\cdot }^2/rad$
$I_{zz}$	$0.026Nm{\cdot }^2/rad$

The nonlinear external disturbance is set as $d_q=0.2\sin ({\eta }_q+{\eta }_{q+1})+0.5[\cos t,\sin t,\cos t{]}^T(q=1,3)$. The desire trajectory and the desire yaw angle are chosen as ${\eta }_{1d}={\left[-2\sin t,3\cos t,3{\sin }^{2}t+1\right]}^T$ and ${\psi }_d=\sin t$, respectively. In simulation, the initial values of position vector and velocity vector are set as $[{\eta }_1(0),{\eta }_2(0){]}^T={\left[-0.2,0.2,0.2,0,0,0\right]}^T$. The initial values of Euler angle vector and the angular velocity vector are set as $[{\eta }_3(0),{\eta }_4(0){]}^T={\left[0.1,0,0,0,0,0\right]}^T$.

The controller parameters are chosen as ${\mathrm{K}}_1=\{21,21,21\}{\mathrm{K}}_1=\{21,21,21\}$, $diag$, ${\mathrm{K}}_4=\{15,15,15\}{\mathrm{K}}_4=\{15,15,15\}$;  ${\mathrm{\Delta }}_2=30$, $a_2=0.01$, ${\chi }_1=0.005$,  $b_{41}=1.5$, $b_{42}=0.5$, $b_{43}=1$,  ${\kappa }_{41}=0.02$, ${\kappa }_{42}={\kappa }_{43}=0.03$,  $c_{41}=1.2$, $c_{42}=0.06$, $c_{43}=0.06$,  ${\mathrm{\Gamma }}_3={\mathrm{\Gamma }}_4=6$,  $L_4=1$.

Fuzzy membership functions are chosen as

$\{\begin{array}{l}\mu ({\eta }_1)=exp[-\frac{{({\eta }_{11}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{12}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{13}\pm k)}^2}{4}],\\ \mu ({\eta }_2)=exp[-\frac{{({\eta }_{21}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{22}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{23}\pm k)}^2}{4}],\\ \mu ({\eta }_3)=exp[-\frac{{({\eta }_{31}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{32}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{33}\pm k)}^2}{4}],\\ \mu ({\eta }_4)=exp[-\frac{{({\eta }_{41}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{42}\pm k)}^2}{4}]\ast exp[-\frac{{({\eta }_{43}\pm k)}^2}{4}],k=0,1,2.\end{array}$The simulation time is set as $10s$, and the sampling time is $0.001s$. 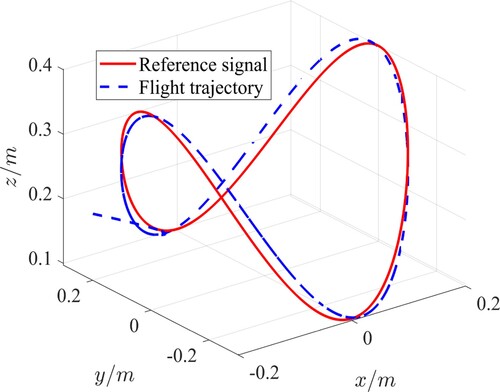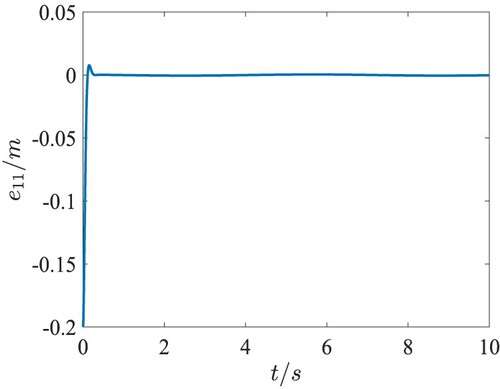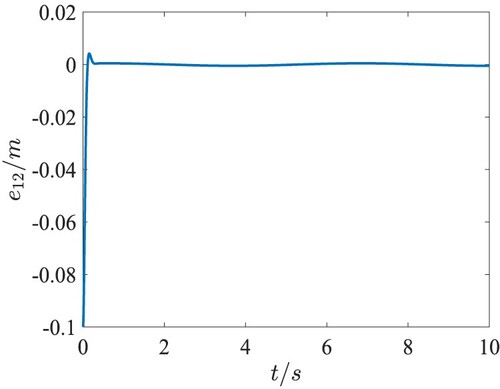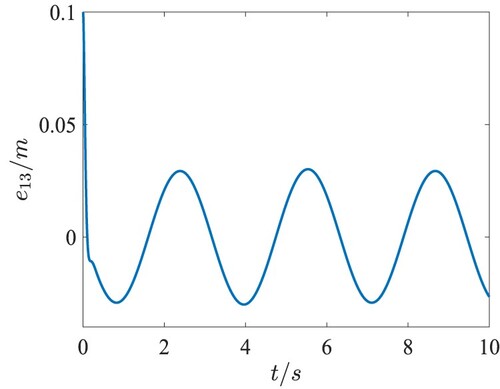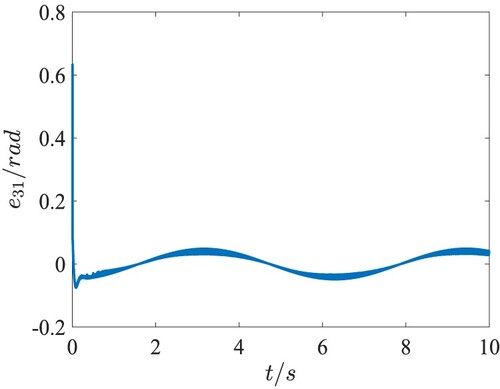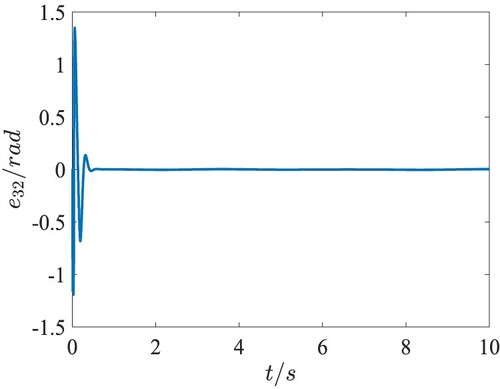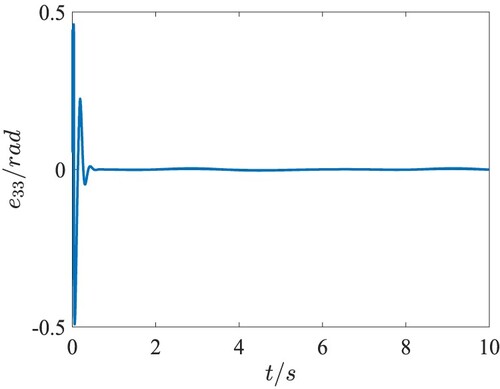The position tracking performance in the 3-D space and the tracking errors in the QUAV position loop are presented in Figures 2–5. Figure 2 shows the fast response and the desired tracking performance in the position subsystem. From Figures 3–5, it can be seen that the tracking errors of X, Y, Z directions are lower than 0.03m after $0.2s$. 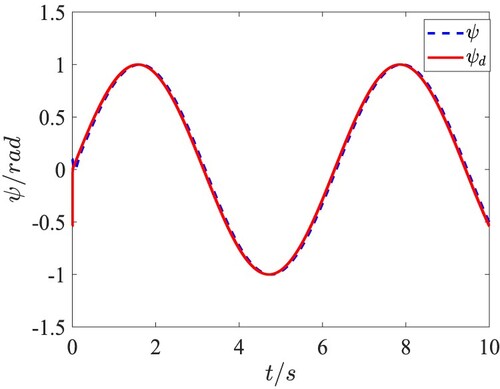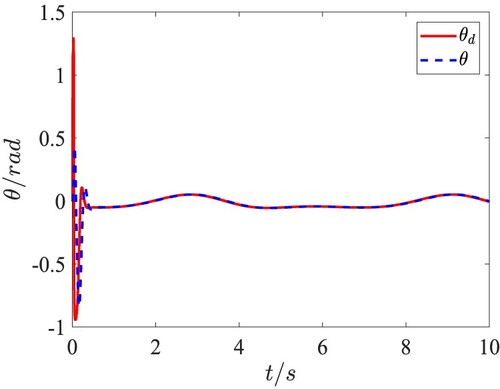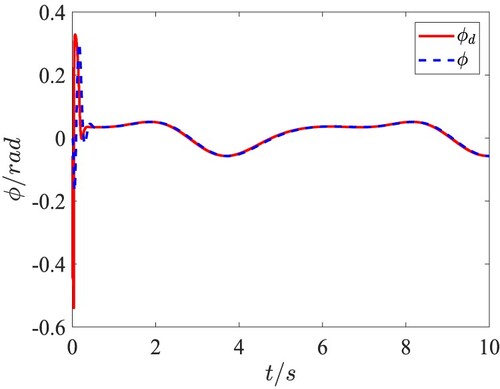The attitude tracking performance and the tracking errors in the QUAV attitude loop are given in Figures 6–11. It is clearly shown that the precise trajectory tracking is achieved with only the fast changes at the moment of taking-off. 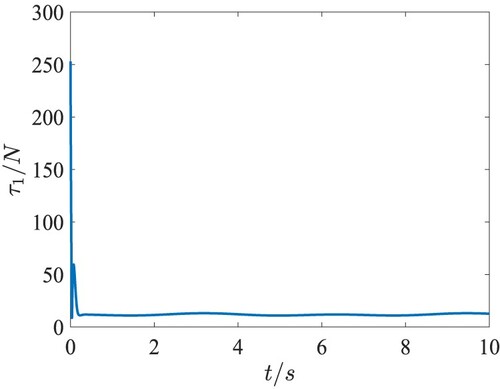Moreover, the tracking error of yaw angle is within $0.05rad$, and the tracking error of roll angle and pitch angle approaches to zero, which meet the actual flight requirements. 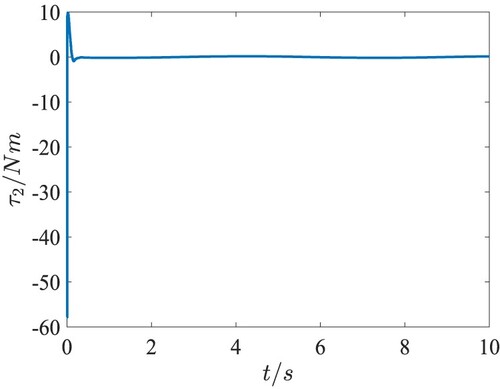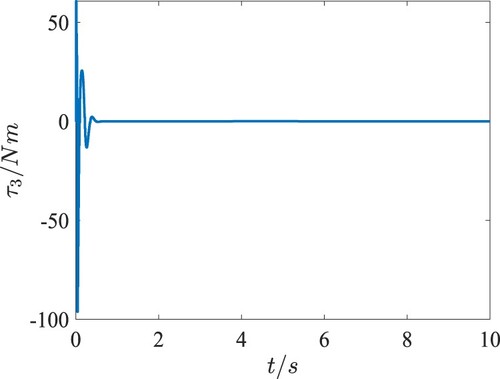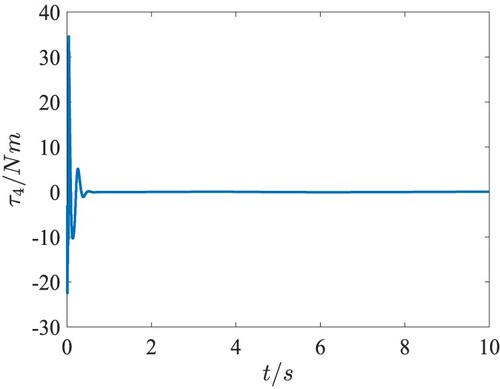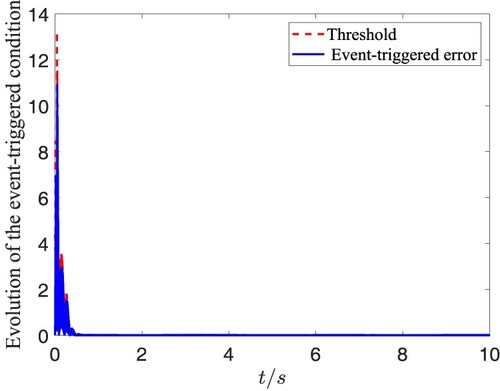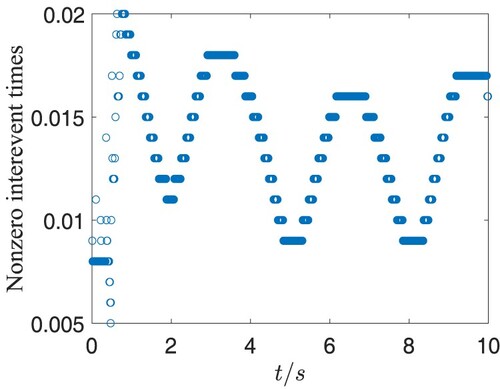The total lift force of the QUAV is depicted in Figure 12, which changes around $12N$ eventually satisfying the practical requirement. The event-triggered torques in the attitude loop are presented in Figures 13–15, and they converge to zero after tracking the desired attitude angles. Figures 16 and 17 provide the interevent time $(t=t_k,k\in Z^{+})$ and the threshold of the event-triggered error, from which we can see Zeno behaviour is excluded in the attitude subsystem under the proposed event-triggered control algorithm. In addition, the event-triggered control algorithm in the attitude loop updated 778 times, while 10,000 times' updating is needed if using the traditional time-triggered control algorithm. Thus, the developed adaptive fuzzy trajectory tracking control not only can guarantee the desired control performance, but also can greatly reduce the number of data transmission by $92.22\mathrm{\%}$.

Figure 2. The position three-dimensional trajectory tracking curve.

Figure 3. The tracking error of the X axis.

Figure 4. The tracking error of the Y axis.

Figure 5. The tracking error of the Z axis.

Figure 6. The tracking curve of the yaw angle ψ.

Figure 7. The tracking curve of the pitch angle θ.

Figure 8. The tracking curve of the roll angle ϕ.

Figure 9. The tracking error of the yaw angle ψ.

Figure 10. The tracking error of the pitch angle θ.

Figure 11. The tracking error of the roll angle ϕ.

Figure 12. The curve of the control input ${\tau }_1$.

Figure 13. The curve of the control input ${\tau }_2$.

Figure 14. The curve of the control input ${\tau }_3$.

Figure 15. The curve of the control input ${\tau }_4$.

Figure 16. The curve of the event-triggered threshold.

Figure 17. The interval of the triggered time.

7. Conclusion

This article studied the trajectory tracking problem for the QUAV system with model nonlinearity and external disturbances. An adaptive fuzzy control algorithm is applied in the position subsystem to provide desired pitch and roll angles for the attitude subsystem. Then, an adaptive fuzzy event-triggered attitude tracking control algorithm is designed, in which the control law and the parameter adaptive law are updated only when the event-triggered error exceeds the given threshold. It is proven that the trajectory tracking of the QUAV is guaranteed under the developed adaptive fuzzy control algorithm. Moreover, the controller updating times and data transmission are greatly reduced, which improves the utilization of the system resources. Future research includes the dynamic ETC based trajectory tracking of the QUAV system or the ETC based cooperative control of multiple QUAV systems.

Disclosure statement

No potential conflict of interest was reported by the authors.

Additional information

Funding

This work is supported by the National Natural Science Foundation [grant number 61603165]; Natural Science Foundation of Science and Technology Department of Liaoning Province [grant number 2019-BS-119].