Breakdown of the superplastic deformation behavior of heterogeneous nanomaterials at small length scales

Abstract

Ultrafine-grained and nanocrystalline materials frequently show an enhanced rate sensitivity of their mechanical behavior, which is generally assumed to be the consequence of interface sliding or thermally activated dislocation processes at the boundaries. Although this has been well documented on many different materials, the underlying mechanisms and their effect on the ductility of the material are still not well understood. Therefore, here, the deformation behavior of the ultrafine-grained, heterogeneous superplastic alloy Zn-22% Al was analyzed by small-scale nanoindentation and micropillar testing. The results show a breakdown of the superplastic deformation behavior in terms of a reduced strain rate sensitivity at small scales, which has not been reported before, although grain boundary sliding is still prevalent at the nanoscale. These results suggest that grain boundary sliding does not necessarily result in a high strain rate sensitivity and high ductility. Instead, a pronounced strain rate dependent flow behavior requires grain boundary sliding to be controlled by dislocation creep.

IMPACT STATEMENT

Superplastic flow is shown to persist down to a small material volume corresponding to a few grains. This has far-reaching consequences for the production of small-scale devices with complex geometries by superplastic forming.

GRAPHICAL ABSTRACT

KEYWORDS:

• Superplasticity
• size effect
• strain rate sensitivity
• nanoindentation
• micropillar

1. Introduction

In recent years, scientific interest in heterogeneous materials as well as ultrafine-grained (ufg) and nanocrystalline (nc) metals and alloys has grown significantly. Both strategies open up novel opportunities for the design of advanced materials with tailored properties. They typically offer higher strength [1–3], hardness [3], toughness [4,5] and ductility [6,7] than both their individual single-phase components and coarse-grained counterparts. In case of heterogeneous systems, these superior properties are the consequence of joining substructures of either different grain sizes [8], crystal structures [9], or atomic compositions [10]. This combination grants the material novel deformation characteristics, triggered by local strain incompatibilities, which result in enhanced properties [11]. In contrast to that, for ufg and nc systems there is a common agreement that the improvements of the mechanical behavior are the consequence of an increased volume fraction of the interfaces [12,13]. However, the involved mechanism and their interaction with internal and external length scales are by far not clear yet. It is relatively well understood that for $d$>1 µm (where $d$ is the mean grain size) plastic flow is governed by dislocations and their piling up at interfaces, whereby for $d$<10 nm grain shearing and grain boundary diffusion are assumed to control plasticity [12,13]. In contrast to this, the transition regime 1 µm>$d$>10 nm appears more complex, since it is dominated by a combination of dislocation driven and interface driven deformation processes, with their respective contribution strongly influenced by changes in grain size.

One example for a class of material that typically fulfills both heterogeneous and ufg conditions are superplastic metallic alloys. Their exceptionally high ductility is usually assumed to arise from a fine grained structure composed of two phases (usually) with distinct crystal structures. Such microstructure is usually produced by an eutectoid phase transformation during an advanced heat treatment of the alloy.

The pronounced ducility directly yields a remarkable forming capacity, resulting in a high relevance of superplastic alloys in various industries. For instance, superplastic sheet forming of metallic alloys plays a significant role in the automotive and aerospace sector, especially where the fabrication of structural components with a complex architecture is required [14–16]. In particular superplastic Al [14,15] as well as Ti-alloys [16,17] have emerged as materials of choice, due to their widespread availability and their exceptional processability. Beside their high ductility and the resulting forming capability, the commercial relevance of superplastic alloys can be attributed to the low residual stresses present after forming.

The remarkable ductility is the consequence of a high strain rate sensitivity $m$ according to (1) $m={\left(\frac{d\left(ln\sigma \right)}{d\left(ln\dot{\epsilon }\right)}\right)}_{T,\epsilon ,Ms}$(1) where $\sigma$ and $\dot{\epsilon }$ represent the flow stress and strain rate in the steady state regime, i.e. at a constant temperature ($T$), strain ($\epsilon$) and microstructure ($Ms$) of the material. The close correlation between a high strain rate sensitivity and a high ductility is well accepted and has been verified on multiple occasions for both superplastic alloys [17] and ufg materials [18]. A true superplastic flow behavior is in general represented by a strain rate sensitivity close to 0.5 resulting in elongations over 400%, due to a retardation of local necking processes [19]. However, this behavior usually only manifests at elevated temperatures ($T>$0.5$T_m$, where $T_m$ is the melting temperature) and low strain rates ($\dot{\epsilon }\ll$0.1 1/s), making it rather irrelevant for industrial applications, due to high tooling costs and a low throughput. In contrast, the use of a preliminary stage of true superplastic flow, which appears at lower temperatures and higher strain rates is of considerably higher economic relevance. Due to a lower strain rate sensitivity, typically close to 0.33, the maximum elongation does not exceed 350% in this regime [19]. Based on the yet remarkably high tensile elongations and therefore exceptional forming capacity, this regime is often designated as the ‘extended ductility’ regime or – albeit sometimes misleadingly – as a superplastic regime in contrast to the true superplastic behavior mentioned above [19].

Similarly to bulk metallic glasses, superplastic materials are interesting candidates for the production of micro and nano devices by microforming processes. However, size effects hinder a simple transfer of know-how across the involved length scales. For instance, from both hardness tests and finite element (FE) calculations on brass, Chen et al. [20] noticed a significant drop of the flow stress when the sample dimension is reduced. Gau et al. [21] drew a similar conclusion from tensile and bending experiments on brass specimens with different dimensions. This decrease of the flow stress is usually attributed to an increase of the ratio between the number of surface and bulk grains, whereby the surface grains are less constrained resulting in a reduced deformation resistance of the whole material.

Possible size effects in terms of the strain rate sensitivity have not been studied in detail so far. Saotome in [22,23] verified the superior formability of a metallic glass above the glass transition temperature in both the micro and nano regimes. This was attributed to the high strain rate sensitivity (close to 1) of the Newtonian viscous flow regime, which is likely to persist at small length scales, due to the highly homogeneous microstructure of the amorphous system. However, due to the typically two-phase ultrafine-grained microstructure, this homogeneity is not necessarily fulfilled for superplastic metallic alloys at length scales of the order of a few mean grain sizes. For this reason, the aim of this work is to analyze the evolution of the strain rate sensitivity of a superplastic metallic alloy from the micro scale towards the nano scale using nanoindentation creep as well as micropillar strain rate jump compression experiments.

2. Materials and methods

All measurements have been performed on the eutectoid alloy Zn-22% Al, containing 78 wt. % Zn and 22 wt. % Al. The as-cast material was subjected to a homogenizing heat treatment at 643 K for 12 h and a subsequent annealing for 20 min at 533 K, followed by quenching in water. This results in a two-phase ultrafine-grained microstructure with a similar grain size for both phases, typically ranging between 200 nm and 1.4 µm. The mean grain size is 640 nm. It is worth mentioning, that this grain size, which is achieved by pure heat treatment, is only slightly larger than as processed by high pressure torsion [24]. Figure 1(a) shows a SEM image of the corresponding microstructure, where the bright and dark phases correspond to a hcp Zn-rich η phase and a fcc Al-rich α phase, respectively. Please note that the dislocation density in the as received material is negligibly small for both phases, as revealed by the STEM image in Figure 1(b). For further microstructural details about this alloy system, the reader is referred to [25].

Figure 1. Microstructure of the investigated alloy Zn-22% Al: (a) SEM image; (b) Bright field STEM image.

For nanoindentation purposes, the material was ground, polished with diamond suspension down to a particle size of 1 µm and finally polished to a mirror like finish using an oxide suspension.

Several micropillars with different diameters $D$ ranging from 1 to 4 µm and a constant aspect ratio of approximately 2.5 were fabricated out of the polished sample using a dual beam focused ion beam workstation (Crossbeam 540, Carl Zeiss Microscopy GmbH). In a first step, a trench with a coarse pillar in the center and an external and inner diameter close to 30 and 7 µm, respectively, was milled using beam currents of 7–15 nA. Afterwards, several polishing steps were performed applying beam currents between 700 and 50 pA, to minimize milling defects and obtain the desired pillar diameter.

Nanoindentation creep as well as micropillar strain rate jump compression experiments were performed to identify the strain rate sensitivity, respectively as a function of the indentation depth and specimen size.

2.1. Nanoindentation creep

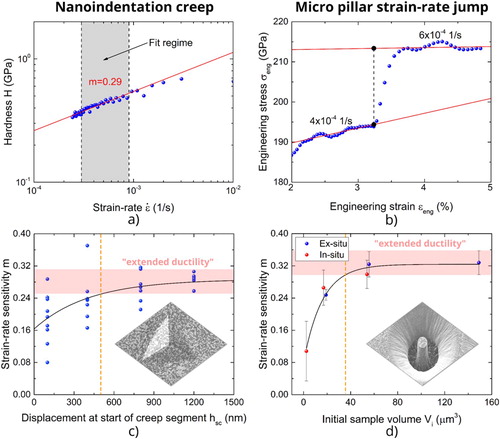
Nanoindentation creep experiments were performed at room temperature with a nanoindenter G200 (KLA-Tencor, CA, USA) by loading the indenter at a constant strain rate [26] up to a specific penetration depth $h_{sc}$ of 100 nm–1200 nm. This initial segment was followed by a creep segment of 10 min, during which the indentation force is maintained at a constant level. The strain rate sensitivity is extracted from the slope of the linear fit of the corresponding plot of the hardness versus strain rate, in a strain rate regime between 3 × 10⁻⁴ /s and 9 × 10⁻⁴ /s (Figure 2(a)). Since the displacement captured by the system might be significantly affected by thermal drift, the hardness as well as the strain rate is determined from a drift corrected penetration depth, derived from the measured contact stiffness and the area function of the Berkovich tip, see [27,28] for more details.

Figure 2. Nanoindentation creep and micropillar strain rate jump tests at room temperatures: (a) Evaluation of the strain rate sensitivity from nanoindentation creep tests ($h_{sc}$=1200 µm); (b) Evaluation of the strain rate sensitivity from micropillar strain rate jump tests ($D$=3 µm); (c) Evolution of the strain rate sensitivity with indentation depth; (d) Strain rate sensitivity as a function of the micropillar volume.

2.2. Micropillar strain rate jump

Micropillar strain rate jump tests were performed ex-situ with the nanoindenter G200 (KLA, CA, USA), as well as in-situ in a scanning electron microscope (SEM, Crossbeam 1540, Zeiss, Germany) utilizing a Picoindenter PI 88 (Bruker Corporation, MA, USA). Due to the high influence of the strain rate on the measured strain rate sensitivity [25], testing strain rates of 2-6 × 10⁻⁴ /s were used, which compare well with the nanoindentation creep experiments. Figure 2(b) shows the corresponding evaluation procedure to determine the strain rate sensitivity from the stress-strain diagram of the micropillars.

3. Results and discussion

3.1. Nanoindentation creep

Figure 2(c) summarizes the measured strain rate sensitivity as a function of the displacement at the start of the creep segment $h_{sc}$. For large indents ($h_{sc}\ge$ 500 nm), $m$ is close to 0.3. This value is in agreement with nanoindentation strain rate jump tests reported in [25], as well as with macroscopic tensile experiments in [29,30], and is assumed to reflect plastic flow governed by a solute drag creep process [19]. As mentioned above, this type of material behavior is typically designated as ‘extended ductility regime’ (ED regime) and corresponds to a superplastic behavior, i.e. a preliminary stage of true superplastic flow, since it is coupled with remarkable tensile elongations exceeding 300% [19]. However, below a critical penetration depth of around 500 nm, the scattering of the measured strain rate sensitivity data increases significantly, while the mean $m$-value substantially decreases. This indicates a change of the rate-controlling process beneath a critical size of the plastic zone and hence the presence of a size effect on the extended ductility regime.

The origin for the pronounced scattering and the lower mean value of the strain rate sensitivity for $h_{sc}$ < 400 nm is not yet totally clear. Part of the scattering is due to the surface roughness of the sample (R_RMS=9 nm) which makes the evaluated contact area and hence nanoindentation hardness data noisier. In addition, it is likely that the scattering of the strain-rate sensitivity data reflects variations of the sampled phases and their respective crystallographic orientation within the plastic zone of the indent. In any case, the likely origin of the overall decrease of the strain rate sensitivity at small indentation depth is the following: while a large variety of different phases, interfaces and grain orientations are contained within the plastic zone of very large indents and trigger superplastic flow, shallow indents rather tend to sample individual phases and grain orientations, which are not able to trigger a superplastic flow behavior on their own, i.e. they rather tend to show convential metallic plasticity, associated with a lower strain-rate sensitivity. However, it is important to note that for all investigated values of $h_{sc}$ the size of the plastic zone by far exceeds the mean grain size and therefore the corresponding $m$-values always represent the contribution of several grains.

Following previous work [25], a FEM calculation of the indentation process was used to estimate the volume of the plastic zone at the critical penetration depth, by applying the commercial simulation package ABAQUS/Standard. A linear elastic, plastic, isotropic material behavior was assumed, with a Younǵs modulus of 85 GPa and a flow behavior taken from a macroscopic tensile experiments. The size of the plastic zone around the indent is hereby determined from a circular fit to the elastic-plastic boundary at an equivalent plastic strain of 0.2%. Based on the mean grain size of 640 nm, the corresponding critical number of grains necessary for the occurrence of superplastic flow is estimated. For this purpose, the superplastic regime was defined as the red-shaded area in Figure 2(c), which corresponds to the macroscopic strain-rate sensitivity of the material (mean value +/- standard deviation), as measured from the deepest indents. After fitting the $m$ versus $h_{sc}$ data with an asymptotic function, a critical penetration depth (dashed orange line in Figure 2(c)) close to 500 nm was determined as the departure from the superplastic regime (defined above). By using this experimentally determined critical penetration depth in conjunction with the corresponding volume of the plastic zone determined by the FE analysis, a cubic volume of 7 grains along the edge length is found to be the lower bound for the occurrence of the extended ductility regime. For further details regarding the FEM simulation and analysis procedure we refer to [25].

3.2. Micropillar strain rate jump

Similar to nanoindentation, the strain rate sensitivity measured by micropillar compression tests exhibits a clear size dependent behavior (Figure 2(d)). Above a critical volume $V_c$ (dashed orange line in Figure 2(d)) of approximately 40 µm³, the specimens behave like macroscopic samples, with $m$ close to 0.3. Beneath this critical size, the strain rate sensitivity steadily decreases, reaching a mean value close to 0.1 for the smallest tested volume of 2.4 µm³. This decrease of $m$ goes along with an increasing scattering in the measurements, as previously observed with nanoindentation creep. This confirms the existence of a size effect on the extended ductility regime. Please note that the force controlled ex-situ experiments using the nanoindenter G200 deliver identical results to the displacement controlled in-situ experiments, at least for volumes larger than 17 µm³. In case of 2.4 µm³ micropillars the required displacement-rates could not be maintained precisely with the G200 system and consequently the strain rate sensitivity is measured in this case solely with the PI 88. The critical pillar volume where the transition from the extended ductility regime to more general plasticity occurs, corresponds to a volume with roughly 6 grains over the edge length, which is nearly identical to the findings from the nanoindentation creep tests. This agreement is remarkable, since the obtained critical volume is the result of two distinct testing methods, creep and strain rate jump testing, in combination with different geometries of the plastic zone, i.e. semi-sphere and rectangular, respectively.

A representative stress-strain diagram as obtained from in-situ experiments on pillars with a volume larger than the critical volume is shown in Figure 3(a). It shows that a change in strain rate is directly associated with a pronounced change of the flow stress level, reflecting the pronounced rate-dependency of the alloy at these length scales. Especially for strains lower than 3%, a significant hardening behavior is evident, most likely due to dislocation hardening coupled with viscous solute drag creep. This flow behavior is reflected by a rather smooth stress-strain curve. However, small stress drops are apparent especially at higher strains, as indicated by the colored arrows. These slight discontinuities are likely coupled with out-of-surface shearing events of individual grains as suggested by the live SEM recordings (Figure 3b, c). As a consequence, the superplastic flow within the extended ductility regime is governed by dislocation creep in combination with grain shearing processes – with the latter one acting at least close to the specimen surface. This high relevance of grain boundary sliding during superplastic flow has been widely confirmed for different materials systems [31–34]. Please note, that the in the superplastic community well-established term ‘grain boundary sliding’, usually also includes the sliding of phase boundaries in case of two-phase superplastic alloys.

Figure 3. Stress-strain behavior and deformed microstructure for exemplary micropillar strain rate jump tests: (a - c) $D$=3 µm ($V>V_c$); (d – f) $D$=1 µm ($V<V_c$).

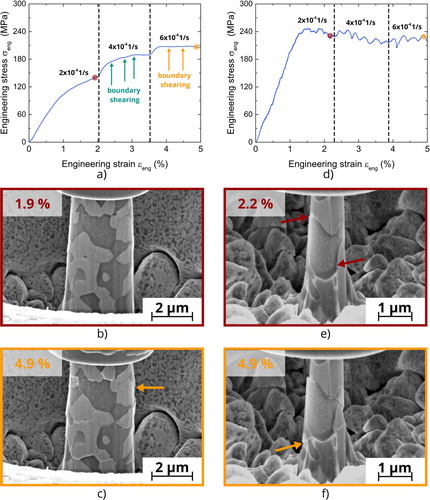
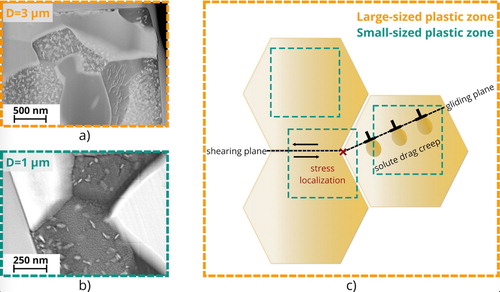
Most of the small micropillars exhibit a serrated flow behavior. Only a few specimens show a smooth stress-strain curve comparable to the behavior observed for the larger pillars, albeit with a slightly reduced rate-dependency. The serrated flow behavior introduces some uncertainty for the determination of the steady state flow stress, which is thought to be one reason for the higher scatter of the $m$-values for small pillar dimensions. A representative serrated stress-strain curve is shown in Figure 3(d). A change of the deformation-rate results in a relatively small change of the flow stress, which is in accordance with the reduced strain rate sensitivity measured at small scale. Nevertheless, the deformed pillars clearly show evidence of interface sliding. This is accompanied with distinct strain-softening. Pronounced stress drops are apparent, which can be correlated with grains shearing relative to each other (Figure 3e,f). The jerky motion is expected to correspond to the repeated obstruction of grain boundary sliding at triple junctions. However, it cannot be excluded that individual pop-in events are the consequence of the temporary activation of single dislocation sources, since not each event could be associated to a sliding interface in the SEM. Nonetheless, the dominant grain boundary sliding processes are assumed to be the origin for the observed strain softening, as also observed by molecular dynamic simulations on nc Ni [35]. Grain boundary sliding events manifest as sudden stress drops, followed by a subsequent loading segment. This suggests a rather discrete nature of sliding events, in contrast to a frictional grain boundary sliding process, as previously shown for nc Al [36]. The dislocation density in both small and large micropillars remains rather low after deformation, see the dark field STEM micrographs shown in Figure 4(a) and (b). In detail, the dislocation density is slightly lower in small specimens. This further highlights the relevance of intercrystalline processes during deformation, including interface sliding and dislocation annihilation.

Figure 4: Deformed microstructure and proposed model for the observed size effect of superplastic flow (for full details the reader is referred to section 3.3): (a) STEM dark field image for a deformed micropillar showing no size effect ($V>V_c$); (b) STEM dark field image for a deformed micropillar exhibiting a size effect ($V<V_c$); (c) Schematics illustrating the origin of the size dependent ductility, as a breakdown of the coupling between boundary sliding and intracrystalline dislocation plasticity for small specimen dimensions.

3.3. Model approach

Figure 4(c) illustrates the proposed model for the observed size effect of the strain rate sensitivity based on the experimental results. Pleaso note that the strain-rate sensitivity solely allows a conclusion in terms of the nature of the rate controlling process and not the phase where deformation occurs. As a consequence, the model is built upon the approximation of a single phase material, which is totally sufficient to explain the origin of the size effect. In case of large specimen volumes, plasticity is governed by interface sliding and intracrystalline dislocation creep. The former process is clearly observed around the edge of the indents and the surface of the deformed pillars. In [37], it was shown that these grain boundary sliding processes are coupled with an increase of the dislocations at the grain boundaries, which was not directly observed here. Therefore, grain boundary sliding needs to be coupled with some dislocation nucleation mechanism, since the initial dislocation density inside the grains is negligibly small. Due to the observed grain shearing processes, stress concentration at triple points between sliding and obstructing grains are likely to be the origin for the nucleation of dislocations inside single grains and the resulting activation of the rate-controlling dislocation drag creep process, resulting in a strain rate sensitivity close to 0.3. The subsequent increase in the dislocation density is directly related to the observed slight strain-hardening at small strains during compression. However, the flow stress saturation at higher strains also suggests an additional dislocation annihilation process during straining. This is consistent with the relatively small dislocation density based on the STEM analysis after testing. The related modifications of the grain morphology open up new possibilities for subsequent boundary sliding processes, and the process starts all over again. However, for specimen volumes smaller than the critical volume, the probability for the occurrence of stress concentrations due to obstructing grains is limited, which is why dislocation nucleation inside the grains is reduced. Therefore, the likelihood for the activation of the intracrystalline dislocation drag mechanism is substantially decreased, resulting in the observed change of the strain rate sensitivity. Hence, it is most important to emphasize that a high occurence of grain boundary sliding does not necessarily yield a high strain rate dependent plastic deformation behavior. In the investigated case of a superplastic alloy, a high strain rate sensitivity is only given when the rate of grain boundary sliding is controlled by dislocation creep, which requires a sufficiently large specimen volume in relation to the grain size. This also emphasizes the importance to distinguish between the dominant deformation mechanism – i.e. the mechanism that contributes most to the overall strain – and the rate controlling deformation process. This is often ignored, e.g. in the field of nanocrystalline plasticity, where the observation of grain boundary sliding is frequently being directly associated with a high strain rate sensitivity.

4. Conclusions

In this work, the size dependent deformation kinetics of the heterogeneous, ultrafine-grained eutectoid alloy Zn-22% Al was characterized using nanoindentation creep as well as micropillar strain rate jump compression testing. The following conclusions are drawn:

• For micro-scale specimen volumes larger than 40 µm³, the investigated alloy exhibits a strain rate sensitivity close to 0.3, consistent with macroscopic data.

• However, for specimen volumes smaller than 40 µm³, a progressive decrease of the strain rate sensitivity is evidenced, which suggests a change of the rate-controlling deformation process and a significant loss of ductility. This is supported by both nanoindentation and micropillar compression experiments. The loss of the strain rate sensitivity happens although strong boundary sliding processes are visible on the surface of the tested volume.

• Hence, the occurence of grain boundary sliding in ultrafine-grained superplastic alloys, and more generally speaking in nanocrystalline materials, should not be arbitrarily associated with the pronounced strain rate dependent deformation behavior generally observed for these materials systems.

Acknowledgements

We acknowledge financial support from Deutsche Forschungsgemeinschaft (DFG) via the research training school GRK1896: ‘In-Situ Microscopy with Electrons, X-rays and Scanning Probes’ and the ‘Center for Nanoanalysis and Electron Microscopy’ (CENEM) at FAU.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

This work was supported by GRK: [Grant Number 1896].