Anharmonic effect on the thermally activated migration of {101̄2} twin interfaces in magnesium

ABSTRACT

Using a recent linear scaling method that fully accounts for anharmonic thermal vibrations, we calculated the activation free energy for $\{10\overline{1}2\}$ twin boundary migration in magnesium up to 450 K, under both resolved shear stresses and non-glide stresses resulting from c-axis tension. Comparing to direct molecular dynamics data, we show that the harmonic transition state theory unexpectedly overestimates the activation entropy above temperatures as low as 100 K, leading to underestimates of the nucleation time by many orders of magnitude. Whilst a specific interface is studied, anharmonic and non-glide effects are expected to be generally significant in thermally activated interface migration.

GRAPHICAL ABSTRACT

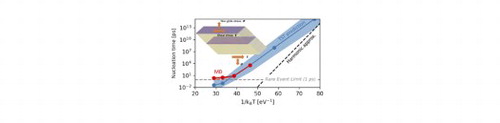
IMPACT STATEMENT

Anharmonic vibrational effects are shown to affect the kinetics of thermally activated processes even at low temperatures, which in the present case leads to an unexpected decrease in the nucleation rate.

Keywords:

• Twinning
• transition state theory
• anharmonicity
• magnesium

1. Introduction

Promoting twinning is one of the main routes to increase the ductility and formability of hexagonal close-packed (HCP) metals and alloys [1–3] and is the subject of intense research [4,5]. Twinning involves the nucleation of a twin embryo, which expands and creates a twin interface. Further growth requires the migration of the twin interface. Surprisingly, although this process is clearly three dimensional (3D), most of the atomic-scale studies of twinning so far have used two-dimensional (2D) configurations, with translational invariance imposed through periodic boundary conditions. Such simplification precludes any quantitative prediction of the interface mobility [6].

Only recently has the 3D structure of the twin embryo been recognized and studied [7,8]. The migration of a twin interface in 3D in an HCP metal has only been studied in two instances [6,9]. In both cases, the $\{10\overline{1}2\}$ twin in magnesium was considered. It was shown by molecular dynamics (MD) simulations that the interface migrates under the action of a resolved shear stress by the thermally activated nucleation and expansion of a disconnection loop on the twin surface. Parameters to describe the twin mobility were extracted from the MD simulations using simplified models, based on the assumption of a square disconnection loop nucleus and a line tension model in Ref. [9] and of a linear stress-enthalpy relation in Ref. [6].

The kinetics of thermally activated processes can be predicted using the transition state theory (TST) [10], often applied in its harmonic approximation (HTST). Anharmonic effects are expected at high temperature, although their magnitude and onset temperature depend on the process at hand. Recently, the projected average force integrator (PAFI) method [11] has been proposed to measure activation free energies accounting for anharmonicity. Moreover, the $O(N)$ scaling of this method allows applications in much larger systems than is typically practical for $O(N^3)$ HTST calculations.

In the present work, we show that the thermally activated mobility of the $\{10\overline{1}2\}$ twin interface can be quantitatively predicted under stress and in 3D using the TST in combination with PAFI calculations of the activation free energy. The calculations are validated on direct MD simulations. We show that anharmonicity plays a crucial role above a temperature which decreases with the applied stress. We consider here the $\{10\overline{1}2\}$ twin interface in magnesium as a case of reference, but the proposed methodology can be used to predict the mobility of other interfaces.

2. Methods

Magnesium was modeled with the modified embedded atom method (MEAM) potential of Wu et al. [12], which has been used extensively to model dislocation cores [13–15], fracture [16] and twinning [6,17].

The simulation cell is shown in Figure 1(a). It is periodic and contains two twinned regions separated by $\{10\overline{1}2\}$ twin boundaries parallel to XY planes. The cell dimensions are $30\times 16\times 15{\mathrm{nm}}^3$ with 320,000 atoms. The $\{10\overline{1}2\}$ twin has a XZ crystallographic shear, $\eta \sim 0.13$ [18]. In order to drive the motion of the twin boundaries, we applied a XZ pure shear stress, τ, by straining the simulation cell. The strain was applied to the initial cell after an initial energy minimization and was held fixed during the simulations.

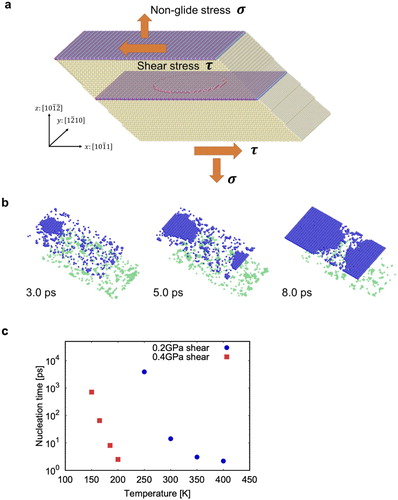
Figure 1. MD simulations: (a) Simulation cell, (b) Example of a migration event observed at $\tau =$ 0.2 GPa and $T=$ 300 K, (c) Average nucleation times at $\tau =$ 0.2 and 0.4 GPa as a function of temperature. The crystallographic basis in (a) refers to the crystal in the lower half of the cell.

We used the LAMMPS package [19] to perform MD simulations at constant temperature and applied strain. We considered two applied stresses, 0.2 and 0.4 GPa and temperatures from 100 to 400 K. The simulations were performed in the NV E ensemble with no thermostat.

In order to predict growth rates, we used the TST. We first identified the minimum energy path associated with an elementary migration event using the nudged elastic band (NEB) method [20]. We constructed initial and final configurations corresponding to the migration of one of the twin boundaries. We then constructed an initial path with composite configurations where atomic positions are taken from the initial configuration except in cylinders of increasing radii where positions are taken from the final configuration. This initial path was first relaxed using the NEB method but showed an abrupt decrease after the saddle point. As a result, the pathway resolution around the saddle point and the accuracy of the activation energy were poor. We therefore extracted the first configuration after the saddle configuration and performed a free-end nudged elastic band (FENEB) calculation [21], with 12 images, a spring constant of 1.0 eV/Å${}^2$ and a force tolerance of ${10}^{-3}$ eV/Å.

The second step was to employ the PAFI method [11,22] to measure the temperature-dependent activation free energy of the process. PAFI calculates the free energy difference $\mathrm{\Delta }\mathcal{F}(r)=\mathcal{F}(r)-\mathcal{F}(0)={\int }_0^r{\mathrm{\partial }}_{r^{\prime }}\mathcal{F}(r^{\prime })\mathrm{d}{r}^{\prime }$ with respect to the NEB coordinate r by performing constrained dynamics on a set of hyperplanes perpendicular to the NEB pathway. By taking the ensemble average of a modified projection of the atomic forces, PAFI is able to reconstruct the free energy gradient, ${\mathrm{\partial }}_r\mathcal{F}(r)$, even when the minimum free energy pathway at finite temperature differs from the NEB pathway.

For the present calculations, we employed 160 CPU cores per worker, with 40 workers per hyperplane, taking averages on 60 hyperplanes for each temperature and applied stress. We note that the high number of hyperplanes could have been reduced by a more judicious choice of the hyperplane positions, with a denser discretization where the force gradient is greater.

3. Results

3.1. MD simulations

Figure 1(b) illustrates a typical MD simulation during which we observed a stress-driven motion of the twin boundaries. The latter involved the nucleation, expansion and coalescence of disconnection loops, as reported previously [6,9]. The disconnections are $b_{2/2}$ disconnections [23] with a height of two $\{10\overline{1}2\}$ interplanar distances, $h\sim 3.86$ Å, and a Burgers vector, $b_{tw}\sim 0.498$ Å [24,25].

The first nucleation event occurs from one to hundreds of picoseconds from the start of the MD simulation. To measure meaningful average nucleation times, we repeated the simulations 20 times for each stress/temperature condition, starting from different random velocities. The result is shown in Figure 1(c). Note that since nucleation is equally likely on both interfaces, nucleation times measured in MD are half those expected for a single interface. The nucleation times reported in Figure 1(c) are thus double those measured in MD.

At high temperatures, the nucleation time is about 1 ps and is comparable with the time required for the system to reach equilibrium from the initial configuration. The shortest nucleation times at high temperature are therefore not controlled by thermal activation, but rather by the equilibration of the system.

3.2. NEB calculations

In order to predict the kinetics of twin migration, we employed the NEB method to compute the twin migration energy under stress. An example of thermally activated path is shown in Figure 2(a). The NEB recovers the formation of an island, which remains fairly circular up to the saddle configuration, in contrast with the square shape assumed in Ref. [9]. Beyond this point, the island starts to feel the underlying crystallography of the $\{10\overline{1}2\}$ plane and the anisotropy of the line tension. The disconnections tend to align along $[10\overline{1}2]$ directions, forming the same edge disconnections as studied in 2D.

Figure 2. FENEB calculations: (a) Example of a minimum energy path computed at $\tau =0.2$ GPa, (b) stress-dependence of the activation energy. The inset in (b) shows the activation surface, computed either from the stress derivative of the activation energy (blue circles) or by counting the number of atoms in the activated island (red circles).

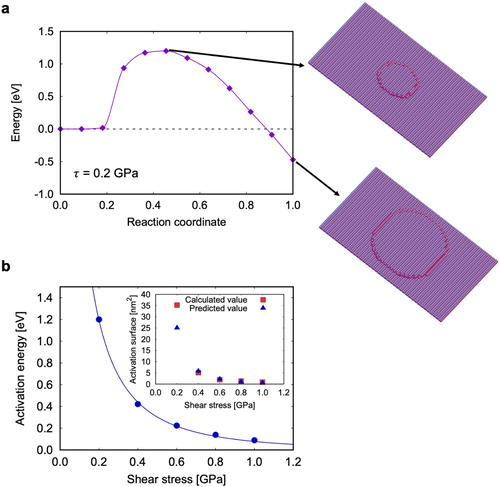
We performed the FENEB calculations for stresses from 0.2 to 1 GPa at intervals of 0.2 GPa. The activation energy decreases rapidly with the applied stress and can be fitted using Kocks law [26]: (1) $\mathrm{\Delta }{E}^{\star }(\tau )=\mathrm{\Delta }{E}_0{(1-{\left(\frac{\tau }{{\tau }_C}\right)}^p)}^q$(1) with $\mathrm{\Delta }{E}_0=146$ eV, ${\tau }_C=82.2$ GPa, p = 0.23, q = 16.9. These parameters are unphysically large, and should only be considered as numerical parameters coming from a phenomenological fit. Note however that the data cannot be accurately fitted by a $1/\tau$ law that would result from a simple line tension model as assumed in Ref. [9].

The activation surface can be computed from the stress dependence of the activation energy: $A^{\star }=-(1/b_{tw}).(d\mathrm{\Delta }{E}^{\star }/d\tau )$. The result is shown in the inset of Figure 2(b), where it is compared with a direct measurement of the island surface in the activated state, obtained by counting the number of atoms in the island, multiplied by the surface per atom. We see that, except at the lowest stress where there may be a finite size effect [9], both measures of the activation surface agree very well.

3.3. Effect of non-glide stresses

A traction or compression along the c axis of an HCP crystal induces on $\{10\overline{1}2\}$ planes, not only a shear stress but also a tensile stress, σ, illustrated in Figure 1. With the notations of Figure 1(a), we have $\tan \alpha =c/\sqrt{3}a\sim 0.94$ and a tensile stress, $\sigma =\tau /\tan \alpha =1.07\tau$. The tensile stress is therefore slightly larger than the shear stress and may affect the migration process in a way analogous to non-glide effects in BCC metals [27–29]. Although non-Schmid effects on twinning have been reported in the literature [30,31], they have not been analyzed at the level of a single twin interface. A detailed analysis is out of the scope of the present work, but in order to estimate potential non-glide effects, we computed NEB paths under combined shear and normal stresses, see Figure 3( b,c). The normal stress has a stronger effect in compression where the activation energy decreases, than in tension, where it increases. Such non-linearity implies a polarization effect [32], probably due to the shuffling component of the twinning process [33,34]. Since $\{10\overline{1}2\}$ twins are seen in tension where the effect of a normal stress remains limited, we will not account for these stresses in the following. We note that $\{10\overline{1}2\}$ twinning-like lattice reorientations have been observed in single-crystal magnesium pillars under c-axis compression [35] and involved the migration of basal/prismatic interfaces, which may be promoted by non-glide stresses.

Figure 3. Non-glide effects: (a) Example of energy path under the combined effect of a 0.4 GPa shear stress and ± 0.2 GPa tensile stresses, (b,c) Tensile stress dependence of the activation energy at (b) 0.2 and (c) 0.4 GPa.

3.4. PAFI calculations

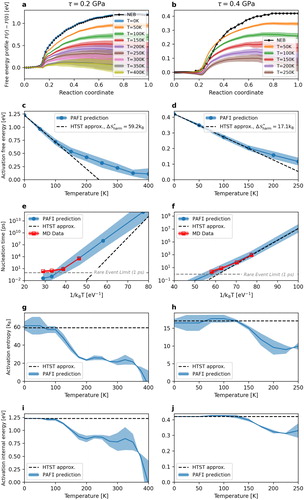
In order to identify anharmonic effects, we employed the PAFI method to measure the temperature-dependent activation free energy of the process. Figure 4( a,b) show the regions of variation of the energy along the finite temperature paths for applied stresses of 0.2 and 0.4 GPa. The average energies are shown as solid lines. We see a gradual decrease in the energy as the temperature increases. The corresponding free energy barriers, $\mathrm{\Delta }{\mathcal{F}}^{\star }$, are shown in Figure 4( c,d). At low temperature, below about 100 K at 0.2 GPa and 150 K at 0.4 GPa, we recover a harmonic regime where the free energy decreases linearly with temperature. At higher temperatures, there are marked anharmonic effects, leading to higher activation free energies compared to the harmonic approximation.

Figure 4. PAFI calculations at $\tau =$ 0.2 and 0.4 GPa: (a,b) Free energy pathways at different temperatures, (c,d) Activation free energy $\mathrm{\Delta }{\mathcal{F}}^{\star }$ as a function of temperature, (e,f) Comparison between predicted and measured nucleation times, (g,h) Activation entropy $\mathrm{\Delta }{S}^{\star }=-d\mathrm{\Delta }{\mathcal{F}}^{\star }/dT$, (i-j)Activation internal energy, $\mathrm{\Delta }{U}^{\star }=\mathrm{\Delta }{\mathcal{F}}^{\star }+T\mathrm{\Delta }{S}^{\star }$.

To predict the nucleation time, we used the expression: (2) $t_{nucl}=t_0\frac{A^{\star }(\tau )}{A}\exp \left(\frac{\mathrm{\Delta }{\mathcal{F}}^{\star }}{k_{B}T}\right).$(2) The term $A/A^{\star }(\tau )$ is a configurational entropy, which estimates the number of independent nucleation sites as the ratio between the area of the interface and that of the activated island. The best fit to the MD data was obtained for $t_0=0.025$ ps. We see in Figure 4( e,f) that the TST expression reproduces accurately the MD data, except, as expected, at high temperatures, where the MD nucleation time saturates at 1 ps and is no longer thermally activated.

4. Discussion

Figure 4(e,f) compares the nucleation times obtained by MD and the PAFI-based TST as well as the extrapolation from the harmonic regime. At 0.2 GPa, all MD data are in the anharmonic regime and the harmonic prediction underestimates the nucleation time by several orders of magnitude. More strikingly, the HTST predicts a vanishing free energy barrier above about 250 K, i.e. spontaneous nucleation, while at this temperature the MD nucleation time is still on the order of several nanoseconds. At 0.4 GPa, the nucleation process is spontaneous at temperatures above 250 K, where the difference between the harmonic and anharmonic predictions is less marked but still on the order of one order of magnitude.

Figure 4(g,h) shows the activation entropy, expressed as $\mathrm{\Delta }{S}^{\star }=-d\mathrm{\Delta }{\mathcal{F}}^{\star }/dT$ and Figure 4(i,j) the internal energy, $\mathrm{\Delta }{U}^{\star }=\mathrm{\Delta }{\mathcal{F}}^{\star }+T\mathrm{\Delta }{S}^{\star }$. The derivatives were computed numerically using finite differences and are somewhat irregular. However, we recover the harmonic regime at low temperature where both $\mathrm{\Delta }{S}^{\star }$ and $\mathrm{\Delta }{U}^{\star }$ are approximately constant, with $(\mathrm{\Delta }{U}_{harm}^{\star },\mathrm{\Delta }{S}_{harm}^{\star })$ equal to $(1.2\mathrm{eV},59.2{\mathrm{k}}_B)$ and $(0.42\mathrm{eV},17.1{\mathrm{k}}_B)$ at 0.2 and 0.4 GPa respectively. We have here approximately a Meyer–Neldel compensation relation [36]: (3) $\mathrm{\Delta }{S}_{harm}^{\star }\simeq \frac{\mathrm{\Delta }{U}_{harm}^{\star }}{T_{MN}}$(3) with a Meyer–Neldel temperature $T_{MN}\sim 275$ K, consistent with the fact that the harmonic free energy barrier, $\mathrm{\Delta }{\mathcal{F}}_{harm}^{\star }=\mathrm{\Delta }{U}_{harm}^{\star }-T\mathrm{\Delta }{S}_{harm}^{\star }=\mathrm{\Delta }{U}_{harm}^{\star }(1-T/T_{MN})$ vanishes at a temperature between 250 and 300 K at both 0.2 and 0.4 GPa (see Figure 4(c,d)). The compensation is probably a consequence of the larger size of the activated island at 0.2 GPa compared to 0.4 GPa, which induces both a larger energy and a stronger perturbation of the vibrational modes of the system.

Interestingly, in the anharmonic regime, $\mathrm{\Delta }{S}^{\star }$ decreases, which is consistent with $\mathrm{\Delta }{\mathcal{F}}^{\star }$ being convex and above its harmonic approximation. This is in contrast with previous calculations on localized defects and dislocations [11], where anharmonicity induced an increase of the activation entropy. An unexpected consequence is that the Meyer–Neldel temperature is here about a third of the melting temperature ($T_m=923$ K), while a usual approximation assumes $T_{NM}=T_m$ [21] and $T_{NM}>T_m$ was found for diffusional processes both in experiments and harmonic calculations [37].

In conclusion, we unveiled strong anharmonic effects in the thermally activated motion of a twin boundary. As the applied stress increases, the harmonic regime is more extended and involves smaller internal energies and vibrational entropies due to the smaller size of the activated island. We expect that this behavior is general and should be true for other stress-driven processes. Finally, how to extrapolate from an isolated twin boundary to situations where multiple twin interfaces migrate simultaneously and interact is a complex issue [38–40], which requires to explore further and formulate the effects of multiple twin boundary migration on the overall strain-rate dependence of twinning. For instance, the effect of the number and size of pre-existing disconnection islands should be investigated.

Acknowledgments

DR thanks Dr. Simon Gelin for insightful discussions on the compensation relation.

Data availability

The data supporting the findings of this work are available from the corresponding author on reasonable request.

Disclosure statement

No potential conflict of interest was reported by the author(s).

Additional information

Funding

YS thanks the support of the JSPS KAKENHI Grant-in-Aid for JSPS Research Fellow [grant number JP19J10309]. SO thanks the support of the JSPS KAKENHI Grant-in-Aid for Scientific Research (A) [grant number JP17H01238] and Grant-in-Aid for Scientific Research on Innovative Areas [grant number JP18H05453]. TDS thanks the Agence Nationale de Recherche for support via the MEMOPAS project ANR-19-CE46-0006-1 and IDRIS for access to HPC resources under allocation A0070910965 attributed by GENCI.