Teacher beliefs about mathematics teaching and learning: Identifying and clarifying three constructs

Abstract

Scholars have long argued that individuals’ beliefs influence their behaviors and the decisions they make throughout their lives. Focusing on beliefs as a cognitive construct, the purpose of this study was to identify several key beliefs about mathematics teaching and learning held by practicing elementary mathematics teachers. An iterative process of literature review, item development and adaptation, expert review of items, and cognitive interviews resulted in 55 items and 5 hypothesized belief constructs. After using the items in a questionnaire completed by more than 200 practicing teachers in two waves of data collection, we modeled the response data using a multiphase process in pursuit of parsimony and a clear factor structure. The resulting 21-item questionnaire provides an alternative measure of Transmissionist beliefs about teaching and a first way to measure two new constructs in teacher beliefs research: Facts First and Fixed Instructional Plan.

Keywords:

• construct validity
• teacher beliefs
• factor analysis
• differential item functioning
• ordinal alpha
• mathematics
• measurement invariance

PUBLIC INTEREST STATEMENT

Many people believe that mathematics teachers must show their students how to solve problems. Others believe that students learn better when they figure out how to solve problems on their own. Some research asserts that students are better at solving real-world problems after they first memorize their arithmetic facts. Other research finds that children learn arithmetic facts with greater understanding when they learn them through solving word problems. Faithful adherence to a fixed curricular plan is highly valued by some educators, while others argue that teachers should continually adjust their scope and sequence of topics—based on their students’ understanding and readiness to learn—to achieve the best learning outcomes. The authors of this article developed a questionnaire to measure elementary mathematics teachers’ beliefs with respect to these seemingly contradictory views. This questionnaire will support efforts to develop a better understanding of how teachers’ beliefs influence teaching and students’ learning.

Scholars have long argued that teachers’ knowledge and beliefs influence their instructional practice (Ball, Thames, & Phelps, 2008; Bandura, 1986; Campbell et al., 2014; Dewey, 1933; Ernest, 1989; Fennema & Franke, 1992; Nisbett & Ross, 1980; Pajares, 1992; Pintrich, 1990; Rokeach, 1968; Shulman, 1986; Wilkins, 2008). In the wake of a shift from the production-function paradigm toward a process-product paradigm, considerable progress has been made over the past 15 years in the development of measures of teachers’ mathematical knowledge for teaching, which is thought to influence instructional practice and student learning (Campbell et al., 2014; Hill, Schilling, & Ball, 2004; Saderholm, Ronau, Brown, & Collins, 2010; Schoen, Bray, Wolfe, Nielsen, & Tazaz, 2017). Most of these assessment tools are designed to measure generalizable facets of mathematical knowledge, but a growing body of research is also beginning to focus on teachers’ real-time, specific knowledge of their individual students’ knowledge and abilities (Gabriele, Joram, & Park, 2016; Hill, Charalambous, & Chin, 2018; Macht, Kaiser, Schmidt, & Möller, 2016; Schoen & Iuhasz-Velez, 2017; SüDkamp, Kaiser, & Möller, 2012). Specific knowledge of individual students is thought to be integral to the process of formative assessment, a process demonstrated to affect student learning significantly (Bennett, 2011; Briggs, Ruiz-Primo, Furtak, & Shepard, 2012; Kingston & Nash, 2011). Some empirical results indicate that teacher knowledge influences instructional practice and student learning, but empirical support for the theorized relation is modest at best (Baumert et al., 2010; Hill, Rowan, & Ball, 2005; Kersting, Givvin, Thompson, Santagata, & Stigler, 2012; Mohr-Schroeder, Ronau, Peters, Lee, & Bush, 2017; Rockoff, Jacob, Kane, & Staiger, 2011; Schoen, Kisa, & Tazaz, 2019).

While much of the focus in published literature on teacher education and professional development in mathematics rests on teachers knowledge of subject matter and how to teach it, many scholars have also acknowledge the importance of teacher beliefs and the relation between knowledge and beliefs (Campbell et al., 2014; Fennema & Franke, 1992; Staub & Stern, 2002; Stipek, Givvin, Salmon, & MacGyvers, 2001). Nespor (1987) posited that beliefs are likely to be far more influential than knowledge in determining how individuals make sense of their world and are likely to be stronger predictors of individuals’ behavior. Pintrich (1990) asserted that both “knowledge and beliefs … influence a wide variety of cognitive processes including memory, comprehension, deduction and induction, problem representation, and problem solution” (p. 836), and he predicted that beliefs would ultimately prove to be the most valuable construct for studying teacher education.

In his review of research on teacher beliefs, Philipp (2007) observed that most of the published studies of teacher beliefs involved qualitative analysis or relatively small samples, and almost all of them involved prospective teachers, not practicing teachers. Although prior work in this area has been invaluable in theory building, the steady work of clarification of teacher belief constructs and development of valid and reliable instruments to measure these constructs efficiently and objectively is needed to allow researchers to test theories about associations between beliefs and behavior (Adler, Ball, Krainer, Lin, & Novatna, 2005; Handal, 2003; Kuntze, 2012; Pajares, 1992; Philipp, 2007).

1.1. Statement of purpose

The dual purposes of the study reported here were to clarify several belief constructs related to mathematics teaching and learning and to create an instrument that can be used efficiently and at a large scale to measure those beliefs in practicing (i.e., in-service) teachers. Because the work was done in the context of an efficacy study of a teacher professional-development program based on Cognitively Guided Instruction (CGI; Carpenter, Fennema, Franke, Levi, & Empson, 1999; Carpenter, Fennema, Peterson, Chiang, & Loef, 1989; Fennema et al., 1996), we aimed to identify beliefs that might be affected by the CGI program or might moderate or mediate the effect of the program on teachers’ instructional practice and, in turn, their students’ learning. In deciding what belief constructs to pursue, we prioritized topics that are relevant to both (a) questions of theoretical interest in scholarly research in mathematics teaching and learning and (b) dilemmas encountered by many or all teachers in the practice of teaching mathematics.

1.2. Defining beliefs

Many scholars have included attitudes, values, dispositions, and other affective constructs in their definitions of beliefs. In attempts to tease these ideas apart, some scholars have offered distinctions among various cognitive or affective components (Goldin, 2002; Jong, Hodges, Royal, & Welder, 2015; McLeod, 1992; Philipp, 2007; Wilkins, 2008). Richardson (1996) defined beliefs as “psychologically held understandings, premises, or propositions about the world that are felt to be true” (p. 103). Other scholars have used phrases such as “belief with certainty” or “justified true belief” in attempts to distinguish knowledge from beliefs (Furinghetti & Pehkonen, 2002; Pajares, 1992; Philipp, 2007; Thompson, 1992). Philipp (2007) provided a useful, albeit general, definition of beliefs when he stated simply that an individual’s belief system provides the framework through which he or she perceives and interprets the world.

Drawing upon the work of Green (1971) and Rokeach (1960, 1968)), Thompson (1992) drew attention to the notion of a belief system as a metaphor for making sense of the complex network of interrelated beliefs that a person may hold. Lewis (1990) argued that knowledge and beliefs are synonymous and that even knowledge derived from the most fundamental perceptual observation is inextricable from evaluative judgment or beliefs.

Bandura (1986) argued that belief constructs and subconstructs are generally too broad and context-free to be useful in research. Pajares (1992) wrote that belief constructs “must be context specific and relevant to the behavior under investigation to be useful to researchers and appropriate for empirical study” (p. 315).

For our immediate purposes, we were particularly interested in identifying beliefs that might influence mathematics teachers’ decision making in the course of their instructional practice. We focused on the cognitive rather than the emotional, affective, or attitudinal facets of beliefs, although we acknowledge the potential importance and influence of emotions, attitudes, and feelings of self-efficacy on instructional practice and student learning (Enochs, Smith, & Huinker, 2000; Ernest, 1989; Ganley, Schoen, LaVenia, & Tazaz, 2019; Hill et al., 2018; Skaalvik & Skaalvik, 2007; Tschannen-Moran & Hoy, 2001). We focused our search for the pedagogical content beliefs that individuals use to create working theories about underlying mechanisms of mathematics teaching and learning that cannot be easily observed or verified. We posit that these beliefs form a default perspective put to use by an individual for the purpose of making decisions when complete information is not (or cannot be) available to the teacher at that time.

1.3. Prior measurement of pedagogical content beliefs in mathematics

Over the past two decades, research involving measurement of teacher beliefs has trended toward specificity with respect to subject matter and context in teaching and learning. In mathematics, several researchers have developed measures of teachers’ pedagogical content beliefs with respect to epistemological beliefs in mathematics, both in general and with respect to specific topics such as algebra or solving word problems (Peterson, Fennema, Carpenter, & Loef, 1989; Nathan, Koedinger, & Tabachneck, 1997). Although most of the extant research focusing on beliefs about mathematics teaching and learning focus on the beliefs held by preservice teachers, some important progress has been made in such investigations focusing on practicing teachers (Campbell et al., 2014; Capraro, 2005; Clark et al., 2014; Collier, 1972; Peterson, Fennema, Carpenter, & Loef, 1989; Philipp et al., 2007; Staub & Stern, 2002; Stipek et al., 2001; Tatto, 2013; Wilkins, 2008; Woolley, Benjamin, & Woolley, 2004).

Many researchers have published questionnaires designed to measure practicing teachers’ beliefs about teaching and learning. Most of the items ask teachers to report on their subject-neutral beliefs about teaching and learning, but some specifically ask teachers about their beliefs about teaching and learning of mathematics or specific topics within mathematics (e.g., Clark et al., 2014; Kuntze, 2012; Nathan et al., 1997; Peterson et al., 1989; Schmidt & Kennedy, 1990; Stipek et al., 2001; Tatto, 2013). We reviewed these questionnaires with the intention of using them, in whole or in part, and found those developed by Peterson et al. to be most closely aligned with our purpose and goals.

Peterson et al. (1989) developed a 48-item questionnaire designed to measure primary-grades teachers’ beliefs related to fundamental components of a program they developed called Cognitively Guided Instruction (CGI). The questionnaire contained four hypothesized constructs. Two of the constructs (Role of the Learner; Role of the Teacher) address general aspects of teaching and learning, and two (Sequencing of Mathematics Instruction; Relationship between Skills, Understanding, and Problem Solving) were specific to the teaching and learning of mathematics. The language in the items on the questionnaire focused specifically on numerical computation and problem solving. Peterson and colleagues administered the questionnaire to 39 first-grade teachers in a midwestern state in the United States in the 1980s, half of whom were participants in the very first group of teachers participating in CGI-based professional development. On the basis of this sample, they reported reliability estimates for of each of the four constructs ranging from .75 to .86 and an overall Cronbach’s α reliability of .93. A modified version of the scale was subsequently developed (Fennema, Carpenter, & Loef, 1990), wherein one of the four subscales was replaced with a set of items developed by Cobb et al. (1991).

The developers of the CGI Beliefs Scale—as the Fennema et al. (1990) survey has come to be known—provided a convincing argument for the interpretation of the resulting scales. They also provided evidence of validity for its intended use in detecting differences among teachers in their sample who had participated in the CGI program (Fennema et al., 1996). They stopped short of conducting a critical investigation of the underlying constructs through factor analysis or other methods.

Several researchers have investigated the factorial validity of the CGI Beliefs Scale. Using a principal-components approach to model data generated from a sample of 123 practicing teachers and 54 prospective teachers in the United States, Capraro (2001, 2005) recommended a more parsimonious set of 18 of the original 48 items. On the basis of findings from her sample, Capraro identified three scales rather than the original four. She identified the items that loaded onto those three scales, but she did not name the factors. On the basis of a sample of German teachers who completed a version of the CGI Beliefs scale translated into German, Staub and Stern (2002) recommended a single underlying factor they called cognitive constructivist—named after the end of the spectrum currently favored by most university-based researchers in mathematics education.

Because the study was conducted within the context of an evaluation of the effect of a CGI-based professional development program on teachers’ beliefs and the role of teacher beliefs as potential mediators of the effect of the CGI program on classroom instruction and student learning, we initially planned to measure teacher beliefs using the CGI Beliefs Scale questionnaire. We thought the primary decision would be whether to use the full set of 48 items or to use the more parsimonious sets of items suggested by Capraro (2005) or by Staub and Stern (2002). We conducted several cognitive interviews with experienced elementary-level teachers in preparation for using the questionnaire and found that the teachers were not interpreting words in the questionnaire in the way in which we thought they were intended by the developers.

1.4. Three emergent constructs: transmissionist, facts first, and fixed instructional plan

We focused our investigation on attempting to identify situations that create dilemmas for teachers as they decide how to teach mathematics in their daily practice. We reviewed items in extant questionnaires designed to measure teacher beliefs in mathematics (Fennema et al., 1990; Philipp et al., 2007; Schmidt & Kennedy, 1990; Stipek et al., 2001; Wilkins, 2008).¹ We selected items, adapted items, and wrote original items. After internal review of the set of new items as well as review by several mathematics teacher-education researchers and elementary teachers, we conducted six cognitive interviews with practicing (i.e., in-service) elementary teachers as they responded to the items in the questionnaire. The cognitive interviews were designed to provide insight into teachers’ interpretation of the items.

One thing we learned from these interviews was the importance of writing the items so that they cause teachers to choose sides. All teachers easily agreed, for example, that students should be allowed to solve mathematics problems in any way that makes sense to them. On the other hand, items written in a way that asked teachers whether they agreed that refraining from showing students how to solve problems is more effective than showing them how resulted in more polarized responses, which yielded considerably more insight into teachers’ beliefs about the topic.

1.4.1. Five initially hypothesized constructs

The item review, item revision, expert review, and interview process yielded a set of 55 items and 5 hypothesized constructs. One set of items was intended to measure a construct related to the relative importance teachers placed on student production of correct answers and on student reasoning processes. The items (and the hypothesized latent construct) for Favoring Correct Answers were dropped from the questionnaire as part of our evaluation and respecification of the measurement model. (See the Results section for further explanation.)

Following the lead of Staub and Stern (2002), we attempted to write items aligned with the Cognitive Constructivist and Direct Transmissionist perspectives as two distinct constructs. These were initially specified to constitute separate (but probably correlated) factors. Subsequent data analyses revealed these factors to be highly, and negatively, correlated. After consideration of model fit and content similarity, we collapsed the items from the two hypothesized constructs into a single factor called Transmissionist. (See the Results section for further explanation.)

We named the other two hypothesized constructs Facts First and Fixed Instructional Plan. These two constructs had empirical support based on participants’ responses to the questionnaire, and they were retained in the final set of items.

At the risk of misrepresenting the chronology of our work, we structure the following sections around the resulting facets of teacher beliefs that we think are measured by the B-MTL questionnaire. After describing those constructs, we will describe the methods of data analysis used to clarify these constructs. Before continuing, we remind the reader of Freudenthal’s famous quote about mathematics. “No mathematical idea has ever been published in the way it was discovered” (Freudenthal, 1983, p. ix). The present article and the findings within it should be interpreted similarly. The sequence of the sections in this article suggests the characterization of these three constructs preceded the field testing of the B-MTL questionnaire, but the actual chronology of the work involved an iterative process.

1.4.2. Transmissionist

One decision teachers must perpetually make is whether—and under what conditions—to tell students how to solve mathematics problems. The mathematics education research literature is replete with examples of researchers imploring teachers to refrain from telling students how to solve mathematics problems, while the mainstream practice of mathematics instruction in the United States involves teachers’ doing just that (Gage, 2009; Stigler & Hiebert, 1999).

Teachers with high levels of Transmissionist beliefs endorse statements consistent with a top-down approach to teaching, whereas those with low levels endorse statements more consistent with a bottom-up approach to teaching and learning (Hiebert & Carpenter, 1992). The top-down approach is the modal form of U.S. mathematics instruction at all levels of formal schooling, and it is generally consistent with what Gage (2009) described as the Conventional-Direct-Recitation (CDR) approach.

Through the work described here, we have come to believe the Transmissionist perspective is the opposite end of the continuum of the scale described by Staub and Stern (2002) as Cognitive Constructivist. Staub and Stern found that students of teachers with a higher self-reported Cognitive Constructivist orientation had higher performance on what they termed structure-oriented tasks. Although they hypothesized that students of teachers with a higher self-reported Transmissionist orientation would perform higher on performance-oriented mathematics tasks, their data failed to confirm that hypothesis. Notably, Peterson et al. (1989) reported similar findings; students of teachers with beliefs that were more aligned the CGI principles had higher scores on a problem-solving test, whereas teachers’ beliefs were not related to students’ abilities to recall number facts. Rather than deferring to the name Cognitive Constructivist, as several scholars before us have done, we name this construct to align with the predominant view of the teachers in our baseline sample.

Teachers with high levels of Transmissionist beliefs endorsed statements that effective teaching involves teachers’ first showing students how to solve problems and students’ then solving problems using the method the teacher presented. Conversely, teachers with low levels of Transmissionist beliefs endorsed statements indicating that effective instruction involves teachers’ encouraging students to solve problems in their own ways and to discuss their solutions with their peers. Teachers with high levels of Transmissionist beliefs agreed that asking students to solve problems in their own way is risky, whereas teachers with low levels agreed with the importance of allowing students to discover how to solve problems in their own, invented ways.

Appendix A displays all the items in this scale that remained after our evaluation of the measurement model and removal of items that did not meet inclusion criteria. The following two items are provided here as examples of items that are consistent with a Transmissionist orientation: “Most students cannot figure out how to solve math problems by themselves and must be explicitly taught,” and “Students should be instructed to solve problems the way the teacher has taught them.”

The sign of the factor loadings reported in Appendix A indicates whether items were positively or negatively associated with the Transmissionist factor. Items in the Transmissionist scale with negative factor loadings were originally written to be aligned positively with the Cognitive Constructivist orientation, which was ultimately combined with the items written for the Transmissionist orientation into a single scale. An example of an item in the Transmissionist scale that was negatively related to the Transmissionist latent trait is “Students can figure out ways to solve many math problems prior to formal instruction.” Agreement with these items with negative factor loadings was associated with low levels of Transmissionist beliefs.

1.4.3. Facts first

Another topic we explored is teachers’ beliefs about the relation and primacy of developing (a) students’ solving word problems and (b) students’ ability to recall number facts and computational procedures. Both of these topics are recurring themes in the items comprising the CGI Beliefs Scale (Fennema et al., 1990) as well as fundamental principles of CGI-based professional development programs (Carpenter et al., 1989; Carpenter & Franke, 2004).

Researchers studying children’s cognition in mathematics have developed two seemingly opposite schools of thought regarding the sequencing of learning of basic facts and solving word problems. One school of thought is based on the assumption that performance in solving of word problems depends upon knowledge of basic facts, where an ability to recall number facts easily is thought to reduce cognitive demand during the solving of word problems (see, e.g., Fuchs et al., 2006). Another school of thought is that students can successfully solve word problems before being able to recall basic facts (Brownell & Chazal, 1935; Carpenter et al., 1999; Kilpatrick, Swafford, & Findell, 2001; Verschaffel & De Corte, 1997). In the latter perspective, children’s understanding of number facts and operations and ability to recall these facts is a consequence of experiences solving word problems rather than a prerequisite.

We provide a simplification of the two assumptions here. The facts-before-word problems approach posits that fact recall provides a basis for solving word problems, because the ability to quickly recall facts reduces the cognitive demand in the complex task of solving word problems. The word-problems-before-facts approach posits that word problems can be successfully solved by students through counting and concrete modeling strategies before they have developed their abilities to recall basic facts, and early experiences solving word problems create opportunities for students to learn about number and operations with a deeper understanding (Hiebert & Carpenter, 1992). Once again, our decision on what to name this construct (i.e., Facts First) was made out of deference to the predominant belief reported by teachers in our sample.

The Facts First scale identifies aspects of teachers’ belief concerning the role of student knowledge of number facts and sequencing topics in instruction for optimal learning. Teachers with high levels of Facts First beliefs endorsed statements indicating that they viewed student knowledge of number facts as fundamentally important. In the Facts First perspective, quick recall of basic number facts is considered a prerequisite to procedural fluency, understanding of the four basic operations, and success in solving of word problems. Teachers who subscribe to the Facts First perspective agree that limited knowledge of basic facts is likely to be the root cause of poor performance in mathematics.

Drawn from the final questionnaire (see Appendix A), the following two items are provided here as examples of statements that are consistent with a Facts First orientation: “Students should master some basic facts before they are expected to solve word problems,” and “Students should master carrying out computational procedures before they are expected to understand why those procedures work.” The original item set included several items designed to be negatively correlated with the latent trait. After eliminating items as part of our evaluation of the measurement model, the only item with a negative factor loading remaining in the Facts First scale is “Even students who have not learned the basic facts can have efficient methods for solving word problems.”

1.4.4. Fixed instructional plan

The third topic we explored and attempted to measure involves an existential problem faced by nearly all mathematics teachers at every level: the omnipresent dilemma about whether to adhere to an externally established scope, sequence, and pacing of the curriculum. Responding to the needs and interests of students is also a fundamental principle in the CGI program, and a strict adherence to an externally imposed, predetermined set of problems and pacing can be antithetical to the formative-assessment practices promoted by the CGI program.

Researchers have found that teachers and instructional leaders view strict adherence to the scope and sequence in the textbook as important features of instruction, particularly in mathematics (Burch & Spillane, 2003; Grossman, P, 1996; Spillane, 2005). After observing both formal and informal conversations among teachers and teacher leaders in both literacy and mathematics, Spillane (2005) reported that conversations about literacy instruction were likely to include detailed discussions of student thinking, flexible use of teaching strategies, and examples of teachers’ gaining substantive knowledge about teaching. In contrast, conversations about teaching mathematics were largely limited to discussions of curricular sequencing and coverage.

These findings suggest that mathematics teachers typically emphasize the sequencing and pacing of topics when they plan for instruction. This point of view has been attributed to beliefs that mathematics must be taught and learned sequentially and in accordance with certain logical assumptions about the hierarchy of topics in mathematics (Thompson, 1992).

Teachers perform their craft as part of a larger social organization, and students take courses that fit into a sequence of mathematics courses. As a result of this system, students are expected to understand a specified set of ideas upon completion of each course. As previous scholars have discussed (e.g., Burch & Spillane, 2003), this expectation is frequently interpreted to mean that teachers must adhere to a fixed, predetermined sequence of topics that does not vary with respect to the individual differences in students’ prior understanding or pace of learning. As a result, teachers must make decisions every day about whether to adhere to a predetermined scope and sequence of topics and activities or to adapt the scope and sequence based upon, for example, students’ understanding and readiness to learn.

The Fixed Instructional Plan beliefs scale represents the extent to which a teacher agrees that teachers should follow the scope and sequence of topics and activities in the mathematics textbook or the school- or district-determined pacing guide. Teachers with high levels of Fixed Instructional Plan beliefs about sequencing topics in instruction agree that students will eventually understand the mathematics if the predetermined, externally imposed scope and sequence in a printed textbook is followed with fidelity. Teachers with low levels of Fixed Instructional Plan beliefs agree that teachers are more effective at helping students to learn when they make adaptations to the prescribed scope and sequence in the textbook or pacing guide based upon their assessment of students’ understanding and instructional needs.

2. Method

2.1. Participants

The analytic sample includes data gathered between summer 2013 and spring 2014 from 207 teacher participants working in 22 schools in two public school districts in Florida. These teachers consented to participate in a cluster-randomized trial of a teacher professional-development program for teachers of primary-grades mathematics students. Eleven of the schools were randomly assigned to the intervention; teacher workshops began in summer 2013. The other 11 schools were assigned to a business-as-usual control condition. The teachers completed our Beliefs about Mathematics Teaching and Learning (B-MTL) questionnaire at the beginning of summer 2013 (Time 1) and at the end of spring 2014 (Time 2). Among the 207 participating teachers, 206 completed the questionnaire at Time 1, 200 completed it at Time 2, and 199 completed it at both times.

Table 1 presents demographic characteristics for the sample at each wave of data collection. Because some analyses were conducted on the control group only, Table 1 provides sample characteristics for the total sample and the control-group subsample. The 207 participants in our study included 95 first-grade teachers, 89 second-grade teachers, and 23 nonclassroom teachers, such as math coaches. All participants were employed in public schools in the state of Florida. The sample mean years of teaching experiences is 11.4 (SD = 8.8), ranging from 0 to 48 years. Each participant held a teaching certificate in either elementary education K–6, primary education PreK–3, special education, or English for speakers of other languages.

Table 1. Sample demographic characteristics at Time 1 and Time 2

	Time 1				Time 2
	Control (n = 105)		Total (N = 206)		Control (n = 105)		Total (N = 200)
	n	%	n	%	n	%	n	%
Gender
Male	0	0.0	3	1.5	0	0.0	3	1.5
Female	105	100.0	203	98.5	105	100.0	197	98.5
Race/Ethnicity^a
Asian	1	1.0	2	1.0	1	1.0	2	1.0
Black	6	5.7	19	9.2	7	6.7	20	10.0
Hispanic	15	14.3	23	11.2	15	14.3	23	11.5
Multiracial	0	0.0	2	1.0	0	0.0	2	1.0
White	82	78.1	159	77.2	81	77.1	152	76.0
Decline to answer	1	1.0	1	0.5	1	1.0	1	0.5
Grade role
1	48	45.7	94	45.6	49	46.7	95	47.5
2	44	41.9	89	43.2	43	41.0	83	41.5
Support	13	12.4	23	11.2	13	12.4	22	11.0
Years of teaching experience
Three or fewer	17	16.2	42	20.4	18	17.1	43	21.5
Four or more	88	83.8	164	79.6	87	82.9	157	78.5
Highest degree earned
Bachelor’s degree	65	61.9	139	67.5	66	62.9	137	68.5
Master’s degree	37	35.2	63	30.6	36	34.3	59	29.5
Professional diploma	2	1.9	3	1.5	2	1.9	3	1.5
Professional degree	1	1.0	1	0.5	1	1.0	1	0.5

Note. Asian = Asian/Pacific Islander, non-Hispanic; Black = Black/African American, non-Hispanic; Hispanic = Hispanic/Latino ethnicity, any racial group; Multiracial = Multiracial or American Indian/Alaskan Native, non-Hispanic; White = White, non-Hispanic; Support = Nonclassroom teachers, such as math coaches.

^aRace and ethnicity are reported here as mutually exclusive categories, consistent with the current reporting methods used in the state of Florida. Teachers self-identified their race and ethnicity.

2.2. Instrumentation

At Time 1, the B-MTL questionnaire was administered in hardcopy by project staff and completed on site by participants in the treatment and control conditions. At Time 2, all participants completed the B-MTL questionnaire through the Qualtrics (2005–2014) on-line survey platform at times and places of their choosing. The form for the questionnaire included 55 items. The sequence of items was determined by random selection, but the sequence was identical for every respondent. The same set of items and same order was used at Time 1 and Time 2. After scale refinement based on analyses of data from both time points, the final questionnaire contained 21 of the original 55 items. The psychometric properties of the final form are presented in the Results section. (See Appendix A for the set of items retained in the respecified questionnaire.)

2.3. Analytic strategy

2.3.1. Overview of phases of data analysis

Analysis of the data from our two field tests of the B-MTL questionnaire consisted of six sequentially linked phases. The analyses involved investigation of evidence of factorial validity, differential item functioning, model parsimony, longitudinal measurement and structural invariance, and scale reliability, providing a comprehensive array of evidence for evaluation of the structural aspects of construct validity (Flake, Pek, & Hehman, 2017). Our aim for Phases 1 through 4 was to identify the best specification for the measurement model and determine whether preliminary validity evidence was present in support of the proposed interpretive argument for the questionnaire. Consistent with the goal of model selection declared by Preacher and Merkle (2012), the purpose of this development stage of investigation was to “find a useful approximating model that (a) fits well, (b) has easily interpretable parameters, (c) approximates reality in as parsimonious a fashion as possible, and (d) can be used as a basis for inference and prediction” (p. 1). Phases 5 and 6 formed an appraisal stage, the aim of which was to assess the psychometric properties of the respecified questionnaire.

In the first phase of analysis, we fit the data to our a priori five-factor model using item factor analysis (IFA; confirmatory factor analysis with ordered-categorical indicators). The aim of Phase 1 was to identify a measurement model that met conventional criteria for factorial validity. In the second phase, we inspected for item bias attributable to treatment condition. In the third, we fit the respecified model to an IFA at two time points to inspect items for longitudinal factor-loading noninvariance. In the fourth, we inspected the structure of the model to ensure that it was as parsimonious as possible without significant reduction in model fit. We followed an iterative approach to model respecification throughout Phases 1 through 4, applying respecifications suggested by one phase before going on to the next. In each phase, both empirical findings and item content were taken under consideration before the model was respecified.

In the fifth phase, we assessed reliability of the respecified scales by calculating conventional and ordinal forms of Cronbach’s α, Revelle’s β, and McDonald’s ω_h (omega hierarchical; Gadermann, Guhn, & Zumbo, 2012; Zinbarg, Revelle, Yovel, & Li, 2005). In the sixth, we fit the measurement model to an IFA at two time points. The Phase 6 modeling technique was the same as that employed in Phase 3, except that in Phase 6 we inspected for all aspects of longitudinal measurement and structural invariance. All analyses were performed with Mplus Version 7.11 (L. K. Muthén & Muthén, 1998–2012), with the exception of the calculation of the reliability coefficients, which were performed in R 3.1.2 (R Development Core Team, 2014) with the psych package (Revelle, 2016) alpha, splithalf, omega, and polychoric functions. Unless stated otherwise, models fit in Mplus used the WLSMV robust weighted least squares estimator.

2.3.2. Criteria used in determining the best specification for the measurement model

Following guidelines outlined by Brown (2015), we evaluated model fit on the basis of overall goodness of fit; presence of localized areas of strain in the solution; and interpretability, size, and statistical significance of the parameter estimates.

2.3.3. Overall goodness of fit

We used the model chi-square (χ²), root mean square error of approximation (RMSEA), comparative fit index (CFI), and Tucker-Lewis index (TLI) to evaluate overall goodness of fit. The χ² statistic is an absolute measure of fit that provides a test of exact fit: a hypothesis test that was argued by Hu and Bentler (1998) to be “too strong to be realistic” (p. 425). A χ² p value < .05 confers an assumption that the model covariance matrix does not match the data perfectly. In keeping with convention, we report the χ² index but devote most of our interest to the other, more practical, indices—which indicate whether the model provides not an exact but a reasonable fit to the data. Although also an absolute measure of fit, the RMSEA differs from the χ² in that the RMSEA is a parsimony-adjusted index and the statistical test is against a hypothesis not of exact fit (i.e., RMSEA = 0) but of close fit. Following guidelines in the structural equation modeling literature (Browne & Cudeck, 1992; MacCallum, Browne, & Sugawara, 1996), we interpreted RMSEA values of .05, .08, and .10 as thresholds of close, reasonable, and mediocre model fit, respectively, and interpreted values > .10 to indicate poor model fit. The CFI and TLI are incremental measures of fit that compare against a baseline, more parsimonious model. Drawing from findings and observations noted in the literature (Bentler & Bonett, 1980; Hu & Bentler, 1999), we interpreted CFI and TLI values of .95 and .90 as thresholds of close and reasonable fit, respectively, and interpreted values < .90 to indicate poor model fit. Although we recognize cautions associated with universal cutoff values to determine model adequacy (from, e.g., Chen, Curran, Bollen, Kirby, & Paxton, 2008; Marsh, Hau, & Wen, 2004), the need for decision rules compelled us to follow conventions of practice and the guidance available in related literature (Lance, Butts, & Michels, 2006). We note findings from simulation studies (Chen et al., 2008; Hu & Bentler, 1999) that tests of RMSEA > .05 and TLI < .95 tended to overreject with small sample sizes (N < 250). Given the size of our sample, therefore, we remain cognizant that the RMSEA and TLI indices may be conservative indicators of model fit and therefore regard the CFI index as perhaps the most trustworthy measure of model adequacy for our sample.

2.3.4. Presence of localized areas of strain in the solution

We inspected for model misspecification by using the combination of modification indices (MI) and expected parameter change (EPC) associated with freeing cross-loadings or error covariance. We constructed 95% confidence for the EPCs using the formula provided by Saris, Satorra, and van der Veld (2009) and applied their suggested factor loading and error covariance critical cutoff values of .4 and .1, respectively, as substantively important deviations indicating model misspecification.

2.3.5. Interpretability, size, and statistical significance of the parameter estimates

Factor analysis models with standardized factor loadings >.7 in absolute value are optimal, as they ensure that at least 50% of the variance in responses is explained by the specified latent trait. In practice, however, this criterion can be too stringent to allow the content representativeness intended for many scales. Researchers working with applied measurement (e.g., Reise, Horan, & Blanchard, 2011) have used standardized factor loadings as low as .5 in absolute value as a threshold for item salience. In accordance with this practice, with scaling set by fixing the variance for each factor to 1, we only retained items that had standardized factor loading estimates ≥ .5 in absolute value with unstandardized factor loading p values < .05.

2.3.6. Item bias

Given our immediate objective of developing a measure to be used in the evaluation of a particular professional-development program, we wanted to identify and remove any item with bias associated with treatment condition. We employed Wang and Shih (2010) pure anchor multiple indicators–multiple causes (MIMIC) method for assessing uniform differential item functioning (DIF) in polytomous items. This process involved a first step of identifying a pure anchor of DIF-free items and a second step of evaluating the nonanchor items for DIF, termed the DIF-free-then-DIF strategy. The first step involved fitting a single-level factor model for as many items as were specified in the model, each model differing from the others in which items were specified as DIF-free. Controlling for the effect of the latent trait, the direct effect of treatment on each item indicated the magnitude and direction of DIF; the absolute value of the direct effect is termed the DIF index. Referencing the mean of each item’s DIF index from across all runs, we identified the item within each scale with the lowest mean DIF to serve as the pure anchor. In the second step, therefore, a subset of items served as the pure anchor: one item from each scale. In the second step, where nonanchor items were evaluated for DIF, the model was specified as a two-level doubly-latent model (Marsh et al., 2009), with random thresholds and slopes that varied across schools and the mean for each within-level slope held equal to the corresponding between-level slope. We used the Educational Testing Service DIF classification (Zwick, 2012) to identify items with moderate to large DIF (i.e., p < .05, odds ratio < 0.528 or > 1.893). Items identified as having moderate to large DIF were removed from the model.

Because the sample size was small relative to the number of parameters to estimate, we used a Bayesian estimator for all DIF analyses. All models were specified with noninformative priors and zero cross-loadings. Model convergence was determined on the basis of satisfaction of the Gelman-Rubin potential scale reduction (PSR) < 1.05 criterion and failure to be rejected in the Kolmogorov-Smirnov distribution test (Kaplan & Depaoli, 2012; L. K. Muthén & Muthén, 1998–2012). Because we were investigating the potential bias introduced by participating in the intervention, DIF analyses were conducted only with data from Time 2 and included data from the project treatment and control group.

2.3.7. Model parsimony

After evaluating the measurement specifications of the model, we evaluated the model’s structural specification. With the objective of specifying a model that was no more complex than empirically and theoretically justified, we inspected the latent variable intercorrelations for indication of collinearity. We fit an alternate specification of the model that combined plausibly collinear factors and used the Bayesian information criterion (BIC; Schwarz, 1978) approximation of the Bayes factor to assess the strength of evidence in favor of the more parsimonious model. Using the formulation specified by Masyn (2013), we calculated the Bayes factor (BF) as

(1) $B{F_{H0,H1}}_{\hspace{0.17em}}=exp\left[SI{C}_{H0}-SI{C}_{H1}\right],$(1)

where SIC is the Schwarz information criterion, given by

(2) $SI{C}_{\hspace{0.17em}}=-0.5BI{C}_{.}$(2)

To interpret the strength of evidence, we applied Jeffrey’s scale of evidence (Wasserman, 2000), which denotes BF_H0,H1 < 1/10, 1/10 < BF_H0,H1 < 1/3, and 1/3 < BF_H0,H1 < 1 as strong, moderate, and weak evidence, respectively, in favor of the H1 less constrained model and 1 < BF_H0,H1 < 3, 3 < BF_H0,H1 < 10, and BF_H0,H1 > 10 as weak, moderate, and strong evidence, respectively, in favor of the H0 more parsimonious model. Models were fit by means of the Mplus MLR maximum likelihood with robust standard errors estimator. Model parsimony was assessed on the basis of data from the treatment and control groups combined, generating factor correlation estimates for Time 1 and Time 2.

2.3.8. Criteria used for evaluating the psychometric properties of the questionnaire

2.3.8.1. Scale reliability

Caution against the routine use of Cronbach’s α over other reliability coefficients has been the subject of much discussion in recent literature (e.g., Sijtsma, 2009). Zumbo, Gadermann, and Zeisser (2007) demonstrated that Cronbach’s α can be downwardly biased when applied to ordinal data, because of its use of a Pearson correlation matrix and corresponding assumption of continuity. Zumbo et al. found ordinal coefficients (hereafter, nonlinear coefficients), calculated with the use of polychoric correlation matrices, to be suitable alternatives to the conventional Cronbach’s α (i.e., linear α) when researchers are working with Likert-type data. Also inherent to Cronbach’s α is the assumption of essential tau equivalence. Zinbarg et al. (2005) demonstrated that comparisons among coefficients α, β, and ω_h can be used to reveal scale properties, such as unidimensionality and equality of factor loadings, that remain unreported when researchers calculate only the α reliability.

Cronbach’s α is mathematically equivalent to the mean of all possible split half reliabilities and conveys how strongly a measure will be correlated with another measure comprising items sampled from the same domain. Revelle’s β is the lowest split half reliability and conveys a measure’s homogeneity. Only when essential Tau equivalence is achieved (i.e., unidimensionality and equality of factor loadings) will α equal β; otherwise, α will always be greater than β, the magnitude of the discrepancy indicating the extent of factor-loading heterogeneity. Variability in factor loadings can be attributable to microstructures in the data, what Revelle (1979) termed lumpiness. McDonald’s ω_h models lumpiness in the data through a bifactor structure and indicates (a) the extent to which all the indicators forming the scale measure a latent variable in common and (b) the extent to which the proportion of variance in the scale scores accounted for by the latent variable is common to all the indicators (Zinbarg, Yovel, Revelle, & McDonald, 2006). The relation between α and ω_h is more dynamic than that between α and β, as α can be greater than, equal to, or less than ω_h, as a result of the particular combination of scale dimensionality and factor-loading variability. We investigated these scale properties by examining the relation among coefficients α, β, and ω_h through the four-type heuristic proposed by Zinbarg et al. (2005). To evaluate reliability coefficients, we apply the conventional values of .7 and .8 as the minimum and target thresholds for scale reliability, respectively (Nunnally & Bernstein, 1994; Streiner, 2003). Reliability was assessed on the basis of data from the project treatment and control groups combined, generating estimates for Time 1 and Time 2. For the reliability analyses, we rekeyed items so that all items were going in the same conceptual direction, and thus all items were positively correlated with the latent trait.

2.3.8.2. Longitudinal measurement and structural invariance

For all tests of longitudinal invariance (performed during Phases 3 and 6 of the investigation), we fit an IFA at two time points with correlated residuals for the same indicators across time. For Phase 3, the test was of invariance of factor loadings only. For Phase 6, the test was of factor loadings, item thresholds, residual variances, factor variances, factor covariances, and factor means. We used a bottom-up (or forward) approach, which starts with noninvariance and compares with models with invariance constraints imposed. Accordingly, a statistically significant test statistic indicates the given constraint resulted in a significantly worse fitting model. Where full invariance was not established, partial invariance was investigated. Our testing procedure followed guidelines suggested by Millsap and colleagues (Millsap, 2011; Millsap & Yun-Tein, 2004; Yoon & Millsap, 2007) and Mplus syntax developed by Lesa Hoffman (http://www.lesahoffman.com/).

Appendix B delineates the model specification for each step in our invariance testing procedure. All invariance models were fit by means of the Mplus WLSMV estimator. In addition to referencing the Mplus DIFFTEST option for model comparison, we applied Chen’s (2007) ΔRMSEA and ΔCFI cutoffs of ≥ .010 and ≤—.005, respectively, for indicating noninvariance of loadings, intercepts (here, thresholds), and residual variance. Longitudinal measurement and structural invariance was assessed on the basis of data from the project control group only; data from Time 1 and Time 2 were modeled jointly.

3. Results

3.1. Phase 1: factorial validity

3.1.1. Evaluation of the a priori measurement model

Model fit statistics for the a priori model were mixed; the RMSEA indicated reasonable fit, but the CFI and TLI indicated poor fit. Time 1 (N = 206) fit statistics for the a priori model were χ²(1420) = 2178.580, p < .001; RMSEA = .051, 90% CI [.047, .055], CFI = .878; and TLI = .873. At Time 2 (N = 200), they were χ²(1420) = 2775.122, p < .001; RMSEA = .069, 90% CI [.065, .073]; CFI = .899; and TLI = .895. Roughly half of the items had low standardized factor loadings (<.5 in absolute value), so half of the items were not salient to the constructs being modeled.

3.1.2. Model fit after phase 1 respecification

Following the criteria to remove items with standardized factor loadings <.5 in absolute value or unstandardized factor loading p values ≥.05 at either Time 1 or Time 2 resulted in dropping 27 of the original 55 items. Dropped items included all 9 items from the proposed Favoring Correct Answers scale, 6 of the 11 from the Cognitive Constructivist scale, 4 of the 14 from the Direct Transmissionist scale, 4 of the 11 from the Facts First scale, and 4 of the 10 from the Fixed Instructional Plan scale. The respecified four-factor model was fit to each wave of data. Time 1 fit statistics after the Phase 1 respecification were χ²(344) = 637.340, p < .001; RMSEA = .064; 90% CI [.057, .072]; CFI = .938; and TLI = .932. Time 2 fit statistics for the respecified model were χ²(344) = 798.088, p < .001; RMSEA = .081; 90% CI [.074, .089]; CFI = .947; and TLI = .942. Model fit statistics after Phase 1 respecification indicated a reasonable fit to the data, providing sufficient evidence of factorial validity to proceed with subsequent phases of investigation.

3.2. Phase 2: differential item functioning

Using the 28-item four-factor model respecified in Phase 1, we investigated the data for item bias. Applying the Wang and Shih (2010) DIF-free-then-DIF strategy, we identified four items with moderate to large DIF: two from the Direct Transmissionist scale and two from the Facts First scale. The two Transmissionist DIF items were both biased toward the control group (OR = .43, p = .016, and OR = 0.40, p = .023, respectively), indicating that odds of endorsing these statements were higher for the control group than for the treatment group, when their level of Transmissionist belief was controlled for. Stated differently, a control group participant had higher odds of endorsing these statements than a treatment group participant of the same Transmissionist beliefs. The two Facts First DIF items were both biased toward the Treatment group (OR = 1.91, p = .032, and OR = 2.53, p = .045, respectively), indicating that odds of endorsing these statements were higher for the treatment group than for the control group, controlling for their level of Facts First belief. The four DIF items were subsequently removed from their respective scales. For all models at Step 1 and Step 2 of the DIF-free-then-DIF procedure, model convergence was achieved, indicated by satisfaction of the PSR < 1.05 criterion and failure to reject the equality of posterior distributions in the Markov chain Monte Carlo (MCMC) chains by the Kolmogorov-Smirnov distribution test. Models were specified with two MCMC chains and a maximum of 200,000 iterations.

3.3. Phase 3: longitudinal metric invariance

Using the 24-item four-factor model respecified in Phase 2, we then investigated the data for longitudinal noninvariance of factor loadings. We identified three items to be metrically noninvariant across time. After conducting nested model comparisons, we found a significant decrease in model fit when all factor loadings were constrained to be equal across time: DIFFTEST (20) = 44.57, p = .002. We successively freed the equality constraint for three items with modification indices that suggested areas of localized strain in the model. DIFFTEST results for each successively freed equality constraint were as follows: 34.82 (19), p = .015; 29.12 (18), p = .047; and 22.63 (17), p = .162. The three metrically noninvariant items (one item from each of the Cognitive Constructivist, Direct Transmissionist, and Fixed Instructional Plan scales) were subsequently removed from the model.

3.4. Phase 4: model parsimony

Using the 21-item, four-factor model respecified in Phase 3, we inspected the structure of the model to ensure that it was as parsimonious as possible without significant reduction in model fit. Table 2 shows factor correlations at Time 1 and Time 2. Although all factors had moderate to high correlations, the factors for Cognitive Constructivist and Direct Transmissionist were notably high, albeit negatively related: Time 1 r = –.89, 95% CI [–.82, –.97]; Time 2 r = –.94, 95% CI [–.89, –1.00]. From inspection of the item content for the remaining items for these scales, we concluded it plausible that the respecified Cognitive Constructivist and Direct Transmissionist scales represented opposing sides of a single construct. Accordingly, we fit separate models, comparing three- and four-factor models at both time points, to determine which provided the best relative fit to the data—collapsing the Cognitive Constructivist and Direct Transmissionist scales or modeling them as separate but correlated factors. High correlations were also observed between the Facts First factor and the Cognitive Constructivist and Direct Transmissionist factors, but we determined the item content for the Facts First scale to be distinct and refrained from model comparisons on collapsing Facts First into one or both of these scales.

Table 2. Beliefs about Mathematics Teaching and Learning Questionnaire Factor Correlations at Times 1 and 2

	Cognitive constructivist		Direct transmissionist		Facts first
	r	95% CI	r	95% CI	r	95% CI
Time 1 (n = 206)
Cognitive constructivist	—	—
Direct transmissionist	–.89	[–.82–.97]	—	—
Facts first	–.63	[–.48–.78]	.82	[.71, .94]	—	—
Fixed instructional plan	–.47	[–.31,–63]	.60	[.46, .75]	.56	[.40, .73]
Time 2 (n = 200)
Cognitive constructivist	—	—
Direct transmissionist	–.94	[–.89,—1.00]	—	—
Facts first	–.88	[–.81,–.95]	.87	[.81, .93]	—	—
Fixed instructional plan	–.57	[–.43–.71]	.69	[.58, .81]	.59	[.45, .73]

Note. Confidence interval lower and upper bounds are ordered by absolute value.

Fitting the data to the H0 more parsimonious three-factor model and the H1 less constrained four-factor model produced fit estimates of BIC_H0 = 8491.17 and BIC_H1 = 8483.97 for data at Time 1 and BIC_H0 = 7733.08 and BIC_H1 = 7736.44 for data at Time 2. The approximate Bayes factor was BF = 0.03 at Time 1, providing strong evidence in favor of the four-factor model, and BF = 5.38 at Time 2, providing moderate evidence in favor of the three-factor model. Although the strength of evidence at Time 1 in favor of the four-factor model is compelling, given (a) our preference for parsimony where justified, (b) a moderate strength of evidence at Time 2 in favor of the more parsimonious three-factor model, (c) the correlation between the factors of concern approximating or exceeding an absolute value of .9 at both time points, and (d) similarity of item content across the respective factors, we adopted the more parsimonious three-factor specification to constitute the final configuration for the B-MTL measurement model.

3.5. Model evaluation of the final configuration

Our inspection of overall goodness of fit, localized areas of strain, and interpretability of parameter estimates found evidence of factorial validity for the final model configuration. The Time 1 RMSEA and TLI indicated reasonable fit and the CFI indicated close fit: χ²(186) = 347.157, p < .001; RMSEA = .065; 90% CI [.054, .075]; CFI = .954; and TLI = .948. The Time 2 RMSEA indicated mediocre fit and the CFI and TLI indicated reasonable fit: χ²(186) = 515.796, p < .001; RMSEA = .094; 90% CI [.085, .104]; CFI = .948; and TLI = .941. Placing greater weight on the CFI index (given research findings of bias with the RMSEA and TLI for sample sizes < 250) suggested an overall reasonable fit to the data. We note that, with the inclusion of school fixed effects controlling for school mean differences in the latent traits, all fit indices at both time points indicated close fit to the data, including failure to reject the χ² test.²

Our inspection for localized areas of strain for the final configuration found no cross-loadings or error covariances that were present at both Time 1 and Time 2. Specifically, using a critical-deviation value of .4 for factor loadings and 95% CIs for the EPCs, no cross-loadings were suggested at Time 1 and only one cross-loading was suggested at Time 2. The same procedure for error covariances, except with a critical deviation value of .1, suggested nine error covariances for Time 1 and 11 error covariances for Time 2. No same-pairing of items was suggested for both time points. With the absence of any indication of systematic misspecification across time and an interest in avoiding overfitting of the model, we refrained from specifying any of the suggested time-specific cross-loadings or error covariances.

Our inspection of the size and statistical significance of the parameter estimates for the final configuration found all items at both time points to have unstandardized factor loading with p-values < .001. Standardized loadings for the Transmissionist factor ranged from .60 to .88 in absolute value (M|λ| = .69, SD = .09) at Time 1 and from .61 to .83 in absolute value (M|λ| = .73, SD = .06) at Time 2. Standardized loadings for the Facts First factor ranged from .53 to .67 in absolute value (M|λ| = .60, SD = .06) at Time 1 and from .68 to .82 in absolute value (M|λ| = .75, SD = .06) at Time 2. Standardized loadings for the Fixed Instructional Plan factor ranged from .65 to .77 (M|λ| = .72, SD = .06) at Time 1 and from .56 to .84 (M|λ| = .70, SD = .10) at Time 2. Appendix A displays all of the items retained in the final model and the respective standardized factor loadings at each time point. The factor correlations ranged from .59 to .78 at Time 1 and from .62 to .91 at Time 2. At both time points, the lowest correlation was between the Facts First and Fixed Instructional Plan factors and the highest correlation was between the Facts First and Transmissionist factors.

3.6. Phase 5: scale reliability

Using the 21-item three-factor model respecified in Phase 4, constituting the final configuration, we assessed scale reliability by calculating linear and nonlinear forms of Cronbach’s α, Revelle’s β, and McDonald’s ω_h. Table 3 displays the reliability coefficients for each scale at Time 1 and Time 2. Consistent with findings by Zumbo et al. (2007), the nonlinear α coefficients, which are calculated by means of a polychoric correlation matrix, produced larger estimates than those of the conventional Cronbach’s α (i.e., linear α). Nevertheless, the disparity between the linear and nonlinear αs was not large (range .01 to .04), suggesting that the data produced by the five-category Likert response scale did not differ drastically from what would have been produced by an interval response scale. The nonlinear α coefficients were generally in the acceptable range; estimates were as follows: Transmissionist (Time 1 α = .88; Time 2 α = .92), Facts First (Time 1 α = .68; Time 2 α = .83), and Fixed Instructional Plan (Time 1 α = .79; Time 2 α = .80). For only one scale and at one time point (Facts First at Time 1) did the estimated nonlinear α not exceed the conventional minimum threshold of .7.

Table 3. Comparison of reliability coefficients for each scale at Times 1 and 2

Coefficient	Time 1 (N = 206)		Time 2 (N = 200)
	Linear	Nonlinear	Linear	Nonlinear
Transmissionist
Cronbach’s α	.86	.88	.88	.92
Revelle’s β	.80	.84	.82	.88
McDonald’s ωh	.70	.74	.80	.88
Facts first
Cronbach’s α	.67	.68	.80	.83
Revelle’s β	.60	.61	.77	.79
McDonald’s ωh	.59	.60	.73	.78
Fixed instructional plan
Cronbach’s α	.77	.79	.76	.80
Revelle’s β	.70	.73	.72	.77
McDonald’s ωh	.65	.70	.71	.74

Comparison between the nonlinear αs and βs revealed moderate differences (range .03–.07), indicating heterogeneity among factor loadings, challenging an assumption of essential tau equivalence. Comparison between the α and ω_h nonlinear coefficients revealed moderate to large differences (range .04–.14); coefficient α had the larger value in every case. These discrepancies indicate the presence of microstructures within the scales, so coefficient α should be interpreted as an overestimate of the true reliability. Nevertheless, the nonlinear ω_h exceeded the conventional minimum threshold of .7, except for the one scale and at one time point noted above. Accordingly, as demonstrated by Gustafsson and Åberg-Bengtsson (2010), high values of ω_h indicate that composite scores can be interpreted as reflecting a single, common source of variance in spite of evidence of within-scale multidimensionality. The relation among the coefficients was ω_h ≤ β < α in every case. In cases where ω_h = β or ω_h ≈ β, the equality of loadings on the general factor was supported.

3.7. Phase 6: longitudinal measurement and structural invariance

In the sixth phase of the investigation, we inspected measurement and structural aspects of longitudinal invariance, including invariance of factor loadings, item thresholds, residual variances, factor variances, factor covariances, and factor means. Analyses demonstrated full measurement invariance and partial structural invariance. Table 4 presents the results of the succession of parameter constraints conducted to examine potential decreases in fit resulting from the imposing of invariance constraints between Time 1 and Time 2.

Table 4. Tests of longitudinal measurement and structural invariance

Model	χ^2 (df)	∆χ^2 (∆df)	∆χ^2 p	RMSEA	∆RMSEA	CFI	∆CFI
Configural baseline	1065.12 (783)			.058		.926
Full factor loading invariance	1058.03 (801)	27.50 (18)	.070	.055	–.003	.932	.006
Full item threshold invariance	1120.06 (867)	66.25 (66)	.468	.052	–.003	.933	.001
Residual variance baseline	1117.48 (846)			.055		.928
Full residual variance invariance	1120.06 (867)	30.07 (21)	.091	.052	–.003	.933	.005
Full factor variance invariance	1142.52 (870)	18.85 (3)	< .001	.054	.002	.928	–.005
Partial factor variance invariance	1120.38 (869)	2.25 (2)	.325	.052	.000	.934	.006
Full factor covariance invariance	1118.65 (878)	11.24 (9)	.260	.051	–.001	.937	.003
Full factor mean invariance	1120.73 (881)	3.25 (3)	.355	.051	.000	.937	.000

Note. N = 106. RMSEA = root mean square error of approximation. CFI = comparative fit index. The ∆χ² and ∆df are computed from the derivatives from the H₀ and H₁ analyses and is not simply the difference in values between the nested models being compared.

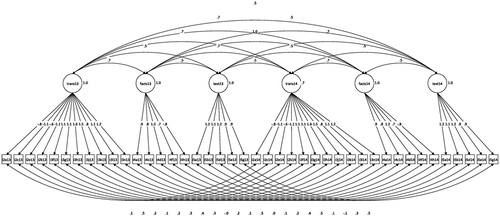
Fit indices for the baseline longitudinal model indicated reasonable fit, suggesting its configural invariance across time: χ2 (783) = 1065.12, p < .001; RMSEA = .058, 90% CI [.047, .058]; CFI = .926; and TLI = .918. Using chi-square difference tests, we found the loadings, thresholds, and residual variances to be invariant across time, with test statistics of DIFFTEST (18) = 27.50, p = .070, for the loadings; DIFFTEST (66) = 66.25, p = .468, for the thresholds; and DIFFTEST (21) = 30.07, p = .091, for the residual variances. These finding were corroborated by means of Chen’s (2007) cutoffs for changes in fit statistics, where corresponding ΔRMSEA and ΔCFI were < .010 and >–.005, respectively, for all tests of loading, threshold, and residual variance invariance. With regard to structural invariance, the constraint of factor variances across time did result in a significant reduction in fit, DIFFTEST (3) = 18.85, p < .001. Modification indices suggested localized strain for the Transmissionist factor, with parameter estimates from the unconstrained model indicating that variance was less at Time 2 than at Time 1 for the Transmissionist factor. We established partial factor variance invariance by constraining the variances for the Facts First and Fixed Instructional Plan factors but allowing the variance for the Transmissionist factor to be freely estimated across time: DIFFTEST (2) = 2.25, p = .325. Notwithstanding factor variances being only partially invariant, the structural invariance of the model was supported by findings of full invariances of the factor covariances, DIFFTEST (9) = 11.24, p = .260, and full invariances of the factor means, DIFFTEST (3) = 3.25, p = .355. Figure 1 displays the diagram for the B-MTL longitudinal measurement and structural invariance model with unstandardized parameter estimates presented.

Figure 1. Beliefs about mathematics teaching and learning longitudinal measurement and structural invariance model with unstandardized parameter estimates.

4. Discussion

Our aim was to clarify the constructs for mathematics-specific, epistemological beliefs that are likely to drive teachers’ instructional decisions. This focus guided us to identify theories involving competing views or priorities concerning the mathematics teaching and learning process. The factorial validity of the B-MTL questionnaire was supported by the results of our model-comparison analyses, intended to ensure that the measurement model was no more complex than empirically warranted. The final model, a three-factor solution, had reasonable fit at both time points, supporting the configural invariance of the model across time. At both time points, all items appeared salient to their respective latent traits. No localized areas of strain were found to be present across time points.

Given our immediate objective to develop a measure to be used in the evaluation of a particular professional-development program, we investigated for the presence of and subsequently removed any items with bias associated with treatment condition. The resulting metric invariance between intervention conditions indicated that the items were related to the latent factor equivalently across groups—ensuring the same latent factors are being measured in each group is a minimum criterion for valid comparisons between groups.

Similarly, our inspection of invariance across time indicated not only metric longitudinal invariance but also scalar longitudinal invariance (invariance of thresholds). The substantiation of scalar invariance indicated that items had the same expected response at the same absolute level of the trait, meaning the observed differences in the proportion of responses at each time point was due to factor mean differences only. Further, we found the model to have full residual variance longitudinal invariance, indicating that the amount of item variance not accounted for by the factor was the same across time. Meredith (1993) used the term strict factorial invariance to describe an instrument that had metric, scalar, and residual variance invariances. Having strict factorial invariance across time indicates that comparisons across time of differences between pre- and post-intervention tests could be considered fair and equitable estimates of change. In addition, the partial invariance of factor variances held, as did the full invariance of the factor covariances and factor means. Because the longitudinal invariance analyses were conducted on the control-group data only, these results indicate that the constructs as measured by the B-MTL questionnaire have stable means and distributions across time.³

As part of the development of the B-MTL questionnaire, we conducted cognitive interviews on a pilot sample of teachers who were not involved in the field test of the questionnaire. The primary aim of the cognitive interviews was to ensure that respondents understood the prompts and response options as intended. Problematic items were subsequently removed or revised. We think this procedure resulted in an important reduction of construct-irrelevant variance in the response data.

Our evaluation of scale reliability revealed several interesting properties of the questionnaire scales. First, comparison of linear and nonlinear forms of coefficient α revealed only small discrepancies, suggesting a tenable assumption of continuity with these data despite their being produced by Likert-type response categories. Second, comparison of coefficients α, β, and ω_h suggested the presence of heterogeneity in factor loadings and within-scale multidimensionality, indicating that coefficient α may be an overestimate of the true scale reliability for these data. Nevertheless, even the lower-bound coefficients generally met conventional thresholds for acceptable reliability. Further, even where within-scale multidimensionality was suggested, the presence of a single common source of variance and the equality of loadings on the general factor was frequently supported.

Notwithstanding the requirements for unidimensionality inherent in some measurement models, Reise, Moore, and Haviland (2010) question the soundness of holding unidimensionality as a measurement ideal, noting that, to achieve a unidimensional model, “one essentially has to write a set of items with very narrow conceptual bandwidth (i.e., the same item written over and over in slightly different ways), which results in poor predictive power or theoretical usefulness” (p. 557). Streiner (2003) argued a similar point, noting “αs over .90 most likely indicate unnecessary redundancy rather than a desirable level of internal consistency” (p. 103). Understanding that some lumpiness should be expected, particularly for data drawn from measures of complex psychological processes, we believe the range of moderately sized reliability coefficients estimated for the sample is suitable, given the nature of the constructs.

4.1. Limitations

Given the self-report feature of the B-MTL questionnaire, the extent to which the teachers’ report is consistent with actual behavior is not yet known. Some findings indicate that teachers’ self-report data in similar domains can be consistent with observer data (Mayer, 1999; Ross, McDougall, Hogaboam-Gray, & LeSage, 2003). Additional work is warranted to determine whether teachers’ behaviors are consistent with their reported beliefs and to explore relations among teachers’ reported beliefs and student learning in mathematics.

We view the Fixed Instructional Plan scale as a belief that is created and shaped by practical problems encountered in the practice of teaching and working in school organizations. That is, although it may be measuring a belief among teachers that the sequence in the book reflects the sequence that students must learn, this particular scale is probably measuring a belief that is influenced by a more complex set of factors than, say, that of the Transmissionist scale. For example, teachers may score high on the Fixed Instructional Plan scale for a variety of reasons, including beliefs about the role of the teacher in carrying out the plan of the larger school organization, which may include perceptions of pressure from principals, parents, or other teachers. These contextual factors have a strong influence on the interactions among teachers’ knowledge, beliefs, and instructional practice in the theoretical model proposed by Ernest (1989). Other reasons for adhering to the scope and sequence prescribed in a textbook might be low teacher confidence in the subject area or limited efficacy with deviating from the textbook in a way that will result in a better outcome. Therefore, although the Fixed Instructional Plan scale intends to measure the extent to which teachers believe that they should either adhere closely to the scope and sequence in the mathematics textbook or make adaptations to it, we recognize that the construct underlying teachers’ responses is probably multifaceted, comprising sources of variation that are context and situation dependent. Should further investigation demonstrate the Fixed Instructional Plan factor to be predictive of student achievement or otherwise an important moderating factor, further scale development would be warranted to allow these dependencies in the data to be studied and better understood.

Further, we note that the Fixed Instructional Plan construct may require respecification as curricula advance technologically and adaptive functionality becomes more prevalent. To the extent that the construct proves to merit further inquiry, we anticipate its operationalization will need to undergo some drift in accordance with the evolving nature of how students interact with content and curricula.

Another potential limitation is the subtle connotation of language. Researchers using the questionnaire with teachers in future policy environments, in other parts of the United States, or in other English-speaking countries where the same words may be used differently, or researchers translating the B-MTL to languages other than English must carefully consider the word choice in order to avoid the potential influence of terms or ideas that may influence teachers to respond in socially preferred ways.

4.2. Future directions

Valuable future work investigating concurrent or discriminant validity may include a comparison of data gathered through this instrument and that from other existing instruments attempting to measure teachers’ pedagogical content beliefs, such as the questionnaires developed by Peterson et al. (1989), Staub and Stern (2002), or Campbell et al. (2014). Before the respecification of the set of items in the Facts First scale, the working name for the construct was Incremental Mastery. We suspect that the Facts First scale and the Mastery orientation described by Campbell, Clark, and colleagues (Campbell et al., 2014; Clark et al., 2014) may be converging to a similar belief construct. The work of Campbell et al. (2014) and Clark et al. (2014) was not known to us until after the second wave of field-testing of the B-MTL questionnaire, but we think their Mastery orientation scale could be used to investigate concurrent validity or to further clarify the underlying construct being measured by these items.

The B-MTL questionnaire does not attempt to measure teacher beliefs about the nature mathematics directly. Thompson (1992) stated a clear opinion that beliefs about the nature of mathematics probably undergird all other beliefs about mathematics teaching and learning. We made some attempt to write items designed to measure teachers’ beliefs about the nature of mathematics, but we were not confident in them after conducting the cognitive interviews. With respect to beliefs about the nature of mathematics, the Facts First orientation and the Fixed Instructional Plan orientation both seem to be consistent with a view that mathematics instruction should be sequenced according to a hierarchy based upon logical assumptions about the structure of the subject matter (Ernest, 1989; Thompson, 1992). For an interesting discussion and conceptual framework on the topic of the nature of mathematics, we recommend Ernest (1991). An important future direction for this work may be to see how teachers’ views about the nature of mathematics might be associated with their beliefs about teaching and learning of mathematics.

There is considerable work to be done to support the validity argument for the B-MTL. We encourage prospective users of the questions and scales in the B-MTL to explore their use in combination with other extent and not-yet-developed measures for further development, refinement, and validation. If the interplay between teachers’ knowledge, beliefs, and instructional practice can be better understood, future efforts to improve teaching and learning may be more productive (Bray, 2011; Fennema & Franke, 1992)

In its current form, the B-MTL questionnaire can measure three facets of beliefs about teaching and learning of mathematics. We don’t set any expectation the B-MTL must be used in its entire form. We hope to grow the scope of the questionnaire over time and use it in combination with other measures so that it can be more inclusive and can encompass other clearly defined facets of beliefs.

Some scholars have argued that the types of beliefs we identify here are durable and more resistant to change than other facets of beliefs, such as attitudes (Jong et al., 2015; Thompson, 1992). We remain agnostic and open to the possibility that these beliefs are malleable. Directions for future work will include tests of the effect of interventions such as CGI-based professional-development programs designed to affect these aspects of teacher beliefs about mathematics teaching and learning. Ernest (1989) acknowledged that teachers in the same school have similar instructional practice, and the structure of the organization may supersede their individual beliefs with respect to the effect on their instructional behaviors. Any future studies using the Fixed Instructional Plan scale should consider the intraclass correlation of teachers and account for the nested structure of the data if they include multiple teachers from the same school building.

4.3. Conclusions

At this time, the B-MTL questionnaire provides a refined, efficient way to measure where a teacher falls on the spectrum of transmissionist and constructivist views of teaching and learning. The B-MTL questionnaire also comprises a tool to measure two constructs that are new to the literature on pedagogical content beliefs in mathematics: facts first, and fixed instructional plan. These constructs represent only part of the full scope of teacher beliefs, and more work is needed in order to map the landscape of teacher beliefs about mathematics teaching and learning and to provide further validation of the questionnaire and the constructs.

The iterative procedure we followed to evaluate and respecify the B-MTL questionnaire resulted in a structurally valid measurement model that (a) was free of moderate to large differential item functioning associated with treatment status, (b) had full measurement invariance and partial structural invariance across time, and (c) had scales that were reliable for the current sample. The resulting questionnaire appears to demonstrate sufficient validity and reliability to meet standards in educational and psychological measurement.

As many scholars working in the field of teacher beliefs before us have argued (e.g., Adler et al., 2005; Philipp, 2007; Wilkins, 2008), large-scale studies are needed to test and further establish theories about the relations among teacher beliefs, instructional practice, and student learning. The relatively short B-MTL questionnaire lends itself to large-scale, empirical study. We therefore hope the B-MTL will permit further implementation of large-scale empirical tests of the theorized relations among teacher beliefs, knowledge of subject matter, instructional practice, and student learning.

Acknowledgements

The research reported here was supported by the Institute of Education Sciences, U.S. Department of Education, through Grant# R305A120781 to Florida State University. The opinions expressed are those of the authors and do not represent views of the Institute or the U.S. Department of Education. Dr. Lisa Brooks provided valuable assistance in refining questionnaire items and conducting cognitive interviews. Dr. Amanda Tazaz provided valuable assistance in assisting with the consent process and data collection.

Additional information

Funding

This work was supported by the Institute of Education Sciences [R305A120781].

Notes on contributors

Robert C. Schoen

Robert C. Schoen (https://www.schoenresearch.com/) conducts research driven by a single question, what will it take to improve mathematics teaching and learning for all students? Much of his work focuses on the influence teachers have on their students. Schoen and LaVenia have collaborated on the design and implementation of more than a half-dozen, large-scale, randomized-controlled trials of mathematics professional-development interventions. These programs employ a variety of promising approaches, including formative assessment, lesson study, professional learning communities, and cognitively guided instruction. To date, the Beliefs about Mathematics Teaching and Learning (B-MTL) questionnaire has been used in four randomized trials. The B-MTL questionnaire has detected large and statistically significant effects of Cognitively Guided Instruction and the Thinking Mathematics programs on teachers’ self-reported beliefs.

Notes

1. The Clark et al. (2014) questionnaire had not yet been published at the time we were doing this work, and we were not yet aware of it.

2. Time 1 (N = 206) with school fixed effects: χ2(564) = 521.595, p = .899; RMSEA = .000; 90% CI [.000, .011]; CFI = 1.000; and TLI = 1.215. Time 2 (N = 200) with school fixed effects: χ2(564) = 586.344, p = .249; RMSEA = .014; 90% CI [.000, .027]; CFI = .978; and TLI = .974.

3. Control group model-based correlations between Time 1 and Time 2, indicating the 9-month-lag test-retest reliability of the scales, were r = .88, p < .001 (Transmissionist); r = 1.00, p < .001 (Facts First); and r = .72, p < .001 (Fixed Instructional Plan).

Table

			Standardized loading (SE)
Item	Order	Beliefs about mathematics teaching and learning questionnaire items by subscale	Time 1	Time 2
Transmissionist
2a.	48	Effective math teachers consistently create opportunities for students to solve problems in their own ways before the teacher has already shown them a good way to solve that type of problem.	–.76 (.03)	–.68 (.04)
2c.	19	Before showing students how to solve math problems, teachers should encourage students to create their own ways to solve them.	–.71 (.04)	–.76 (.03)
2e.	46	It is very important for students to discover how to solve math problems in their own ways.	–.61 (.05)	–.61 (.04)
2k.	28	Students can figure out ways to solve many math problems prior to formal instruction.	–.62 (.05)	–.79 (.03)
3f.	25	The teacher should demonstrate how to solve word problems before students are expected to solve word problems on their own.	.65 (.05)	.80 (.03)
3g.	6	Most students cannot figure out how to solve math problems by themselves and must be explicitly taught.	.60 (.05)	.68 (.04)
3h.	8	Asking students to solve problems in their own way causes too much frustration.	.74 (.04)	.67 (.04)
3j.	52	Allowing students to develop their own strategies for solving math problems creates too much risk that students will learn to solve problems incorrectly.	.88 (.03)	.72 (.03)
3k.	38	Students should be instructed to solve problems the way the teacher has taught them.	.61 (.05)	.76 (.04)
3l.	42	Teachers should not focus too much on expecting students to solve problems in their own way, because that leads to student frustration.	.69 (.04)	.83 (.03)
3n.	50	It is more effective to show students how to solve problems than to let them solve problems in their own way.	.78 (.03)	.78 (.03)
Facts first
4a.	1	Students should master some basic facts before they are expected to solve word problems.	.53 (.07)	.77 (.04)
4c.	39	Students should master carrying out computational procedures before they are expected to understand why those procedures work.	.60 (.06)	.69 (.04)
4d.	44	Students must know the basic facts before they can understand the meaning of the four operations (addition, subtraction, multiplication, and division).	.65 (.06)	.82 (.03)
4f.	51	The ideal way to teach problem solving is to have a student repeatedly solve one kind of problem at a time until he or she has mastered that type of problem.	.67 (.05)	.68 (.05)
4h.	13	Even students who have not learned the basic facts can have efficient methods for solving word problems.	–.58 (.07)	–.79 (.03)
Fixed instructional plan
5a.	30	If the teacher deviates from the sequence in the textbook, students will not learn the mathematics they are supposed to learn.	.75 (.05)	.84 (.04)
5b.	27	Following the textbook closely ensures that the teacher is focused on the right sequence of mathematical topics.	.77 (.04)	.75 (.04)
5d.	20	It is important to follow the textbook and/or pacing guide with fidelity, even if it seems that students do not yet understand a mathematical concept.	.75 (.05)	.65 (.06)
5e.	32	If the scope and sequence in the math textbook is followed carefully, most students will eventually understand the mathematics they are supposed to learn.	.70 (.05)	.56 (.06)
5g.	35	Teachers should follow the sequence in the textbook rather than sequence instruction on their own.	.63 (.05)	.72 (.05)

Note. Time 1 N = 206. Time 2 N = 200. Order indicates the order presented on the original 55-item questionnaire. Standardized factor loadings are based on models with the scaling set by fixing the variance for each factor to 1.

Appendix B

Table

	Model specification
Test of invariance	Less restrictive model	Analysis model
Factor loadings	Factor loadings all estimated Item thresholds all free Item residual variances all fixed = 1 Factor variances all fixed = 1 Factor covariances all free Factor means all fixed = 0	Factor loadings held equal across time Item thresholds all free Item residual variances all fixed = 1 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free Factor means all fixed = 0
Item thresholds	Factor loadings held equal across time Item thresholds all free Item residual variances all fixed = 1 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free; Factor means all fixed = 0	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2
Residual variances	Factor loadings held equal across time Item thresholds held equal across time Item residual variances fixed = 1 at Time 1 and free at Time 2 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2
Factor variances	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances fixed = 1 at Time 1 and free at Time 2 Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances all fixed = 1; Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2
Factor covariances	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances all fixed = 1 Factor covariances all free Factor means fixed = 0 at Time 1 and free at Time 2	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances all fixed = 1 Factor covariances held equal across time Factor means fixed = 0 at Time 1 and free at Time 2
Factor means	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances all fixed = 1 Factor covariances held equal across time Factor means fixed = 0 at Time 1 and free at Time 2	Factor loadings held equal across time Item thresholds held equal across time Item residual variances all fixed = 1 Factor variances all fixed = 1 Factor covariances held equal across time Factor means all fixed = 0