WATER ACTIVITY AND ITS PREDICTION: A REVIEW

Abstract

Water activity is a very useful parameter in food preservation. Raoult's law gave a first base in the case of ideal solutions. In 1966, Norrish presented a thermodynamically based equation to predict activity coefficients in confectionery syrups. Later, the Gibbs-Duhem equation was used to produce series of predictive models starting with Ross in 1975. Some apparent refinements have been proposed since then by Caurie, followed by Lilley and Sutton. In this work an analysis of different approaches are discussed with their limits. New directions are also suggested for either a more numerical approach to solve directly the Gibbs-Duhem equation, or a more empirical one, based on the zonotopes.

INTRODUCTION

In food science, water activity is very useful as a measure of the potential reactivity of water molecules with solutes. It is indeed very important to know the characteristics of a solution involving various components. Unfortunately, it is neither easy to measure nor to calculate them. In practice one can only determine easily the activity of binary solutions. More complex solutions involving interactions between different components and modification of water behavior are unfortunately not so straightforward. A first attempt is done using Raoult's law for ideal solutions. Caurie (1983) did try to modify this equation but only to obtain an apparent better model. Unfortunately, ideal conditions of liquid solutions are less often encountered compared with gases and Raoult's law rarely can be applied for aqueous solutions. The results obtained are also often deceiving as described by Hawkes (1995). But Chen (1987; 1989) combined this law with the modification by Schwarzberg (1976) to predict water activity for sugar solutions and some liquid foods. Benmergui et al. (1979), Fontan et al. (1979), and Chirife and Fontan (1980) also proposed a model for intermediate moisture food using Bromley's (1973) equation for electrolytes. Those results are rather good but very much restricted to a too specific type of solution. The Gibbs-Duhem approach [Eq. 1] as described by Guggenheim (1977) provides a theoretical background to evaluate the water activity in a general case. Therefore, this equation has been used as a starting point of many interpretations with various degrees of success.

Solving Gibbs-Duhem Equation

The Gibbs-Duhem equation describes the activity of a solution composed by N components of activity {a _i } _{i = 1‥N} in proportion {n _i } _{i = 1‥N} .

If we consider a water solution and the activity given in Equation 2 as a function of molality, m _i and activity coefficients, Y _i ,

Then Equation 1 can be integrated as

Thus, a distribute integration is possible because the molality is not a function of the activity:

But in this system the activity coefficients, Y _i , for any solution are not known from standard tables. Moreover, such an equation is not easy to solve analytically in practice. That is the reason why Ross (1975) started to propose some simplifications to obtain a simple but usable model.

Ross Method

From the Gibbs-Duhem equation Ross (1975) deduced a simple expression of the water activity. There are two main steps in Ross's development:

•	Developing the ln function to its series, and
•	Neglecting the interactions between diluted components

The first part the disturbing neperian logarithm can be expanded through its Taylor development to the first order. This implies that the concentrations of the components should be close to 0 and/or their relative activity to 1. Thus, the simple Equation 4 is obtained in the binary case:

In practice at least ternary solutions are of interest, but the interactions between the different compounds are difficult to evaluate. The second point of Ross' method consists also in the substitution of the relative activities of each component in the specific solution by its standard activity in a binary water solution. In this way it is possible to evaluate separately all the Y _i of the complex multicomponent system, set to Y _i ^o from the binary systems. In practice, the interactions between the different components are neglected to the water activity. Thus, in the only case of multicomponent dilute solutions, the water activity, a _w , can be approximated by Equation 5 as equivalent to the product of the standard binary activity, a _i ^o , of each component:

Limitations of Ross Model

Nevertheless these two simplifications restrict the use of Ross' method to the very dilute solutions where the various interactions are neutralizing each other or are of no importance. It was also observed by Bone et al. (1975) and Chuang and Toledo (1976) that this model overestimates observed values in practice. To correct this effect, Caurie (1985) proposed a modification to make a simpler and finer way to evaluate Gibbs-Duhem equation based on Ross model without such losses. However, the proposed solution seemed to be fragile in the high concentration range. The reason could be an intrinsic nonrigorous argumentation.

CAURIE'S DEVELOPMENT

Gibbs-Duhem

Starting from the Gibbs-Duhem Equation 1, the same path as Ross was followed by Caurie (1985). The activity was substituted by the product of molality and relative activity and the function ln(1 + x). Then it was possible to scatter the whole equation in the case of, for example three components in water.

Neglecting the Interactions

Ross' steps are then followed in replacing Y _i by Y ^o _i . The many terms are then gathered back to their original form by applying the same Equation 4 in the other direction with the standard values. Finally, a complete simplification of all the terms should occur to obtain modified Ross as Equation 6.

Some of those terms in Equation 6 are selectively kept by Caurie to fit more closely to the suspected losses by interactions as suggested by his experiments. A new predictive Equation 7 is thus obtained:

It can be noticed that this equation is of third order whereas the previous steps gave the first order.

The Path Followed

In fact the argument is quite special if the whole scattering and gathering is taken apart. One can consider the definitions of both standard binary and effective activities as:

Thus, substituting the activity coefficients produces the following result for the activity

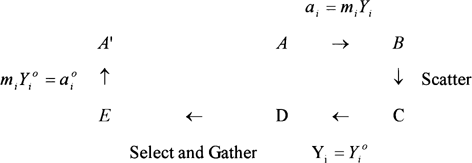
The complete scheme can be summarized as in Fig. 1. From A to E one has a _i = m _i Y _i , which is approximated by a _i ^o = m _i Y ^o _i by simply approximating Y _i by Y _i ^o . Whatever is happening between A and A′ should finish in a succession of terms simplifying one each other except the product described already by Ross. The state A′ is indeed very close to A, but from the selection between D and E Caurie obtained second and third order terms to “correct” the approximation. It appears in fact that those terms are quite arbitrarily chosen to represent the interactions between the solutes. But they definitely do not have any physical meaning. Caurie (1983) has already used the same type of modification to correct Raoult's law. Moreover, in this case those added terms are of a higher order than the initial development approximations. If one develops the neperian logarithm to the second order some additional terms of much more importance should appear in Caurie's final equation. This new Equation 7 is also giving better prediction than Ross [Eq. 5] for the experiments made by Caurie.

Figure 1. Complete scheme of path followed in Caurie's development.

THE MODEL OF LILLEY AND SUTTON

Despite this not mathematically rigorous development by Caurie (1985), it is possible to look for a finer approximation of water activity from the Gibbs-Duhem equation than Ross obtained. Lilley (1987) made a first attempt after pointing out some apparent weakness of Caurie's equation and proposed his own development. He also found some thermodynamic symptoms of the error involved by the approximation by Caurie. Indeed, it looks like the diagnosis of Lilley is not entirely correct either. When both Ross and Caurie integrate Equation 3, they consider the molality as independent of the activity coefficient. But Lilley (1987) denied this fact. However, there is no reason to refuse the independence of the molality to the activity in the integration. Nevertheless the second part of Lilley's criticism, concerning the symptom, corresponds exactly to the thermodynamic interpretation of Caurie selecting half of the added terms. Lilley and Sutton (1991) also proposed to add terms to Ross' equation but based on chemical properties. First they pointed out a series of factors that might be of importance: size differences between solute(s) and solvent, solvent binding, solute interactions, solvation, and volume differences. Then, they used the representation of water activity [Eq. 8] by Robinson and Stokes (1965) as:

The water activity, a _w , is now a function of the osmolality, m _i , the relative molar mass of the solvent, M _w and the molal osmotic coefficient, Φ. The latest can then be approximated with Equation 9 as proposed by McMillan and Mayer (1945) for homotactic interactions.

Φ is also given as function of the osmolality, m _i and the homotactic coefficient, g′ _ii . Then an extension of Equation 9 to heterotactic coefficient leads to a new Equation 10 for the water activity.

As it is possible in this case to deduce the heterotactic term from the binary solutions, a completely empirical Equation 11 for three components systems can be obtained:

In a more general case the homotactic coefficients can be used to only approximate the heterotactic coefficients. Then, the equation that gives water activity does not look so good but it is still efficient and absolutely possible to evaluate. The results presented are once again very close from their experiments performed with multicomponent systems of different types of sugar.

The final model is also the result of a succession of approximations based on the modeling of some chemical properties of the systems and the recombination of experimental data. The stability of such a combination of approximation may also be doubtful but the use of experiments from binary systems is a good factor to reduce the effect of the approximated and/or unknown parameters.

Caurie (1985) was looking for some higher order terms in Ross' solution of the Gibbs-Duhem equation. He tried to base his work on a mathematical development of the equation. But at one point he arbitrarily picked up some of the positive terms and neglected the others. Thus, he obtained a better prediction to his experimental data but without any real mathematical or physical meaning. He would have obtained even better results by using spline or interpolation. The mathematical validity of his added terms would then have been clearer even if they would still be without any physical meaning.

Lilley and Sutton (1991) did really try to generate higher order terms from the chemical/physical properties of the system. Their model is also likely to work for a broader range of combinations. The weak point is nevertheless the use of a succession of approximation models. The validity must also be restricted to the intersection of all validity domains and any type of extrapolation should be taken with extreme care. The introduction of some empirical values tends to reduce the restricting effect by taking into account some unknown phenomena. Those two different approaches are mixing mathematical modeling and experimental data without any clear limit. Nevertheless, it must be possible to go for either a real numerical model or one based on experimentation.

The absence of any analytical solution to the Gibbs-Duhem equation is the source of most of the approximation models. No matter how far the analysis can lead us, scientists always need to achieve numerical values sooner or later. It should also be possible to solve the equation numerically from the beginning by successive approximations. Nowadays, computers and numerical science can provide many tools to find a reasonable solution. And this could be applied regardless of the number of components in the system. Moreover, such an approach can combine many models to fit more closely to reality. Thus, the integration of a high number of phenomena would not be a real problem from the calculation point of view. The only problem is feeding the calculator good model equations. On the opposite side, the empirical method takes everything into account as far as the described properties are known without really looking for an ideal, exact explanation.

The best way to take into account all the phenomena involved in a reacting system is to use experimental data. Such data must in fact be the projection of all the characteristics of the system. The prediction will be close to reality if more directions of projection (properties) are used. Even if the exact interactions between all the characteristics are not known they will be automatically integrated into the model. Moreover, a large amount of measurements will avoid the noise induced by any experimental result. The experiments provide a huge amount of data full of hidden information. The actual tendency is to use a statistical approach to get results. But this does not really lead to any model. It would be more interesting to use what has been specifically designed to solve mixing problems: zonotopes. This relatively new mathematical field comes from the Separation Theory (Lacolle et al., 1994). In the vector space of chemical products, solutions are represented by vectors and their mixture by a vectorial sum (Girard et al., 1989). A vectorial reconstruction of Minkowski sums, the zonotopes, provides information on the solution properties. It has already been used for chromatography (Valentin, 1991) and feasibility studies of several mixtures (Lacolle et al., 1993). It does provide exact mathematical tools to reach very good approximation based on a standard binary solution for many different components.

CONCLUSIONS

The tentative to improve Ross'(1975) approximation of water activity is full of the temptation to add higher order terms. Caurie (1985) did try to use a mathematical approach but just picked up some terms with neither a mathematical nor physical reason. His model was reported to have only some satisfactory applications in the food domain. Lilley and Sutton (1991) looked for mathematical approximations of physical phenomena likely to occur in the multicomponent system. They also obtained good results but the use of this model must be restricted to the domain where all the approximations used apply; however, the introduction of experimental data tend to relax this limiting effect. The use of either a complete numerical or empirical model should produce more reliable and widely applicable predictions. The first one could be based on a numerical solution of the Gibbs-Duhem equation where the analytical approximation failed. The latest one could be obtained by applying the mathematical tools provided from the separation theory for mixing to predict water activity of multicomponent systems from binary solutions' experimental data.

Acknowledgments