Young students’ meaning-making when working with mathematics textbooks – A multimodal study focusing on the designed and the discovered

ABSTRACT

This article focuses on students' meaning-making when working with mathematics textbooks from a multimodal approach that encompasses all resources for communication, which is an under researched area. Central to this study are the designed meanings of the textbooks and the affordances discovered by students when working with the textbooks. Video transcripts from 18 Year 1 (ages 7–8) students working with seven textbook pages were analysed. The results show that the designs of exercises are complex, that the students use different approaches when working with the textbook – from one exercise to another as well as within the same exercise – and that they sometimes discover content other than what the textbook was designed to offer. Conclusions drawn from this are that textbooks can be improved as learning tools – multimodal aspects of this are highlighted – and that more awareness of multimodality in mathematics teaching could support students' mathematical learning.

KEYWORDS:

• Meaning-making
• design
• affordance

Introduction

Mathematics textbooks are common learning tools used by more than 75% of students in compulsory schools worldwide (Mullis, Martin, Foy, & Arora, 2012). Textbooks are designed to offer specific content, and working with them involves interpreting that content. Little is known about how students perceive this process in terms of the meaning they make and the way this meaning-making affects their learning. Meaning-making is understood as a creative act in which individuals seek to understand their environment (Kress, 2010; Selander & Kress, 2010). With more knowledge about students’ meaning-making when working with mathematics textbooks, mathematics education could be developed to provide more efficient learning situations that, by extension, support students in their mathematics learning.

Mathematics is a multimodal subject (O’Halloran, 2005), which means that different resources for communication, or modes (see, for example, Kress, 2016), is essential in doing and expressing mathematics. Multimodality emphasises the fact that communication takes place through several modes, such as images, writing, mathematical symbols and speech (Kress, 2010), and meaning-making can be conceived as activities in which learners understand their environment (Kress, 2010). A multimodal approach can be used to render rational descriptions of mathematical representations and interpret the function of represen­tations (Morgan, 2006). These representations may consist of a graph, an image, or the display of a number by using the fingers, etc. This approach provides more versatile tools for understanding how students work with textbooks, as all resources for communication – or modes – are taken into account. It also helps understand all the textbook’s different resources, which contributes to a deeper understanding of the textbook as a learning tool. This multimodal study recognises the importance of considering all modes (cf. Kress, 2016) – when studying students working with mathematics textbooks. Students’ work is used in this study to emphasise the fact that meaning-making involves active action.

In two recent studies, the textbook as a multimodal learning tool was studied (Norberg, 2019, 2021). The results showed significant differences between different Swedish Year 1 textbook series as to their mathematical content as well as the modes used for communication, and that different textbook series require different types of reading. The results also showed that the design sometimes makes it possible to solve an exercise without focusing on the exercise’s mathematical content. This indicates that mathematics textbooks are complex and challenging to read (cf., Dyrvold, 2016; Segerby, 2017) and demonstrates the value of this study.

Students’ individual work with mathematics textbooks is a virtually unexplored research field (e.g. Österholm & Bergqvist, 2013; Rezat & Straesser, 2014; Shepherd, Selden, & Selden, 2012). Research on teachers’ use of mathematics textbooks exists (e.g. Haggarty & Pepin, 2002; Remillard, 2005), but studies on students’ use of textbooks is limited (Fan, Zhu, & Miao, 2013; Rezat, 2008), and even more the youngest students. Studies focusing on a multimodal approach in which different modes are highlighted are even less common. So, this study complements existing research on students’ work with mathematics textbooks and provides new knowledge regarding a multimodal approach to mathematics textbooks.

A mathematics textbook has an aim, and is designed to offer a specific content – a designed meaning (concept based on Selander & Kress, 2010). The designed meaning is defined as the author’s or producer’s purpose with the exercise. A designed meaning is not the same as the affordance a student actually discovers when working with the textbook. Therefore, it is relevant to compare what the exercises are designed to provide with the meanings that students make. Central to this study are thereby the textbooks’ designed meanings compared with affordances discovered by the students; in short, the designed and the discovered. This means that what is studied is not the mathematics teaching itself, but rather situations that involve students’ individual interactions with the textbook. Notwithstanding how much the teacher plans and teaches, it is also necessary that the student is able to make meaning when working alone with the mathematics textbook. That is the content of this study.

This study emerged from the challenge of supporting students’ individual interaction with mathematics textbooks, which, by extension, supports their mathematics learning. The aim of the study is to understand how students in Swedish Year 1 make meaning when working with mathematics textbooks, focusing specifically on subtraction. The analysis has been guided by the following research questions: “What meanings are the textbooks designed to offer?” and “What affordances do the students discover when working with their textbooks?” A comparison between the designed and the discovered is made. This study contributes to research on students’ work with mathematics textbooks. If more is known about how students make meaning when working with mathematics textbooks, this may evolve to permit better learning situations, which will allow students’ mathematical learning to increase.

Previous research on students working with mathematics textbooks

The literature search showed few studies on students’ working with mathematics textbooks. Of the studies that have been carried out, there is a research area focusing on language, reading and writing. Österholm (2008) studied 195 upper-secondary school and university students reading mathematical textbooks. He concluded that students develop reading strategies that do not support the learning of the mathematical content, and can thereby be understood as reading that should be avoided. Shepherd et al. (2012) studied 11 undergraduate students; even though they were all considered competent readers, they struggled to read the mathematics textbook. Also, Berger (2017) studied reading focusing on two adult students. She concluded that “mathematics textbooks suffer a double, possibly linked, ignominy: they are under-used as a learning resource and they are under-researched in terms of how they can be read productively by learners” (403). She emphasised the need for further research. Focusing on writing, Powell, Driver, Roberts, and Fall (2017) stated that both general vocabulary and mathematics computation measures are significant predictors of mathematics vocabulary, in a quantitative study of 193 students (aged 8–11). Amiripour, Dossey, and Shahvarani (2017) studied writing and symbols in word problems in four classes (aged 9–11), before and after tests. In this comparative study, students demonstrated a strong emphasis on mathematical symbols. One consequence of this is that it may lead to an approach where students decode mathematical symbols as the essential part of a mathematics task.

All these studies focus on language, but based on a more traditional view of language specifically linked to reading and writing text. One study also focused on mathematical symbols, but none of them included images and other visual expressions in mathematics. As mathematics is a multimodal subject, studies like these do not consider all modes for communication and thereby miss essential parts of the communication in mathematics teaching.

Some studies focusing on all modes in the textbook (writing, images, and mathematical symbols) were found in the search. One was conducted by Rezat (2008), though not using a specifically multimodal approach. He asked 74 secondary school students (aged 11–12/17–18) to highlight the sections they used and number the order they made use of them, after working with textbook exercises. He found that students used the textbook in five different activities: for solving tasks and problems, to look something up, for practising, when performing follow-up coursework, and in anticipation. The result also showed that students rely heavily on worked examples. Another study focusing on all modes but not from a multimodal approach was Shumway et al. (2016). In a comparative study, using both quantitative and qualitative analysis, responses and strategies to open-response fraction items from 355 students (aged 8–10) were analysed. Shumway et al. (2016) concluded that instruction in virtual manipulative representations, physical manipulatives and textbook representations are all important.

In a study aiming to develop a framework for analysing multimodal interaction, Alshwaikh (2011) used a multimodal social semiotic approach to study students (aged 13–14) from the UK and Palestine working with diagrams. He stated that a multimodal approach to representation and communication provided a more detailed picture of how students make meaning when working with mathematics. Two Swedish studies focusing on multimodality are Segerby (2017) and Dyrvold (2016). Segerby (2017) studied students (aged 10–11) reading textbooks. The results showed that students needed to develop strategies and writing proficiency when working with textbooks. Segerby concluded that mathematics textbooks are challenging to read, and that one reason for this is their multimodal complexity. Dyrvold (2016) did not study textbooks, but students (aged 15–16) reading mathematical tasks from the Programme for International Student Assessment (PISA) and national mathematics tests. The results showed that the tasks were difficult for students to read, and that this was connected with combinations of modes that include images. Both Dyrvold (2016) and Segerby (2017) concluded that textbooks are difficult to read and that modes are related to this difficulty.

Altogether, it can be stated that working with mathematics textbooks is complex, and the research field is under-researched especially concerning the youngest students. A multimodal approach would complement existing research as it can contribute to the research field, with a broader perspective on textbooks and students’ mathematical learning. The already existing multimodal studies state that this perspective provides a more detailed picture of students’ meaning-making (Alshwaikh, 2011), that the variety of modes play a part in this (Segerby, 2017) and is connected with combinations of modes that include images (Dyrvold, 2016). But there is no knowledge of how students use different modes and if the designed meanings are the affordances students discover in their meaning-making. There are also no implications for how teaching can be developed according to multimodal aspects. So, the research gap lies both in research on younger students and textbooks, and on a multimodal perspective that highlights all modes used for communicating mathematics.

Conceptual framework

The conceptual framework is grounded in a multimodal design theoretical approach (Selander & Kress, 2010), which draws from the social semiotics field (cf. Kress, 2010), where meaning-making is essential. Meaning-making can be understood as an activity where the individual seeks to understand the outside world, and also as something that is happening constantly, everywhere, and in a social and cultural context (e.g. Kress, 2010; Selander & Kress, 2010). A multimodal perspective refers to the assumption that all communication takes place through various modes, such as images, gestures, speech and writing (Kress & van Leeuwen, 2001). O’Halloran (2005) describes mathematics as multimodal in nature, because learning mathematics involves making meaning using different modes. Modes are resources for meaning-making (Kress, 2016). All modes are resources that have advantages and limitations, and according to this approach, different modes cannot offer the exact same meaning. To fully understand textbooks, for example, all modes must be considered (Bezemer & Kress, 2010). In this study, multimodality is used both according to the different modes in the textbooks: images, writing, and mathematical symbols; and to students’ meaning-making: speech, body language, images, writing and mathematical symbols.

Meaning-making: the writer and the reader

Meaning-making is defined as a creative act, in which the individual makes meaning of their environment (Kress, 2010; Selander & Kress, 2010). Meaning-making occurs continuously and describes the process in which the individual, with the help of representations, understands their surroundings. An example may be a student’s work with their textbook. The individual’s meaning-making in their encounter with the textbook can never be an exact replica of the textbook author’s meaning-making of the same (Bezemer & Kress, 2010). The student’s meaning-making is always new.

Morgan (2001) writes about the relationship between writers and readers. She claims that, as all communication involves interpretation, and thus always a certain amount of disagreement between the way that writers and readers understand the text, it is more difficult to communicate through text than it is face-to-face. The writer’s role is to both write and read, while the reader’s role is merely to read (Kress & van Leeuwen, 2006). Kress and van Leeuwen further describe the relationship between writer and reader in terms of the writer being invisible to the reader and vice versa. This means that the writer must create what Eco (1984) calls a model reader – the ideal reader – to keep in mind when creating the text. The analysis of the textbook pages in this study derives from this concept and is referred to as the designed meaning, described under the next heading. This concerns both the operations of arithmetic (subtraction) that the exercises address as well as other central content deriving from curriculum goals. Meaning is made by both writer and reader. First, the writer’s meaning is made, and this is interpreted in the reader’s meaning-making. The reader’s meaning, however, is never the same as the writer’s, as “messages are encoded, transferred and then decoded” (Bezemer & Kress, 2010, p. 13).

The design of mathematics textbooks

The concept of design concerns the way learning tools are designed and how individuals are involved in designing their learning situations (Selander & Kress, 2010). Design involves the formation of both objects and conditions for communication, and design is understood as a communicative process in which the individual, through involvement, depicts representations (Selander & Kress, 2010). This process may involve, for example, the design of textbooks. In society, there has been a shift in the relation between writer and reader, according to Bezemer and Kress (2010). In some textbooks, including longer narratives, most of the work is done by the writer, while in others, more responsibility is given to the reader (Bezemer & Kress, 2010). Mathematics textbooks for the early school years belong to this second category. In the past, there was a focus on writing in order to understand the text; now, all modes used must be included.

Based on the above, this study investigates the design of the mathematics textbook exercises, with a special focus on the different modes involved. The concept of design is used in line with the idea that mathematics textbooks are designed learning tools and how this bears on the content the exercises are designed to offer. This is related to the students’ meaning-making when working with the exercises.

Designed meaning and affordance

The concepts of designed meaning and affordance are used in order to understand students’ meaning-making when working with textbooks. Designed meaning (Selander & Kress, 2010) describes the meanings that exercises are designed to offer, according to the teacher’s guide, or the meanings needed in order to learn specific mathematical content designed into the mathematics exercise.

Affordance is used according to those that students discover. Affordance is linked to the tool and the potential meaning that can be created (Gibson, 1986). Danielsson and Selander (2016) describe affordance as offered meaning potential, or as opportunities and limitations, and answers the question “What is offered in the situation?”. The relational view implies that an affordance exists only in the meeting between the individual and the tool. There may be more affordances given for an individual’s meeting with a tool, but different individuals can also discover different affordances (Selander & Kress, 2010). Selander and Kress (2010) write that, within the concept of affordance, there always exists still undiscovered potential meanings awaiting discovery. Jewitt (2016) writes that, in multimodal research, affordance is a controversial and hotly debated concept that may have slightly different meanings. For this study, the dualistic significance of the concept of affordance is in focus.

So, interest is directed to a designed meaning on the one hand, and the affordance students discover in their meaning-making on the other. This is described as the designed and the discovered in the subheadings. Interest is directed to a comparison between what is designed and what is discovered and whether or not there is a match.

Methodology

This study aims to provide a deeper understanding into how students make meaning when working with mathematics textbooks. A comparison between the designed and the discovered is central to determining what the exercise is designed to offer and what the students actually discover. To conduct this study, different types of data were collected: textbook pages, video transcripts of students working with these pages, and the students’ representations (solutions to the exercises).

Procedure

To study students’ work with the textbook, video transcripts and representations from 18 Year 1 (ages 7–8) students were collected. The school is located in a medium-large city in the centre of Sweden and chosen from of a convenience sample. All students in the class whose caregivers had both completed the consent form participated in the study. Before the data collection, I spent a week with the class to get to know the students, so that the video recordings would not feel uncomfortable to them. Here, my former work as a compulsory-school teacher was useful; because I have twelve years of experience teaching students of this age, my participation with the students felt natural.

The aim was to study the students’ work in as natural a situation as possible, as this was a prerequisite for gaining insight into the students’ meaning-making. Of course, the most natural situation would have been to study the students in the classroom during mathematics lessons; but, since much of the work with the mathematics textbook consists of working alone in silence, that approach would not actually yield much insight into the students’ meaning-making. Gaining insight meant choosing to study the meaning-making of one student at a time in a room adjacent to the classroom. This facilitated a clearer focus on the students’ meaning-making, as I was able to ask questions to the students during their work.

The video material consists of 450 min of film – approximately 25 min per student, ranging from 19–44 min each. The videos were documented with a tablet in May 2017. A tablet was chosen because this was a device with which the students were familiar; since they used tablets in their everyday learning, it did not provoke any special attention from the students. The student and I sat at a table, with the tablet placed obliquely above us. This allowed the student, the textbook, and me to be framed in the picture. In order to influence the student as little as possible, the student started working on the exercise by herself (or himself). Then, I asked questions to understand how the student was making meaning from the exercise. This means that the questions were asked after the student had worked with the exercise. The questions were of an investigative nature, such as, “Can you tell me how you did this?”, “How did you know how to work with this page?” or “I saw that you did something with this image here, can you tell me about that?” However, if the student had difficulty getting started with the exercise, I provided support by asking questions. I chose this so the student would not feel pressured as I was there as an outside adult. This design resembles that of Rezat (2008), but as this study explores young students’ work, the section where the students highlighted and numbered their work was exchanged for a discussion together with me. To use Rezat’s design, the students need to be able to reflect on their own navigation through the exercise, which can be acknowledged as being too advanced for a 7/8-year-old student. Therefore, asking the students questions about their work with the textbook seemed more appropriate for this age.

The textbook series used in this study is well known and widely used in Sweden: Favorit matematik (Favourite Mathematics) and Mera favorit matematik (More Favourite Mathematics) (Ristola, Tapaninaho & Tirronen, 2012a, 2012b; Haapaniemi, Mörsky, Tikkanen, Vehmas, & Voima, 2013). The textbook series consists of two different tracks, of which Mera favorit matematik is described as the more challenging. Almost all chapters have a story written in the teacher’s guide that aims to bring attention to the mathematics content with associated images. The stories are about Sally the magpie, Kurre the squirrel and Isa and Charlie, two first graders.

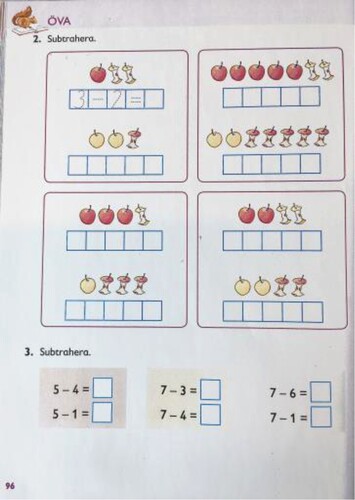
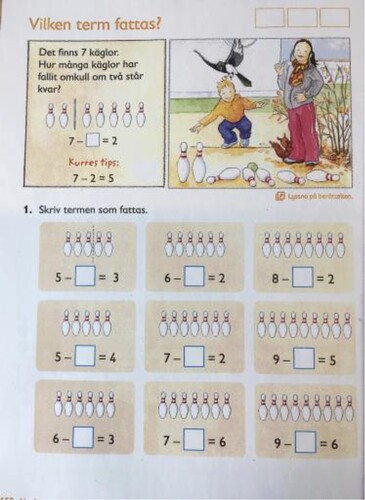
The pages were chosen on the basis of the results of a quantitative study (Norberg, 2021) using the following criteria: the exercises had to address subtraction as an arithmetic operation, be commonly used in the textbooks, and show breadth on the basis of how the different modes were used. These choices were made so as to capture different types of exercises in the chosen series of mathematics textbooks. Additionally, in order to avoid offering the students learning situations where the exercises could contain content that was mathematically new to the students and therefore could be too demanding for them, no pages from Mera favorit matematik 1B were chosen. The pages were copied in colour and given to each student one at a time and then collected for analysis. The chosen pages are shown below, with the publisher’s permission (see Figures 1–7). Exercise is defined as tasks of the same kind. For example, two exercises are pictured in Figure 1 below.

Figure 1. Exercise 1:A, 1:B.

Figure 2. Exercise 2:A.

Figure 3. Exercise 3:A.

Figure 4. Exercise 4:A, 4:B and 4:C.

Figure 5. Exercise 5:A.

Figure 6. Exercise 6:A.

Figure 7. Exercise 7:A.

Framework for analysis

To understand the students’ meaning-making, an analysis was conducted in three stages. First, a textbook analysis of the seven pages was carried out to understand the designed meanings – the designed. Next, the video data was analysed along with the students’ representations, to understand the students’ meaning-making when working with the exercises – the discovered. Finally, a comparison was made between the designed and the discovered.

Textbook analysis; the designed

The seven textbook pages were analysed to answer the question, “What are the designed meanings?” with a focus on the different modes (images, writing and mathematical symbols). This is related to the affordances that the exercises are intended to offer the students or the model reader (Eco, 1984). To obtain these answers, the teacher’s guide was studied. Where a page consisted of two or more exercises, each exercise was assigned a range. This was required on pages 1 (1:A and 1:B) and 4 (4:A, 4:B and 4:C). The following aspects were documented: the modes used, and how subtraction and central content were addressed. Additionally, the mode or modes carrying information needed to solve the exercise were documented. This provided information about which approach/approaches could be chosen to solve the exercise.

A clarification concerning the way that subtraction is addressed is necessary. Subtraction, as an arithmetic operation, can be addressed according to a specific subtraction situation or not. To document the subtraction situation, Fuson’s (1992) categorisation of subtraction was used: subtraction as change taken from (take away) and subtraction as compare. Examples of this are shown in Figure 1, where exercise A consists of a change-take-from situation, as the apples have been eaten, and exercise B is subtraction without a specific subtraction situation; the exercise does not provide any information about a specific situation, but rather about subtraction in general. Exercises offering subtraction as compare do not exist in the studied textbooks.

Video transcripts and representations; the discovered

The video transcripts were first transcribed under three separate columns in accordance with different modes: speech, images, and body language (Table 1). One column was added for whether the student solved the exercise as designed or not, and one column for comments. In the image column, the students’ use of images was documented and instances of a student drawing a picture to support her calculation. The body language column communication made with the body was documented, such as pointing, using finger-counting, shaking the head etc. The representations of the students’ answers were used as support for this analysis and placed before me while I studied the videos.

Table 1. Multimodal transcript.

Analogue textbook Year 1		Student B1
Time	Exercise	Speech	Image	Body language	Solves exercise as designed?	Ev. comment
11.30	6:A Pencils	M: How did you do? B1: First I read the text “Add and sub-tra-ct with the help of the i-ma-ge”, Although I only read to here* and then I looked here** and then I understood directly.		Using the fingers for counting under the table. B1 performs the subtraction calculations by finger-counting. here*: B1 points to the centre of the sentence in the instruction. here**: B1 points to the numbers below the images.	In part, discovers the number families in the addition calculations but not in the subtraction calculations.
13.30		M: Can you use the image when calculating? B1: Yes, you can add up all this*. But I did not think I needed to. M: Can you use the images for these ** as well? B1: Yes, I think so …  B: What?! No, you probably can’t. Because it’s 10 in total, so it’s not possible.	B1 notes that the images can be used for addition calculation but not subtraction.	this*: B1 points to the rows of pencils in the addition tasks. these**: M points to the subtraction tasks. B1 counts the pencils.

In the next step of the analysis, the focus was on whether or not the student solved the exercises as designed, both according to the subtraction content and central content. To assess whether the subtraction content was solved as designed, I used the students’ representations, their descriptions of how they solved the tasks and compared their responses with the teacher’s guides.

After that, the transcripts were coded by reading through the data several times and highlighting with colour codes, searching for the affordances the students discovered and what mode/modes guided their meaning-making, using one colour for each mode. For instance, in exercise 7:A (Figure 7, below). If the student used the image by pointing at the over-crossed dots in the images, this was coded as uses the image as a resource for calculation and image mode. If the student answered my question “How did you know how to work with this page?” with “I looked at the example and then I knew what to do.”, this was coded as uses the worked example and image, mathematical symbols and writing (as the example contained all three modes). So, students’ meaning-making as a phenomenon was of interest, together with the variation of how that phenomenon took place. The categories were thereby developed in the coding process. Then, this was summarised in a matrix (see example in Table 2 below), and the variation of the phenomenon emerged in categories and sub-categories.

Table 2. Matrix showing example of coding.

Category	Sub-category	Modes
Meaning-making based on visual support	Uses the image as a resource for calculation	Image
	Uses the image as an episode that should be interpreted	Image
	Creates one’s own visual support	Image, Body language

Quality, credibility and ethical issues

Quality is linked to credibility, confirmability, dependability and transferability (Guba & Lincoln, 1994). Credibility concerns whether the results provide a credible interpretation of the data and the extent to which the study was conducted scientifically.

The study’s confirmability concerns whether the results correspond to data. Here, my ambition was to strive for a neutral attitude throughout the research process. However, I am aware that my presence, especially when I asked questions if the student did not start their work, affected her (or his) meaning-making. Therefore, I took this into account in the analysis process. My presence affected the situation, regardless of whether I asked questions during the work with an exercise or after. Though, to gain insight into students’ working individually, this was the best solution as a pure observation would not have provided much information about how the student’s meaning-making took place, as this is an internal process. With my twelve years as a primary school teacher, I also had a pre-understanding of the phenomenon studied, bringing both advantages and disadvantages. Disadvantages can be to draw precipitant conclusions of the data. Advantages can be legitimacy in access to the field as well as long experience of communicating with students.

To achieve as high dependability as possible, I have processed the amount of data several times. Passages that seemed challenging to categorise were marked and returned. Researchers and teachers have been reference persons who have been asked for a second opinion when designing the study and during the analysis process.

Transferability refers to whether the results can be transferred to other individuals and contexts than those studied. Each student’s work with the textbook involves a unique and situated meaning-making. Even if each individual’s meaning-making is unique and is always new, the study shows examples of students’ working with mathematics textbooks in Year 1. The study shows what 18 Year 1 students’ meaning-making when working with a mathematics textbook can look like.

The participants were informed about the study’s purpose, and both caregivers gave written consent. The research followed the Swedish Research Council’s ethical codex (Vetenskapsrådet, 2017), and the empirical data has been processed accordingly.

Results

To understand students’ meaning-making when working with textbooks, it is also necessary to understand the designed meanings of the exercises and the approaches needed to solve the exercises as designed. This will be described in the first part of this section. After that, the students’ meaning-making and the approaches they used is reported and special attention is paid to when the students discover affordances other than those intended. Lastly, a short summary is given.

The designed

A summary of the designed meanings of the ten exercises is given (see also Table 3 below). To facilitate the reading, quantifications of the data are presented in summary. Here, however, I would like to emphasise that the study is not based on a quantitative approach. The quantifications are used only to overview the data.

Table 3. The designed affordances according to subtraction and central content.

Exercise	Textbook, page	Modes used	Worked example	Subtraction situation	Modes for showing subtraction situation	Central content	Modes for showing what central content is focused on	Modes for solving the exercise
1:A	Favorit-matematik 1A, 96	Image Writing Mathematical symbols	Yes, a partly solved task	Change take from	Image: apples and cores	To build number families (e.g. 6–2 = 4 and 6–4 = 2)	Image: apples and cores, boxes around tasks	Image Writing Mathematical symbols in dotted lines
1:B		Writing Mathematical symbols	No	No	–	Same as above	Image: coloured boxes	Image Writing Mathematical symbols
2:A	Favorit-matematik 1A, 150	Image Writing Mathematical symbols	Yes, a partly solved task	Change take from	Writing: “knock down”, “standing” Image: picture showing two children bowling	To work with support from images in order to calculate what term is missing	Image	Image: bowling pins and dotted line Writing Mathematical symbols
3:A	Favorit-matematik 1B, 106	Image Writing Mathematical symbols	Yes	Change take from	Image: dots crossed out	Bridging ten in subtraction, with and without image support when counting with the numbers 15–18	Image: dots crossed out Writing: “Subtract. First to ten then the rest.” Mathematical symbols: A strategy to first increase to ten shown in symbols and red lines.	Image Writing Mathematical symbols
4:A	Favorit-matematik 1B, 107	Image Writing Mathematical symbols	No	Change take from	Image: number of cookies, and indirect from page 106 which is the same spread	Same as above	Not shown in this exercise, indirect from page 106 which is the same spread	Image Writing Mathematical symbols
4:B		Writing Mathematical symbols	No	No	–	Same as above	Mathematical symbols: A strategy to first increase to ten shown in symbols Image: yellow boxes around mathematical symbols.	Writing Mathematical symbols
4:C		Writing Mathematical symbols	No	No	–	Same as above		Writing Mathematical symbols
5:A	Favorit-matematik 1B, 110	Image Writing Mathematical symbols	No	Change take from	Writing: “sell”, “left”	Practicing bridging ten in subtraction 0 to 20 Practicing strategies in problem-solving	Image: pets can be used as counters Writing: heading “Problem-solving”	Image Writing Mathematical symbols
6:A	Mera favorit-matematik 1A, 138	Image Writing Mathematical symbols	No	Change take from	Image: pencils in different colours	Repetition of addition and subtraction 0 to 10 Number families	Image: pencils in different colours. Mathematical symbols	Image Writing Mathematical symbols
7:A	Mera favorit-matematik 1A, 140	Image Writing Mathematical symbols	Yes, partly solved tasks	Change take from	Image: dots crossed out	Repetition of subtraction 0 to 10 Number families	Image: dots crossed out, boxes around tasks	Image Writing Mathematical symbols in dotted lines

Most of the studied exercises (7/10) consist of images, writing and mathematical symbols, which are also the maximum different modes that can occur in an analogue book. Exercises without images are also found (3/10). Some exercises include worked examples at the beginning of the exercise (4/10). One consists of a fully solved task while the other three consists of partly solved tasks of whom two use dotted lines for mathematical symbols.

The chosen exercises offer subtraction as change take from (Fuson, 1992) (7/10) or no subtraction situation (3/10). The three exercises that do not offer a subtraction situation are the same as the three exercises that do not consist of images, as previously mentioned. The modes providing information about the subtraction situation vary between image and writing. Image is used in five of seven exercises, image and writing in one exercise, and writing in one. Here, it could be added that mathematical symbols cannot communicate that kind of information.

The central content in the ten exercises address: subtraction 0 to 10 and number families (e.g. 6–2 = 4 and 6–4 = 2) (3/10), bridging ten in subtraction 0 to 20 (2/10), calculating what term is missing (1/10) and practising strategies in problem-solving (1/10). The modes that offer information about what central content is in focus vary between all modes; still, image mode is mainly used (9/10), writing is used in two exercises and mathematical symbols in two.

Regarding the modes used to solve the exercises, different approaches are possible. In some of the exercises, it is possible to use a combination of modes or choose one or more modes to solve the exercise. It is sometimes possible to use only mathematical symbols to do the calculation, and sometimes, image mode is also needed. In eight of ten exercises, all three modes are possible to use, and in two exercises writing, and mathematical symbols are possible choices. Altogether, different modes and approaches are required to solve the exercises and discover the central content.

The discovered

The focus now shifts to students. The students made meaning in different ways, and as mentioned earlier, it is the students’ meaning-making phenomenon and the variation of how that phenomenon took place that is studied. The data shows four different ways of making meaning when working with the ten exercises, which is to say that meaning-making is based variously on: (1) visual support, (2) mathematical symbols, (3) writing, and (4) the worked example contained in the exercise, which all will be presented in due course. One and the same student uses different approaches for different exercises when making meaning. When questions such as, “Can you tell me how you did this?” or, “How did you know how to work with this page?” were asked, the students often answered by describing the order in which they worked with the various modes in the exercise. For example, “First I looked here,” (points at the worked example) “and then here,” (points at the image) “and then I wrote the answer here” (points at the empty line where the mathematical symbols should be written). This may imply that what prompts students in the exercise governs the way they work with the exercise. It should also be stated that sometimes students changed strategy during an exercise.

The following section presents the four different approaches students used when making meaning, which are exemplified with descriptions from students’ work with various exercises. The exercises mentioned represent examples, and similar examples of meaning-making are also found in relation to exercises other than those described, but since the students’ meaning-making has a prominent position in this study, deeper descriptions linked to each individual exercise are not in focus (Norberg, 2019 does focus on these). After that, students’ meaning-making when discovering affordances other than those intended is highlighted.

Meaning-making based on visual support

One way of making meaning when working with mathematics textbooks based on visual support is to use the image. The student then starts her meaning-making with the image and represents it with mathematical symbols. The data shows two ways in which images are used: as a resource for calculation or as an episode that should be interpreted. The first way implies using the image as counters, as shown in 3:A.

The student starts with the first task in the exercise, 1a. 16–6 = __. She counts all the dots, 16, and crosses out the ones that should be subtracted, 6. Then she counts the remaining ones and writes 10 on the line.

A variation of this is to count by pointing with the finger without using the pencil to cross dots.

The second way implies interpreting what has happened, as shown in 7:A.

The student works with the exercise for a while. On the first task, for instance, he writes: “9–5 = 4”. After a time, I ask him to stop and asks: “How did you know how to work on this page?” He answers: “The crossed-out dots mean that there used to be more dots before”.

This means that the student interprets the over crossed dots as previously existed objects. Another version of making meaning based on visual support involves creating one’s own visual support. This can be done in different ways; either the student draws a picture, uses her body and counts with the fingers, or creates a number line. One example of this is in 6:A.

The student looks at the exercise. Then she draws a number line at the top of the paper and uses this for doing the calculations. I ask the student: “Is it possible to use the image?”. She frowns and says: “I don’t know.”.

This is interpreted as the student does not perceive any support in the image, so instead of counting the pencils, she creates her own number line to support the calculations. Noteworthy is that when students drew their own images, they used the margins and sometimes erased the image after using it.

Meaning-making based on mathematical symbols

Another way of making meaning when working with textbooks involves the student starting her meaning-making with the mathematical symbols. This category has three sub-categories, which will all be exemplified with data from meaning-making in 2:A. The first one consists of using mathematical symbols, and no other mode, which means that, in the meaning-making, the student focuses only on the mathematical symbols.

The student works with the exercise and writes numbers in each empty box. “How did you know how to do on this page?” I ask. He answers: “I looked at the numbers. Like here (points at the first task), 5 and 3. Then I know that it should be 2 here (points at the empty box). Because 2 and 3 is 5”. “Is it possible to use the image when doing the calculation?” I ask. “Yes.”, he answers.

This may imply that students who feel confident reading mathematical symbols actively opt out of using the images.

The second sub-category consists of starting with the mathematical symbols and then using the image, exemplified below.

The student starts his meaning-making by writing the correct mathematical symbol in the empty boxes and then draws lines to show the bowling pins to be subtracted. When I ask him if he can describe how he went along on this exercise, he says: “I counted and then I drew lines like this” (shows how to draw a line with his finger).

The third sub-category is quite similar to the second when it comes to the mathematical symbols in the empty boxes. But not when marking the pins, then the student uses the image quite arbitrarily.

After writing the correct mathematical symbol the student, randomly marks the pins. He draws a line between two pins on every task, but incorrectly. When I ask: “How did you know where to draw the lines?” He answers: “I don’t really know. I think it should be like this.”.

Here, the students meaning-making is understood as he randomly marks the pins, but without knowing what the line is supposed to illustrate. The affordances that the student discovered contained the idea that the bowling pins should be marked with a line somewhere, but not how they should be marked, which does not support the student’s mathematical learning.

Meaning-making based on writing

Students’ meaning-making can also start with the writing mode. In the data, two different ways of doing this occur. One way is to start by considering the writing mode and then use mathematical symbols. In 5:A, for instance.

The student reads the question, then performs a mental calculation and writes mathematical symbols in the boxes. When I ask how she worked with the exercise, she describes that “I read and then I calculated. And then I wrote it here (points at the line with empty boxes below the exercise)”.

The other way involves, using the image in addition to the writing and mathematical symbols when making meaning. This is exemplified in exercise 5:A by another student.

The student first reads the writing and then uses the image to count the animals to do the calculation. She points at each animal and counts loud to herself. Then she draws the mathematical symbols in the empty boxes.

Some students stated that they use the written instructions when they do not know how to work with the exercise: “I read the instructions if I don’t understand, otherwise not”. Sometimes it is not the whole instruction that is read; as a student describes, “I read to here (points at a word in the middle of the sentence), and then I understood”. The student here describes an approach where the written instruction is read only when difficulties occur and not as an approach generally used when working with the textbook.

Meaning-making based on the worked example in the exercise

There is sometimes a worked example at the beginning of the exercises, along with an instruction about how to complete the exercise. One variation of this is when the first task has an unfinished calculation in dotted lines. The data shows two different ways of making-meaning with exercises containing worked examples. One way is to start the meaning-making by reading the worked example. This is what the exercise is designed to offer, exemplified below.

After working with the exercise, I ask the student to tell me how she went along: “I looked at this (points to the first task in 1:A), and then I knew what to do.”

This means that she used the information from the worked example to solve the tasks. This is an expected approach, as this exercise’s design makes it difficult to solve the tasks on this page without using the example as a basis for the work.

Another way is to not make use of the worked example. This was shown for example according to 2:A.

When the student had worked for a while with the exercise and told me how she did, I asked her if she used the worked example, as she did not mention it in her description: “No, I don’t usually look at it so much” (giggles), she answered.

This can be interpreted as the student not viewing the worked example as important in order to solve the exercise.

When students discover affordances other than the designed

The data shows that students sometimes discover an affordance other than the designed, which can lead to a meaning-making where the designed meaning of the exercise is not discovered. This may be related to subtraction as an arithmetic operation and/or the central content. An example of this is seen in 1:A, where the designed meaning is to interpret the apples and cores as a course of an event; earlier, there were apples but no cores, but now, some of them have been eaten. Another way of interpreting the apples is shown here.

The student works with the exercise and solves the tasks incorrectly. I ask her to describe how she went along. She points at the apples and explains that “This is the first number”, and then she points at the cores and says: “And this is the other number.”.

This means that the student interprets the apples as the minuend and the cores as the subtrahend. This leads to difficulties when solving the task. For example, the task with one apple and three cores then reads: 1–3 = __.

Another example of discovering other affordances than the designed is given in 4:A, and task 1a.

The student makes an addition, where all the numbers seen in the task are added, both the ones written in the task and the number written on the cookie box. “30! Wow, I did not know that it would be that much!” she smilingly declares.

So, even if the exercise is about subtraction, the student perceives it as addition. When students discover affordances other than the designed, it is not always connected to subtraction as an arithmetic operation, but to the central content. The central content in 1:A and 1:B is to discover number families. This is indicated by coloured boxes around the pair of tasks. Another affordance given by these boxes is here described.

“I think it is to keep order”, the student answers when I asked about the boxes.

This indicates that aspects of the exercises are not always discovered by the students and that the teacher need to introduce this to the student. Another example of discovering something other than the central content is shown in 5:A. The central content is bridging ten and developing problem-solving strategies. One affordance is to give the number of squares overall importance for solving the exercise, exemplified below.

The student starts with the first task. She performs a calculation and writes down the mathematical symbols but then erases the written calculation when she realises that one box is left empty. I ask why she erases and if she believes that she calculated wrong. She answers: “I think I counted right, but there should not be empty boxes. All boxes should be used, so something is wrong. I don’t know what.”. She redoes the task, and she suddenly realises that she wrote “11” in one box instead of in two boxes. Then she is satisfied and continues with the next task.

So, it seems more important to the student to fill in all the boxes with mathematical symbols than to do a calculation that the student considers correct. These students have learned that, when this kind of exercise appears, all of the boxes should be filled in.

The last example of discovering other affordances is given when a student works with exercise 3:A.

The student draws lines between tasks that have the same answers. When I ask how he knew what to do in this exercise, he answered that the writing “draw lines” in the instructions above the tasks guided him. “It’s like an exercise where you should pair things, like a dog and a doghouse” he explains.

So, he discovers an affordance in the writing “draw lines” in the instructions above the task, instead of crossing out objects. The writing was designed to offer an instruction to cross out the right number of dots as a support for doing the calculation. This is an example of unfortunate wording.

Summary

Students’ meaning-making using visual support appears to be based on (a) the use of images or (b) the creation of one’s own visual support. Data shows that images are used in two ways: as a resource for calculation or as an episode that should be interpreted. Students also chose to draw images of their own or to use the body as visual support instead of using the images in the textbook. Concerning mathematical symbols, three different approaches are shown in the data: (a) using mathematical symbols and no other mode, (b) starting with the mathematical symbols and then using the image, or (c) starting with the mathematical symbols and then using the image quite arbitrarily. It is implied that students who feel confident reading mathematical symbols actively opt out of using the images. Meaning-making related to writing showed two different approaches: (a) to start with the writing and then use mathematical symbols, or (b) start with the writing and then use mathematical symbols together with the image. The data shows that one way students may relate to the writing is to use it when encountering obstacles, but otherwise to ignore it. Two approaches to worked examples were shown: (a) to make use of it, or (b) to not make use of it.

Conclusions and discussion

The aim of the study was to understand how students make meaning when working with mathematics textbooks. To understand this, the designed meanings of the textbook and the students’ meaning-making when working with them were studied. The results show, firstly, that the design of exercises in mathematics textbooks is complex, both in terms of how different modes are used as well as the approaches that are needed to solve the exercises as designed. Secondly, that students use different approaches when working with the textbook, from one exercise to another, as well as within the same exercise. Thirdly, that students sometimes discover affordances other than the designed, and thereby practice other content than was intended.

Students make every effort to understand, but sometimes they discover another affordance than the designed. This is shown when interpreting images, such as in 1:A, where some of the students discover the affordance that apples and cores represent the minuend and the subtrahend. Another example is when the students close gaps they discover and sometimes put a lot of energy into making meaning of peripheral aspects of the exercise. This is shown in 5:A, where mathematical symbols should be written in boxes and the student uses a lot of effort to fill every empty box with a mathematical symbol. A third example is when unfortunate wording is used, such as “draw lines” instead of “cross out”, which offered an affordance that was misleading. A final example of discovering other affordances can be found in 1:A and 7:A, in the use of boxes around tasks to show number families, which is not always discovered. These are all examples of a design that can guide students in the wrong direction. In other words, mathematics textbooks are difficult to read. This has been supported by previous research (Dyrvold, 2016; Shepherd et al., 2012) and can lead to undesirable reading strategies (Österholm, 2008). Conclusions that can be drawn from this are that textbooks could be improved and that textbook authors should be more careful in their use of images, boxes and other elements intended to guide the students, as well as their choice of wording.

Students use different approaches when working with the textbook. It may involve mainly focusing on images, mathematical symbols, writing or the worked example. These different approaches affect which meaning they make, and, by extension, the student’s mathematical learning. It is important that teachers should be aware of this. The approach that focuses mainly on mathematical symbols, for example, as also seen in Amiripour et al. (2017), can involve a risk. This is because, when starting from mathematical symbols in their meaning-making, a student can miss out on the subtraction situation the exercise was designed to offer, which may lead to a limited understanding of what subtraction as an arithmetic operation means.

Two ways of meaning-making are shown with regard to worked examples: to make use of them or not to. This result can be compared to Rezat (2008), who concluded that students rely heavily on worked examples. This implies that older students might be more likely to use worked examples than younger ones. Reasons for not using worked examples may be that students do not consider that they need them, or that they are too difficult to understand. This may imply that a greater focus on worked examples is needed during mathematics teaching.

In some of the exercises, the approach can be chosen. For example, in 3:A, it is possible to decide for oneself whether to use the images when solving the tasks. Sometimes, the approach to solve an exercise is more fixed, such as in 7:A, where the student must use the images to solve the tasks. This relates to the complexity when working with mathematics textbooks. The student must understand when different approaches can be selected and when one specific approach is needed. Therefore, students must be taught how to work with mathematics textbooks, as supported by Segerby (2017). One conclusion to draw from this is that teachers who are aware of the complexity of meaning-making when working with textbooks can plan and teach with greater insight.

Implications

All things considered; the design of exercises influences students’ meaning-making. There are considerable differences between the designed and the discovered. This is something that publishers, authors and illustrators could be made more aware of. It is not sufficient to imagine a model reader (Eco, 1984) when writing textbooks, since not all students are able to fit this description. All students working with mathematics textbooks are entitled to beneficial learning situations, and textbooks could evolve to better fit this purpose.

One implication for authors and illustrators is that more awareness is needed concerning how different modes are used in textbooks, and areas highlighted in this context are images, boxes and other elements intended to guide the students, as well as the choice of wording. Awareness that the mathematical content might not be discovered if only the mathematical symbols are used is another important area. A design where it is not possible to solve the exercise without paying attention to the mode that shows the mathematical content could be advantageous. Space for making one’s own illustrations as calculation aids could also be helpful.

An implication for teachers is that it is important to pay attention to the different modes used in the textbook and to discuss this with the students. If a student only uses the mathematical symbols in her meaning-making, it is important to find out whether the student understands the mathematical content that is in focus. With regard to images, it is of importance to communicate the approach that is needed. As for writing, it is important to be aware of the wording used. It would also be beneficial to discuss worked examples.

This study shows that mathematics textbooks are complex to read (cf. Dyrvold, 2016; Segerby, 2017) and highlights multimodal aspects of this. Additionally, the designed meaning of an exercise does not always match the student’s meaning-making. This mismatch between the designed and the discovered may deny students access to beneficial learning situations unless they receive support when working with mathematics textbooks. A greater awareness of multimodal communication is needed in order to enhance and develop mathematics teaching, and by extension, support students’ mathematical learning.

Competing interests

The author has no competing interests to declare.

Disclosure statement

No potential conflict of interest was reported by the author(s).